Лекция
Привет, Вы узнаете о том , что такое функция диссипации, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое функция диссипации, диссипативная система , настоятельно рекомендую прочитать все из категории Синергетика.
Диссипативная функция (функция рассеяния) — функция, вводимая для учета перехода энергии упорядоченного движения в энергию неупорядоченного движения, в конечном счете — в тепловую (такой переход, например, имеет место при воздействии на механическую систему сил вязкого трения).
Понятие о диссипативной функции введено в механику в 1878 г. Рэлеем, в связи с чем нередко используют развернутое ее название: диссипативная функция Рэлея .
Диссипативная функция характеризует скорость убывания (рассеяния) механической энергии системы и имеет размерность мощности. Диссипативная функция, деленная на абсолютную температуру, определяет скорость, с которой возрастает энтропия в системе (т. н. производство энтропии).
В физике
функция диссипации Рэлея , названная в честь лорда Рэлея , представляет собой функцию, используемую для обработки эффектов пропорциональных скорости сил трения в лагранжевой механике . Он определен для системы частицы как
Сила трения отрицательна градиенту скорости диссипативной функции, . Функция представляет собой половину скорости, с которой энергия рассеивается системой за счет трения.
Поскольку трение не является консервативным, оно включается в член Q j в уравнениях Лагранжа .
Диссипативная система (или диссипативная структура, от лат. dissipatio — «рассеиваю, разрушаю») — это открытая система, которая оперирует вдали от термодинамического равновесия. Иными словами, это устойчивое состояние, возникающее в неравновесной среде при условии диссипации (рассеивания) энергии, которая поступает извне. Диссипативная система иногда называется еще стационарной открытой системой или неравновесной открытой системой.
Диссипативная система характеризуется спонтанным появлением сложной, зачастую хаотичной структуры. Отличительная особенность таких систем — несохранение объема в фазовом пространстве, то есть невыполнение Теоремы Лиувилля.
Простым примером такой системы являются ячейки Бенара. В качестве более сложных примеров называются лазеры, капельный кластер, реакция Белоусова — Жаботинского, циркуляция атмосферы, процесс обучения нейронных сетей и биологическая жизнь.
Термин «диссипативная структура» введен Ильей Пригожиным.
Последние исследования в области «диссипативных структур» позволяют делать вывод о том, что процесс «самоорганизации» происходит гораздо быстрее при наличии в системе внешних и внутренних «шумов» (например, применение дропаута при обучении искусственных нейронных сетей). Таким образом, шумовые эффекты приводят к ускорению процесса «самоорганизации».
Понятие о диссипативной функции используется при изучении движения диссипативных систем, в частности — для учета влияния сопротивлений на малые колебания системы около ее положения равновесия, для исследования затухания колебаний в упругой среде, для учета тепловых потерь при затухании колебаний электрического тока в системе контуров и др. С учетом диссипации уравнения Лагранжа записываются в виде
где L — функция Лагранжа, и
— обобщенные координаты и их производные по времени, F — диссипативная функция.
В системах, внутри которых протекают физические, химические, биологические процессы, всегда производится энтропия. Об этом говорит сайт https://intellect.icu . Это производство происходит с определенной скоростью
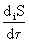 , (1)
, (1)
где нуль соответствует условию равновесия.
Производство энтропии в единицу времени diS/d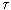 в единице объема V открытой системы обозначим буквой
в единице объема V открытой системы обозначим буквой 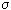 по данному определению
по данному определению
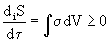 . (2)
. (2)
Величина 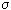 называется функцией диссипации*.
называется функцией диссипации*.
Обратим внимание на вторую принципиальную особенность введенную в рассуждения - появилось время, т. к. определяется скорость производства энтропии. Напомним, что первая принципиальная особенность состояла в возможности убывания энтропии dS<0 в открытой системе. Итак, совершен переход от термостатики, которой являлась классическая термодинамика к меняющимся во времени процессам, т.е. к динамике, к кинетике. Термостатика рассматривает равновесные процессы, т.е. протекающие очень медленно, где на каждом этапе достигается равновесие. Выше в формулах (1) и (2) совершен переход к неравновесным процессам.
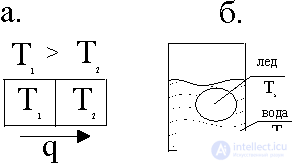
Рис. 1. Потоки тепла: а.- от первого тела ко второму; б.- при таянии льда в сосуде с водой
На рисунке рассмотрены два приведенных в соприкосновение тела при разных температурах. От более нагретого тела к менее нагретому из-за теплопроводности возникает поток теплоты, производится энтропия dS=dQ/T. Движущей силой в производстве энтропии является разность температур (T1-T2). Как будет показано ниже эту разность удобно представить в форме
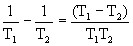 , T1>T2.
, T1>T2.
"Сконструируем" функцию диссипации в виде
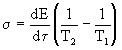 (3)
(3)
В этой формуле отражены все элементы процесса производства энтропии: поток энергии dE/d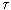 и движущая сила, создающая этот поток. В рассматриваемом случае движущей силой является разность температур. Заметим, что E является энергией, приходящейся на единицу объема [E] =Дж/м3.
и движущая сила, создающая этот поток. В рассматриваемом случае движущей силой является разность температур. Заметим, что E является энергией, приходящейся на единицу объема [E] =Дж/м3.
Рассмотрим размерности правой и левой частей формулы (3). По определению размерность функции диссипации [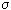 ]=
]=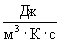 , а размерность правой части формулы (3)
, а размерность правой части формулы (3) 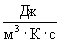 , т. е. с размерностью все в порядке.
, т. е. с размерностью все в порядке.
Можно привести второе определение функции диссипации:
Функция диссипации равна произведению потока J на силу Х, его вызывающую: 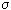 =J*Х
=J*Х
Возможно построить функцию диссипации не только для тепловых явлений.
Например, для электрических явлений потоком является сила электрического тока I, а вызывающей его силой - разность потенциалов (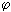 1-
1- 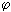 2) и
2) и 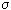
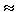 I (
I (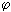 1-
1-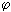 2). Электрический ток I=de/d
2). Электрический ток I=de/d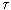 - производная заряда по времени [I(
- производная заряда по времени [I(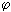 1-
1- 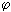 2)] =Вт=Дж/c. Из соображений размерности следует брать удельную электрическую мощность Дж/см3 и поделить ее на температуру, т. е.
2)] =Вт=Дж/c. Из соображений размерности следует брать удельную электрическую мощность Дж/см3 и поделить ее на температуру, т. е.
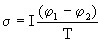 ,
,
так производится энтропия в электрических процессах.
Если в системе протекает химическая реакция, то также производится энтропия. Химическая реакция течет от большей свободной энергии к меньшей. Роль действующей силы играет разность химических потенциалов А, а потока - скорость химической реакции V, т. е. число молей вещества, испытывающих превращение в единицу времени. По указанным выше правилам "конструируем" функцию диссипации:
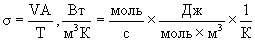
Во всех перечисленных случаях реализуются необратимые процессы. Выше функция диссипации 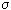 везде была представлена как произведение потока J на силу X, его вызывающую.
везде была представлена как произведение потока J на силу X, его вызывающую.
Читателю рекомендуется так же ознакомтся с параграфом Сопряженные процессы в открытых системах и примерами к главе Термодинамика открытых систем и живые организмы
В заключение отметим, что в этом разделе кратко изложены работы основателей термодинамики необратимых процессов Л. Онзагера, Де Донде и И. Пригожина, которые в 1977 г. за работы по термодинамике необратимых процессов и их использование в химии и биологии были удостоены Нобелевской премии.
И. Пригожин (1917) - бельгийский физик, член Бельгийской АН, директор Международного института физики и химии (Бельгия), член АН СССР, ввел понятия производство энтропии и поток энтропии, дал локальную формулировку второго начала ТД, сформулировал теорему Пригожина, автор многих монографий по неравновесной термодинамике.
Л. Онзагер (1903 - 1976) - американский химик и физик, профессор химии ряда американских университетов. В 1931 г. доказал ряд теорем термодинамики необратимых процесaсов.
Диссипативными называют системы, обладающие свойством сжатия фазового объема, которое иллюстрирует рис.2. На нем представлено множество начальных точек, занимающее объем 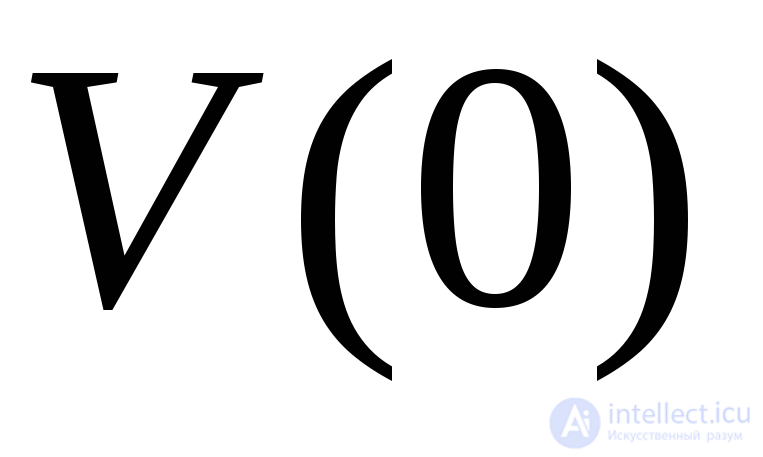 , стартуя из которого, система через времяt оказывается в точках, образующих множество объема
, стартуя из которого, система через времяt оказывается в точках, образующих множество объема 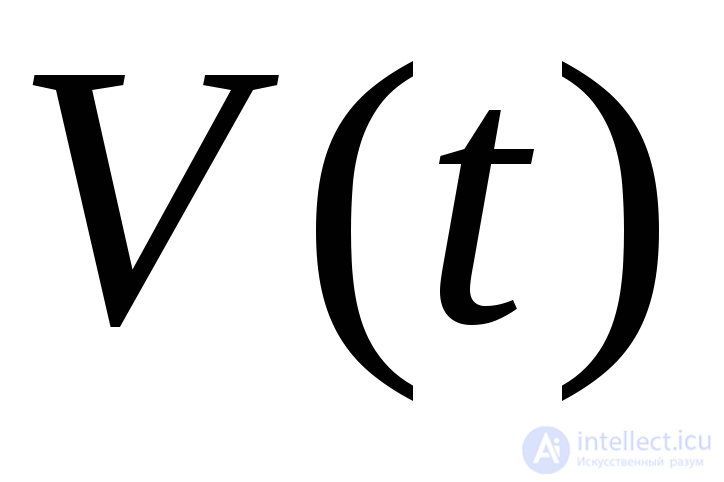 . Система диссипативна, еслиc течением времени фазовый объем уменьшается
. Система диссипативна, еслиc течением времени фазовый объем уменьшается 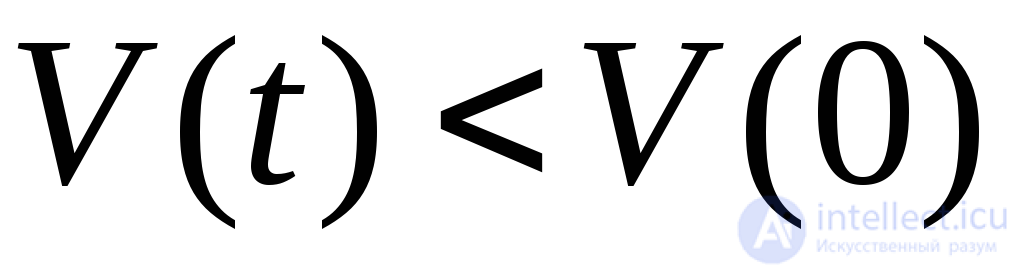 . В одномерном случае мерой фазового объемаV является длина, в двухмерном – площадь, в многомерном (
. В одномерном случае мерой фазового объемаV является длина, в двухмерном – площадь, в многомерном (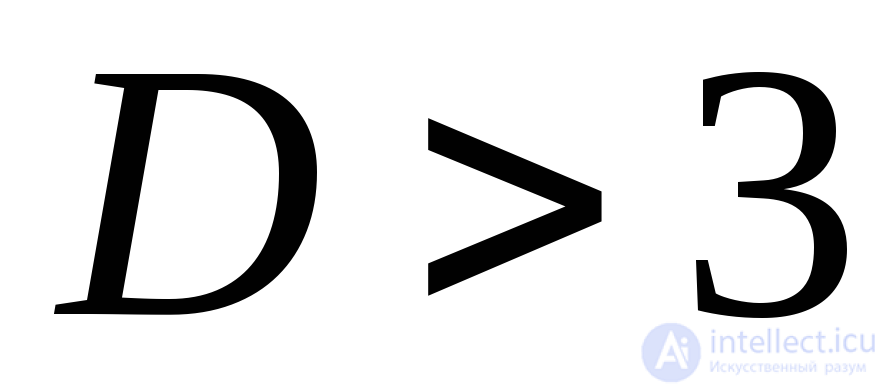 ) – гиперобъем. В конце концов, изображающие точки из стартового объема попадают на аттракторы, объем которых равен 0. Представленное определение диссипативной системы является более широким, чем определение диссипативной системы, используемое в физике, где это – система с трением, в которой механическая (более упорядоченная) энергия переходит в энергию хаотического движения молекул. Вконсервативных системах (в физике это – системы без трения) начальный фазовый объем сохраняется, но может изменить свою форму (рис.2,б).
) – гиперобъем. В конце концов, изображающие точки из стартового объема попадают на аттракторы, объем которых равен 0. Представленное определение диссипативной системы является более широким, чем определение диссипативной системы, используемое в физике, где это – система с трением, в которой механическая (более упорядоченная) энергия переходит в энергию хаотического движения молекул. Вконсервативных системах (в физике это – системы без трения) начальный фазовый объем сохраняется, но может изменить свою форму (рис.2,б).
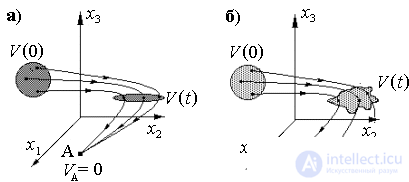
Рис.2. Иллюстрация некоторых вариантов деформации фазового объема: а) диссипативная система, б) консервативная система. Линии – фазовые траектории
Совокупность характерных фазовых траекторий называют фазовым портретом системы. При определенном навыке по фазовому портрету можно многое сказать о возможных движениях системы. Заметим, что в самой фазовой траектории (кривой в фазовом пространстве) информация о моменте времени, когда точка оказывается в том или ином ее месте, отсутствует. Для иллюстрации рассмотрим элементы фазового портрета системы:
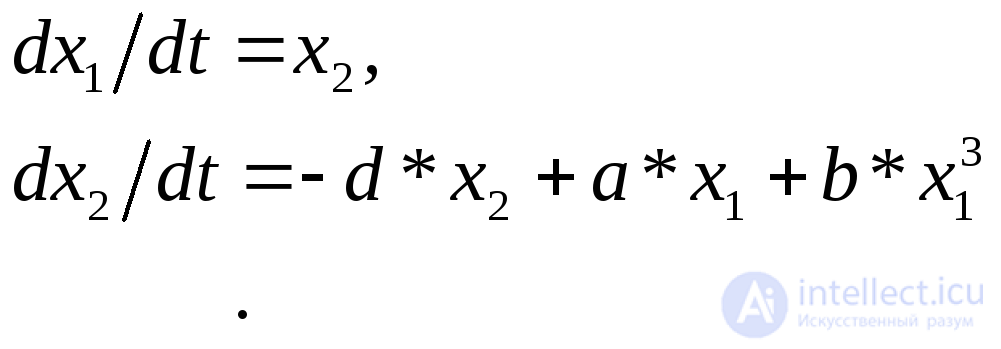 (3),
(3),
которая моделирует, в частности, колебания в потенциальной яме с двумя минимумами при наличии трения, подобно показанному на рис.3,а шарику, катающемуся в двухъямном профиле. Линии на фазовой плоскости 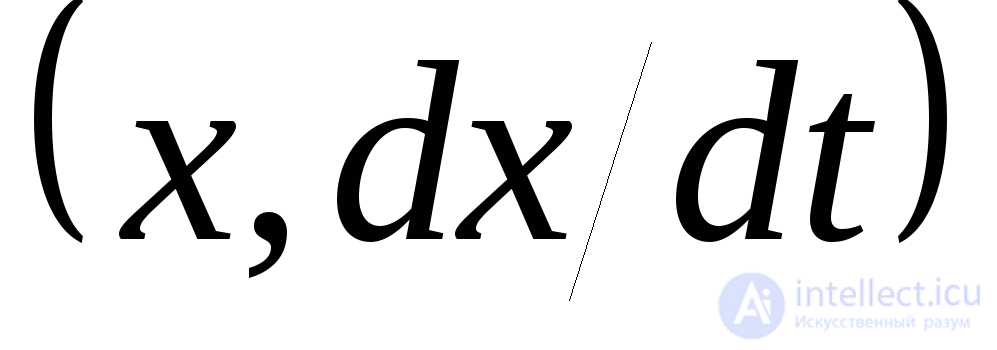 (рис.3б) – фазовые траектории, выходящие из точек 1 и 2. Они не могут пересекаться, т.к. последнее означало бы нарушение правила динамического описания – у одного настоящего одно будущее! Ситуации, похожие на пересечения, возможны вособых точках – точках равновесия, в которых состояние динамической системы остается неизменным сколь угодно долго. Таких точек на портрете три:
(рис.3б) – фазовые траектории, выходящие из точек 1 и 2. Они не могут пересекаться, т.к. последнее означало бы нарушение правила динамического описания – у одного настоящего одно будущее! Ситуации, похожие на пересечения, возможны вособых точках – точках равновесия, в которых состояние динамической системы остается неизменным сколь угодно долго. Таких точек на портрете три: 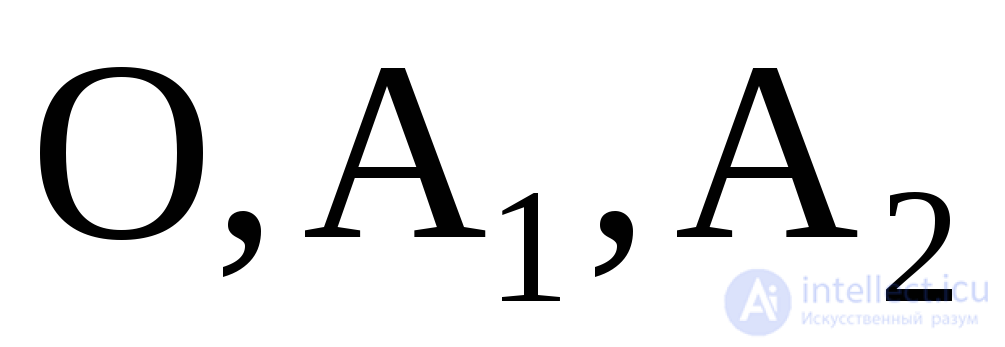 . Первая соответствует положению покоящегося шарика на вершине горки (рис.3а), а вторые – в левой и правой ямках. Большинство других точек фазового пространства соответствуют состояниям, в которых изображающие точки в следующий момент не остаются. Их движению в фазовом пространстве соответствует тот или иной вид фазовой траектории и зависимости динамических переменных от времени
. Первая соответствует положению покоящегося шарика на вершине горки (рис.3а), а вторые – в левой и правой ямках. Большинство других точек фазового пространства соответствуют состояниям, в которых изображающие точки в следующий момент не остаются. Их движению в фазовом пространстве соответствует тот или иной вид фазовой траектории и зависимости динамических переменных от времени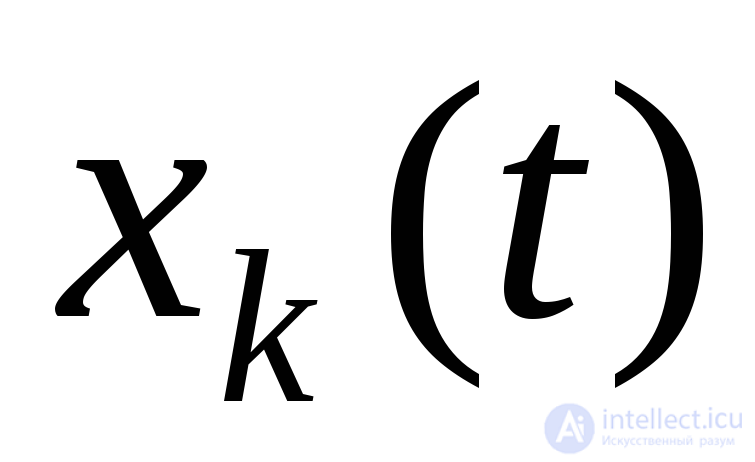 , рис.3б. Обратите внимание, что в типичной фазовой траектории можно выделить начальный участок (переходный процесс) и более поздний этап движений, которые отличаются большей степенью повторяемости – установившиеся движения.
, рис.3б. Обратите внимание, что в типичной фазовой траектории можно выделить начальный участок (переходный процесс) и более поздний этап движений, которые отличаются большей степенью повторяемости – установившиеся движения.
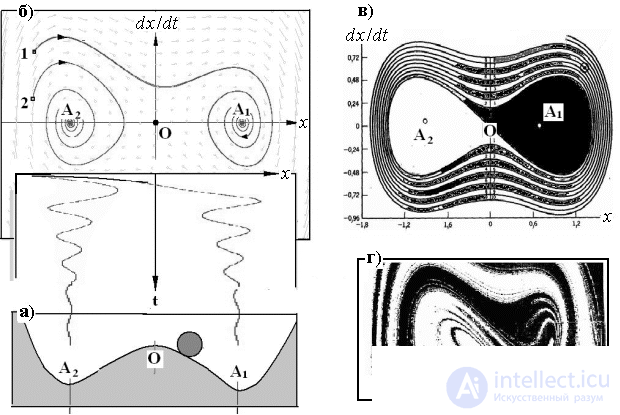
+Рис.3. Шарик в двойной ямке (а); его фазовый портрет и временные реализации колебаний (б); бассейны притяжения аттракторов (точек равновесия 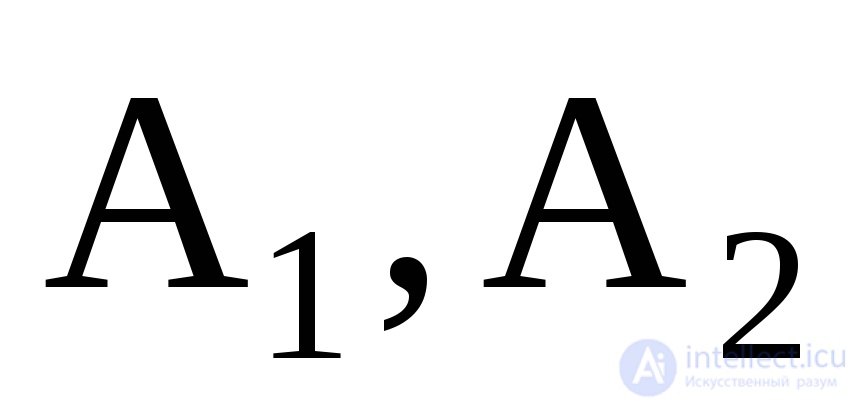 ), сосуществующих в фазовом пространстве (в); бассейны притяжения неавтономной системы при значениях параметров, когда в фазовом пространстве сосуществуют два хаотических аттрактора (г)
), сосуществующих в фазовом пространстве (в); бассейны притяжения неавтономной системы при значениях параметров, когда в фазовом пространстве сосуществуют два хаотических аттрактора (г)
Прочтение данной статьи про функция диссипации позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое функция диссипации, диссипативная система и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Синергетика
Комментарии
Оставить комментарий
Синергетика
Термины: Синергетика