Лекция
Привет, Вы узнаете о том , что такое информация мера информации по шеннону, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое информация мера информации по шеннону , настоятельно рекомендую прочитать все из категории Синергетика.
Приводится определение информации по Шеннону и методы ее оценки, пришедшие из теории вероятностей. Рассматривается на конкретном примере оценка информации в тексте. Вводятся определения избыточности информации, коэффициента стохастичности, оптимального соотношения между детерминированностью и стохастичностью. Демонстрируется применение коэффициента стохастичности к анализу различных явлений в архитектуре городов, произведениях искусства и социальной жизни. Анализируется информационная мера упорядоченности, гармония и хаос в природе.
I. Качество информации, имеющейся о системе может быть оценено количественно на основании формулы Шеннона для информационной энтропии, а также выражений для избыточности информации и коэффициента стохастичности.
II. Существуют различные взгляды на понятие информации и ее ценности. Соотношение гармонии и хаоса в системе поддается количественному анализу и может быть исследовано на оптимальность.
В разделе 2.4 была приведена знаменитая формула Больцмана, определяющая связь энтропии со статистическим весом P системы
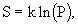 (1)
(1)В середине XX века (1948 г.) была создана теория информации, с появлением которой введенная Больцманом функция (1) пережила второе рождение. Американский инженер-связист Клод Шеннон предложил ввести меру количества информации с помощью статистической формулы энтропии.
Заметим, что понятие "информация" обычно трактуется как "сведения", а передача информации осуществляется с помощью связи. Об этом говорит сайт https://intellect.icu . Связь между количеством информации и энтропией послужила ключом к решению ряда научных проблем.
Приведем ряд примеров. При бросании монеты выпадает орел или решка, это определенная информация о результатах бросания. При бросании кости получаем информацию о выпадении определенного количества очков (например, трех). В каком случае мы получаем больше информации?
Вероятность W выпадения герба равна 1/2, вероятность выпадения трех очков - W=1/6. Реализация менее вероятного события дает больше информации: чем больше неопределенность до получения сообщения о событии (бросание монеты, кости), тем большее количество информации поступает при получении сообщения. Информация I связана с числом равновероятных возможностей P - для монеты P=2, для кости P=6. При бросании двух костей получаем вдвое больше информации, чем при бросании одной кости: информация независимых сообщений аддитивна, а числа равновероятных возможностей перемножаются. Значит, если имеются два набора равновероятных событий P1 и P2 , то полное число событий
а количество информации I складывается, т. е.
Известно, что правилам (2) и (3) подчиняются логарифмические функции, т. е. зависимость количества информации I от числа равновероятных событий должна иметь вид
где постоянная А и основание логарифма могут быть выбраны по соглашению. В теории информации условились полагать А=1, а основание логарифма двум, т. е.
При бросании монеты получается информация (Р=2), которую примем за единицу информации I=1:
Бит - двоичная единица информации (binary digits), она оперирует двумя возможностями: да или нет, числа в двоичной системе записываются последовательностью нулей и единиц.
В общем виде (вывод) формула (4) принимает вид:
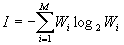 . (5)
. (5)Величина (5) названа Шенноном информационной энтропией.
Такой подход к количественному выражению информации далеко не универсален, т. к. принятые единицы не учитывают таких важных свойств информации, как ее ценность и смысл. Абстрагирование от конкретных свойств информации (смысл, ценность ее) о реальных объектах, как в дальнейшем выяснилось, позволило выявить общие закономерности информации. Предложенные Шенноном для измерения количества информации единицы (биты) пригодны для оценки любых сообщений (рождение сына, результаты спортивного матча и т. д.). В дальнейшем делались попытки найти такие меры количества информации, которые учитывали бы ее ценность и смысл. Однако тут же терялась универсальность: для разных процессов различны критерии ценности и смысла. Кроме того, определения смысла и ценности информации субъективны, а предложенная Шенноном мера информации объективна. Например, запах несет огромное количество информации для животного, но неуловим для человека. Ухо человека не воспринимает ультразвуковые сигналы, но они несут много сведений для дельфина и т. д. Поэтому предложенная Шенноном мера информации пригодна для исследования всех видов информационных процессов, независимо от "вкусов" потребителя информации.
Прочтение данной статьи про информация мера информации по шеннону позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое информация мера информации по шеннону и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Синергетика
Из статьи мы узнали кратко, но содержательно про информация мера информации по шеннону
Комментарии
Оставить комментарий
Синергетика
Термины: Синергетика