Лекция
Привет, Вы узнаете о том , что такое ма тическая модель лазера , Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое ма тическая модель лазера , настоятельно рекомендую прочитать все из категории Синергетика.
Как указывалось ранее, в лазере в процессе стимулированного излучения порождаются фотоны: возбуждая атомы, мы создаем инверсию заселенности и при возвращении атома в нормальное состояние излучается свет единой фазы и частоты, т. е. происходит когерентное излучение. Если активные атомы накачиваются (возбуждаются) внешними источниками слабо, лазер действует как обычная лампа. Атомы независимо друг от друга испускают волновые цуги со случайными фазами и рассматриваются как осциллирующие диполи, колеблющиеся случайным образом. Если увеличивать накачку, то внезапно, при очень малом изменении накачки лазер переходит в новое, высокоорганизованное состояние. Атомные диполи теперь осциллируют в фазе, хотя и возбуждаются накачкой случайным образом. Таким образом, в атомной системе проявляется самоорганизация. Высокая когерентность лазерного излучения вызвана кооперативным поведением атомных диполей, т. е. Взаимосодействием.
Скорость порождения фотонов, или изменения со временем числа фотонов dn/d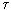 =
= определяется уравнением вида
определяется уравнением вида
 = Прирост - Потери (1)
= Прирост - Потери (1)Прирост вызван стимулированным излучением и пропорционален числу уже имеющихся фотонов n и числу возбужденных атомов N, т. е.
Потери обусловлены уходом фотонов через торцы лазера. Допустим, что скорость ухода пропорциональна числу имеющихся фотонов, т. е.
 n, 2
n, 2 = 1/
= 1/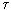 0, (3)
0, (3)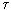 0 - время жизни фотона в лазере.
0 - время жизни фотона в лазере.
Число возбужденных атомов N уменьшается за счет испускания фотонов, т. Об этом говорит сайт https://intellect.icu . е. N(n), и уравнение (1) становится нелинейным. Если в отсутствие лазерной генерации число возбужденных атомов поддерживается внешней накачкой на постоянном уровне N0, то из-за генерации истинное число возбужденных атомов будет меньшим на величину  N. Это уменьшение
N. Это уменьшение  N пропорционально числу имеющихся в лазере фотонов n, т. к. эти фотоны постоянно заставляют атомы возвращаться в основное состояние; таким образом
N пропорционально числу имеющихся в лазере фотонов n, т. к. эти фотоны постоянно заставляют атомы возвращаться в основное состояние; таким образом
 N,
N,  N =
N =  n. (4)
n. (4)Подставляя (1) и (2) в (4), получаем основное уравнение упрощенной лазерной модели
 =-kn-k1n2, k = 2
=-kn-k1n2, k = 2 - GN0 (5)
- GN0 (5)Если число возбужденных атомов N0 невелико, то k положительно, а при больших N0 коэффициент k может стать отрицательным; изменение знака происходит при
 (6)
(6)Это условие порога лазерной генерации. Известно, что при k > 0 лазерной генерации нет, а при k < 0 возникает лазерная генерация.
Решение дифференциального уравнения (5) имеет вид
 , (7)
, (7) .
.Здесь n0=n(0) - начальное состояние.
Временное поведение функции (7) таково, что она приближается к стационарному состоянию n=0 или n =|k/k1| независимо от начального значения n0, но в зависимости от знаков k, k1.
В двухмодовом лазере порождаются фотоны двух типов 1 и 2 в количестве n1 и n2. По аналогии с (5), (6) скоростные уравнения имеют вид
 |
 |
 |
 1n1 -
1n1 - 2n2
2n2Условие стационарности
 1=
1= 2
2
Прочтение данной статьи про ма тическая модель лазера позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое ма тическая модель лазера и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Синергетика
Из статьи мы узнали кратко, но содержательно про ма тическая модель лазера
Комментарии
Оставить комментарий
Синергетика
Термины: Синергетика