Лекция
Привет, Вы узнаете о том , что такое частицы в магнитном поле, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое частицы в магнитном поле , настоятельно рекомендую прочитать все из категории Переменный электрический ток. Электромагнитное поле.
Еще в глубокой древности было известно, что некоторые минералы, например магнитный железняк (химический состав
31 % — Fe, 69 % — O), способны притягиваться друг к другу, а также притягивать к себе кусочки железа. Такие тела называются магнитами. Наибольшей силой притяжения обладают противоположные концы магнита, которые называются магнитными полюсами.
Знания античного мира о магнитах были минимальны. Практическое применение магниты нашли в средневековье, когда появился исключительно важный прибор — компас. Изобретатель его неизвестен. Бытовало мнение, что компас, давным-давно изобретенный в Китае, был завезен в Европу Марко Поло (1254–1324). Однако есть письменные европейские источники XII в., где уже описывается употребление компаса, а его изобретение приписано арабам. В некоторых китайских источниках примерно того же времени изобретение компаса приписывается неведомым иноземным мореходам. Как бы то ни было, магнитная стрелка, помещенная на острие и способная свободно вращаться вокруг вертикальной оси, позволила совершить множество географических открытий.
Магнитная стрелка в каждой точке поверхности Земли (при отсутствии помех) принимает строго определенное направление: одним концом она приблизительно указывает в направлении геофизического севера, а другим — на юг. Конец магнитной стрелки, который указывает на север, условно называется северным (N), а противоположный — южным (S) (рис. 5.1).
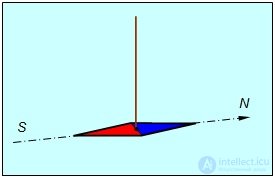
Рис. 5.1. Поведение магнитной стрелки в магнитном поле Земли
Если в некоторой области пространства на магнитную стрелку действуют силы, стремящиеся установить ее в определенном направлении, то мы говорим, что там имеется магнитное поле. Поведение стрелки компаса в магнитном поле (Земли или любого другого источника) позволяет ввести линии магнитной индукции (силовые линии магнитного поля) по аналогии с силовыми линиями электрического поля. В каком-то смысле это даже легче: стрелка сама указывает направление силовой линии в точке, где она находится. Основной cиловой характеристикой магнитного поля является вектор магнитной индукции В. направленный по касательной к силовой линии, проходящей через данную точку. В различных точках поля индукция по величине и направлению имеет различные значения.
На рис. 5.2 демонстрируется ориентация магнитной стрелки, которая может вращаться вокруг горизонтальной и вертикальной осей, вдоль вектора индукции магнитного поля Земли, наклоненного под некоторым углом к горизонту.
Рис. 5.2. Ориентация магнитной стрелки в магнитном поле Земли
На рис. 5.3 показано, что катушка с током в магнитном поле земли ведет себя аналогично магнитной стрелке. Ось длинной катушки с током, подвешенной на тонкой нити в горизонтальном положении, ориентируется вдоль горизонтальной составляющей вектора магнитной индукции магнитного поля Земли, то есть в направлении север-юг, как и обычная магнитная стрелка.
Рис. 5.3. Ориентация длинной катушки с током в магнитном поле Земли
Линии магнитной индукции, в отличие от линий электростатического поля, всегда замкнуты. Если говорить о магнитном поле постоянных магнитов, то принято считать, что линии выходят из северного полюса магнита, входят в южный и замыкаются внутри магнита (рис. 5.4)
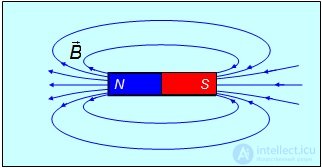
Рис. 5.4. Силовые линии постоянного магнита
На основании опыта установлено, что разноименные полюса притягиваются, одноименные отталкиваются. В этом смысле взаимодействие магнитов похоже на взаимодействие заряженных тел. Поведение стрелки компаса означает, что существует земной магнетизм, подобно тому, как существует гравитационное поле Земли, обусловленное ее массой. Поскольку обращаемый к северу конец стрелки назвали северным полюсом, а притягиваются разноименные полюса, то вблизи северного географического полюса Земли находится южный магнитный. Иными словами, магнитное поле Земли имеет направление с юга на север (рис. 5.5).
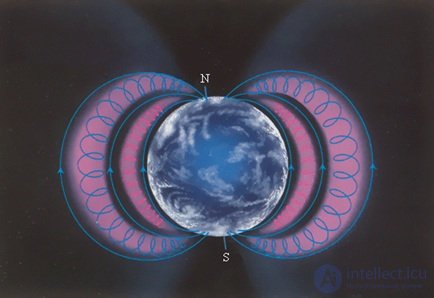
Рис. 5.5. Магнитное поле Земли: северный магнитный полюс N находится вблизи южного географического
Показаны радиационные пояса Земли — внутренний (протонный) и внешний (электронный), —
где благодаря магнитному полю задерживаются заряженные частицы космических лучей
Электростатическое поле Е порождается электрическими зарядами и воздействует на них, что символически изобразим как
Два полюса магнита наводят на мысль о симметричном соотношении
Оказалось, однако, что симметрия между магнитными и электрическими явлениями не столь прямолинейна. Если отдельные тела можно зарядить либо только положительно, либо только отрицательно, поскольку существуют элементарные заряженные частицы — носители электрических зарядов разных видов, — то отделить один из магнитных полюсов от противоположного невозможно. Если разрезать на две части магнит, то каждая часть будет снова вести себя как самостоятельный магнит, имеющий на своих концах противоположные полюсы (рис. 5.6).
Рис. 5.6. При попытке разделить магнит на два разноименных магнитных заряда (монополя)
оказывается, что каждая из частей по-прежнему обладает двумя полюсами
Что произойдет, если при делении дойти до того, что разбить магнит на отдельные атомы? Можно ли тогда отделить северный полюс от южного? Нет, даже отдельные атомы ведут себя как микроскопические, но тем не менее «полноценные» магниты с северным и южным полюсами. Оказывается, что даже отдельные элементарные частицы (например, электроны) представляют собой микромагниты. В настоящее время отсутствуют какие-либо экспериментальные доказательства того, что в природе могут существовать отдельные магнитные заряды (монополи), подобные электрическим. Оказалось, что магнитное поле порождается движущимися электрическими зарядами и, в свою очередь, оказывает воздействие на них, так что наша схема принимает вид
|
|
(5.1) |
В быту мы обычно имеем дело с малыми электрическими зарядами. В то же время заряд, протекающий через поперечное сечение проводника даже при небольшом токе, велик из-за огромной концентрации электронов в металле. Поэтому неудивительно, что первые экспериментальные наблюдения связи электрических и магнитных явлений были реализованы по схеме
|
|
(5.2) |
Если понимать под стрелками в (5.2) экспериментальное подтверждение указанной связи, то первую из них (порождение магнитного поля током) провел датский ученый Г.X. Эрстед.
В 1820 г. Эрстедом было экспериментально установлено, что проводники, по которым текут токи, также взаимодействуют с магнитной стрелкой. Схема опыта Эрстеда показана на рис. 5.7. Около неподвижного провода, расположенного вдоль меридиана, располагается магнитная стрелка, которая при выключенном токе располагается параллельно проводу. При включении тока магнитная стрелка поворачивается, стремясь установиться перпендикулярно проводу.
Рис. 5.7. Опыт Эрстеда:
1 — схема опыта; 2 — положение стрелки при выключенном токе; 3 — положение стрелки при включенном токе
Положение магнитной стрелки, помещенной около проводника с током, изменяется с изменением направления тока, но стрелка совершенно не реагирует на неподвижные электрические заряды. Отсюда можно сделать вывод, что способностью создавать магнитное поле обладают лишь движущиеся электрические заряды (электрический ток), а вокруг неподвижных зарядов существует только электростатическое поле. Магнитное поле, возникающее в пространстве около проводников с током, как и электрическое поле, обусловленное неподвижными зарядами, является одним из видов материи. Как мы вскоре увидим, оно обладает определенными физическими свойствами и характеризуется энергией.
Вторая стрелка в нашей схеме (5.2) — действие магнитного поля на ток была реализована в том же 1820 г. в экспериментах Ж. Био, Ф. Савара и А. Ампера. Поскольку ток есть движение большого числа элементарных зарядов, естественно рассмотреть наиболее простую систему — один движущийся заряд.
Сила, с которой магнитное поле действует на движущийся со скоростью v заряд q, пропорциональна величине магнитного поля, то есть вектору магнитной индукции B, скорости заряда v, величине самого заряда q. Эксперименты показали, что эта сила ортогональна как скорости заряда, так и вектору магнитной индукции. Эта сила называется силой Лоренца, и определяется она векторным произведением
|
|
(5.3) |
Согласно этому выражению, сила Лоренца перпендикулярна плоскости, где расположены векторы v и B и определяется для положительного заряда по правилу винта (рис. 5.8).
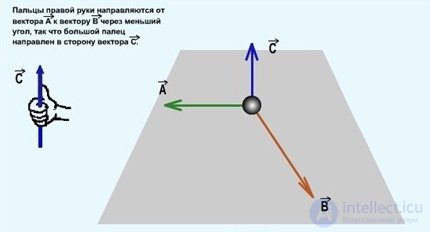
Рис. 5.8. Правило винта для определения направления векторного произведения
Модуль силы Лоренца равен
|
|
(5.4) |
где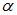 
— угол между векторами v и B. Приведенные соотношения можно использовать для измерения величины и направления вектора магнитной индукции B, так же как соотношение
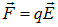
Является, определением вектора напряженности электрического поля.
|
В системе СИ единицей измерения магнитной индукции является тесла (Тл)
|
Тесла — большая величина, магниты с полем 10–8 Тл относятся к рекордным.
Поскольку сила Лоренца FL всегда направлена перпендикулярно к скорости движения частицы v, она не совершает работы. Следовательно, кинетическая энергия заряженной частицы при движении в магнитном поле не изменяется, а значит, не меняется величина скорости частицы. Сила Лоренца изменяет лишь направление вектора v, то есть сообщает частице нормальное ускорение.
Если заряд движется в области, где существует и электрическое поле E, и магнитное поле B, то на него действует полная сила
|
|
(5.5) |
(Часто эту полную силу, действующую на заряд в электромагнитном поле, и называют силой Лоренца).
Движение заряженных частиц в электрических и магнитных полях лежит в основе многих явлений, происходящих во Вселенной. Так, например, заряженные частицы космических лучей, взаимодействуя с магнитным полем Земли, вызывают много интересных явлений, в том числе полярные сияния. Земное магнитное поле способно захватывать заряженные частицы, попадающие из космоса в окрестность Земли, в результате чего и возникли окружающие Землю радиационные полюса (см. рис. 5.5).
Изучение движения заряженных частиц в электрических и магнитных полях сделало возможным определение удельных зарядов этих частиц (то есть отношений заряда к их массе) и отсюда получать ценные сведения о природе частиц и о тех процессах, в которых они возникают.
Воздействие на потоки электронов и других заряженных частиц электрических и магнитных полей используется для управления этими потоками, что лежит в основе различных физических приборов от электронно-лучевых трубок до самых современных ускорителей заряженных частиц.
На рис. 5.9 показан опыт, демонстрирующий отклонение пучка электронов в электронно-лучевой трубке (рис. 5.10) под действием силы Лоренца, возникающей при приближении к трубке постоянного магнита, имеющего форму длинного цилиндра. Показывается, что сила перпендикулярна направлению тока в пучке и направлению магнитного поля и меняет знак при изменении направления магнитного поля.
Рис. 5.9. Отклонение пучка электронов в электронно-лучевой трубке под действием силы Лоренца
Рис. 5.10. Электронно- лучевая трубка с отклоняющими пластинами и катушками
На рис. 5.11 представлен опыт Де ля Риво, где наблюдается воздействие магнитного поля на дуговой разряд в разреженном газе. Газ находится в колбе, в которую введен цилиндрический конец сердечника электромагнита. Разряд происходит между электродом наверху колбы и кольцом внизу, охватывающим сердечник. После включения магнитного поля шнур разряда между верхним электродом и кольцом под действием силы Лоренца начинает вращаться вокруг сердечника, причем при изменении направления магнитного поля меняется и направление вращения шнура.
Рис. 5.11. Опыт Де ля Риво
Примеры магнитных полей, встречающихся в нашем мире, приведены на рис. 5.12.
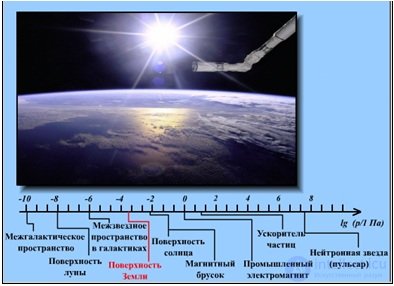
Рис. 5.12. Характерные магнитные поля в природе
Если начальная скорость заряженной частицы v перпендикулярна магнитному полю В, то в этом случае частица под действием силы Лоренца будет двигаться по окружности постоянного радиуса R (рис. 5.13)
|
|
(5.6) |
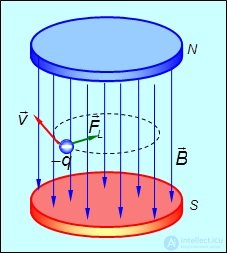
Рис. 5.13. Движение отрицательно заряженной частицы в однородном магнитном поле
Сила Лоренца FL, направленная по радиусу к центру окружности, вызывает радиальное ускорение. По второму закону Ньютона имеем
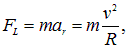
следовательно, можем записать уравнение
|
|
(5.7) |
из которого легко получить выражение для угловой скорости частицы
|
|
(5.8) |
Если q, m и B — постоянные величины, то угловая скорость, а следовательно, и период
|
|
(5.9) |
тоже являются постоянными величинами, не зависящими от энергии частицы. От скорости движения частицы зависит только радиус орбиты
|
|
(5.10) |
Сила Лоренца создает только нормальное ускорение и, соответственно, направлена к центру окружности. Следовательно, направление вращения положительно заряженной частицы таково, что вращающийся в том же направлении винт будет двигаться против направления поля. Об этом говорит сайт https://intellect.icu . Отрицательно заряженная частица вращается в противоположном направлении (см. рис. 5.14, 5.15).
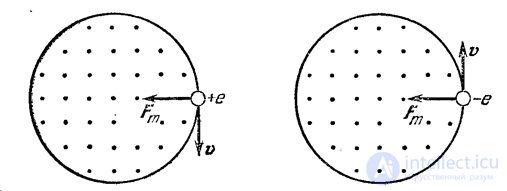
Рис. 5.14. Движение положительно и отрицательно заряженных частиц в однородном магнитном поле.
Направление магнитного поля указано точками
Если начальная скорость частицы параллельна вектору магнитной индукции, то сила Лоренца равна нулю. Частица будет продолжать двигаться в том же направлении прямолинейно и равномерно.
Наконец, в общем случае можно представить себе, что частица влетает в область однородного магнитного поля со скоростью v, составляющей угол q с направлением магнитного поля. Эту скорость можно разложить на компоненту две составляющих, одна из которых
направлена вдоль поля, а вторая
перпендикулярна полю. Соответственно, движение частицы является суммой двух движений: равномерного вдоль поля со скоростью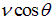 
и вращения по окружности с угловой скоростью 
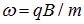. Траектория частицы, таким образом, является спиралью с радиусом R и шагом h (рис. 5.15):
|
|
(5.11) |
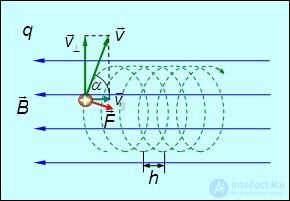
Рис. 5.15. Движение заряженной частицы по спирали в однородном магнитном поле
Пример. В однородном магнитном поле с индукцией 2 Тл движется протон. Траектория его движения представляет собой винтовую линию с радиусом 10 см и шагом 60 см. Определить скорость и кинетическую энергию протона. Какую ускоряющую разность потенциалов U прошел протон перед тем, как влететь в магнитное поле?
Решение. Из уравнений (5.11) находим угол между скоростью протона и полем
|
|
(5.12) |
откуда
|
|
(5.13) |
Кинетическая энергия протона будет
|
|
(5.14) |
Мы могли использовать нерелятивистскую формулу для энергии, так как скорость протона много меньше скорости света.
Если протон ускорялся электрическим полем, то при прохождении разности потенциалов U он приобрел энергию eU. Отсюда находим разность потенциалов
|
|
(5.15) |
Джоуль — слишком большая энергия в мире элементарных частиц. Здесь используют внесистемную единицу — электронвольт (эВ).
|
Электрон-вольт (эВ) — это внесистемная единица энергии, численно равная энергии, которую приобретает электрон, пройдя ускоряющую разность потенциалов 1 В
|
Она удобна тем, что любая другая частица с зарядом по модулю равным заряду электрона, ускоренная разностью потенциалов в 3,66 МэВ, как в нашем примере, имеет кинетическую энергию 3,66 МэВ (мегаэлектронвольт).
Циклотрон
Независимость периода обращения нерелятивистской заряженной частицы в однородном магнитном поле от ее скорости положена в основу ускорителя заряженных частиц, называемого циклотроном. В циклотроне заряженная частица, помещенная между полюсами электромагнита, многократно проходит через электрическое поле, каждый раз увеличивая свою энергию на величину от нескольких сотен до нескольких тысяч электронвольт. С увеличением скорости частицы (с ростом ее энергии) радиус орбиты увеличивается, поэтому частица в циклотроне будет двигаться по спирали. Циклотрон состоит из двух электродов в виде половинок круглой невысокой коробки (рис. 5.16).
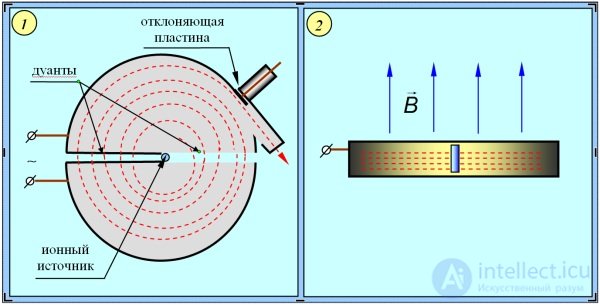
Рис. 5.16. Схема циклотрона: 1 — вид сверху; 2 — вид сбоку
Электроды называются дуантами из-за сходства их формы с заглавной латинской буквой D. Дуанты заключены в откачиваемый корпус (вакуум 10–5 мм рт. ст.), который помещен между полюсами большого электромагнита. Поле, создаваемое электромагнитом, однородно и перпендикулярно к плоскости дуантов. На дуанты подается переменное напряжение, создаваемое высокочастотным генератором. Вблизи центра магнита в промежутке между дуантами располагается источник заряженных частиц — ионов. Положительный ион, вылетающий из источника в то время, когда электрод 2 имеет отрицательный потенциал, приобретает некоторую скорость и в внутри дуанта 2 опишет полуокружность постоянного радиуса, так как внутри дуанта электрическое поле отсутствует, но есть магнитное поле. К моменту выхода электрона из дуанта 2 при помощи высокочастотного генератора изменяется направление электрического поля на обратное: дуант 1 приобретает отрицательный потенциал, а дуант 2 положительный. Поэтому ион вновь ускорится и внутри дуанта 1 опишет полуокружность уже большего радиуса (но время прохождения полуокружности останется неизменным!). Двигаясь в резонансе с высокочастотным полем, ионы будут по спирали приближаться к краю магнита, причем их энергия будет расти после каждого прохождения частицей ускоряющего промежутка между дуантами. Пучок ускоренных ионов выходит из циклотрона с помощью отклоняющего электрода, на который подается высокий отрицательный потенциал.
На рис. 5.17 показаны циклические ускорители заряженных частиц.
Рис. 5.17. Циклические ускорители элементарных частиц:
1 — первый советский циклотрон (1935);
2 — современный циклотрон для исследований в области управляемого термоядерного синтеза
Циклотрон используется в качестве ускорителя тяжелых элементарных заряженных частиц и многозарядных положительных ионов. Имеются причины принципиального характера, которые ограничивают возможности значительного увеличения энергии ионов в циклотроне. Период обращения в циклотроне пропорционален массе частицы
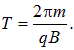
Однако в ускорителях, где частицы разгоняются до скоростей, близких к скорости света, приходится учитывать релятивистское выражение для импульса частицы. Тогда уравнение движения будет иметь вид
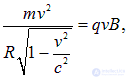
откуда для радиуса орбиты получаем
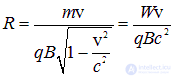
Здесь мы использовали выражение для релятивистской энергии W частицы
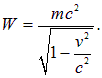
Находим тогда для периода обращения
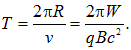
При малых кинетических энергиях
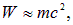
и мы возвращаемся к прежней формуле. Однако по мере ускорения частиц период обращения растет вместе с энергией, тогда как период высокочастотного поля в циклотроне не изменяется. В результате при каждом очередном попадании в ускоряющую щель частицы будут опаздывать, приобретая все меньшую энергию, пока не начнут попадать в тормозящее поле. Поэтому для достижения больших энергий частиц используется два приема:
Определение заряда и массы электрона
Уравнение движения (уравнение второго закона Ньютона) частицы массы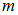 
с зарядом 
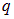, движущейся в электромагнитном поле, имеет вид
|
|
(5.16) |
Видно, что при любой конфигурации полей заряд и масса входят в виде отношения — удельного заряда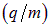 
. Поэтому, измеряя параметры траектории заряженной частицы в электромагнитном поле можно определить именно ее удельный заряд (рис. 5.18). Остается создать удобную для измерений конфигурацию электрического и магнитного полей.
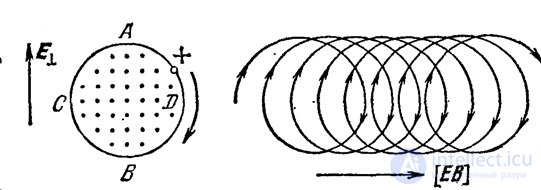
Рис. 5.18. Траектория движения заряженной частицы в скрещенных электрическом и магнитном поле
Рассмотрим заряженную частицу, движущуюся в пространстве со скоростью 
и попадающую в перпендикулярное к направлению ее движения однородное электрическое поле
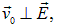
причем область поля имеет протяженность l1 (рис. 5.19).
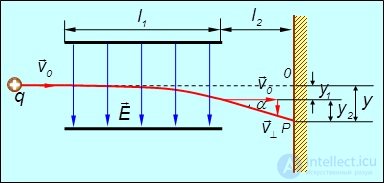
Рис. 5.19. Движение заряженной частицы в отклоняющем электрическом поле
В отсутствие поля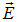 
частица попала бы в точку 0 на экране. На частицу же в поле действует сила F, направленная перпендикулярно скорости v0, из-за чего частица приобретает ускорение а = (q/m)E, где q/m — удельный заряд частицы. За время пролета области поля
частица сместится по вертикали на расстояние
|
|
(5.17) |
и приобретет составляющую скорости, перпендикулярную к направлению начальной скорости v0
Далее частица, вылетевшая из области действия поля, движется свободно, имея скорость
направленную под углом 
к первоначальной, причем
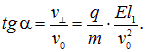
За время подлета к экрану частица успеет дополнительно сместиться на расстояние
|
|
(5.18) |
(см. рис. 5.19). В конечном итоге она попадает в точку P экрана, отстоящую от точки 0 на расстояние
|
|
(5.19) |
Полученные результаты позволяют сделать следующие выводы:
В 1897 г. Дж.Дж. Томсон впервые определил удельный заряд электрона е/m почти по такой схеме, использовав газоразрядную трубку (рис. 5.20). Электронный пучок проходил через отверстие в аноде и попадал в область однородного электрического поля конденсатора и перпендикулярного ему магнитного поля, создаваемого катушкой с током (на рис. 5.20 область магнитного поля показана пунктиром).
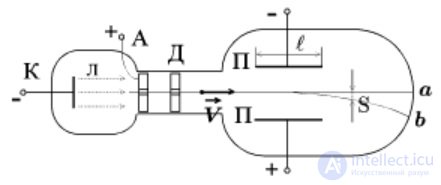
Рис. 5.20. Газоразрядная трубка, использовавшаяся для определения удельного заряда электрона
При выключении поля, пучок электронов, двигаясь в направлении начальной скорости v0, создавал светящееся пятно в точке 0 флуоресцирующего экрана. Включение магнитного поля вызывало смещение светящегося пятна на экране. Затем, подбирая величину напряженности Е электрического поля конденсаторов, можно было добиться, чтобы пучок электронов не смещался относительно точки 0. В этом случае действие на электроны электрического и магнитного полей взаимно компенсировалось, то есть выполнялось условие (в (5.20) учтено, что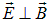 
)
|
|
(5.20) |
Зная напряженности полей, можно было определить скорость электронов v0 = E/B. Меняя поля и измеряя смещение светящегося пятна на экране, по скорости электронов и геометрическим размерам установки определяли удельный заряд электрона. Томсон получил
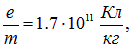
современное значение
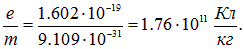
Масс-спектрометры
Для определения удельного заряда широко используются также приборы, называемые масс-спектрометрами или масс-спектрографами. Различие в названии приборов связано с различным способом регистрации ионов: при помощи электронных схем (масс-спектрометры) или при помощи фотографических пластинок (масс-спектрографы).
Различные типы этих приборов основаны на использовании фокусирующих свойств электрических и магнитных полей по отношению к заряженным частицам. Заряженные частицы (ионы или ядра) ускоряются электрическим полем (рис. 5.21).
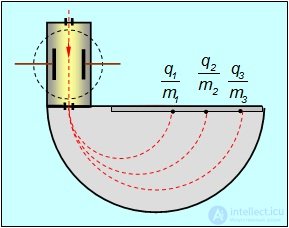
Рис. 5.21. Схема действия масс-спектрографа
После прохождения разности потенциалов U кинетическая энергия частиц равна
|
|
(5.21) |
где q = Ze — заряд иона (или ядра), m — масса иона, v — его скорость. Попадая в вакуумную камеру с однородным магнитным полем с магнитной индукцией В, перпендикулярной начальной скорости, частицы описывают полукруг (под влиянием силы Лоренца). Радиус окружности, по которой движется ион в магнитном поле, находится из условия
|
|
(5.22) |
Описав половину окружности, ионы попадают на фотопластинку на расстоянии 2R от щели. Решая совместно два уравнения — (5.21) и (5.22), получим
|
|
(5.23) |
Следовательно, ионы каждого сорта (определяемые значением q/m) в зависимости от величины отклоняющего магнитного и ускоряющего электрического полей попадают на фотопластинку в некоторое определенное место, характеризуемое величиной радиуса R. Зная параметры прибора, величины B и U, можно найти удельные заряды ионов.
В 1880 г. Э. Холл обнаружил, что в проводнике, помещенном в магнитное поле, возникает разность потенциалов в направлении, перпендикулярном вектору магнитной индукции B и току I. Объясняется это действием силы Лоренца на заряды, движущиеся в проводнике.
На рисунке 5.22 изображена пластина из проводника, которую пронизывает магнитное поле с индукцией B, направленное перпендикулярно чертежу от нас (обозначено крестиком).
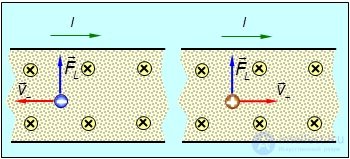
Рис. 5.22. При фиксированном направлении тока сила Лоренца,
действующая на носители зарядов в образце, помещенном в магнитное поле,
имеет одно и то же направление независимо от знака заряда носителя
У отрицательных зарядов вектор скорости v и ток I направлены в противоположные стороны, для положительных зарядов направления скорости и тока совпадают. Применяя правило винта, находим, что сила Лоренца в обоих случаях направлена к верхней грани пластины. Следовательно, носители зарядов, независимо от знака их заряда, накапливаются на верхней грани пластины.
Эффект Холла наблюдается у металлов и полупроводников. У металлов и полупроводников n-типа, где носителями зарядов являются электроны, на верхней грани пластины скапливаются избыточные отрицательные заряды, а нижняя грань заряжается положительно (рис. 5.23). У полупроводников p-типа, где носителями являются так называемые дырки, имеющие положительный заряд, верхняя грань заряжается положительно, а нижняя — отрицательно.
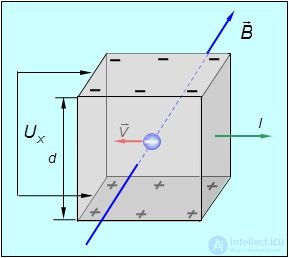
Рис. 5.23. Эффект Холла заключается в возникновении разности потенциалов UХ ,
между гранями проводящей пластины с током, помещенной в магнитное поле
(знаки зарядов показаны для металлической пластины)
Так как
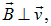
то сила Лоренца равна
|
|
(5.24) |
Заряды, скопившиеся на верхней и нижней границах пластины, создают электрическое поле напряженностью EX , которое в свою очередь воздействует на электрические заряды с силой
|
|
(5.25) |
Когда устанавливается стационарное распределение зарядов в поперечном сечении проводника, эти две силы уравновешивают друг друга
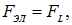
то есть
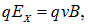
откуда
|
|
(5.26) |
Заметим, что здесь автоматически выполняется соотношение между скоростью зарядов и полями EX и B, с которым мы только что познакомились, обсуждая опыты Томсона по измерению удельного заряда электрона. При выполнении соотношения (5.26) заряд движется прямолинейно и равномерно в скрещенных электрическом и магнитном полях.
Из формулы для величины плотности тока j = qnv находим скорость упорядоченного движения зарядов
|
|
(5.27) |
Таким образом, для напряженности поперечного (холловского) электрического поля получаем
|
|
(5.28) |
Следовательно, при расстоянии между гранями пластины d разность потенциалов между ними равна
|
|
(5.29) |
где RX = 1/qn — коэффициент пропорциональности, называемый постоянной Холла. Плотность носителей зарядов (электронов) в металле n = 1028 м–3, откуда RX = 10–9 м3/Кл. Для наиболее распространенных полупроводников
RX = 0,1 м3/Кл.
Эффект Холла — один из эффективных методов изучения свойств носителей зарядов в металлах и полупроводниках. На рис. 5.24 представлен опыт, в котором демонстрируется возникновение поперечной ЭДС при внесении полупроводника с током в магнитное поле, перпендикулярное току. Плоский полупроводниковый образец, закрепленный на держателе, вносится в поле постоянного магнита, и вольтметр фиксирует наличие ЭДС Холла. При переворачивании образца относительно поля знак ЭДС меняется на противоположный.
Рис. 5.24. Эффект Холла в полупроводнике
Теперь мы готовы к обсуждению взаимодействия тока с магнитным полем.
Ампер установил наличие силового взаимодействия между двумя проводниками, по которым текут электрические токи. Пусть имеются два длинных параллельных проводника (рис. 5.25-1).
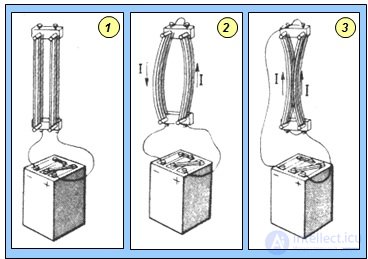
Рис. 5.25. Опыт Ампера по исследованию взаимодействия параллельных токов:
1 — схема установки; 2 — отталкивание антипараллельных токов; 3 — притяжение параллельных токов
Если по ним пропускать токи, текущие в противоположных направлениях, то проводники будут отталкиваться друг от друга (см. рис. 5.25-2). Если же токи будут течь в одном направлении, то они будут притягиваться (см. рис. 5.25-3).
Видео 5.4. Взаимодействие параллельных токов.
Эксперименты, проведенные Ампером, показали, что на проводник с током, помещенный в магнитное поле, действует сила. Откуда же она берется? Обсуждая эффект Холла, мы видели, что сила электрического поля EХ уравновешивает силу Лоренца, действующую на электроны. Но холловское поле EХ действует также и на кристаллическую ионную решетку вещества. На рис. 5.23 поле EХ направлено вверх, ортогонально току и магнитной индукции. Туда же будет направлена и сила, действующая на проводник. Найдем ее величину. Если поперечное сечение проводника равно S, а его длина (в направлении тока) — dl, то в данном объеме dV = dl · S сосредоточено dN = ndV = n · dl · S электронов проводимости. Их полный заряд равен dQ = edN = en · dl · S. В силу нейтральности проводника в целом таков же по абсолютной величине и полный заряд ионов кристаллической решетки. Используя формулу (5.28), находим суммарную силу, действующую на остов кристаллической решетки рассматриваемой части проводника
|
|
(5.30) |
где мы выразили плотность тока через его силу
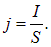
Обращаем внимание, что в эту формулу не вошли характеристики конкретных носителей заряда, но лишь полный ток через проводник.
У нас внешнее магнитное поле было ортогонально току. В общем случае направление тока будем характеризовать вектором dl, имеющем длину dl и направленным вдоль течения тока. В холловскую напряженность электрического поля дает вклад только компонента магнитного поля, ортогональная вектору dl. Эта компонента равна по величине
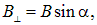
где есть угол между векторами B и dl. Тогда для величины силы имеем
|
|
(5.31) |
Учитывая направление этой силы (правило винта), можем записать ее в векторной форме
|
|
(5.32) |
Выражение (5.32) носит название закона Ампера, а сила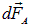 
называется силой Ампера (рис. 5.26).
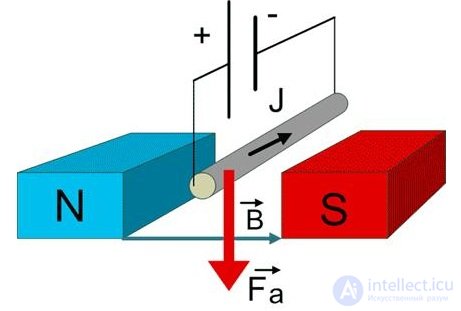
Рис. 5.26. Сила Ампера, действующая на провод с током в поле постоянного магнита
Видео 5.5. Сила Ампера: выпрыгивание провода из магнита.
Мы получили выражение для силы, действующей на элемент проводника dl. Для определения полной силы, действующей на проводник, надо проинтегрировать (5.32) вдоль его длины, учитывая зависимость магнитного поля от положения элемента. Такое интегрирование становится тривиальным для прямолинейного проводника в однородном магнитном поле
|
|
(5.33) |
Направление силы Ампера определяется по правилу левой руки (рис. 5.27):
|
Если левую руку расположить таким образом, чтобы линии магнитной индукции входили в ладонь, а вытянутые пальцы были направлены в направлении тока, то отогнутый большой палец покажет направление действия силы Ампера, действующей на проводник. |
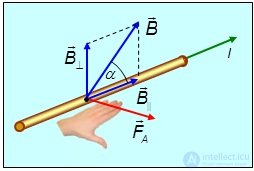
Рис. 5.27. Определение направления силы Ампера
Видео 5.6. Сила Ампера: тележка Эйхенвальда.
Действие силы Ампера на проводник с током демонстрируется в опыте, показанном на рис. 5.28. На торце вертикальной цилиндрической катушки положены горизонтальные проводящие рельсы, по которым может катиться алюминиевая трубка. После включения тока через катушку к рельсам прикладывается постоянное напряжение, и по трубке начинает течь ток. Под действием силы Ампера трубка катится по рельсам. При изменении направления тока в трубке она катится в противоположную сторону.
Рис. 5.28. Экспериментальное изучение силы Ампера
В общем случае произвольного проводника и магнитного поля силы, действующие на различные элементы проводника, различаются как величиной, так и направлением (рис. 5.29).
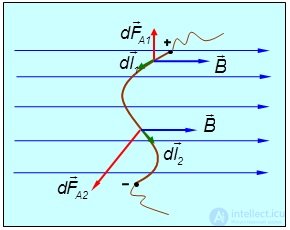
Рис. 5.29. В общем случае силы, действующие на различные элементы проводника,
различаются как величиной, так и направлением
С помощью формулы (5.31) можно определить величину магнитной индукции по максимальной силе Ампера dFA (в этом случае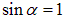 
), действующей на элемент dl проводника с током I
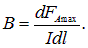
То есть величина магнитной индукции численно равна максимальной силе, действующей на единичный элемент тока.
Пусть контур с током помещен в магнитное поле, причем он может вращаться вокруг вертикальной оси OO' (рис. 5.30-1). Силы Ампера, действующие на стороны контура длиной l, перпендикулярны к ним и к магнитному полю и поэтому направлены вертикально: они лишь деформируют контур, стремясь растянуть его. Стороны, имеющие длину a, перпендикулярны B, так что на каждую из них действует сила F = BIa. Эти силы стремятся повернуть контур таким образом, чтобы его плоскость стала ортогональной B.
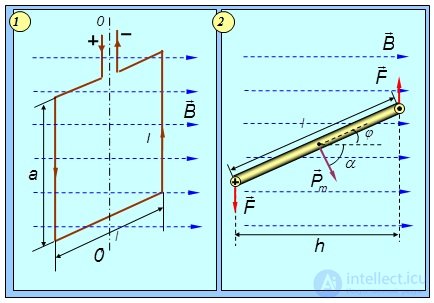
Рис. 5.30. Силы, действующие на контур с током в магнитном поле:
1 — вид сбоку; 2 — вид сверху (масштаб увеличен)
Видео 5.7. Контур с током в однородном магнитном поле.
Видео 5.8. Контур с током в неоднородном магнитном поле.
Момент пары сил (рис. 5.30-2) равен
|
|
(5.34) |
где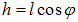 
— плечо пары сил, а 
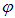— угол между вектором B и стороной l.
|
Величина, численно равная произведению силы тока I, протекающего в контуре, на площадь контура S = al называется магнитным моментом Pm плоского контура стоком
|
Таким образом, мы можем записать момент пары сил в виде
|
|
(5.36) |
Магнитный момент контура с током — векторная величина. Направление Рm совпадает с положительным направлением нормали к плоскости контура, которое определяется правилом винта: если рукоятка вращается по направлению тока в контуре, то поступательное движение винта показывает направление вектора Pm . Введем в формулу (15.36) угол a между векторами Pm и B. Справедливо соотношение
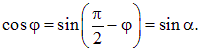
Следовательно,
|
|
(5.37) |
то есть момент сил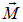 
, действующий на виток с током в однородном магнитном поле, равен векторному произведению магнитного момента 
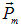витка на вектор индукции магнитного поля 
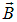(рис. 5.31). При 
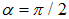величина момента сил максимальна
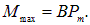
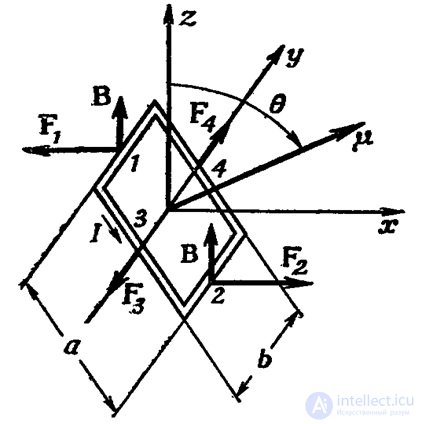
Рис. 5.31. Силы, действующие на прямоугольный контур с током в магнитном поле.
Магнитное поле вертикально, а магнитный момент перпендикулярен плоскости контура
Видео 5.9. Контур с током в магнитном поле: модель электродвигателя.
Опять-таки прозрачна аналогия с электростатикой: говоря об электрическом диполе, мы получили выражение для момента сил, действующих на него со стороны электрического поля в виде
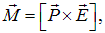
где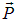 
— электрический дипольный момент.
|
В системе СИ единицей измерения магнитного момента контура является ампер на квадратный метр (А · м2)
|
Видео 5.10. «Сознательные катушки»: отталкивание и притяжение параллельных токов и поворот магнитного момента по магнитному полю.
Пример. По тонкому проводу в виде кольца радиусом 30 см течет ток 100 A. Перпендикулярно плоскости кольца возбуждено однородное магнитное поле с магнитной индукцией 20 мТл (рис. 5.32). Найти силу, растягивающую кольцо.
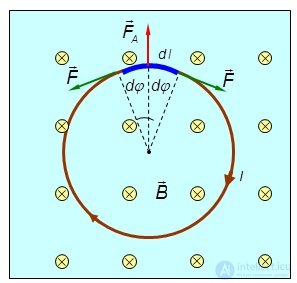
Рис. 5.32. Силы, растягивающие кольцо с током в магнитном поле
Решение. Пусть магнитное поле направлено от нас за плоскость рис. 5.32 (показано крестиками), а ток идет по часовой стрелке. Выделим элемент длины dl, видный из центра под углом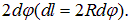 
На этот элемент действует сила Ампера 
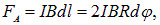направленная по радиусу кольца. Кроме того, из-за растяжения кольца на концы элемента действуют силы натяжения F, которые и требуется найти в задаче. Проекция этих сила на радиальное направление равна
Приравнивая эту проекцию силе Ампера, находим
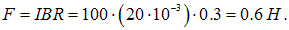
Исследование, описанное в статье про частицы в магнитном поле, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое частицы в магнитном поле и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Переменный электрический ток. Электромагнитное поле
Комментарии
Оставить комментарий
Базовая физика
Термины: Базовая физика