Лекция
Привет, Вы узнаете о том , что такое закон всемирного тяготения, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое закон всемирного тяготения, законы кеплера, гравитационные силы, принцип эквивалентности масс, потенциальная энергия гравитационного взаимодействия, космические скорости, определение масс небесных тел , настоятельно рекомендую прочитать все из категории Физические основы механики.
Согласно легенде, однажды в летний день 1665 г. И. Ньютон, созерцая окружающую природу, обратил внимание на падающее вниз яблоко. Если между Землей и яблоком существует притяжение, то такая же сила должна существовать и между любыми двумя телами с массами 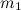 и
и 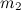 . Все тела в природе взаимно притягивают друг друга. Это взаимодействие называется гравитационным и является, как уже отмечалось в теме 3.3, одним из фундаментальных взаимодействий в природе.
. Все тела в природе взаимно притягивают друг друга. Это взаимодействие называется гравитационным и является, как уже отмечалось в теме 3.3, одним из фундаментальных взаимодействий в природе.
Мы знаем о нем очень мало, гораздо меньше, чем, например, об электромагнитном взаимодействии. Тем не менее, на уровне механики мы можем описать гравитацию, и это — очередное проявление разницы между вопросами «почему» и «как». О том же говорит старинный учебник физики, из которого взят эпиграф к настоящему курсу: «Не входя в исследование причин тяжести, приметим мы вообще только то, что ее называют обыкновенно притягательною силой Земли. Покуда самой вещи совершенно изъяснить не позволяется, то некоторым образом в сем положении оправдаться можно тем, что из различных наблюдений признали бытие такой притягательной в естестве силы».
Возможно, падающее яблоко и наводит на определенные мысли, но за 50 лет до Ньютона уже были известны количественные соотношения, которые прокладывали более прямой путь к установлению закона всемирного тяготения. Одним из величайших открытий в астрономии стали установленные И. Кеплером (1571–1630) законы движения планет:
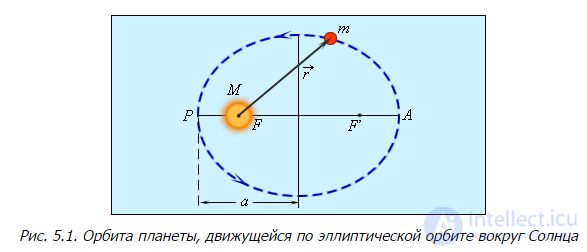
Рис. 5.1. Орбита планеты, движущейся по эллиптической орбите вокруг Солнца
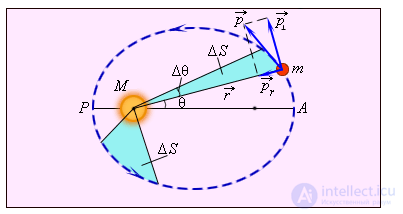
Коль скоро планеты обращаются вокруг Солнца благодаря силе, с которой светило действует на них, то законы Кеплера позволяют определить вид этой силы. Поместим начало координат в центр Солнца. Пусть  — радиус-вектор планеты, a
— радиус-вектор планеты, a 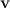 — ее скорость в данный момент времени. За время
— ее скорость в данный момент времени. За время 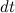 перемещение планеты равно
перемещение планеты равно 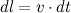 и направлено под углом а к радиус-вектору. Площадь
и направлено под углом а к радиус-вектору. Площадь 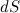 треугольника, образованного векторами
треугольника, образованного векторами  ,
, 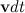 и
и  +
+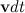 , равна
, равна  — (рис. 5.2).
— (рис. 5.2).

Рис. 5.2. Секториальная скорость
Согласно второму закону Кеплера, величина
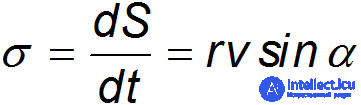
остается постоянной. Первый закон Кеплера утверждает, в частности, что орбита планеты лежит в одной плоскости. Это значит, что не зависит от времени вектор

величина которого равна 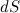 /
/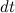 , а направление ортогонально плоскости орбиты. Этот вектор, называемый секториальной скоростью, пропорционален моменту импульса планеты
, а направление ортогонально плоскости орбиты. Этот вектор, называемый секториальной скоростью, пропорционален моменту импульса планеты
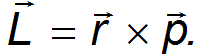
Отсюда следует, что силы, действующие на планету, — центральные: они направлены по линии, соединяющей Солнце с планетой, и зависят лишь от расстояния до Солнца.
Третий закон Кеплера позволяет установить зависимость сил от расстояния. Частный случай эллиптической орбиты - это круговая орбита, в центре которой находится Солнце. Тогда второй закон Кеплера сводится к утверждению о постоянстве угловой скорости  обращения планеты. Напомним, что угловая скорость обратно пропорциональна периоду обращения T:
обращения планеты. Напомним, что угловая скорость обратно пропорциональна периоду обращения T:
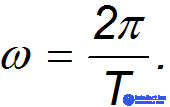
Для этого случая третий закон Кеплера утверждает, что отношение квадратов периодов обращения планет равен отношению кубов радиусов их орбит, то есть что квадраты периодов пропорциональны кубам радиусов орбит:
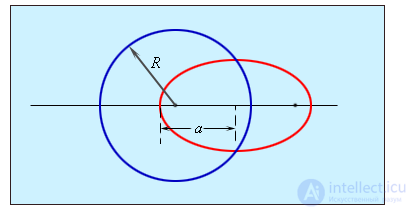
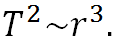
Отсюда следует, что квадраты угловых скоростей обратно пропорциональны кубам радиусов:

Комбинация  есть не что иное как нормальное ускорение, которое для равномерного вращения по окружности совпадает с полным ускорением
есть не что иное как нормальное ускорение, которое для равномерного вращения по окружности совпадает с полным ускорением  , где
, где  — масса планеты. Таким образом, получаем, что
— масса планеты. Таким образом, получаем, что
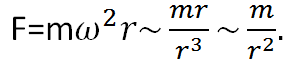
Таким образом, Солнце притягивает планету с силой, пропорциональной массе планеты и обратно пропорциональной квадрату расстояния до него:

Здесь 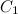 — коэффициент пропорциональности. Соответственно, планета притягивает Солнце с такой же силой, которая может быть выражена как
— коэффициент пропорциональности. Соответственно, планета притягивает Солнце с такой же силой, которая может быть выражена как

где 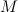 — масса Солнца, а
— масса Солнца, а 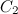 — какой-то другой коэффициент пропорциональности. Из равенства модулей (третий закон Ньютона) вытекает соотношение
— какой-то другой коэффициент пропорциональности. Из равенства модулей (третий закон Ньютона) вытекает соотношение

Обозначенное символом  отношение коэффициентов пропорциональности к массе называется гравитационной постоянной. Подставляя значения
отношение коэффициентов пропорциональности к массе называется гравитационной постоянной. Подставляя значения

в выражения для силы гравитации между Солнцем и планетой, находим
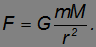

Рис. 5.3. Опыт Кавендиша по измерению силы гравитационного притяжения
Обобщая полученное соотношение, можно утверждать, что силы гравитации между любыми двумя телами определяются массами взаимодействующих тел и расстояниями между ними. Согласно установленному закону всемирного тяготения,
любые две материальные точки взаимодействуют с силой, пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними
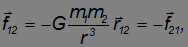
где гравитационная постоянная 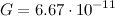 м3/(кг·с2), а
м3/(кг·с2), а 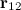 — радиус-вектор второго тела относительно первого (рис. 5.4). Знаки минус указывают на то, что силы
— радиус-вектор второго тела относительно первого (рис. 5.4). Знаки минус указывают на то, что силы 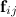 взаимодействия являются силами притяжения и противоположно направлены.
взаимодействия являются силами притяжения и противоположно направлены.
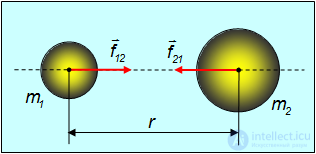
Рис. 5.4. Силы гравитации между двумя телами
Наиболее точно гравитационная постоянная определяется по изменению периода колебаний крутильных весов, вызванному приближением притягивающихся масс. Первые измерения относятся к концу XVIII столетия, из них классическим является опыт Г. Кавендиша (1798 г.).
Схема опыта Кавендиша заключается в использование крутильных весов (рис. 5.5).

Рис.5.5. Опыт Кавендиша: 1 — крутильные весы; 2 — вид сверху
На тонкой кварцевой нити подвешено коромысло с двумя небольшими свинцовыми шариками. При приближении к ним массивных свинцовых шаров нить закручивается. Измеряя угол поворота коромысла 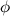 и зная модуль кручения нити, можно непосредственно измерить силу взаимодействия. Зная массы шаров и расстояние между ними, из закона всемирного тяготения можно определить гравитационную постоянную:
и зная модуль кручения нити, можно непосредственно измерить силу взаимодействия. Зная массы шаров и расстояние между ними, из закона всемирного тяготения можно определить гравитационную постоянную:
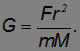
Функционирование установки, которую использовал Кавендиш, показано на рис. 5.3.
Если тела нельзя считать материальными точками, их представляют как совокупность материальных точек (частиц) и, геометрически суммируя силы взаимодействия отдельных частиц, находят результирующую силу тяготения между ними. Можно показать, что для тел идеально сферической формы закон гравитационного взаимодействия будет таким же, как и для материальных точек, если считать, что радиус-вектор 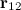 соединяет центры сфер (см. рис. 5.4).
соединяет центры сфер (см. рис. 5.4).
закон всемирного тяготения позволяет установить масштабы расстояний и масс в Солнечной системе.
Радиус Земли можно найти с помощью геометрических измерений на ее поверхности. Первым это сделал Эратосфен (276–194 г. до н.э.), нашедший для радиуса Земли величину R3 = 6 311 км. Эратосфен ошибся всего на 1 %: современное измерения для среднего радиуса Земли дают следующий результат: R3 = 6 371,03 км. В действительности Земля не является шаром, более точная модель «фигуры Земли» такая: сплюснутый эллипсоид вращения со средним экваториальным радиусом (большая полуось эллипсоида)  км и полярным радиусом (меньшая ось эллипсоида)
км и полярным радиусом (меньшая ось эллипсоида)  км. Эксцентриситет этого эллипсоида вращения весьма невелик
км. Эксцентриситет этого эллипсоида вращения весьма невелик 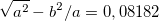 , поэтому в большинстве задач Землю, с вполне достаточной точностью, можно считать шаром.
, поэтому в большинстве задач Землю, с вполне достаточной точностью, можно считать шаром.
Схема опыта Эратосфена показана на рис. 5.6. В полдень в день летнего солнцестояния в городе Сиен (ныне Асуан) Солнце находилось в зените, и предметы не отбрасывали тени. В тот же день и в то же время в городе Александрия, находившемся в 5 000 стадиях от Сиена Солнце отклонялось от зенита примерно на 7°. Это составляет примерно 1/50 полного круга (360°), откуда получается, что окружность Земли равна 250 000 стадий.
Зная длину меридиана, можно узнать каким «стадием» пользовался Эратосфен, поскольку в древности в ходу были следующие стадии:
• вавилонский = 194 м
• греческий = 178 м
o аттический = 177,6 м
o олимпийский = 192,27 м
• египетский = 172,5 м
o стадий системы фараонов = 209,4 м
• птолемеевский и римский = 185 м
• стадий (гхальва) ассиро-халдейско-персидской системы = 230,4 м

Рис. 5.6. Опыт Эратосфена по определению радиуса Земли
Как найти массу Земли? Каждое тело массой  притягивается к ней с силой
притягивается к ней с силой

где  — масса Земли, а
— масса Земли, а  — расстояние от тела до центра Земли. Об этом говорит сайт https://intellect.icu . С другой стороны, отношение силы к массе — это ускорение свободного падения
— расстояние от тела до центра Земли. Об этом говорит сайт https://intellect.icu . С другой стороны, отношение силы к массе — это ускорение свободного падения  (вращением Земли пренебрегаем):
(вращением Земли пренебрегаем):
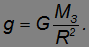
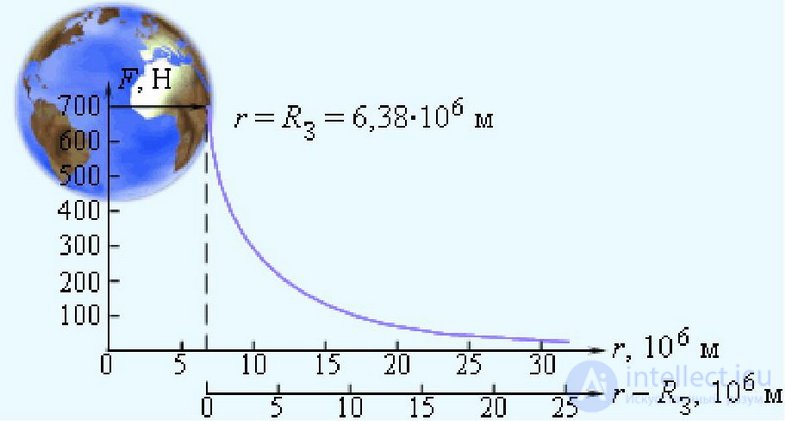
Отсюда следует, что  не зависит от массы и размеров тела и определяется исключительно параметрами Земли и расстоянием до нее. Вблизи поверхности Земли
не зависит от массы и размеров тела и определяется исключительно параметрами Земли и расстоянием до нее. Вблизи поверхности Земли

и  = 9,81 м/с2. Находим отсюда массу Земли:
= 9,81 м/с2. Находим отсюда массу Земли:

Ближайшим к Земле небесным телом является Луна. Определим расстояние 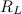 до Луны. Мы знаем, что период обращения Луны вокруг Земли равен
до Луны. Мы знаем, что период обращения Луны вокруг Земли равен 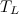 = 27,32 сут = 27,32·86 400 = 2,36·106 с. Центростремительное ускорение Луны
= 27,32 сут = 27,32·86 400 = 2,36·106 с. Центростремительное ускорение Луны
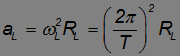
должно быть равно ускорению свободного падения на орбите Луны при  =
= 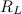 . Приравнивая
. Приравнивая  и
и 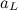 , находим:
, находим:
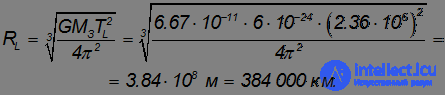
Скорость Луны на орбите равна

Легко определить угловой диаметр 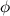 Луны: большой палец, толщина которого примерно равна 1 см, закрывает при вытянутой руке (то есть на расстоянии примерно 1 м) ее диск. Отсюда
Луны: большой палец, толщина которого примерно равна 1 см, закрывает при вытянутой руке (то есть на расстоянии примерно 1 м) ее диск. Отсюда
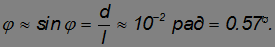
Более точные измерения дают для углового диаметра

Отсюда радиус Луны будет

Зная расстояние от Земли до Луны, с помощью геометрии можно определить расстояние от Земли до Солнца. Когда Луна находится в первой четверти, направления от нее в сторону Земли и в сторону Солнца составляют прямой угол (рис. 5.7).

Рис. 5.7. Геометрический метод определения расстояния от Земли до Солнца
Если в этот момент на Земле измерить угол 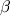 между направлениями на Луну и Солнце, то расстояние до Солнца определится как
между направлениями на Луну и Солнце, то расстояние до Солнца определится как

Угол 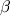 оказывается близким к прямому:
оказывается близким к прямому: 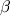 = 89°51'. Поэтому удобнее будет пользоваться дополнительным углом
= 89°51'. Поэтому удобнее будет пользоваться дополнительным углом 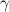 =
=  /2 – β = 9' = 0,15° = 0,0026 рад. Тогда расстояние до Солнца будет равно
/2 – β = 9' = 0,15° = 0,0026 рад. Тогда расстояние до Солнца будет равно
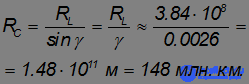
Это расстояние называется астрономической единицей (А или a.e., выше оно обозначено 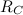 ). Более точно, A = 1,496·1011 м.
). Более точно, A = 1,496·1011 м.
Зная период обращения Земли вокруг Солнца  = 1 год = 365,25 сут = 3,156·107 с, находим скорость Земли на орбите:
= 1 год = 365,25 сут = 3,156·107 с, находим скорость Земли на орбите:
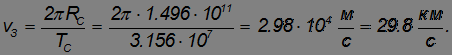
Наконец, мы определим параметры Солнца. Видимый с Земли угловой диаметр Солнца примерно таков же, как и у Луны: φ = 32' = 0,533° = 9,31·10–3 рад. Отсюда находим радиус Солнца:

Массу Солнца 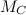 получаем из закона всемирного тяготения: центростремительное ускорение Земли на орбите
получаем из закона всемирного тяготения: центростремительное ускорение Земли на орбите

должно быть равно ускорению свободного падения Земли на Солнце

Приравнивая 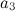 и
и 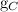 , получаем:
, получаем:
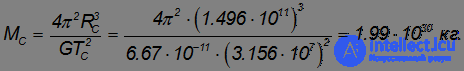
В этом выражении мы видим знакомую по третьему закону Кеплера комбинацию: отношение куба расстояния от планеты до Солнца к квадрату периода обращения. У всех планет это отношение одинаково, так как они вращаются вокруг одной и той же звезды.
Орбитальную скорость Земли можно также записать в виде
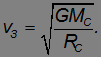
Это выражение справедливо для любой планеты при соответствующем изменении радиуса орбиты  .
.
Приведенные оценки показывают, как много можно узнать о мире, наблюдая его из удобного кресла и ... понимая законы природы.
В предыдущем разделе мы негласно предполагали, что инертная масса 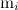 во втором законе Ньютона
во втором законе Ньютона
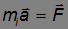
и гравитационная масса 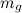 в законе всемирного тяготения
в законе всемирного тяготения

суть одно и то же. Строго говоря, к этому у нас пока не было оснований, кроме чисто филологического — в обоих законах использовано слово «масса». Но представим себе, что величину 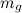 в законе всемирного тяготения мы называем не массой, а, скажем, гравитационным зарядом (по аналогии с зарядом электрическим). И сразу становится ясным, что вопрос о соотношении
в законе всемирного тяготения мы называем не массой, а, скажем, гравитационным зарядом (по аналогии с зарядом электрическим). И сразу становится ясным, что вопрос о соотношении 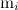 и
и 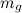 не решается столь просто. Ответ должен быть получен в экспериментах.
не решается столь просто. Ответ должен быть получен в экспериментах.
Инертная масса 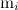 входит во второй закон Ньютона, и она характеризует инертные свойства тела. Гравитационная масса появилась в законе всемирного тяготения и отражает способность тел притягивать друг друга. Ускорение тела под действием сил гравитации у поверхности Земли может быть записано как
входит во второй закон Ньютона, и она характеризует инертные свойства тела. Гравитационная масса появилась в законе всемирного тяготения и отражает способность тел притягивать друг друга. Ускорение тела под действием сил гравитации у поверхности Земли может быть записано как
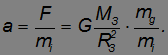
Совокупность опытных фактов указывает на то, что ускорение a одинаково для всех тел:

Значит, инертная масса и гравитационная масса всех тел строго пропорциональны друг другу, то есть их отношение 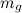 /
/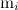 одно и то же для всех тел. Тогда единицу измерения гравитационной массы и гравитационную постоянную
одно и то же для всех тел. Тогда единицу измерения гравитационной массы и гравитационную постоянную 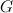 можно выбрать так, чтобы
можно выбрать так, чтобы 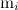 =
= 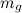 . Таким образом,
. Таким образом, 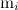 и
и 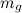 тождественны при надлежащем выборе единиц измерения.
тождественны при надлежащем выборе единиц измерения.
Постоянство отношения 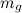 /
/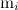 для всех тел является характерной особенностью гравитационного поля. Например, в электрическом поле мы не встречаемся ни с чем подобным: там отношение заряда тела к его массе
для всех тел является характерной особенностью гравитационного поля. Например, в электрическом поле мы не встречаемся ни с чем подобным: там отношение заряда тела к его массе  /
/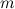 может принимать любые значения и меняется от тела к телу. Соответственно, не возникает вопрос об отождествлении электрического заряда и массы.
может принимать любые значения и меняется от тела к телу. Соответственно, не возникает вопрос об отождествлении электрического заряда и массы.
В пространстве, окружающем тела, что-то меняется: мы говорим, что они создают гравитационное поле. Энергетическая характеристика этого поля — потенциальная энергия взаимодействия двух гравитационных масс — определяется по общим правилам. Именно, градиент потенциальной энергии должен давать силу:

Для центральных сил

к которым относится и сила всемирного тяготения, это уравнение, как мы видели в предыдущем разделе, сводится к уравнению
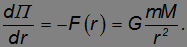
Отсюда
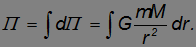
Интегрируя, получим
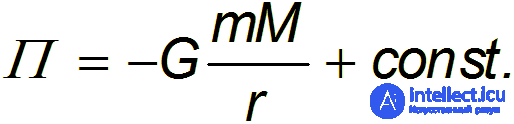
Постоянную интегрирования const принимают равной нулю, чтобы при  , стремящемся к бесконечности, потенциальная энергия гравитационного взаимодействия стремилась к нулю. Это не умаляет общности, так как физически наблюдаемой является разность потенциальных энергий, а не ее значение.
, стремящемся к бесконечности, потенциальная энергия гравитационного взаимодействия стремилась к нулю. Это не умаляет общности, так как физически наблюдаемой является разность потенциальных энергий, а не ее значение.
Рассмотрим изменение потенциальной энергии тела 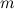 , перемещенного с поверхности Земли на высоту
, перемещенного с поверхности Земли на высоту  :
:
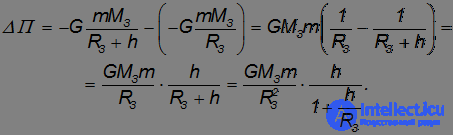
Учитывая, что

получаем
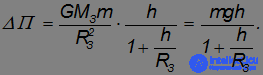
Если выбрать потенциальную энергию тела на поверхности Земли равной нулю, то 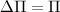 . При малых высотах
. При малых высотах 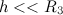 можно пренебречь отношением
можно пренебречь отношением  в знаменателе правой части полученной формулы для потенциальной энергии, что дает знакомое выражение
в знаменателе правой части полученной формулы для потенциальной энергии, что дает знакомое выражение

Космические скорости (первая v1, вторая v2, третья v3 и четвертая v4 ) — характерные критические скорости движения космических объектов в гравитационных полях небесных тел и их систем. Космические скорости используются для характеристики типа движения космического аппарата в сфере действия небесных тел: Солнца, Земли и Луны, других планет и их естественных спутников, а также астероидов и комет.
По определению, космическая скорость — это минимальная начальная скорость, которую необходимо придать объекту (например, космическому аппарату) на поверхности небесного тела в отсутствие атмосферы, чтобы:
Космические скорости могут быть рассчитаны для любого удаления от центра Земли. Однако в космонавтике часто используются величины, рассчитанные конкретно для поверхности шаровой однородной модели Земли радиусом 6371 км.

Применим закон всемирного тяготения для определения двух характерных «космических» скоростей, связанных с размерами и полем тяготения некоторой планеты. Планету будем считать одним шаром.

Рис. 5.8. Различные траектории движения спутников вокруг Земли
Пусть G является гравитационной постоянной , и пусть М быть масса земли (или другого тела гравитирующего) и т быть масса тела или отводящей снаряда. На расстоянии r от центра тяжести тело ощущает силу притяжения
Поэтому работа, необходимая для перемещения тела на небольшое расстояние dr против этой силы, определяется выражением
Тогда полная работа, необходимая для перемещения тела с поверхности r 0 гравитирующего тела на бесконечность, равна [15]
Чтобы выполнить эту работу, чтобы достичь бесконечности, минимальная кинетическая энергия тела при вылете должна соответствовать этой работе, поэтому скорость убегания v 0 удовлетворяет
что приводит к
Первой космической скоростью 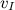 называют такую горизонтально направленную минимальную скорость, при которой тело могло бы двигаться вокруг Земли по круговой орбите, то есть превратиться в искусственный спутник Земли.
называют такую горизонтально направленную минимальную скорость, при которой тело могло бы двигаться вокруг Земли по круговой орбите, то есть превратиться в искусственный спутник Земли.
Это, конечно идеализация, во-первых планета не шар, во-вторых, если у планеты есть достаточно плотная атмосфера, то такой спутник — даже если его удастся запустить — очень быстро сгорит. Другое дело, что, скажем спутник Земли, летающий в ионосфере на средней высоте над поверхностью в 200 км имеет радиус орбиты отличающийся от среднего радиуса Земли всего, примерно, на 3 %.
На спутник, движущийся по круговой орбите радиусом  (рис. 5.9), действует сила притяжения Земли, сообщающая ему нормальное ускорение
(рис. 5.9), действует сила притяжения Земли, сообщающая ему нормальное ускорение

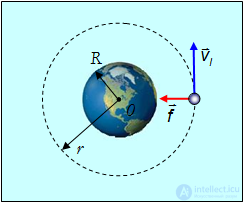
Рис. 5.9. Движение искусственного спутника Земли по круговой орбите
По второму закону Ньютона имеем
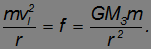
Если спутник движется недалеко от поверхности Земли, то

и
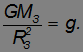
Поэтому для 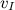 на Земле получаем
на Земле получаем
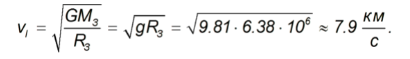
Видно ,что 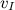 действительно определяется параметрами планеты:ее радиусом и массой.
действительно определяется параметрами планеты:ее радиусом и массой.
Период обращения спутника вокруг Земли равен
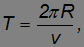
где  — радиус орбиты спутника, а
— радиус орбиты спутника, а  — его орбитальная скорость.
— его орбитальная скорость.
Минимальное значение периода обращения достигается при движении по орбите, радиус которой равен радиусу планеты:

так что первую космическую скорость можно определить и так: скорость спутника на круговой орбите с минимальным периодом обращения вокруг планеты.
Период обращения растет с увеличением радиуса орбиты.
Если период обращения спутника равен периоду обращения Земли вокруг своей оси и их направления вращения совпадают, а орбита расположена в экваториальной плоскости, то такой спутник называется геостационарным.
Геостационарный спутник постоянно висит над одной и той же точкой поверхности Земли (рис. 5.10).
Рис. 5.10. Движение геостационарного спутника
Для того чтобы тело могло выйти из сферы земного притяжения, то есть могло удалиться на такое расстояние, где притяжение к Земле перестает играть существенную роль, необходима вторая космическая скорость (рис. 5.11).
Второй космической скоростью 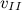 называют наименьшую скорость, которую необходимо сообщить телу, чтобы его орбита в поле тяготения Земли стала параболической, то есть чтобы тело могло превратиться в спутник Солнца.
называют наименьшую скорость, которую необходимо сообщить телу, чтобы его орбита в поле тяготения Земли стала параболической, то есть чтобы тело могло превратиться в спутник Солнца.
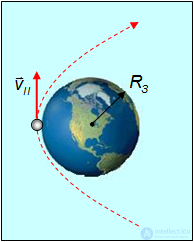
Рис. 5.11. Вторая космическая скорость
Для того чтобы тело (при отсутствии сопротивления среды) могло преодолеть земное притяжение и уйти в космическое пространство, необходимо, чтобы кинетическая энергия тела на поверхности планеты была равна (или превосходила) работу, совершаемую против сил земного притяжения. Напишем закон сохранения механической энергии Е такого тела. На поверхности планеты, конкретно — Земли

Скорость 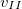 получится минимальной,если на бесконечном удалении от планеты тело будет покоиться
получится минимальной,если на бесконечном удалении от планеты тело будет покоиться
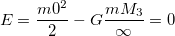
Приравнивая эти два выражения,получаем
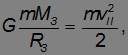
откуда для второй космической скорости имеем
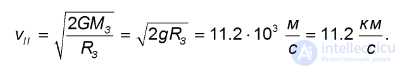
Для сообщения запускаемому объекту необходимой скорости (первой или второй космической) выгодно использовать линейную скорость вращения Земли, то есть запускать его как можно ближе к экватору, где эта скорость составляет, как мы видели, 463 м/с (точнее 465,10 м/с). При этом направление запуска должно совпадать с направлением вращения Земли — с запада на восток. Легко подсчитать, что таким способом можно выиграть несколько процентов в энергетических затратах.
В зависимости от начальной скорости  , сообщаемой телу в точке бросания А на поверхности Земли, возможны следующие виды движения (рис. 5.8 и 5.12):
, сообщаемой телу в точке бросания А на поверхности Земли, возможны следующие виды движения (рис. 5.8 и 5.12):
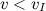 , то тело упадет на Землю.
, то тело упадет на Землю.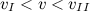 , то тело будет двигаться по эллиптической траектории.
, то тело будет двигаться по эллиптической траектории.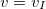 , то тело «уйдет на бесконечность» по парабалической траектории
, то тело «уйдет на бесконечность» по парабалической траектории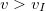 , то тело «уйдет на бесконечность» по гиперболической траектории.
, то тело «уйдет на бесконечность» по гиперболической траектории.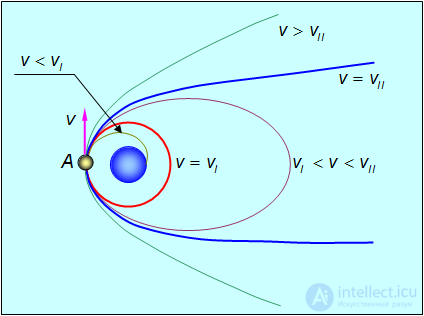
Рис. 5.12. Формы траектории частицы в зависимости от скорости бросания
Совершенно аналогично рассчитывается движение в гравитационном поле любого другого космического тела,например, Солнца. Чтобы преодолеть силу притяжения светила и покинуть Солнечную систему,объекту,покоящемусю относительно Солнца и находящемуся от него на расстоянии, равном радиусу земной орбиты 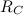 (см. выше), необходимо сообщить минимальную скорость
(см. выше), необходимо сообщить минимальную скорость  , определяемую из равенства
, определяемую из равенства
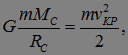
где 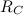 , напомним, это радиус земной орбиты, а
, напомним, это радиус земной орбиты, а 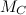 — масса Солнца.
— масса Солнца.
Отсюда следует формула, аналогичная выражению для второй космической скорости, где надо заменить массу Земли на массу Солнца и радиус Земли на радиус земной орбиты:

Подчеркнем, что  — это минимальная скорость, которую надо придать неподвижному телу, находящемуся на земной орбите, чтобы оно преодолело притяжение Солнца.
— это минимальная скорость, которую надо придать неподвижному телу, находящемуся на земной орбите, чтобы оно преодолело притяжение Солнца.
Отметим также связь
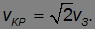
с орбитальной скоростью Земли  . Эта связь, как и должно быть — Земля спутник Солнца, такая же, как и между первой и второй космическими скоростями
. Эта связь, как и должно быть — Земля спутник Солнца, такая же, как и между первой и второй космическими скоростями 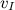 и
и 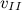 .
.
На практике мы запускаем ракету с Земли, так что она заведомо участвует в орбитальном движении вокруг Солнца. Как было показано выше, Земля движется вокруг Солнца с линейной скоростью

Ракету целесообразно запускать в направлении движения Земли вокруг Солнца.
Скорость, которую необходимо сообщить телу на Земле, чтобы оно навсегда покинуло пределы Солнечной системы, называется третьей космической скоростью 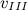 .
.
Скорость 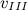 зависит от того, в каком направлении космический корабль выходит из зоны действия земного притяжения. При оптимальном запуске эта скорость составляет приблизительно
зависит от того, в каком направлении космический корабль выходит из зоны действия земного притяжения. При оптимальном запуске эта скорость составляет приблизительно 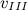 = 6,6 км/с.
= 6,6 км/с.
Понять происхождение этого числа можно также из энергетических соображений. Казалось бы, достаточно ракете сообщить относительно Земли скорость

в направлении движения Земли вокруг Солнца, и она покинет пределы Солнечной системы. Но это было бы правильно, если бы Земля не имела собственного поля тяготения. Такую скорость тело должно иметь, уже удалившись из сферы земного притяжения. Поэтому подсчет третьей космической скорости очень похож на вычисление второй космической скорости, но с дополнительным условием — тело на большом расстоянии от Земли должно все еще иметь скорость  :
:
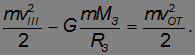
В этом уравнении мы можем выразить потенциальную энергию тела на поверхности Земли (второе слагаемое в левой части уравнения) через вторую космическую скорость 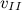 в соответствии с полученной ранее формулой для второй космической скорости
в соответствии с полученной ранее формулой для второй космической скорости
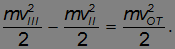
Отсюда находим
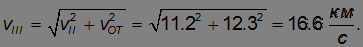
Ньютон доказал, что более точная формула третьего закона Кеплера такова:

где M1 и М2 - массы каких-либо небесных тел, a m1 и m2 - соответственно массы их спутников. Так, планеты считаются спутниками Солнца. Мы видим, что уточненная формула этого закона отличается от приближенной наличием множителя, содержащего массы. Если под M1=M2=M понимать массу Солнца, а под m1 и m2 - массы двух разных планет, то отношение
понимать массу Солнца, а под m1 и m2 - массы двух разных планет, то отношение  будет мало отличаться от единицы, так как m1 и m2 очень малы по сравнению с массой Солнца. При этом точная формула не будет заметно отличаться от приближенной.
будет мало отличаться от единицы, так как m1 и m2 очень малы по сравнению с массой Солнца. При этом точная формула не будет заметно отличаться от приближенной.
Уточненный третий закон Кеплера позволяет определить массы планет, имеющих спутников, и массу Солнца. Чтобы определить массу Солнца, будем сравнивать движение Луны вокруг Земли с движением Земли вокруг Солнца:

где Т и а
и а - период обращения Земли (год) и большая полуось ее орбиты, T
- период обращения Земли (год) и большая полуось ее орбиты, T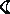 и а
и а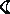 - период обращения Луны вокруг Земли и большая полуось ее орбиты, М
- период обращения Луны вокруг Земли и большая полуось ее орбиты, М - масса Солнца, М
- масса Солнца, М - масса Земли, m
- масса Земли, m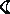 -масса Луны. Масса Земли ничтожна по сравнению с массой Солнца, а масса Луны мала (1:81) по сравнению с массой Земли. Поэтому вторые слагаемые в суммах можно отбросить, не делая большой ошибки. Решив уравнение относительно
-масса Луны. Масса Земли ничтожна по сравнению с массой Солнца, а масса Луны мала (1:81) по сравнению с массой Земли. Поэтому вторые слагаемые в суммах можно отбросить, не делая большой ошибки. Решив уравнение относительно  имеем:
имеем:

Эта формула позволяет определить массу Солнца, выраженную в массах Земли. Она составляет около 333 000 масс Земли.
Для сравнения масс Земли и другой планеты, например Юпитера, надо в исходной формуле индекс 1 отнести к движению Луны вокруг Земли массой M1, a 2 - к движению любого спутника вокруг Юпитера массой М2.
Массы планет, не имеющих спутников, определяют по тем возмущениям, которые они своим притяжением производят в движении соседних с ними планет, а также в движении комет, астероидов или космических аппаратов.
1. Определите массу Юпитера сравнением системы Юпитера со спутником с системой Земля - Луна, если первый спутник Юпитера отстоит от него на 422 000 км и имеет период обращения 1,77 сут. Данные для Луны должны быть вам известны.
2. Вычислите, на каком расстоянии от Земли на линии Земля - Луна находятся те точки, в которых притяжения Землей и Луной одинаковы, зная, что расстояние между Луной и Землей равно 60 радиусам Земли, а масса Земли в 81 раз больше массы Луны.
Исследование, описанное в статье про закон всемирного тяготения, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое закон всемирного тяготения, законы кеплера, гравитационные силы, принцип эквивалентности масс, потенциальная энергия гравитационного взаимодействия, космические скорости, определение масс небесных тел и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Физические основы механики
Комментарии
Оставить комментарий
Физические основы механики
Термины: Физические основы механики