Лекция
Сразу хочу сказать, что здесь никакой воды про закон сохранения, и только нужная информация. Для того чтобы лучше понимать что такое закон сохранения, превращения энергии, теорема кёнига , настоятельно рекомендую прочитать все из категории Физические основы механики.
Зако́н сохране́ния эне́ргии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда закономерность, его можно именовать не законом, а принципом сохранения энергии.
С фундаментальной точки зрения, согласно теореме Нетер, закон сохранения энергии является следствием однородности времени, то есть независимости законов физики от момента времени, в который рассматривается система. В этом смысле закон сохранения энергии является универсальным, то есть присущим системам самой разной физической природы. При этом выполнение этого закона сохранения в каждой конкретно взятой системе обосновывается подчинением этой системы своим специфическим законам динамики, вообще говоря, различающимся для разных систем.
В различных разделах физики по историческим причинам закон сохранения энергии формулировался независимо, в связи с чем были введены различные виды энергии. Возможен переход энергии из одного вида в другой, но полная энергия системы, равная сумме отдельных видов энергий, сохраняется. Однако, из-за условности деления энергии на различные виды, такое деление не всегда может быть произведено однозначно.
Для каждого вида энергии закон сохранения может иметь свою, отличающуюся от универсальной, формулировку. Например, в классической механике был сформулирован закон сохранения механической энергии, в термодинамике — первое начало термодинамики, а в электродинамике — теорема Пойнтинга.
С математической точки зрения, закон сохранения энергии эквивалентен утверждению, что система дифференциальных уравнений, описывающая динамику данной физической системы, обладает первым интегралом движения, связанным с симметричностью уравнений относительно сдвига во времени.
Рассмотрим процесс изменения состояния тела, поднятого на высоту h. При этом его потенциальная энергия
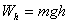
Тело начало свободно падать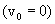 
. Из кинематики известно, что момент достижения поверхности земли оно будет иметь скорость 
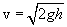икинетическую энергию:
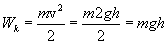
Кинетическая энергия тела, упавшего с высоты h, оказалась равной его потенциальной энергии, которую оно имело до начала падения. Следовательно:
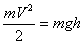
На поверхности Земли h=0 и потенциальная энергия 
, а 
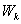-максимальна. В начале падения 
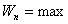, а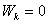
т.е. потенциальная энергия переходит (превращается) в кинетическую. Таким образом, при падении тела в системе тело-Земля кинетическая энергия возрастает и, следовательно, ее изменение 
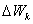равное работе 
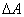, имеет положительный знак, т.е.
 |
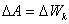(4.12) |
Потенциальная энергия - уменьшается, и, следовательно, ее изменение имеет знак минус. Поэтому можем записать:
 |
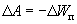(4.13) |
Сложив (4.12) и (4.13), получим
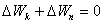
или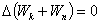 
Сумма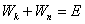 
представляет собой полную энергию, и, следовательно,
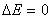, а
 |
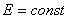(4.14) |
Таким образом, энергия замкнутой консервативной системы остается постоянной при всех, происходящих в ней процессах и превращениях. Энергия может переходить из одних видов в другие (механические, тепловые, и т.д.), но общее ее количество остается постоянным. Данное положение называют законом сохранения и превращения энергии .
Теоре́ма Кенига позволяет выразить полную кинетическую энергию механической системы через энергию движения центра масс и энергию движения относительно центра масс. Сформулирована и доказана И. С. Кенигом в 1751 г.
Кинетическая энергия механической системы есть энергия движения центра масс плюс энергия движения относительно центра масс:
где 
— полная кинетическая энергия системы, 
— кинетическая энергия движения центра масс, 
— относительная кинетическая энергия системы .
Иными словами, полная кинетическая энергия тела или системы тел в сложном движении равна сумме энергии системы в поступательном движении и энергии системы в ее движении относительно центра масс.
Более точная формулировка :
Кинетическая энергия системы материальных точек равна сумме кинетической энергии всей массы системы, мысленно сосредоточенной в ее центре масс и движущейся вместе с ним, и кинетической энергии той же системы в ее относительном движении по отношению к поступательно движущейся системе координат с началом в центре масс.
Приведем доказательство теоремы Кенига для случая, когда массы тел, образующих механическую систему 
, распределены непрерывно .
Найдем относительную кинетическую энергию системы , трактуя ее как кинетическую энергию, вычисленную относительно подвижной системы координат. Пусть 
— радиус-вектор рассматриваемой точки системы в подвижной системе координат. Тогда :
где точкой обозначено скалярное произведение, а интегрирование ведется по области пространства, занимаемой системой в текущий момент времени.
Если 
— радиус-вектор начала координат подвижной системы, а 
— радиус-вектор рассматриваемой точки системы в исходной системе координат, то верно соотношение:
Вычислим полную кинетическую энергию системы в случае, когда начало координат подвижной системы помещено в ее центр масс. С учетом предыдущего соотношения имеем:
Учитывая, что радиус-вектор одинаков для всех 
, можно, раскрыв скобки, вынести 
за знак интеграла:
Первое слагаемое в правой части этой формулы (совпадающее с кинетической энергией материальной точки, которая помещена в начало координат подвижной системы и имеет массу, равную массе механической системы) может интерпретироваться как кинетическая энергия движения центра масс.
Второе слагаемое равно нулю, поскольку второй сомножитель в нем получается дифференцированием по времени произведения радиус-вектора центра масс на массу системы , но упомянутый радиус-вектор (а с ним и все произведение) равен нулю:
так как начало координат подвижной системы находится (по сделанному предположению) в центре масс.
Третье же слагаемое, как было уже показано, равно , т. е. относительной кинетической энергии системы .
| Симметрия в физике | ||
|---|---|---|
| Преобразование | Соответствующая инвариантность |
Соответствующий закон сохранения |
| ⭥Трансляции времени | Однородность времени |
…энергии |
| ⊠ C, P, CP и T-симметрии | Изотропность времени |
…четности |
| ⭤ Трансляции пространства | Однородность пространства |
…импульса |
| ↺ Вращения пространства | Изотропность пространства |
…момента импульса |
| ⇆ Группа Лоренца (бусты) | Относительность Лоренц-ковариантность |
…движения центра масс |
| ~ Калибровочное преобразование | Калибровочная инвариантность | …заряда |
Фундаментальный смысл закона сохранения энергии раскрывается теоремой Нетер. Согласно этой теореме, каждый закон сохранения однозначно соответствует той или иной симметрии уравнений, описывающих физическую систему. В частности, закон сохранения энергии эквивалентен однородности времени, то есть независимости всех законов, описывающих систему, от момента времени, в который система рассматривается.
Вывод этого утверждения может быть произведен, например, на основе лагранжева формализма . Если время однородно, то функция Лагранжа, описывающая систему, не зависит явно от времени, поэтому полная ее производная по времени имеет вид:
Здесь 
— функция Лагранжа, 
— обобщенные координаты и их первые и вторые производные по времени соответственно. Воспользовавшись уравнениями Лагранжа, заменим производные 
на выражение 
:
Перепишем последнее выражение в виде
Сумма, стоящая в скобках, по определению называется энергией системы и в силу равенства нулю полной производной от нее по времени она является интегралом движения (то есть сохраняется).
В ньютоновской механике формулируется частный случай закона сохранения энергии — Закон сохранения механической энергии, звучащий следующим образом :
Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остается постоянной.
Проще говоря, при отсутствии диссипативных сил (например, сил трения) механическая энергия не возникает из ничего и не может исчезнуть в никуда.
Классическим примером справедливости этого утверждения являются пружинный или математический маятники с пренебрежимо малым затуханием. В случае пружинного маятника в процессе колебаний потенциальная энергия деформированной пружины (имеющая максимум в крайних положениях груза) переходит в кинетическую энергию груза (достигающую максимума в момент прохождения грузом положения равновесия) и обратно . В случае математического маятника аналогично ведет себя потенциальная энергия груза в поле силы тяжести.
Закон сохранения механической энергии может быть выведен из второго закона Ньютона , если учесть, что в консервативной системе все силы, действующие на тело, потенциальны и, следовательно, могут быть представлены в виде
где 
— потенциальная энергия материальной точки ( — радиус-вектор точки пространства). Об этом говорит сайт https://intellect.icu . В этом случае второй закон Ньютона для одной частицы имеет вид
где 
— масса частицы, 
— вектор ее скорости. Скалярно домножив обе части данного уравнения на скорость частицы и приняв во внимание, что 
, можно получить
Путем элементарных операций это выражение может быть приведено к следующему виду
Отсюда непосредственно следует, что выражение, стоящее под знаком дифференцирования по времени, сохраняется. Это выражение и называется механической энергией материальной точки. Первый член в сумме отвечает кинетической энергии, второй — потенциальной.
Этот вывод может быть легко обобщен на систему материальных точек .
Уравнения Лагранжа голономной механической системы с не зависящей от времени функцией Лагранжа и потенциальными силами
имеют обобщенный интеграл энергии :
В термодинамике исторически закон сохранения формулируется в виде первого принципа термодинамики:
Изменение внутренней энергии термодинамической системы при переходе ее из одного состояния в другое равно сумме работы внешних сил над системой и количества теплоты, переданного системе, и не зависит от способа, которым осуществляется этот переход
или альтернативно :
Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы против внешних сил
В математической формулировке это может быть выражено следующим образом:
где введены обозначения 
— количество теплоты, полученное системой, 
— изменение внутренней энергии системы, 
— работа, совершенная системой.
Закон сохранения энергии, в частности, утверждает, что не существует вечных двигателей первого рода, то есть невозможны такие процессы, единственным результатом которых было бы производство работы без каких-либо изменений в других телах .
В гидродинамике идеальной жидкости закон сохранения энергии традиционно формулируется в виде уравнения Бернулли: вдоль линий тока остается постоянной сумма
Здесь введены следующие обозначения: 
— скорость потока жидкости, 
— тепловая функция жидкости, 
— ускорение свободного падения, 
— координата точки в направлении силы тяжести. Если внутренняя энергия жидкости не меняется (жидкость не нагревается и не охлаждается), то уравнение Бернулли может быть переписано в виде[10]
где 
— давление жидкости, 
— плотность жидкости. Для несжимаемой жидкости плотность является постоянной величиной, поэтому в последнем уравнении может быть выполнено интегрирование[10]:
В электродинамике закон сохранения энергии исторически формулируется в виде теоремы Пойнтинга[11][12](иногда также называемой теоремой Умова—Пойнтинга[13]), связывающей плотность потока электромагнитной энергии с плотностью электромагнитной энергии и плотностью джоулевых потерь. В словесной форме теорема может быть сформулирована следующим образом:
Изменение электромагнитной энергии, заключенной в неком объеме, за некий интервал времени равно потоку электромагнитной энергии через поверхность, ограничивающую данный объем, и количеству тепловой энергии, выделившейся в данном объеме, взятой с обратным знаком.
Математически это выражается в виде (здесь и ниже в разделе использована гауссова система единиц)
где 
— некий объем, 
— поверхность, ограничивающая этот объем,
— плотность электромагнитной энергии,
— вектор Пойнтинга,
— плотность тока, 
— напряженность электрического поля, 
— индукция электрического поля, 
— напряженность магнитного поля, 
— индукция магнитного поля.
Этот же закон математически может быть записан в дифференциальной форме:
В нелинейной оптике рассматривается распространение оптического (и вообще электромагнитного) излучения в среде с учетом многоквантового взаимодействия этого излучения с веществом среды. В частности, широкий круг исследований посвящен задачам так называемых трех- и четырехволнового взаимодействий, в которых происходит взаимодействие, соответственно, трех или четырех квантов излучения. Поскольку каждый отдельный акт такого взаимодействия подчиняется законам сохранения энергии и импульса, существует возможность сформулировать достаточно общие соотношения между макроскопическими параметрами взаимодействующих волн. Эти соотношения носят название соотношений Мэнли — Роу.
В качестве примера рассмотрим явление сложения частот света: генерацию в нелинейной среде излучения с частотой 
, равной сумме частот двух других волн 
и 
. Этот процесс является частным случаем трехволновых процессов: при взаимодействии двух квантов исходных волн с веществом они поглощаются с испусканием третьего кванта. Согласно закону сохранения энергии, сумма энергий двух исходных квантов должна быть равна энергии нового кванта:
Из этого равенства непосредственно следует одно из соотношений Мэнли — Роу:
которое, собственно, и выражает тот факт, что частота генерируемого излучения равна сумме частот двух исходных волн.
В релятивистской механике вводится понятие 4-вектора энергии-импульса (или просто четырехимпульса)[14]. Его введение позволяет записать законы сохранения канонического импульса и энергии в единой форме, которая к тому же является лоренц-ковариантной, то есть не меняется при переходе из одной инерциальной системы отсчета в другую. Например, при движении заряженной материальной точки в электромагнитном поле ковариантная форма закона сохранения имеет вид
где 
— канонический четырехимпульс частицы, 
— четырехимпульс частицы, 
— энергия частицы, 
— четырехвектор потенциала электромагнитного поля 
, — электрический заряд и масса частицы, 
— собственное время частицы.
Также важным является тот факт, что даже при невыполнении закона сохранения энергии-импульса (например, в открытой системе) сохраняется модуль этого 4-вектора, с точностью до размерного множителя имеющий смысл энергии покоя частицы[14]:
В квантовой механике также возможно формулирование закона сохранения энергии для изолированной системы. Так, в шредингеровском представлении при отсутствии внешних переменных полей гамильтониан системы не зависит от времени и можно показать[15], что волновая функция, отвечающая решению уравнения Шредингера, может быть представлена в виде:
Здесь 
— волновая функция системы, 
— совокупность переменных, от которых зависит состояние системы в данном представлении, 
— собственные функции и собственные значения оператора Гамильтона, 
— постоянная Планка, 
— некоторые постоянные комплексные коэффициенты, характеризующие состояние системы. По определению, средней энергией квантовой системы, описываемой волновой функцией, называется интеграл
где 
— гамильтониан системы. Несложно видеть, что этот интеграл не зависит от времени:
где также использовано свойство ортонормированности собственных функций гамильтониана[16]. Таким образом, энергия замкнутой системы сохраняется.
Следует, однако, отметить, что по сравнению с классической механикой у квантового закона сохранения энергии имеется одно существенное отличие. Дело в том, что для экспериментальной проверки выполнения закона необходимо провести измерение, представляющее собой взаимодействие исследуемой системы с неким прибором. В процессе измерения система, вообще говоря, более не является изолированной и ее энергия может не сохраняться (происходит обмен энергией с прибором). В рамках классической физики, однако, это влияние прибора всегда может быть сделано сколь угодно малым, в то время как в квантовой механике имеются фундаментальные ограничения на то, насколько малым может быть возмущение системы в процессе измерения. Это приводит к так называемому принципу неопределенности Гейзенберга, который в математической формулировке может быть выражен в следующем виде:
где 
имеет смысл среднеквадратичного отклонения измеренного значения энергии от среднего значения при проведении серии измерений, 
— продолжительность взаимодействия системы с прибором в каждом из измерений.
В связи с наличием этого фундаментального ограничения на точность измерений в квантовой механике часто говорят о законе сохранения средней энергии (в смысле среднего значения энергии, полученного в результате серии измерений).
Являясь обобщением специальной теории относительности, общая теория относительности пользуется обобщением понятия четырехимпульса — тензором энергии-импульса. Закон сохранения формулируется для тензора энергии-импульса системы и в математической форме имеет вид[17]
где точка с запятой выражает ковариантную производную.
В общей теории относительности закон сохранения энергии, строго говоря, выполняется только локально. Связано это с тем фактом, что этот закон является следствием однородности времени, в то время как в общей теории относительности время неоднородно и испытывает изменения в зависимости от наличия тел и полей в пространстве-времени. Следует отметить, что при должным образом определенном псевдотензоре энергии-импульса гравитационного поля можно добиться сохранения полной энергии гравитационно взаимодействующих тел и полей, включая гравитационное[18]. Однако на данный момент не существует общепризнанного способа введения энергии гравитационного поля, поскольку все предложенные варианты обладают теми или иными недостатками. Например, энергия гравитационного поля принципиально не может быть определена как тензор относительно общих преобразований координат[19].
Философские предпосылки к открытию закона были заложены еще античными философами. Ясную, хотя еще не количественную, формулировку дал в «Началах философии» (1644) Рене Декарт[20]:
Когда одно тело сталкивается с другим, оно может сообщить ему лишь столько движения, сколько само одновременно потеряет, и отнять у него лишь столько, насколько оно увеличит свое собственное движение.
Но Декарт под количеством движения понимал произведение массы на абсолютную величину скорости, то есть модуль импульса.
Лейбниц в своих трактатах «Доказательство памятной ошибки Декарта» (1686) и «Очерк динамики» (1695) ввел понятие «живой силы» (Vis viva), которую он определил как произведение массы объекта и квадрата его скорости (в современной терминологии — кинетическая энергия, только удвоенная). Кроме того, Лейбниц верил в сохранение общей «живой силы». Для объяснения замедления из-за трения он предположил, что утраченная часть «живой силы» переходит к атомам:
«То, что поглощается мельчайшими атомами, не теряется, безусловно, для вселенной, хотя и теряется для общей силы сталкивающихся тел»[21]
Но никаких экспериментальных доказательств своей догадке Лейбниц не привел. О том, что тепло и есть та самая энергия, забираемая атомами, Лейбниц еще не думал.
Точку зрения, аналогичную декартовской, выразил в XVIII веке М. В. Ломоносов[22]. В письме к Эйлеру (5 июля 1748 года) он сформулировал «всеобщий естественный закон», повторяя его в диссертации «Рассуждение о твердости и жидкости тел» (1760)[23][24]:
Все перемены, в натуре случающиеся, такого суть состояния, что сколько чего у одного тела отнимется, столько присовокупится к другому, так ежели где убудет несколько материи, то умножится в другом месте… Сей всеобщий естественный закон простирается и в самые правила движения, ибо тело, движущее своею силою другое, столько же оные у себя теряет, сколько сообщает другому, которое от него движение получает[25].
Одним из первых экспериментов, подтверждавших закон сохранения энергии, был эксперимент Жозефа Луи Гей-Люссака, проведенный в 1807 году. Пытаясь доказать, что теплоемкость газа зависит от объема, он изучал расширение газа в пустоту и обнаружил, что при этом его температура не изменяется. Однако, объяснить этот факт ему не удалось[22].
В начале XIX века рядом экспериментов было показано, что электрический ток может оказывать химическое, тепловое, магнитное и электродинамическое действия. Такое многообразие подвигло М. Фарадея выразить мнение, заключающееся в том, что различные формы, в которых проявляются силы материи, имеют общее происхождение, то есть могут превращаться друг в друга[26]. Эта точка зрения, по своей сути, предвосхищает закон сохранения энергии.
Первые работы по установлению количественной связи между совершенной работой и выделившейся теплотой были проведены Сади Карно[26]. В 1824 году им была опубликована небольшая брошюра «Размышления о движущей силе огня и о машинах, способных развивать эту силу» (фр. Réflexions sur la puissance motrice du feu et sur les machines propres а développer cette puissance[27]), которая вначале не получила большой известности, и была случайно обнаружена Клапейроном через 10 лет после издания. Клапейрон придал изложению Карно современную аналитическую и графическую форму и переопубликовал работу под тем же названием в журнале «Journal de l'École polytechnique» (фр.)русск.. Позднее была также перепечатана в «Анналах Поггендорфа». После ранней смерти Карно от холеры остались дневники, которые были опубликованы его братом. В них, в частности, Карно пишет[28]:
Тепло не что иное, как движущая сила, или, вернее, движение, изменившее свой вид. Это движение частиц тела. Повсюду, где происходит уничтожение движущей силы, возникает одновременно теплота в количестве, точно пропорциональном количеству исчезнувшей движущей силы. Обратно: при исчезновении теплоты всегда возникает движущая сила
Доподлинно неизвестно, какие именно размышления привели Карно к этому выводу, но по своей сути они являются аналогичными современным представлениям о том, что совершенная над телом работа переходит в его внутреннюю энергию, то есть теплоту. Также в дневниках Карно пишет[29]:
По некоторым представлениям, которые у меня сложились относительно теории тепла, создание единицы движущей силы требует затраты 2,7 единицы тепла
Однако, ему не удалось найти более точное количественное соотношение между совершенной работой и выделившимся теплом.
Количественное доказательство закона было дано Джеймсом Джоулем в ряде классических опытов. Он помещал в сосуд с водой соленоид с железным сердечником, вращающийся в поле электромагнита. Джоуль измерял количество теплоты, выделявшееся в результате трения в катушке, в случаях замкнутой и разомкнутой обмотки электромагнита. Сравнивая эти величины он пришел к выводу, что выделяемое количество теплоты пропорционально квадрату силы тока и создается механическими силами. Далее Джоуль усовершенствовал установку, заменив вращение катушки рукой на вращение, производимое падающим грузом. Это позволило связать величину выделяемого тепла с изменением энергии груза[22][30]:
количество теплоты, которое в состоянии нагреть 1 фунт воды на 1 градус по Фаренгейту, равно и может быть превращено в механическую силу, которая в состоянии поднять 838 фунтов на вертикальную высоту в 1 фут
Эти результаты были изложены на физико-математической секции Британской ассоциации в его работе 1843 года «О тепловом эффекте магнитоэлектричества и механическом значении тепла»[31].
В работах 1847—1850 годов Джоуль дает еще более точный механический эквивалент тепла. Им использовался металлический калориметр, установленный на деревянной скамье. Внутри калориметра находилась ось с расположенными на ней лопастями. На боковых стенках калориметра располагались ряды пластинок, препятствовавшие движению воды, но не задевавшие лопасти. На ось снаружи калориметра наматывалась нить с двумя свисающими концами, к которым были прикреплены грузы. В экспериментах измерялось количество теплоты, выделяемое при вращении оси из-за трения. Это количество теплоты сравнивалось с изменением положения грузов и силой, действующей на них.
Первым осознал и сформулировал всеобщность закона сохранения энергии немецкий врач Роберт Майер[22]. При исследовании законов функционирования человека у него возник вопрос, не изменится ли количество теплоты, выделяемое организмом при переработке пищи, если он при этом будет совершать работу. Если количество теплоты не изменялось бы, то из того же количества пищи можно было бы получать больше тепла путем перевода работы в тепло (например, через трение). Если же количество теплоты изменяется, то, следовательно, работа и тепло должны быть как-то связаны между собой и с процессом переработки пищи. Подобные рассуждения привели Майера к формулированию закона сохранения энергии в качественной форме[26]:
Движение, теплота, и, как мы намерены показать в дальнейшем, электричество представляют собой явления, которые могут быть сведены к единой силе, которые изменяются друг другом и переходят друг в друга по определенным законам
Ему же принадлежит обобщение закона сохранения энергии на астрономические тела. Майер утверждает, что тепло, которое поступает на Землю от Солнца, должна сопровождаться химическими превращениями или механической работой на Солнце:
Всеобщий закон природы, не допускающий никаких исключений, гласит, что для образования тепла необходима известная затрата. Эту затрату, как бы разнообразна она ни была, всегда можно свести к двум главным категориям, а именно, она сводится либо к химическому материалу, либо к механической работе
Свои мысли Майер изложил в работе 1841 года «О количественном и качественном определении сил»[32], которую послал сначала в ведущий на тот момент журнал «Annalen der Physik und Chemie», где она была отклонена главным редактором журнала Иоганном Поггендорфом, после чего статья была опубликована в «Annalen der Chemie und Pharmacie» (англ.)русск., где оставалась незамеченной до 1862 года, когда ее обнаружил Клаузиус.
Рассуждения Майера и опыты Джоуля доказали эквивалентность механической работы и теплоты, показав, что количество выделяемой теплоты равно совершенной работе и наоборот, однако, формулировку в точных терминах закону сохранения энергии первым дал Герман Гельмгольц[26]. В отличие от своих предшественников, Гельмгольц связывал закон сохранения энергии с невозможностью существования вечных двигателей[33]. В своих рассуждениях он шел от механистической концепции устройства материи, представляя ее как совокупность большого количество материальных точек, взаимодействующих между собой посредством центральных сил. Исходя из такой модели, Гельмгольц свел все виды сил (позднее получивших название видов энергии) к двум большим типам: живым силам движущихся тел (кинетической энергии в современном понимании) и силам напряжения (потенциальной энергии). Закон сохранения этих сил был им сформулирован в следующем виде[34]:
Во всех случаях, когда происходит движение подвижных материальных точек под действием сил притяжения и отталкивания, величина которых зависит только от расстояния между точками, уменьшение силы напряжения всегда равно увеличению живой силы, и наоборот, увеличение первой приводит к уменьшению второй. Таким образом, всегда сумма живой силы и силы напряжения постоянна.
В этой цитате под живой силой Гельмгольц понимает кинетическую энергию материальных точек, а под силой напряжения — потенциальную. Мерой произведенной работы Гельмгольц предложил считать половину величины mq² (где m — масса точки, q — ее скорость) и выразил сформулированный закон в следующей математической форме[34]:
понимая под 
и 
скорости тела в положениях 
и 
соответственно, а под 
— «величину силы, которая действует по направлению r» и «считается положительной, если имеется притяжение, и отрицательной, если наблюдается отталкивание…»[33] Таким образом, главным нововведением Гельмгольца стало введение понятия потенциальных сил и потенциальной энергии, что позволило в дальнейшем обобщить закон сохранения энергии на все разделы физики. В частности, опираясь на закон сохранения энергии, он вывел закон электромагнитной индукции Фарадея.
Переход от понятия «живой силы» к понятию «энергии» произошел в начале второй половине XIX века и был связан с тем, что понятие силы уже было занято в ньютоновской механике. Само понятие энергии в этом смысле было введено еще в 1807 году Томасом Юнгом в его «Курсе лекций по естественной философии и механическому искусству» (англ. «A course of lectures on natural philosophy and the mechanical arts»)[35][36]. Первое строгое определение энергии дал Уильям Томсон в 1852 году в работе «Динамическая теория тепла»[26][37]:
Под энергией материальной системы в определенном состоянии мы понимаем измеренную в механических единицах работы сумму всех действий, которые производятся вне системы, когда она переходит из этого состояния любым способом в произвольно выбранное нулевое состояние
Открытие закона сохранения энергии оказало влияние не только на развитие физических наук, но и на философию XIX века.
С именем Роберта Майера связано возникновение так называемого естественнонаучного энергетизма — мировоззрения, сводящего все существующее и происходящее к энергии, ее движению и взаимопревращению. В частности, материя и дух в этом представлении являются формами проявления энергии. Главным представителем этого направления энергетизма является немецкий химик Вильгельм Оствальд, высшим императивом философии которого стал лозунг «Не растрачивай понапрасну никакую энергию, используй ее!»
С точки зрения диалектического материализма, закон сохранения энергии, как и другие законы сохранения, является естественнонаучным обоснованием положения о единстве природы, поскольку он указывает на закономерный характер превращения одних форм движения в другие, раскрывает глубокую внутреннюю связь, существующую между всеми формами движения
Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про закон сохранения Надеюсь, что теперь ты понял что такое закон сохранения, превращения энергии, теорема кёнига и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Физические основы механики
Комментарии
Оставить комментарий
Физические основы механики
Термины: Физические основы механики