Роботы-манипуляторы. Манипуляторы

Сразу хочу сказать, что здесь никакой воды про роботы-манипуляторы, и только нужная информация. Для того чтобы лучше понимать что такое роботы-манипуляторы, манипуляторы , настоятельно рекомендую прочитать все из категории Робототехника.

  роботы- манипуляторы . 

Использование манипуляторов стало обыденным явлением еще в 20-м веке. На сегодняшний день ни одно крупное промышленное про- изводство не обходится без них. Кроме того, манипуляторы устанавли- вают и на мобильных роботах, чтобы расширить возможности управле- ния в труднодоступных для человека местах. При однообразных и мо- нотонных действиях робот также может заменить человека, например раскладывать пирожные по коробочкам. Итак, определим манипулятор как управляемое устройство, пред- назначенное для выполнения сложных действий, аналогичных движе- ниям руки человека. В том числе, это механизм для управления поло- жением предметов.

Стрела манипулятора
Для освоения управления манипулятором следует вернуться к контролю положения двигателя с помощью П-регулятора, которое описано
в главе «Алгоритмы управления». Только конструкция будет несколько отличаться от описанной (рис. 8.148-8.149).

Рис. 8.148. Крепление мотора к корпусу NXT горизонтально на уровне по- верхности. Штифт-полуось вствляется в вал мотора снизу.

Рис. 8.149. Первое колено манипулятора.

Стрела манипулятора расположена горизонтально. Алгоритм управления состоит из двух параллельных задач. В первой работает 
П-регулятор, который удерживает мотор в положении alpha. Во второй положение alpha изменяется со временем (рис. 8.150).

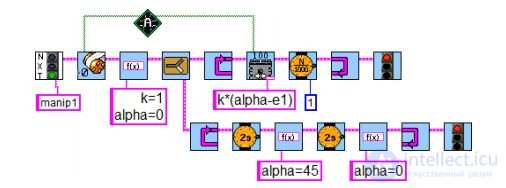
Рис. 8.150. Управление горизонтальным положением стрелы манипулятора.

Учитывая, что нулевое положение определяется на старте, задайте отрицательный угол во второй параллельной задаче и осуществите по-
следовательный переход через нуль. Если все получается, следует приступить к установке второго мотора с захватом.

 Манипулятор с захватом

Рис. 8.151. Установка захвата на второй мотор.

Рис. 8.152. Мотор с захватом закрепляется на диске первого мотора.

Рис. 8.152. Мотор с захватом закрепляется на диске первого мотора.
Программирование робота с двумя степенями свободы (рис. 8.151-8.152) осуществляется аналогично. Новая переменная beta будет
определять положение второго мотора. Расширьте вторую задачу, подобрав подходящие значения для открывания и закрывания захвата
(рис. 8.153). Не забывайте, что стартовое положение определяет все.

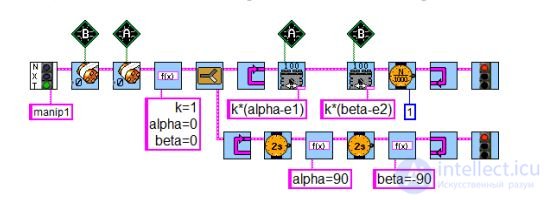
 Рис. 8.153. Заготовка для управления двумя моторами на основе П-регуля- торов. Необходимо продолжить цикл в параллельной задаче.

Точное позиционирование. Дискретный регулятор.

Библиографическое описание: Мусаев Г. М. Моделирование системы позиционирования отражателя концентратора солнечной энергии [Текст] / Г. М. Мусаев // Молодой ученый. — 2013. — №3. — С. 81-83.

Целью создания системы точного углового позиционирования является разработка и изготовление аппаратных и программных средств, необходимых для обеспечения управления с помощью ЭВМ системой позиционирования различных объектов. Об этом говорит сайт https://intellect.icu . В качестве исполнительного устройства используются двигатели постоянного тока с редукторами и датчиками углового перемещения различных типов.

Для решения научно-практических задач требуется обеспечить угловое позиционирование объектов с высокой точностью .

К основным параметрам системы можно отнести:

• Точность определения координат.

• Точность позиционирования.

Системы управления динамическими объектами с цифровыми регуляторами представляют собой достаточно сложный для описания класс. Непрерывная часть системы (объект управления) задается дифференциальными уравнениями, тогда как микропроцессоры, реализующие алгоритмы управляющих устройств, представлены разностными уравнениями. Смешанное описание в виде дифференциальных и разностных уравнений, дополненных соотношениями для преобразователей аналог-код и код-аналог, создает значительные трудности при решении типовых задач анализа и синтеза. Поэтому в практике управления получили распространение модели, которые описывают поведение систем лишь в дискретные (тактовые) моменты времени. При этом удается ограничиться лишь разностными уравнениями, что радикально упрощает описание рассматриваемых систем и решение соответствующих задач синтеза регуляторов.

Альтернативный подход, напротив, предлагает ограничиться исходным описанием системы дифференциальными уравнениями и синтезировать непрерывные регуляторы, которые уже после синтеза реализуются на микропроцессорах. Оба этих подхода широко используются в практике управления, хотя каждый их них имеет свои методические погрешности.

Альтернативный подход к синтезу дискретных регуляторов предлагает решать задачи управления, оставаясь в рамках непрерывных систем. При этом синтезируется непрерывный регулятор, который затем реализуется цифровыми методами. Физически ясно, что поведение дискретной системы будет приближаться к поведению непрерывной с уменьшением периода квантования. Чтобы оценить изменения, вносимые в динамику непрерывных систем применением микропроцессоров, рассмотрим сначала частотные характеристики экстраполятора нулевого порядка

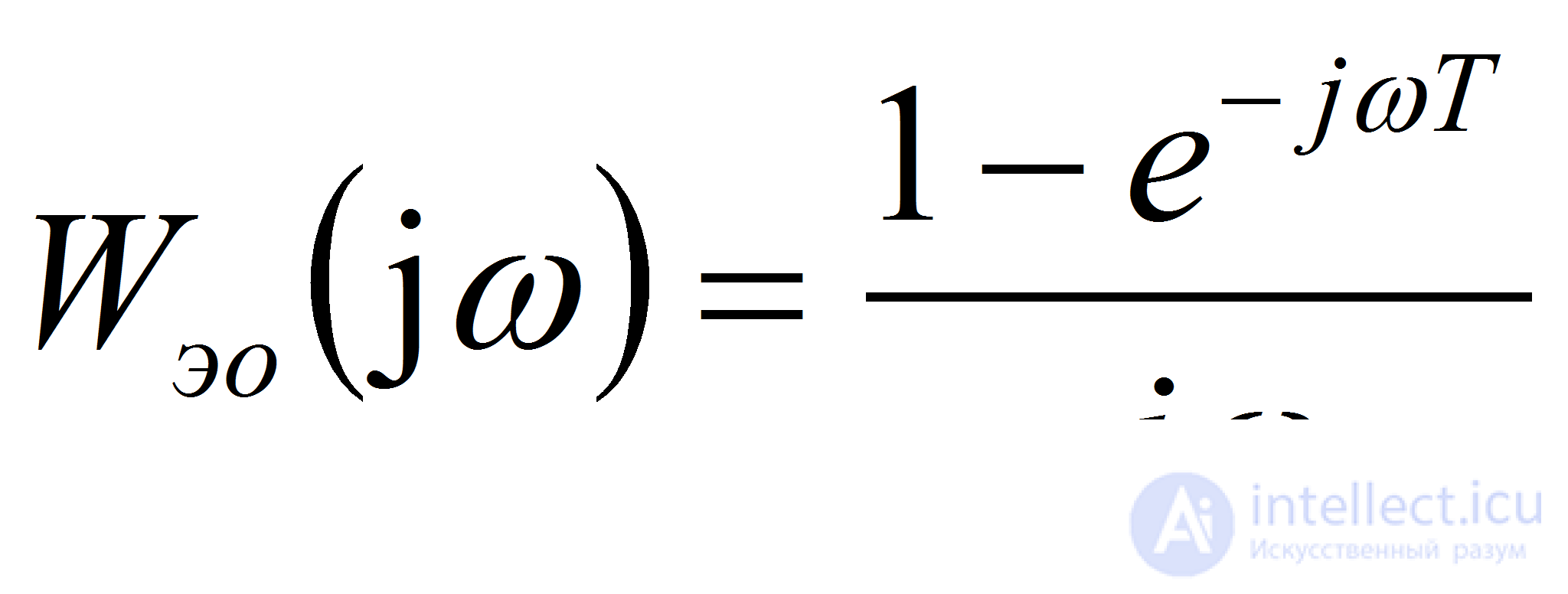 (1)

Заменяя экспоненту тригонометрическими функциями, после простых преобразований найдем

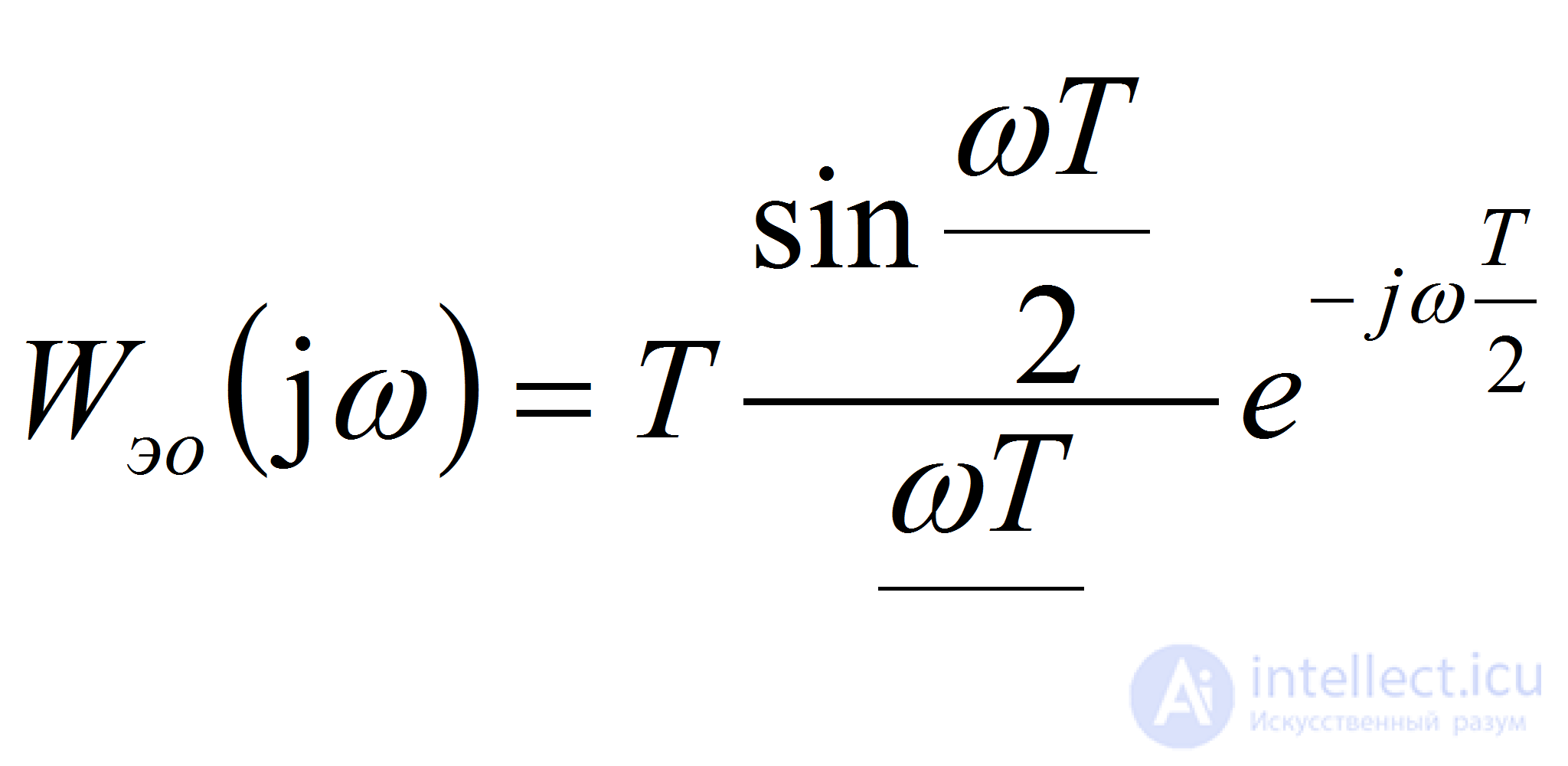 (2)

Из последнего соотношения видно, что коэффициент передачи экстраполятора равен периоду квантования. Экстраполятор создает чистое запаздывание, величина которого равна половине периода квантования. При проектировании частота квантования выбирается существенно большей диапазона рабочих частот системы.

Преобразователи вносят в систему дополнительное запаздывание, равное половине периода квантования. Поэтому синтез регуляторов при их последующей реализации на микропроцессоре следует выполнять для модифицированного объекта, отличающегося от исходного наличием звена чистого запаздывания

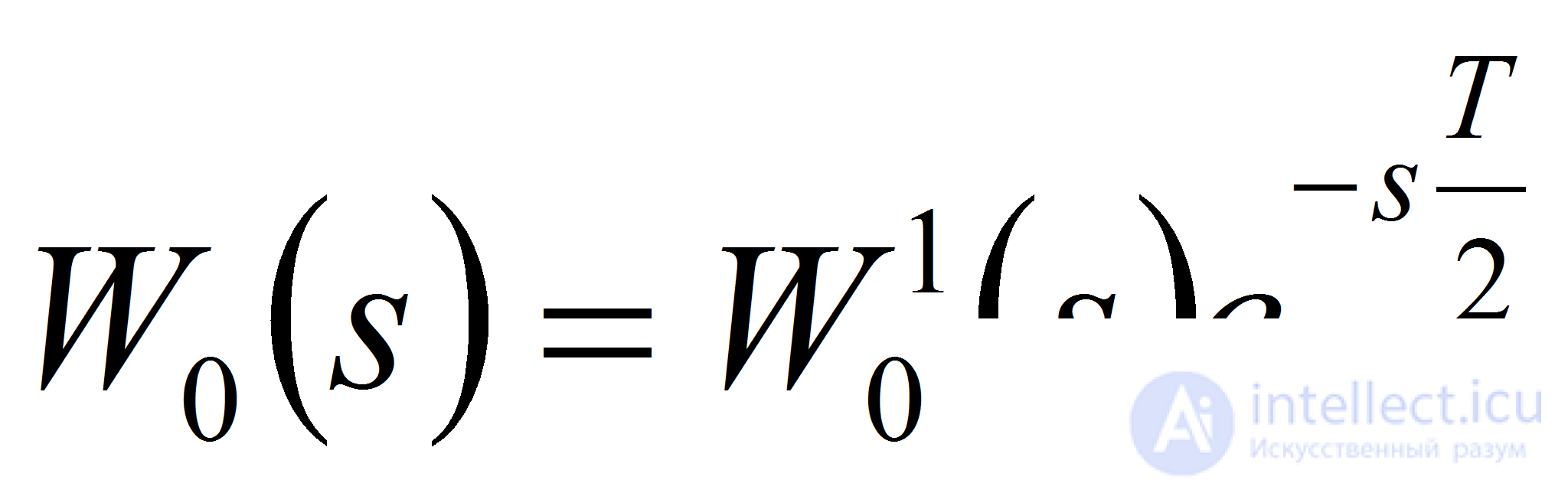 (3)

В качестве системы управления динамическим объектом с цифровыми регуляторами рассмотрим устройство управления двигателем постоянного тока. Двигатели постоянного тока применяют в приводах, требующих плавного регулирования частот вращения в широком диапазоне.

Основным звеном устройства управления двигателем постоянного тока, выполняющим роль преобразователя и источника управляющих сигналов, может быть микроконтроллер (МК).

Свойства двигателей постоянного тока, определяются пусковыми, рабочими, механическими и регулировочными характеристиками.

Индексами «в» и «я» отмечены параметры и переменные цепей возбуждения и якоря; L — индуктивность, R — активное сопротивление, U — напряжение, i — ток; М — электромагнитный момент двигателя, е — ЭДС якоря.

От двигателя, применяемого в следящих системах, требуется преобразование электрического сигнала (управляющего напряжения) в пропорциональную величине сигнала скорость вращения якоря. Как правило, используются двигатели постоянного тока с независимым возбуждением. Принципиальная схема двигателя приведена на рис.1.

Рис. 1. Принципиальная схема двигателя постоянного тока.

Управление двигателем возможно путем изменения напряжений или по цепи якоря U_Я, или по цепи обмотки управления U_B..

Рассмотрим вначале уравнения статики. Ток в цепи якоря /_Я, магнитный поток возбуждения Ф_В, вращающий момент М_вр, скорость вращения вала двигателя ω и противоэлектродвижущая сила е_п,наводимая в обмотке якоря, связаны следующими соотношениями:

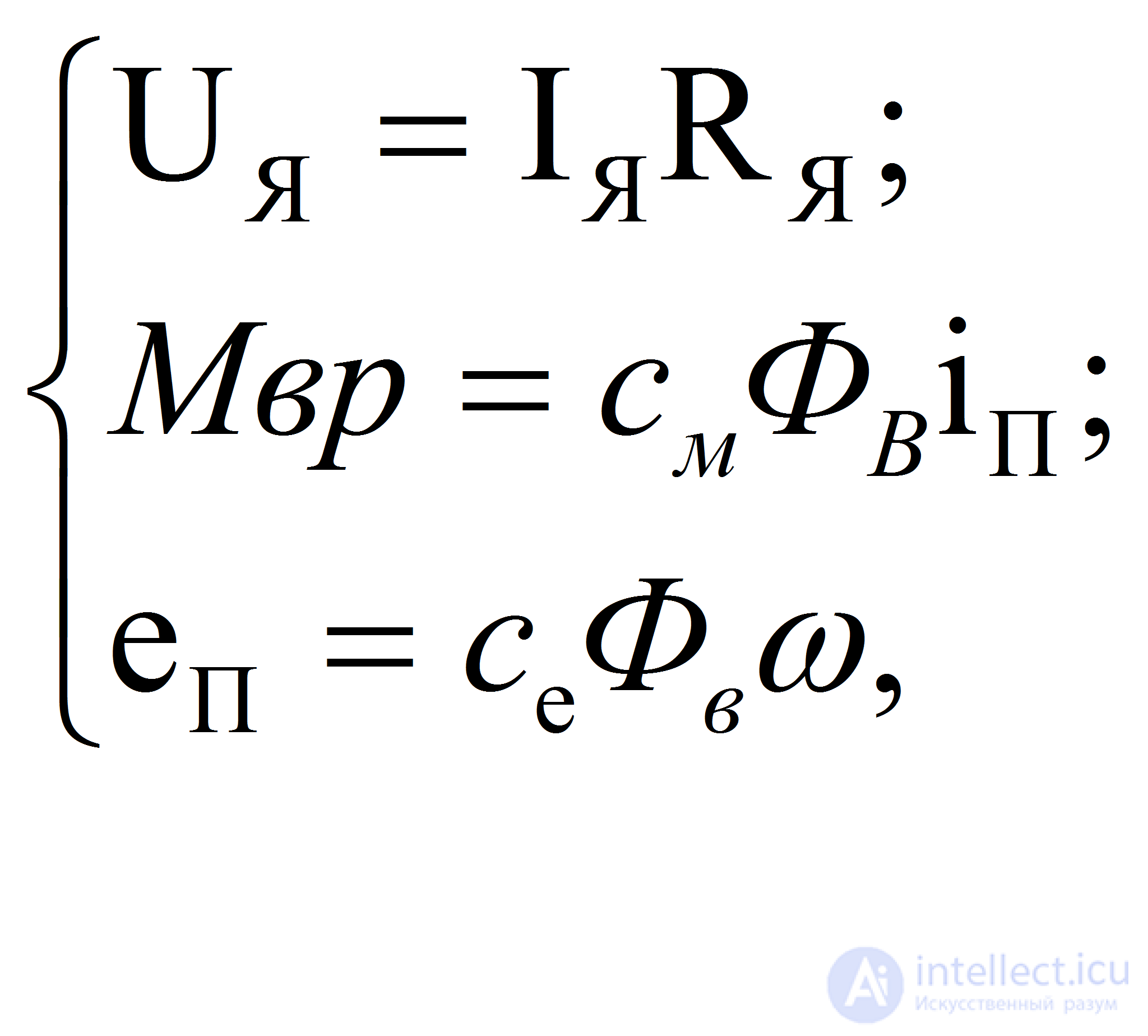 (4)

где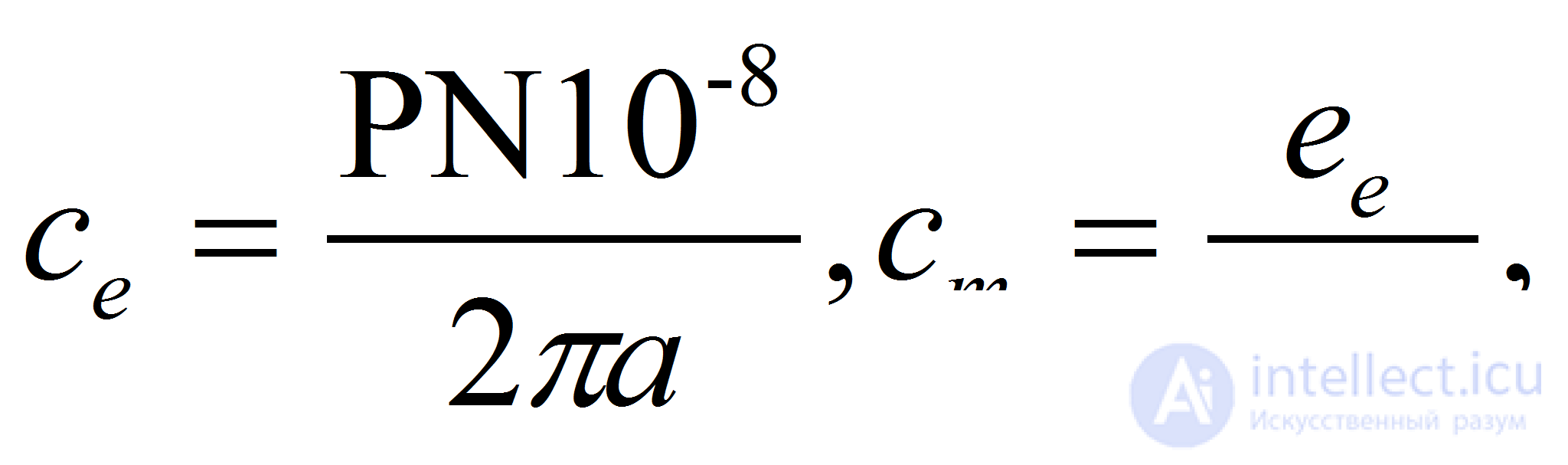 

N — число проводников якоря, Р — число пар полюсов, а — число пар параллельных ветвей, R_я — активное сопротивление цепи якоря. Исключая из уравнения е_п и i_я получим

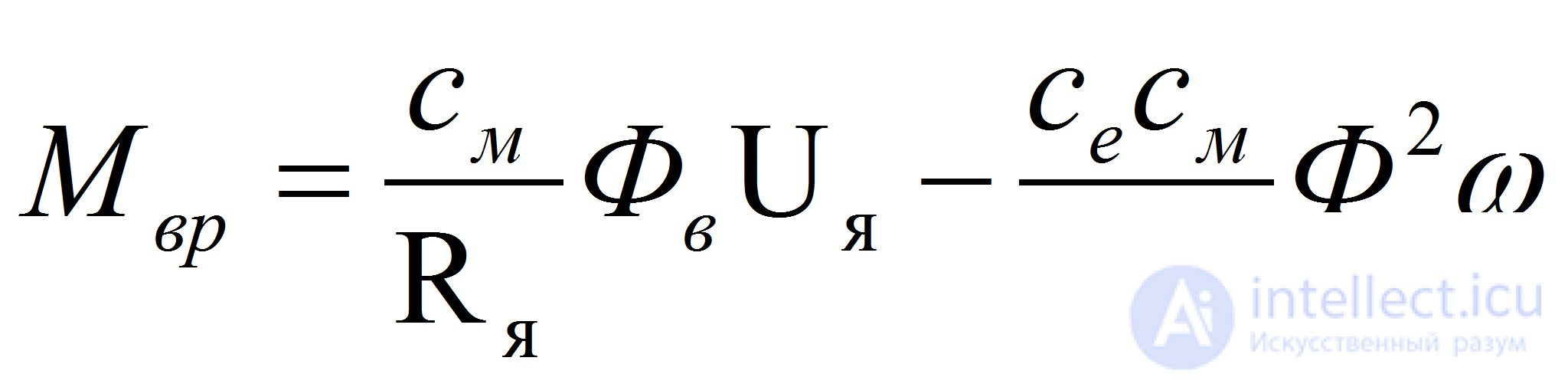 (5)

Из формулы (4), которая определяет механическую характеристику двигателя, видно, что при постоянном потоке возбуждения Ф_в, создаваемом неизменяемым напряжением возбуждения U_в,вращающий момент линейно зависит от управляющего сигнала по цепи якоря U_я. Это позволяет плавно изменять скорость двигателя в широком диапазоне. В связи с этим обстоятельством в рассматриваемой следящей системе управление двигателем осуществляется именно по цепи якоря. Составим уравнение динамики для двигателя постоянного тока, управляемого по цепи якоря.

Уравнение движения якоря двигателя имеет вид

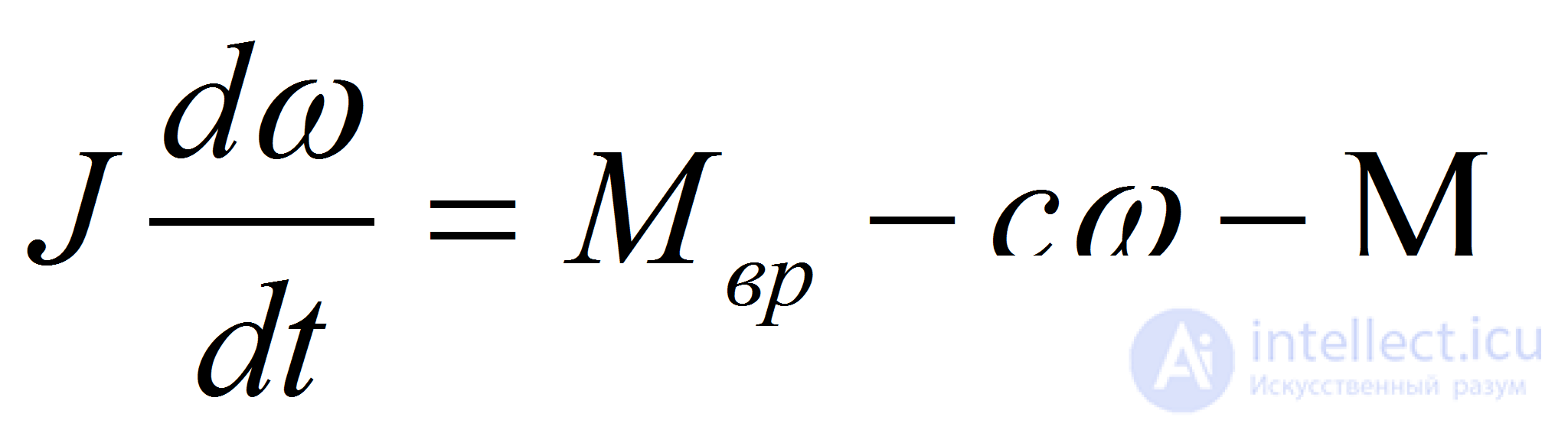 (6)

Здесь J — момент инерции всех вращающихся масс, приведенных к валу двигателя, с —коэффициент вязкого трения, М_с — момент сопротивления.

Из (5) и (6) получим

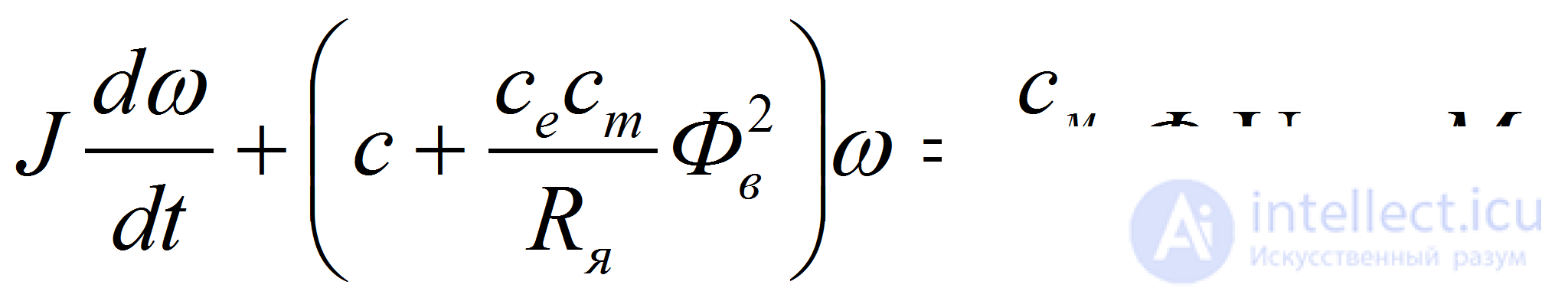
или

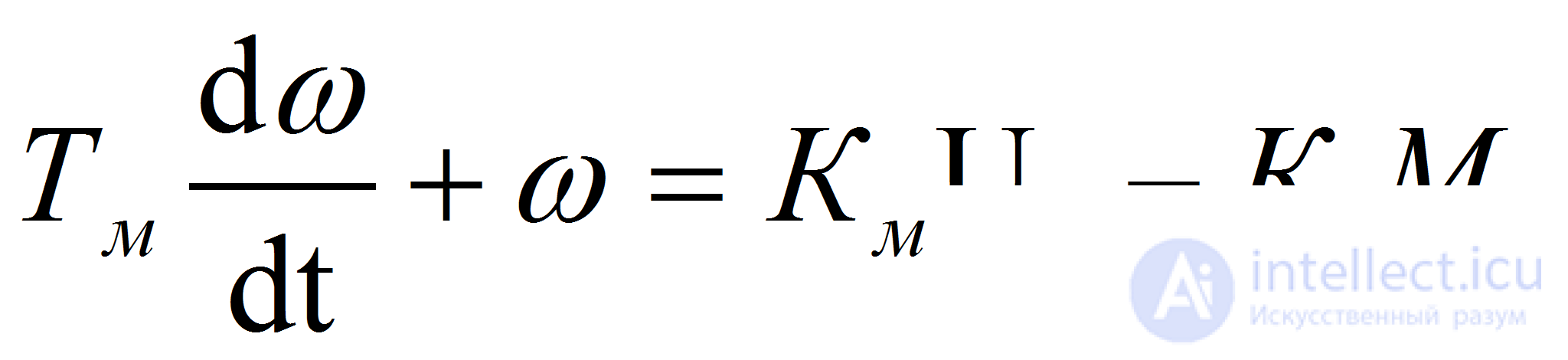 (7)

где Т_м — постоянная времени двигателя, К_м — коэффициент передачи двигателя по управлению, К_с— коэффициент передачи двигателя по возмущению:

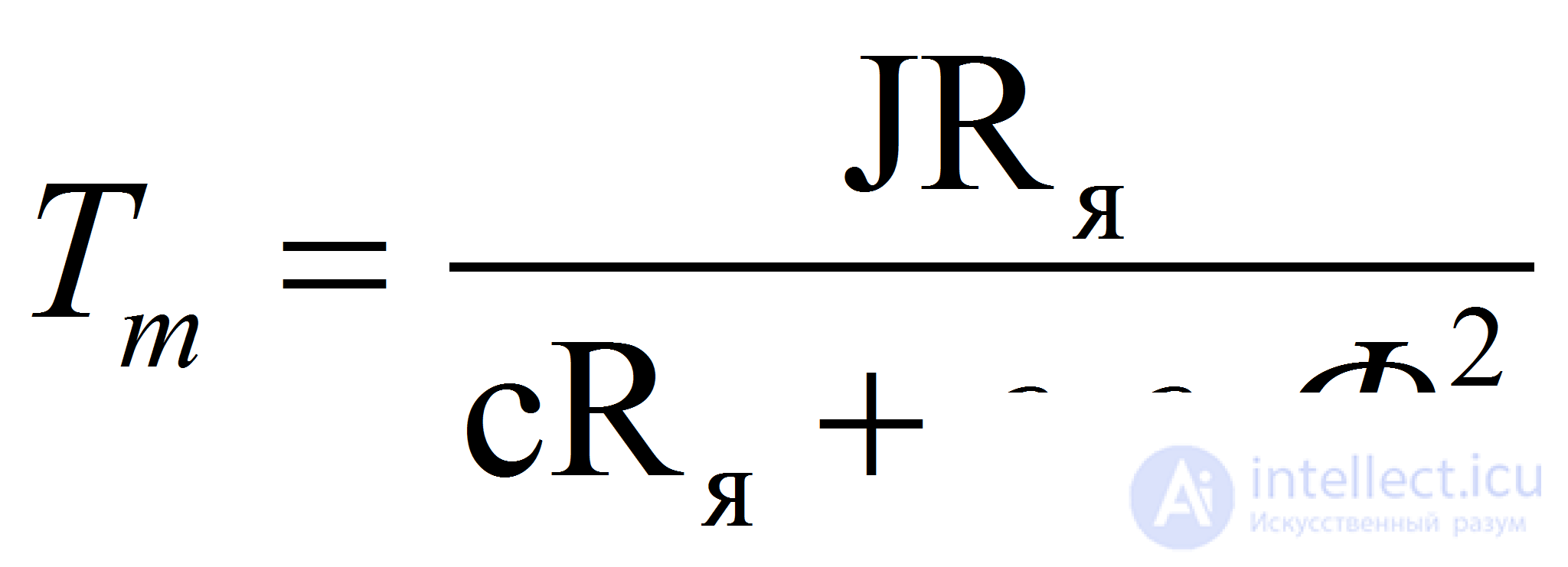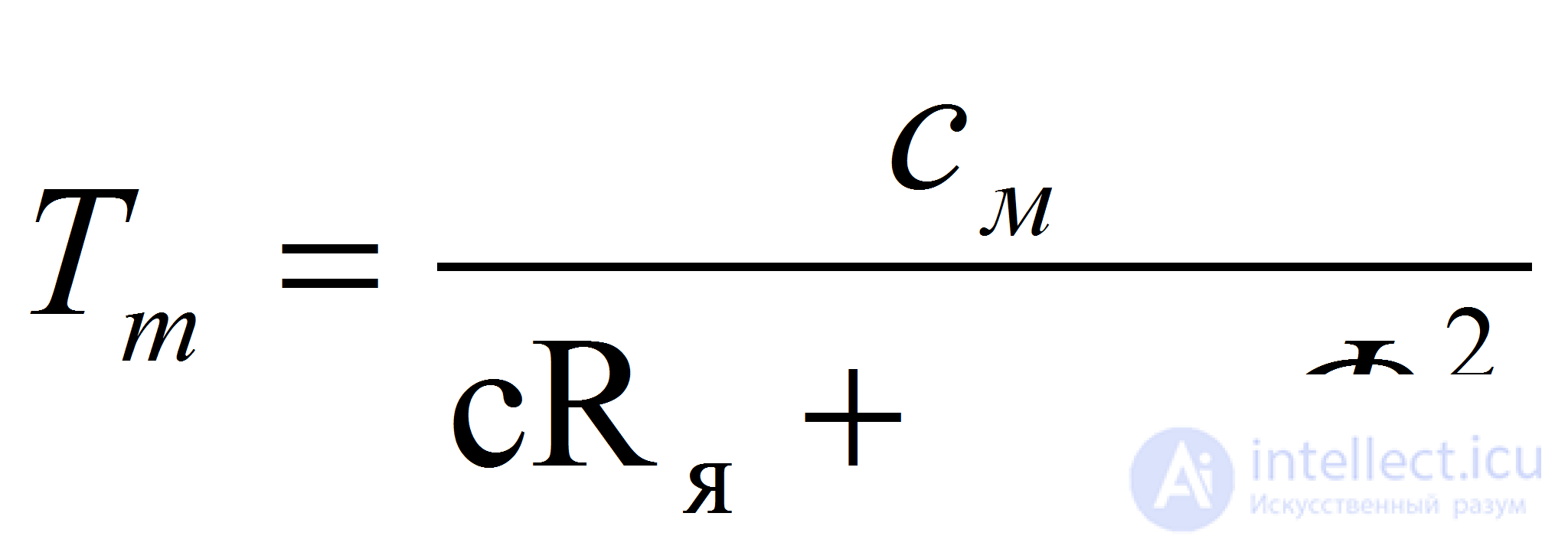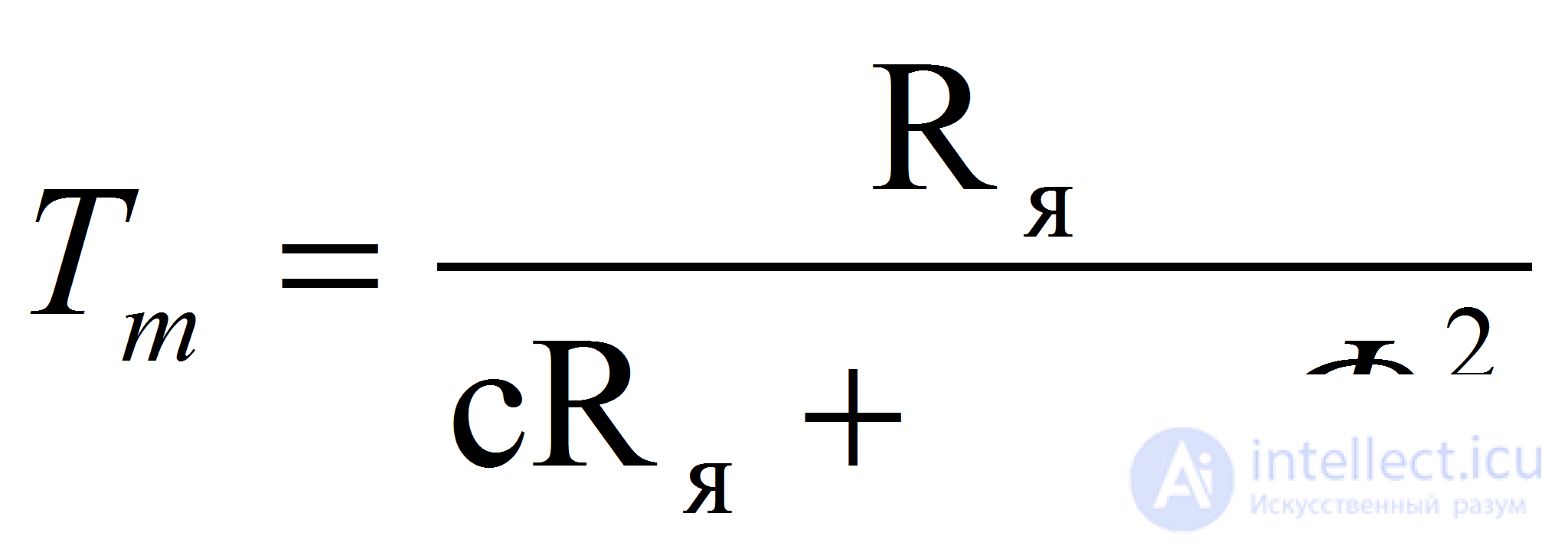; ;  (8)

Соответственно передаточные функции двигателя по управлению и возмущению (моменту сопротивления) относительно угловой скорости имеют вид

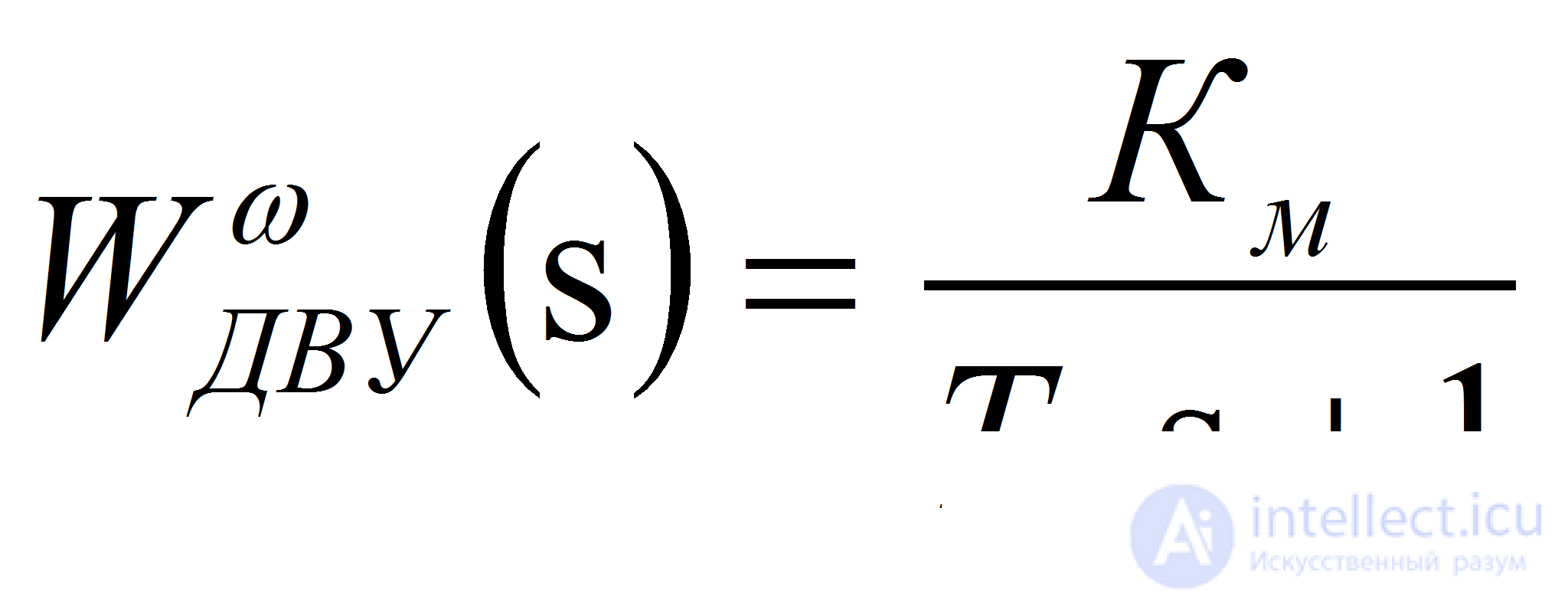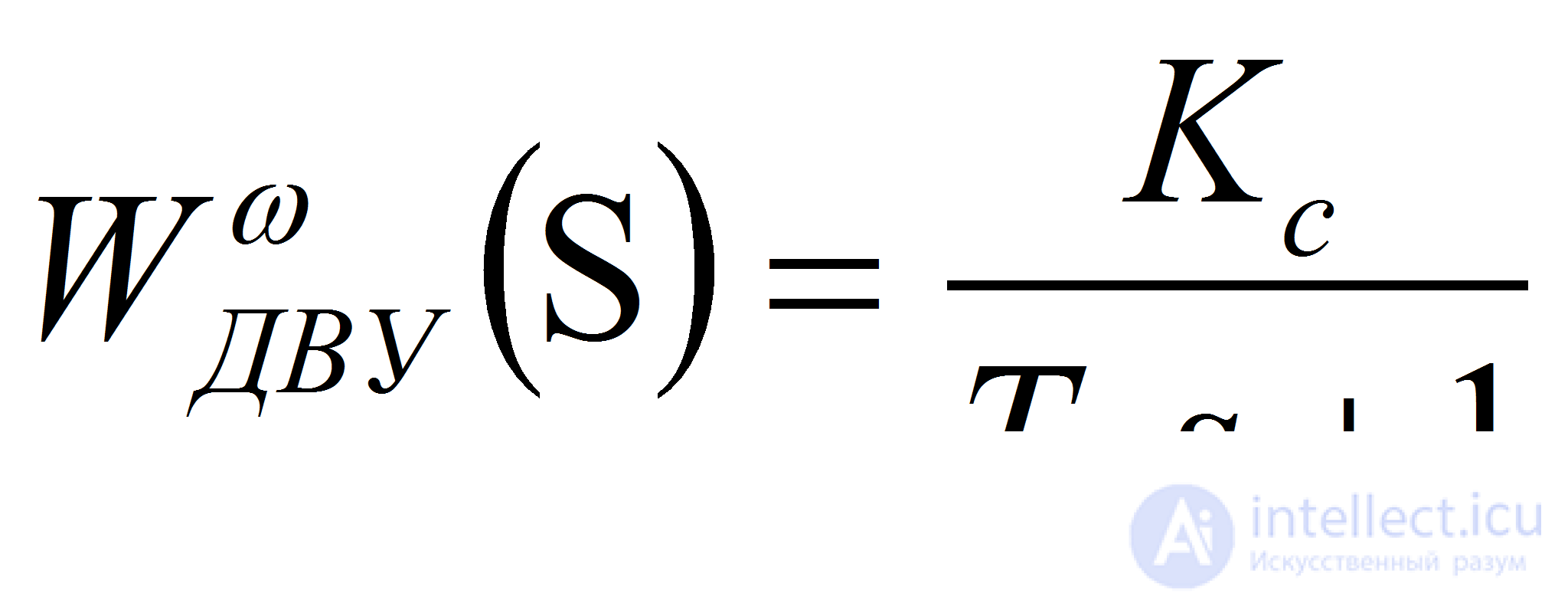;  (9)

Уравнение (7) можно записать относительно угла поворота. Учитывая, что 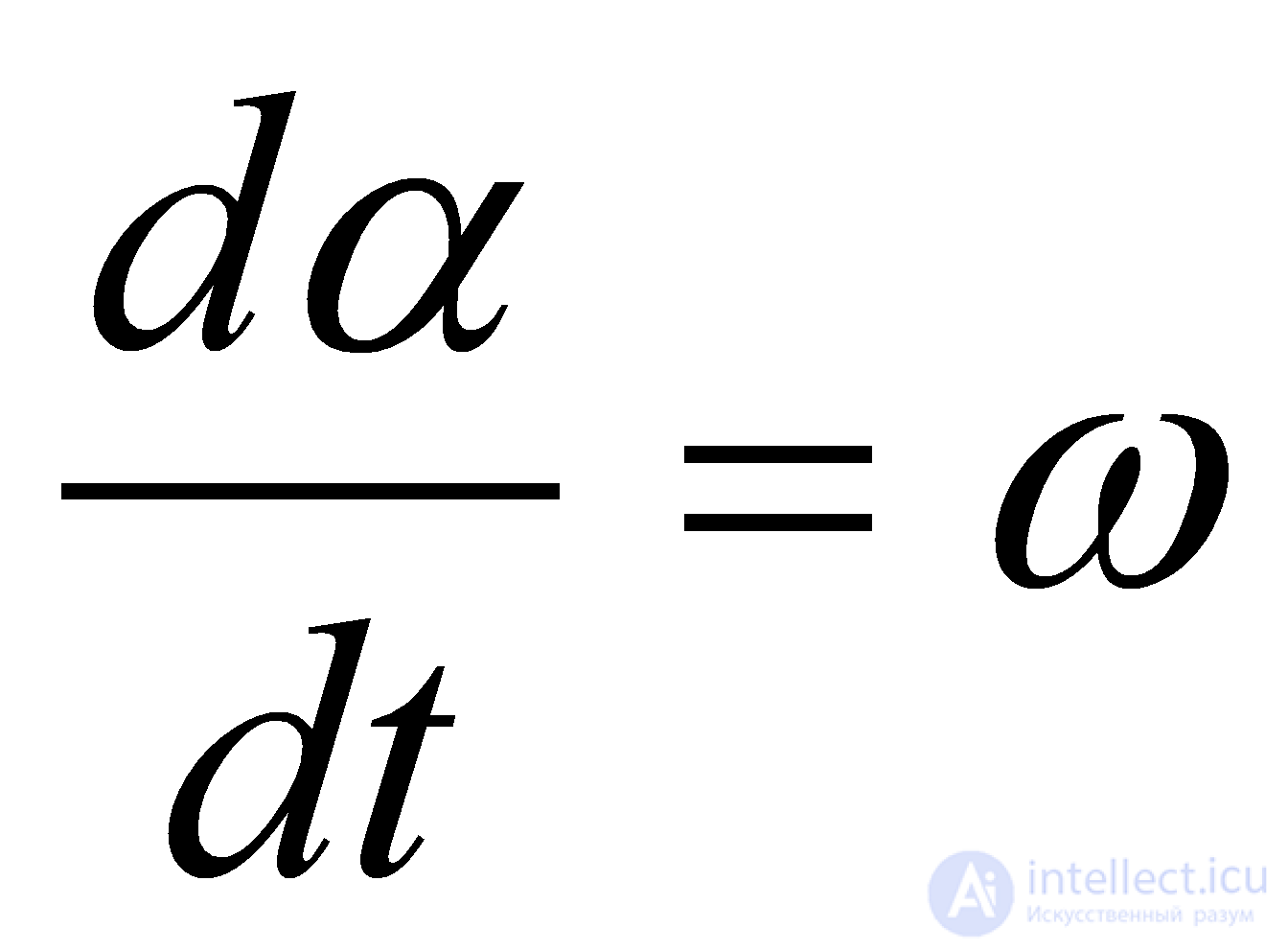 получаем следующее уравнение:

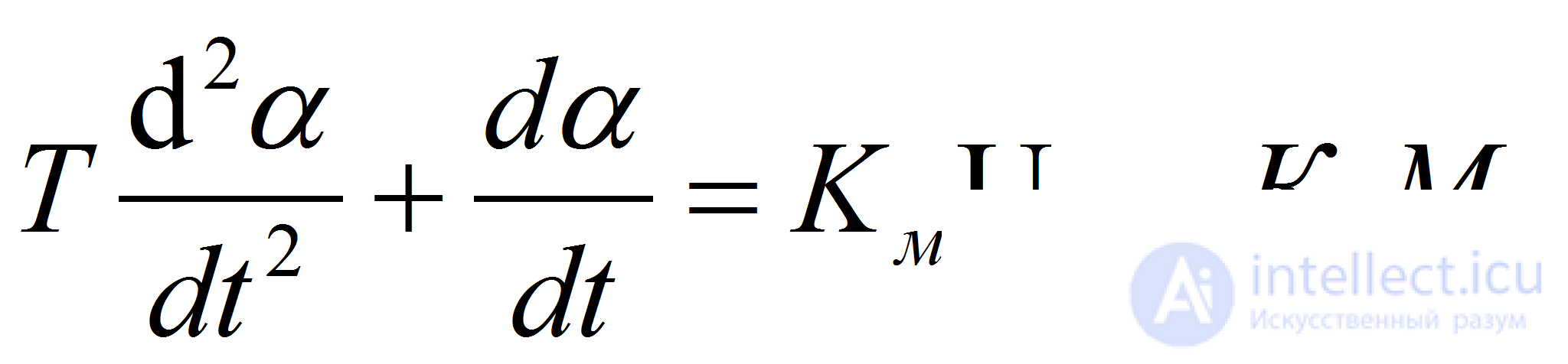 (10)

Двигателю, описываемому уравнением (11), соответствуют две передаточные функции — по управлению и по возмущению относительно угла поворота:

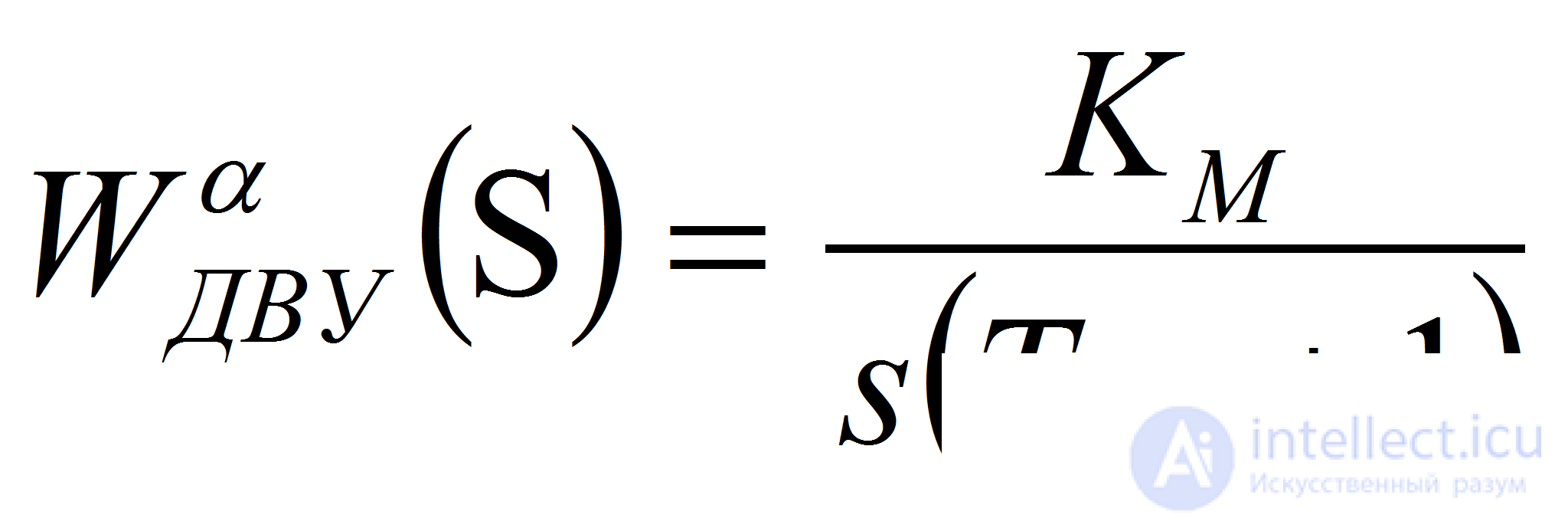 (11)

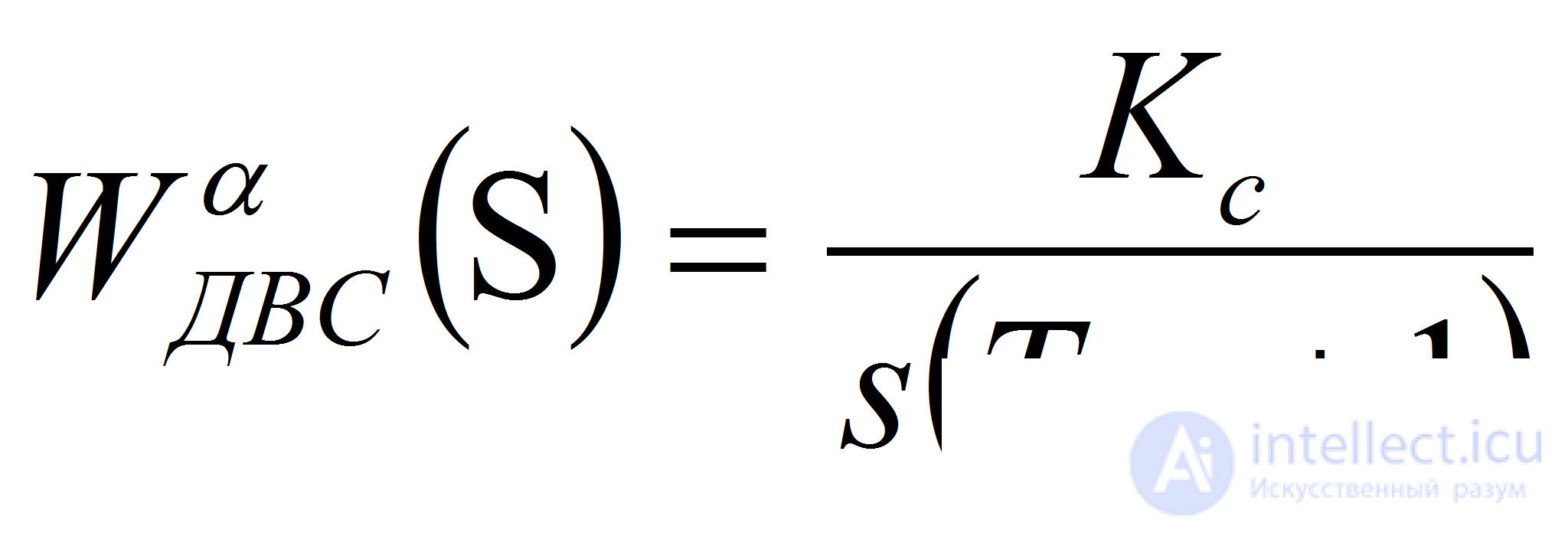 (12)

А как ты думаешь, при улучшении роботы-манипуляторы, будет лучше нам? Надеюсь, что теперь ты понял что такое роботы-манипуляторы, манипуляторы и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Робототехника