Локализация как пример робототехнического восприятия

Привет, мой друг, тебе интересно узнать все про локализация у роботов, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое локализация у роботов , настоятельно рекомендую прочитать все из категории Робототехника.

Локализация— это универсальный пример робототехнического восприятия. Она представляет собой задачу определения того, где что находится. Локализация — одна из наиболее распространенных задач восприятия в робототехнике, поскольку знания о местонахождении объектов и самого действующего субъекта являются основой любого успешного физического взаимодействия. Например, роботы, относящиеся к типу манипуляторов, должны иметь информацию о местонахождении объектов, которыми они манипулируют. А роботы, передвигающиеся в пространстве, должны определять, где находятся они сами, чтобы прокладывать путь к целевым местонахождениям.

Существуют три разновидности задачи локализации с возрастающей сложностью. Если первоначальная поза локализуемого объекта известна, то локализация сводится к задаче отслеживания траектории. Задачи отслеживания траектории характеризуются ограниченной неопределенностью. Более сложной является задачаглобальной локализации, в которой первоначальное местонахождение объекта полностью неизвестно. Задачи глобальной локализации преобразуются в задачи отслеживания траектории сразу после локализации искомого объекта, но в процессе их решения возникают также такие этапы, когда роботу приходится учитывать очень широкий перечень неопределенных состояний. Наконец, обстоятельства могут сыграть с роботом злую шутку и произойдет "похищение" (т.е. внезапное исчезновение) объекта, который он пытался локализовать. Задача локализации в таких неопределенных обстоятельствах называется задачей похищения. Ситуация похищения часто используется для проверки надежности метода локализации в крайне неблагоприятных условиях.

В целях упрощения предположим, что робот медленно движется на плоскости и что ему дана точная карта среды. Поза такого мобильного робота определяется двумя декартовыми координатами со значениями х и у, а также его угловым направлением со значением 0, как показано на рисунке а). (Обратите внимание на то, что исключены соответствующие скорости,

поэтому рассматриваемая модель скорее является кинематической, а не  динамической.) Если эти три значения будут упорядочены в виде вектора, то любое конкретное состояние определится с помощью соотношения xt= (x_t, y_t, 0_t)^т.

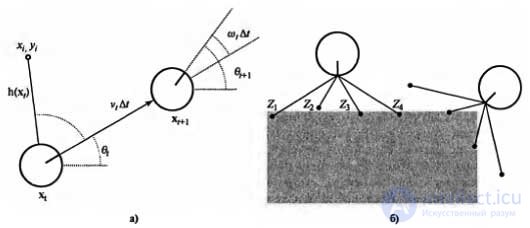
Пример применения карты среды: упрощенная кинематическая модель мобильного робота. Робот показан в виде кружка с отметкой, обозначающей переднее направление. Показаны значения позиции и ориентации в моменты времени t и t+1, а обновления обозначены соответственно термами v_t∆_t и w_t∆_t. Кроме того, приведена отметка с координатой (x_i,y_i), наблюдаемая во время t(а); модель датчика расстояния. Показаны две позы робота, соответствующие заданным результатам измерения расстояний (z_1, z₂, z₃, z₄). Гораздо более вероятным является предположение, что эти результаты измерения расстояний получены в позе, показанной слева, а не справа (б)

В этой кинематической аппроксимации каждое действие состоит из "мгновенной" спецификации двух скоростей — скорости переноса v_t и скорости вращения w_t. Для небольших временных интервалов ∆_t грубая детерминированная модель движения таких роботов задается следующим образом:

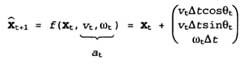
Обозначение x относится к детерминированному предсказанию состояния. Безусловно, поведение физических роботов является довольно непредсказуемым. Такая ситуация обычно моделируется гауссовым распределением со средним f (x_t, v_t, w_t) и ковариацией ∑_x..

P(x_t+1 | x_t, w_t) = N(x_t+1, ∑_x)

Затем необходимо разработать модель восприятия. Об этом говорит сайт https://intellect.icu . Рассмотрим модели восприятия двух типов. В первой из них предполагается, что датчики обнаруживают стабильные, различимые характеристики среды, называемые  отметками. Для каждой отметки они сообщают дальность и азимут. Предположим, что состояние робота определяется выражением x_t= (x_t,y_t,0_t)^T и он принимает информацию об отметке, местонахождение которой, как известно, определяется  координатами (x_i,y_i)^Т. При отсутствии шума дальность и азимут можно вычислить с помощью простого геометрического соотношения. Точное предсказание наблюдаемых значений дальности и азимута может быть выполнено с помощью следующей формулы:

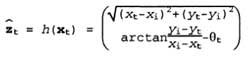
Еще раз отметим, что полученные результаты измерений искажены шумом. Для упрощения можно предположить наличие гауссова шума с ковариацией ∑_z:

P(z_t | x_t) = N(z_t,∑_z)

Для дальномеров, часто более приемлемой является немного другая модель восприятия. Такие датчики вырабатывают вектор значений дальности z_t = (z₁,...., z_M)^т, в каждом из которых азимуты являются фиксированными по отношению к роботу. При условии, что дана поза x_t, допустим, что

z_j — точное расстояние вдоль направления j-ro луча от x_t до ближайшего препятствия. Как и в описанном раньше случае, эти результаты могут быть искажены гауссовым шумом. Как правило, предполагается, что погрешности для различных направлений лучей независимы и заданы в виде идентичных распределений, поэтому имеет место следующая формула:

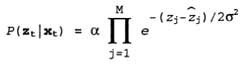
На рисунке б) показан пример четырехлучевого дальномера и двух возможных поз робота, одну из которых на полном основании можно рассматривать как позу, в которой были получены рассматриваемые результаты измерения дальностей, а другую — нет. Сравнивая модель измерения дальностей с моделью отметок, можно убедиться в том, что модель измерения дальностей обладает преимуществом в том, что не требует идентификации отметки для получения возможности интерпретировать результаты измерения дальностей; и действительно, как показано на рисунке б), робот направлен в сторону стены, не имеющей характерных   особенностей. С другой стороны, если бы перед ним была видимая, четко идентифицируемая отметка, то робот мог бы обеспечить немедленную локализацию. Описан фильтр Калмана, позволяющий представить доверительное состояние в виде одного многомерного гауссова распределения, и фильтр частиц, который представляет доверительное состояние в виде коллекций частиц, соответствующих состоянию. В большинстве современных алгоритмов локализации используется одно из этих двух представлений доверительного состояния робота, Р(x_t | z_1:t, a_1:t-1).

Локализация с использованием фильтрации частиц называется локализацией Монте-Карло, или сокращенно MCL (Monte Carlo Localization). Алгоритм MCL идентичен алгоритму фильтрации частиц, приведенному в листинге ; достаточно лишь предоставить подходящую модель движения и модель восприятия. Одна из версий алгоритма, в которой используется модель измерения дальностей, приведена в листинге. Работа этого алгоритма продемонстрирована на рисунке ниже, где показано, как робот определяет свое местонахождение в офисном здании. На первом изображении частицы распределены равномерно согласно распределению априорных вероятностей, показывающему наличие глобальной неопределенности в отношении положения робота. На втором изображении показано, как поступает первый ряд результатов измерений и частицы формируют кластеры в областях с высоким распределением апостериорных доверительных состояний. А на третьем  изображении показано, что поступило достаточное количество результатов измерений, чтобы переместить все частицы в одно место.

Листинг. Алгоритм локализации Монте-Карло, в котором используется модель восприятия результатов измерения дальностей с учетом наличия независимого шума

Еще один важный способ локализации основан на применении фильтра Калмана. Фильтр Калмана представляет апостериорную вероятность P(x_t | z_1:t, a_1:t-1) с помощью гауссова распределения. Среднее этого гауссова распределения будет обозначено µ_t, а его ковариация — ∑_t. Основным недостатком использования гауссовых доверительных состояний является то, что они замкнуты только при использовании линейных моделей движения f и линейных моделей измерения h. В случае нелинейных f или h результат обновления фильтра обычно не является гауссовым. Таким образом, алгоритмы локализации, в которых используется фильтр Калмана,  линеаризуют модели движения и восприятия. Линеаризацией называется локальная аппроксимация нелинейной функции с помощью линейной.

Метод локализации Монте-Карло, основанный на применении алгоритма фильтрации частиц для локализации мобильного робота: первоначальное состояние, глобальная неопределенность (а); приблизительно бимодальное состояние неопределенности после прохождения по (симметричному) коридору (б); унимодальное состояние неопределенности после перехода в офис, отличимый от других (в)

На рисунке 1  показано применение понятия линеаризации для (одномерной) модели движения робота. В левой части показана нелинейная модель движения f(x_t,a_t) (параметр a_t на этом графике не показан, поскольку он не играет никакой роли в этой линеаризации). В правой части эта функция аппроксимируется линейной функцией f(x_t, a_t). График этой линейной функции проходит по касательной к кривой f в точке µ_t, которая определяет среднюю оценки состояния во время t. Такая линеаризация называется  разложением в ряд Тейлора (первой степени). Фильтр Калмана, линеаризующий функции f и h с помощью разложения в ряд Тейлора, называетсярасширенным фильтром Калмана (или Extended Kalman Filter— EKF). На рисунке 2 показана последовательность оценок, полученных роботом, который действует под управлением алгоритма локализации на основе расширенного фильтра Калмана. По мере передвижения робота неопределенность в оценке его местонахождения возрастает, как показано с помощью эллипсов погрешностей. Но как только робот начинает получать данные о дальности и азимуте до отметки с известным местонахождением, его погрешность уменьшается. Наконец, погрешность снова возрастает, как только робот теряет отметку из виду. Алгоритмы EKF действуют успешно, если отметки являются легко идентифицируемыми. Еще один вариант состоит в том, что распределение апостериорных вероятностей может быть мультимодальным. Задача, для решения которой требуется знать идентификацию отметок, представляет собой пример задачи ассоциации данных.

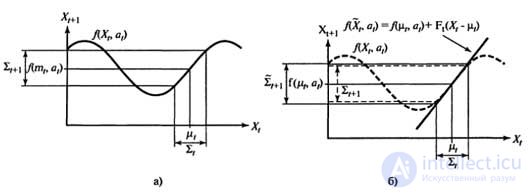
Рисунок 1. Одномерная иллюстрация линеаризованной модели движения: функция f, проекция среднего µ_t и интервал ковариации (основанный на ∑_t) во время t+1 (а); линеаризованная версия представляет собой касательную к кривой функции f при значении µ_t. Проекция среднего µ_t  определена правильно. Однако проекция ковариации ∑_t+1 отличается от ∑_t+1 (б)

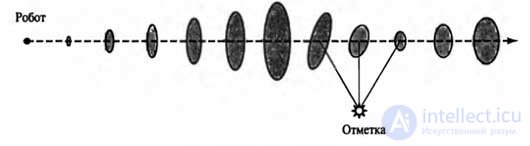
Рисунок 2.  Пример локализации с использованием расширенного фильтра Калмана. Робот движется по прямой. По мере его продвижения неопределенность постепенно возрастает, как показано с помощью эллипсов погрешностей. А после обнаружения роботом отметки с известной позицией неопределенность уменьшается.

Если я не полностью рассказал про локализация у роботов? Напиши в комментариях Надеюсь, что теперь ты понял что такое локализация у роботов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Робототехника