Привет, сегодня поговорим про рекурсивные структуры данных, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
рекурсивные структуры данных , настоятельно рекомендую прочитать все из категории Структуры данных.
Рассмотрим рекурсивные алгоритмы и
рекурсивные структуры данных .
Рекурсия - процесс, протекание которого связано с обращением к самому себе (к этому же процессу).
Пример рекурсивной структуры данных - структура данных, элементы которой являются такими же структурами данных (рис. 4.1).
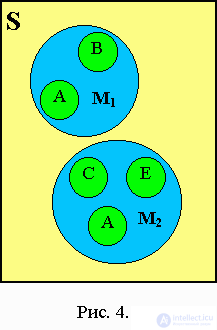
4.1 Деревья
Дерево - нелинейная связанная структура данных
(рис. 4.2).
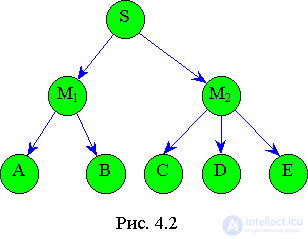
Дерево характеризуется следующими признаками:
- дерево имеет 1 элемент, на которого нет ссылок от других элементов. Этот элемент называется корнем дерева;
- в дереве можно обратиться к любому элементу путем прохождения конечного числа ссылок (указателей);
- каждый элемент дерева связан только с одним предыдущим элементом, Любой узел дерева может быть промежуточным либо терминальным (листом). На рис. 4.2 промежуточными являются элементы M1, M2, листьями - A, B, C, D, E. Характерной особенностью терминального узла является отсутствие ветвей.
Высота - это количество уровней дерева. У дерева на рис. 4.2 высота равна двум.
Количество ветвей, растущих из узла дерева, называется степенью исхода узла (на рис. 4.2 для M1 степень исхода 2, для М2 - 3). По степени исхода классифицируются деревья:
1) если максимальная степень исхода равна m, то это - m-арное дерево;
2) если степень исхода равна либо 0, либо m, то это - полное m-арное дерево;
3) если максимальная степень исхода равна 2, то это - бинарное дерево;
4) если степень исхода равна либо 0, либо 2, то это - полное бинарное дерево.
Для описание связей между узлами дерева применяют также следующую терминологию: М1 - “отец” для элементов А и В. А и В - “сыновья” узла М1.
4.1.1 Представление деревьев
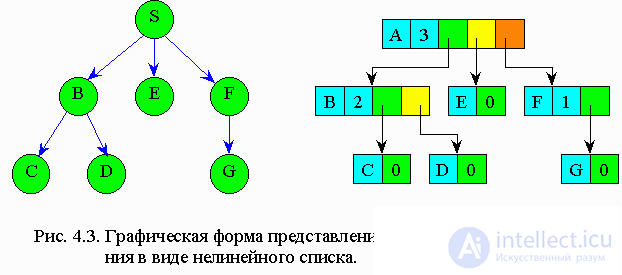
Наиболее удобно деревья представлять в памяти ЭВМ в виде связанных списков. Элемент списка должен содержать информационные поля, в которых содержится значение узла и степень исхода, а также - поля-указатели, число которых равно степени исхода (рис4.3). То есть, любой указатель элемента ориентирует данный элемент-узел с сыновьями этого узла.
4.2 Бинарные деревья
Бинарные деревья являются наиболее используемой разновидностью деревьев.
Согласно представлению деревьев в памяти ЭВМ каждый элемент будет записью, содержащей 4 поля. Значения этих полей будут соответственно ключ записи, ссылка на элемент влево-вниз, на элемент вправо-вниз и на текст записи.
При построении необходимо помнить, что левый сын имеет ключ меньший, чем у отца, а значение ключа правого сына больше значения ключа отца. Например, построим бинарное дерево из следующих элементов: 50, 46, 61, 48, 29, 55, 79. Оно имеет следующий вид:
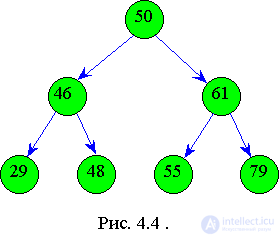
Получили упорядоченное бинарное дерево с одинаковым числом уровней в левом и правом поддеревьях. Это - идеально сбалансированное дерево, то есть дерево, в котором левое и правое поддеревья имеют уровни, отличающиеся не более чем на единицу.
Для создания бинарного дерева надо создавать в памяти элементы типа (рис. Об этом говорит сайт https://intellect.icu . 4.5):

Операция V = MakeTree(Key, Rec) - создает элемент (узел дерева) с двумя указателями и двумя полями (ключевым и информационным) .
Вид процедуры MakeTree:
Псевдокод
p = getnode
r(p) = rec
k(p) = key
v = p
left(p) = nil
right(p) = nil |
Паскаль
New(p);
p^.r := rec;
p^.k := key;
v := p;
p^.left := nil;
p^.right := nil; |
4.2.1 Сведение m-арного дерева к бинарному
Неформальный алгоритм:
1.В любом узле дерева отсекаются все ветви, кроме крайней левой, соответствующей старшим сыновьям.
2.Соединяется горизонтальными линиями все сыновья одного родителя.
3. Старшим сыном в любом узле полученной структуры будет узел, находящийся под данным узлом (если он есть).
Последовательность действий алгоритма приведена на рис. 4.6.



-
Основные операции с деревьями
1. Обход дерева.
2. Удаление поддерева.
3. Вставка поддерева.
Для выполнения
обхода дерева необходимо выполнить три процедуры:
1.Обработка корня.
2.Обработка левой ветви.
3.Обработка правой ветви.
В зависимости от того, в какой последовательности выполняются эти три процедуры, различают три вида обхода.
1.Обход сверху вниз. Процедуры выполняются в последовательности
1- 2 - 3.
2.Обход слева направо. Процедуры выполняются в последовательности
2 - 1- 3.
3.Обход снизу вверх. Процедуры выполняются в последовательности
2 - 3 -1.
В зависимости от того, какой по счету заход в узел приводит к обработке узла, получается реализация одного из трех видов обхода. Если обработка идет после первого захода в узел, то сверху вниз, если после второго, то слева направо, если после третьего, то снизу вверх (см. рис. 4. 7).
 Операция исключения поддерева.
Операция исключения поддерева. Необходимо указать узел, к которому подсоединяется исключаемое поддерево и индекс этого поддерева. Исключение поддерева состоит в том, что разрывается связь с исключаемым поддеревом, т. е. указатель элемента устанавливается в nil, а степень исхода данного узла уменьшается на единицу.
Вставка поддерева - операция, обратная исключению. Надо знать индекс включаемого поддерева, узел, к которому подвешивается дерево, установить указатель этого узла на корень поддерева, а степень исхода данного узла увеличивается на единицу. При этом в общем случае необходимо произвести перенумерацию сыновей узла, к которому подвешивается поддерево.
Алгоритм вставки и удаления рассмотрен в главе 5.
4.2.3 Алгоритм создания дерева бинарного поиска
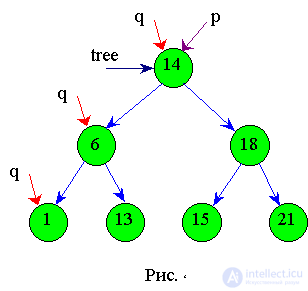
Пусть заданы элементы с ключами: 14, 18, 6, 21, 1, 13, 15. После выполнения нижеприведенного алгоритма получится дерево, изображенное на рис.4.6. Если обойти полученное дерево слева направо, то получим упорядочивание: 1, 6, 13, 14, 15, 18, 21.
Псевдокод
read (key, rec)
tree = maketree(key rec)
p = tree
q = tree
while not eof do
read (key, rec)
v = maketree(key, rec)
while p <> nil do
q = p
if key < k(p) then
p = left(p)
else
p = right(p)
endif
endwhile
if key < k(q) then
left(p) = v
else
right(p) = v
endif
if q=tree then
' только корень'
endif
return |
Паскаль
read (key, rec);
tree := maketree(key rec);
p := tree;
q := tree;
while not eof do
begin
read (key, rec);
v := maketree(key, rec);
while p <> nil do
begin
q := p;
if key < p^.k then
p := p^.left
else
p := p^.right;
end;
if key < q^.k then
p^.left := v
else
p^.right := v;
end
if q=tree
then writeln(‘Только корень’);
exit
|
4.2.4 Прохождение бинарных деревьев
В зависимости от последовательности обхода поддеревьев различают три вида обхода (прохождения) деревьев (рис.4.9):
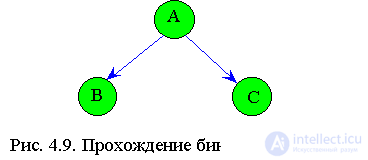
1. Сверху вниз
А, В, С.2. Слева направо или симметричное прохождение
В, А, С.3. Снизу вверх
В, С, А.Наиболее часто применяется второй способ.
Ниже приведены рекурсивные алгоритмы прохождения бинарных деревьев.
subroutine pretrave (tree) ‘сверху вниз
if tree <> nil then
print info(tree)
pretrave(left(tree))
pretrave(right(tree))
endif
return
subroutine intrave (tree) ‘симметричный
if tree <> nil then
intrave(left(tree))
print info(tree)
intrave(right(tree))
endif
return
|
Procedure pretrave (tree: tnode)
Begin
if tree <> nil then
begin
WriteLn(Tree^.Info);
Pretrave(Tree^.left);
Pretrave(Tree^.right);
End;
end;
procedure intrave (tree: tnode)
begin
if tree <> nil then
begin
intrave(Tree^.left);
writeLn(Tree^.info);
intrave(Tree^.right);
end;
end;
|
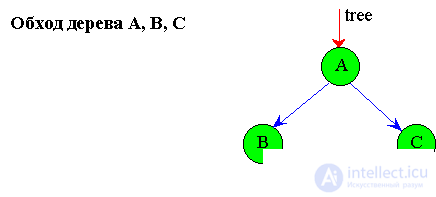
Поясним подробнее рекурсию алгоритма обхода дерева слева направо.
Пронумеруем строки алгоритма
intrave (tree):
if tree <> nil
then intrave (left(tree))
print info (tree)
intrave (right (tree))
endif
return
Обозначим указатели: t → tree; l → left; r → right
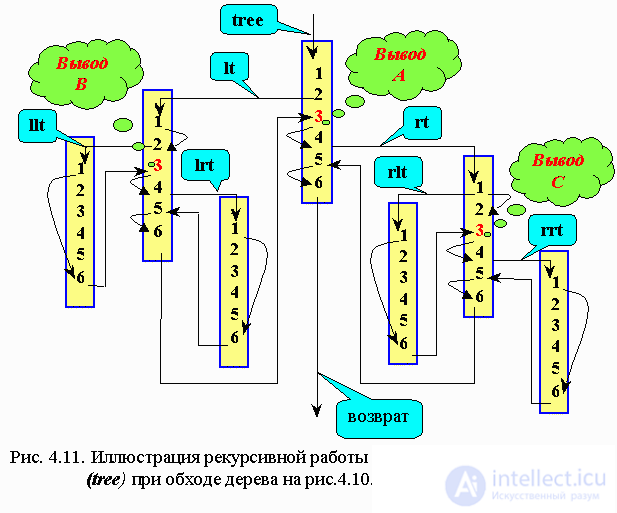
На приведенном рис. 4.11 проиллюстрирована последовательность вызова процедуры intrave (tree) по мере обхода узлов простейшего дерева, изображенного на рис. 4. 10.
На этом все! Теперь вы знаете все про рекурсивные структуры данных, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое рекурсивные структуры данных
и для чего все это нужно, а если не понял, или есть замечания,
то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Структуры данных













Комментарии
Оставить комментарий
Структуры данных
Термины: Структуры данных