Операции Тетрация и Пентация, суперкорень и применение

Лекция

Привет, Вы узнаете о том , что такое тетрация, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое тетрация, пентация, обратный суперкорень, ssrt, ssqrt , настоятельно рекомендую прочитать все из категории Алгебра.

тетрация (гипероператор-4) в математике — итерационная функция экспоненты, следующий гипероператор после возведения в степень. Тетрация используется для описания больших чисел.

Термин «тетрация», состоящий из слов «тетра-» (четыре) и «итерация» (повторение), был впервые применен английским математиком Рубеном Гудстейном в 1947 году

tetration online

Операции Тетрация и Пентация, суперкорень и применение

Определения

Тетрация как степенная башня

Для любого положительного вещественного числа a>0 или a=-1 и неотрицательного целого числа $n\geqslant 0$ , тетрацию ${}^{n}a$ можно определить рекуррентно:

${}^{0}a=1,$
${}^{n}a=a^{{({}^{{n-1}}a)}},\,n>0.$

Согласно данному определению, вычисление тетрации, записанной как «степенная башня», возведение в степень начинается с самых дальних уровней к начальному (в данной системе обозначений, с самого наивысшего показателя степени):

${}^{4}2=2^{{2^{{2^{2}}}}}=2^{{\left(2^{{\left(2^{2}\right)}}\right)}}=2^{{(2^{4})}}=2^{{16}}=65\;536.$

Или:

${}^{5}2=2^{{2^{{2^{{2^{2}}}}}}}=2^{{\left(2^{{\left(2^{{\left(2^{2}\right)}}\right)}}\right)}}=2^{{(2^{{16}})}}=2^{{65536}}.$

При этом, так как возведение в степень не является ассоциативной операцией, то вычисление выражения в другом порядке приведет к другому ответу:

$2^{{2^{{2^{2}}}}}\neq \left((2^{2})^{2}\right)^{2}=2^{{2\cdot 2\cdot 2}}=2^{8}=256.$

Или:

$2^{{2^{{2^{{2^{2}}}}}}}\neq \left(((2^{2})^{2})^{2}\right)^{2}=2^{{2\cdot 2\cdot 2\cdot 2}}=2^{{16}}=65536.$

Таким образом, степенные башни должны вычисляться сверху-вниз (или справа-налево), то есть, иначе говоря, они обладают правой ассоциативностью.

Тетрация как гипероператор

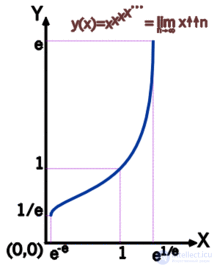
Операции Тетрация и Пентация, суперкорень и применение

$\scriptstyle {\lim \limits _{{n\to \infty }}{^{n}x}}$ . Бесконечное возведение в степень для основания $\scriptstyle {(1/e)^{e}\leqslant x\leqslant e^{{1/e}}}$ .

Тетрация является четвертой по счету гипероперацией:

сложение:
$a+b=a+\underbrace {1+1+\ldots +1}_{b};$
умножение:
$a\times b=\underbrace {a+a+\ldots +a}_{b};$
возведение в степень:
$a^{b}=\underbrace {a\times a\times \ldots \times a}_{b};$
тетрация:
${^{b}a}=\underbrace {a^{{a^{{\cdot ^{{\cdot ^{{\cdot ^{a}}}}}}}}}}_{b}.$

Здесь каждая операция является итерацией предыдущей.

Свойства

Тетрация не считается элементарной функцией (за исключением случаев с постоянным натуральным показателем, когда тетрация выражается в виде степенной башни постоянной высоты).
В силу некоммутативности тетрация имеет две обратных операции — суперлогарифм и суперкорень (аналогично тому, как возведение в степень имеет две обратные функции: арифметический корень и логарифм).

Для тетрации в общем случае неверны следующие характерные для предыдущих операторов свойства:

${}^{b}({}^{c}a)\neq {}^{c}({}^{b}a)$ , например: ${}^{3}({}^{2}2)=({}^{2}2)^{({}^{2}2)^{({}^{2}2)}}=4^{4^{4}}=4^{256}$ , но ${}^{2}({}^{3}2)=({}^{3}2)^{({}^{3}2)}=16^{16}=4^{32}$ .
${}^{b+c}a$ не равно ни ${}^{b}a+{}^{c}a$ , ни ${}^{b}a\times {}^{c}a$ , например: ${}^{1+2}3={}^{3}3=3^{27}\neq {}^{1}3+{}^{2}3\neq {}^{1}3\times {}^{2}3$ , т.к. ${}^{1}3+{}^{2}3=30;{}^{1}3\times {}^{2}3=81$ .

Примечание: однако, верно $\underbrace {\log _{a}{\log _{a}{...{\log _{a}}}}} _{b}{({}^{b+c}a)}={}^{c}a$ или $\underbrace {\log _{a}{\log _{a}{...{\log _{a}}}}} _{c}{({}^{b+c}a)}={}^{b}a$ .

Тетрация минус единицы равна минус единице:

${^{n}(-1)}=\underbrace {(-1)^{(-1)^{\cdot ^{\cdot ^{\cdot ^{(-1)}}}}}} _{n}=-1,n>0$

Терминология

Существует несколько терминов для определения понятия тетрация и за каждым из них стоит своя логика, но некоторые из них не стали общепринятыми в силу тех или иных причин. Ниже приведено несколько подобных примеров.

Термин «тетрация», использованный Рубеном Гудстейном в 1947 году в работе «Transfinite Ordinals in Recursive Number Theory» (обобщение рекуррентных представлений в теореме Гудстейна, используемых для высших операторов), имеет доминирующее положение в терминологии. Также этот термин был популяризован в работе Руди Руккера (англ. Rudy Rucker) «Infinity and the Mind».
Термин «супервозведение в степень» (англ. superexponentiation) был опубликован Бромером (англ. Bromer) в его работе «Superexponentiation» в 1987 году. Данный термин был ранее использован Эдом Нельсоном (англ. Ed Nelson) в своей книге «Предикативная Арифметика» (англ. «Predicative Arithmetic») .
Термин «гиперстепень» (англ. hyperpower) есть естественная комбинация понятий «гипер-» и «степень», который подходящим образом описывает тетрацию. Проблема лежит в понятии самого термина «гипер» относительно иерархии гипероператоров. Когда мы рассматриваем гипероператоры, термин «гипер» относится ко всем рангам, а термин «супер» относится к рангу 4, или тетрации. Таким образом, при данных обстоятельствах, понятие «гиперстепень» может ввести в заблуждение, так как оно относится только к понятию тетрация.
Термин «степенная башня» (англ. power tower) иногда используется, в форме «степенная башня порядка» для $\underbrace {a^{{a^{{\cdot ^{{\cdot ^{{\cdot ^{a}}}}}}}}}}_{n}$ .

Тетрацию также часто путают с другими тесно связанными функциями и выражениями. Ниже приведено несколько связанных терминов:

Форма	Терминология
$a^{{a^{{\cdot ^{{\cdot ^{{\cdot ^{a}}}}}}}}}$	Тетрация
$a^{{a^{{\cdot ^{{\cdot ^{{\cdot ^{{a^{x}}}}}}}}}}}$	Итерационные экспоненты
$a_{1}^{{a_{2}^{{\cdot ^{{\cdot ^{{\cdot ^{{a_{n}}}}}}}}}}}$	Вложенные экспоненты (также башни)
$a_{1}^{{a_{2}^{{a_{3}^{{\cdot ^{{\cdot ^{\cdot }}}}}}}}}$	Бесконечные экспоненты (также башни)

В первых двух выражениях {\displaystyle a} есть основание, и количество появляющихся {\displaystyle a} есть высота. Об этом говорит сайт https://intellect.icu . В третьем выражении, {\displaystyle n} есть высота, но все основания разные.

Обозначения

Системы записи, в которых тетрация может быть использована (некоторые из них позволяют использование даже более высоких итераций), включают в себя:

Имя	Форма	Описание
Стандартная форма записи	${}^{n}a$	Использована Мауером (Maurer) [1901] и Гудштейном [1947]; популяризовано в книге Руди Рюкера «Infinity and the Mind».
Стрелочная нотация Кнута	n} $a{\uparrow \uparrow }n$	Позволяет удлинение путем добавления добавочных или индексированных стрелочек, является более мощным способом.
Цепочка Конвея	$a\to n\to 2$	Позволяет удлинение путем прибавления 2 (эквивалентно вышеописанному способу), но также возможно даже более мощный способ записи, если увеличивать цепочку.
Функция Аккермана	${}^{n}2={\mathrm {A}}(4,\;n-3)+3$	Допускает особый случай {\displaystyle a=2} в записи в терминах функции Аккермана.
Итерируемая экспоненциальная форма записи	${}^{n}a=\exp _{a}^{n}(1)$	Позволяет простое удлинение до итерационных экспонент начиная со значений отличных от 1.
Обозначения Хусменд (англ. Hooshmand)	${\mathrm {uxp}}_{a}n,\quad a^{{\frac {n}{}}}$
Система записи гипероператорами	$a^{{(4)}}n,\quad {\mathrm {hyper}}_{4}(a,\;n)$	Позволяет удлинение путем прибавления 4; это дает семейство гипероператоров.
Система записи ASCII	a^^n	Так как запись стрелочка наверх используется идентично обозначению корректурного знак вставки (^), оператор тетрация может быть записан в виде (^^).
Нотация массивов Бауэрса/Берда	{a, b,2}	{a, b,c} = a^^^…^^^b (c стрелок сверхстепени).

Одна из вышеприведенных систем использует систему записи итерированных экспонент; в общем случае это определяется следующим образом:

$\exp _{a}^{n}(x)=\underbrace {a^{{a^{{\cdot ^{{\cdot ^{{\cdot ^{{a^{x}}}}}}}}}}}}_{n}.$

Не так много обозначений существует для итерированных экспонент, но несколько из них показаны ниже:

Имя	Форма	Описание
Стандартная форма записи	$\exp _{a}^{n}(x)$	Система записи $\exp _{a}(x)=a^{x}$ и итерационная система записи $f^{n}(x)$ была введена Эйлером.
Стрелочная нотация Кнута	$(a{\uparrow })^{n}(x)$	Позволяет для суперстепеней и суперэкспоненциальных функций увеличивать число стрелочек.
Гипер-Е нотация	E(a)x#n
Система записи Иоанна Галидакиса (англ. Ioannis Galidakis)	${}^{n}(a,\;x)$	Допускает использование больших выражений в основании.
ASCII (добавочный)	a^^n@x	Основана на взгляде, что итерационная экспонента есть добавочная тетрация.
ASCII (стандартный)	exp_a^n(x)	Основана на стандартной форме записи.

Примеры

В нижеприведенной таблице большинство значений слишком огромны, чтобы их записать в экспоненциальном представлении, по этой причине используется система записи в виде итерационных экспонент, чтобы представить их с основанием 10. Значения, содержащие десятичную запятую, являются приблизительными. Например, четвертая тетрация от 3 (т.е. $3^{3^{3^{3}}}$ ) начинается цифрами 1258, заканчивается цифрами 39387 и имеет 3638334640025 цифр, последовательность A241292 в OEIS.

	${}^{2}x$	${}^{3}x$	${}^{4}x$
1	1	1	1
2	4	16	65 536
3	27	7 625 597 484 987	$\exp _{{10}}^{3}(1{,}09902)$
4	256	$\exp _{{10}}^{2}(2{,}18788)$	$\exp _{{10}}^{3}(2{,}18726)$
5	3 125	$\exp _{{10}}^{2}(3{,}33931)$	$\exp _{{10}}^{3}(3{,}33928)$
6	46 656	$\exp _{{10}}^{2}(4{,}55997)$	$\exp _{{10}}^{3}(4{,}55997)$
7	823 543	$\exp _{{10}}^{2}(5{,}84259)$	$\exp _{{10}}^{3}(5{,}84259)$
8	16 777 216	$\exp _{{10}}^{2}(7{,}18045)$	$\exp _{{10}}^{3}(7{,}18045)$
9	387 420 489	$\exp _{{10}}^{2}(8{,}56784)$	$\exp _{{10}}^{3}(8{,}56784)$
10	10 000 000 000	$\exp _{{10}}^{3}(1)$	$\exp _{{10}}^{4}(1)$

Тетрация мнимой единицы или комплексных числел.

Это сложный и до сих пор открытый вопрос в математике.

Тетрация для мнимой единицы i — или, более обще, тетрация для нецелых степеней и комплексных чисел —

не имеет общепринятого простого ответа в том же смысле, что и i²= −1.

Тетрация (суперстепень, гипероператор-4) — это итерационное возведение в степень.

Обозначается как na и определяется рекурсивно:

a^^n = a ^a (n раз)

Например:

i^^1 = i
i^^2 = i ⁱ
i^^3 = i ⁽ⁱⁱ⁾
i^^4 = i^(i(ii))

Вычисление первых тетраций ni

Чтобы найти конкретные значения тетрации для i, нужно вычислять степени i с комплексным показателем:

i^^2 = iⁱ

Для вычисления iⁱиспользуем формулу для комплексной степени b^^a = e^blna.

Найдем натуральный логарифм ln(i):

i = e^iπ/2

ln i = i π/2

(Основное значение)
Подставим в формулу iⁱ:

i^^2 = iⁱ = e^i⋅lni = e^i⋅(iπ/2) = e^i2π/2 = e^−π/2 ≈ 0.207879576...

Открытые проблемы

Неизвестно, являются ли nπ или ne целыми числами при каком-либо натуральном n. Неизвестно даже, является ли ${^4\pi}=\pi^{\pi^{\pi^\pi}}$ целым.
Неизвестно, может ли ${^n q}$ быть рациональным числом, если — целое число, большее 3, а — рациональное, но не целое число (для $n=2,\,3$ ответ отрицателен) .
Ни для какого целого неизвестно, является ли положительный корень уравнения ${^{n}x}=2$ рациональным, алгебраическим иррациональным или трансцендентным числом.

Операция, обратной тетрации

Квадратный суперкорень заданного числа, переменной(ых) или математического выражения обозначается как ssrt(x), ssqrt(x) или√𝑥𝑠) — редкая математическая функция, является обратной к тетрации.

Функция ssrt(x) представляет собой операцию, обратную тетрации (повторному возведению в степень), и ее вычисление использует функцию Ламберта W или итерационный подход метода Ньютона-Рафсона . Калькулятор использует первый метод и поддерживает выражения с несколькими переменными.

пентация

Пентация — это повторяющаяся тетрация, как тетрация — повторяющееся возведение в степень. Она является гипероператором, это некоммутативная функция и, отсюда, имеет две обратные функции, которые можно назвать пента-корень и пента-логарифм (аналогично тому, как возведение в степень имеет две обратные функции: арифметический корень и логарифм).

Избранные значения

$2\uparrow ^{{3}}2={^{{2}}2}=4$
$2\uparrow ^{3}3={^{^{2}2}2}={^{4}2}=65536$
$2\uparrow ^{3}4={^{^{^{2}2}2}2}={^{65536}2}=2^{2^{2^{\cdot ^{\cdot ^{\cdot ^{2}}}}}}{\mbox{ (степенная башня высотой 65536) }}\approx \exp _{10}^{65533}(4{,}29508)$
$3\uparrow ^{3}2={^{3}3}=3^{3^{3}}=3^{27}=7625597484987$
$3\uparrow ^{3}3={^{^{3}3}3}={^{7625597484987}3}=3^{3^{3^{\cdot ^{\cdot ^{\cdot ^{3}}}}}}{\mbox{ (степенная башня высотой 7625597484987) }}\approx \exp _{10}^{7625597484986}(1{,}09902)$
$4\uparrow ^{3}2={^{4}4}=4^{4^{4^{4}}}=4^{4^{256}}\approx \exp _{10}^{3}(2{,}19)$ (число с более чем 10153 цифр)
$5\uparrow ^{3}2={^{5}5}=5^{5^{5^{5^{5}}}}=5^{5^{5^{3125}}}\approx \exp _{10}^{4}(3{,}33928)$ (число с более чем 10102184 цифр)

Применение практическое Тетрации и пентации

Тетрация и пентация являются операциями в высшей арифметике, которые используются в математике для возведения в очень большие итеративные степени. Однако, их практическое применение в различных отраслях ограничено. Вот несколько возможных областей, в которых можно найти применение для этих операций:

1. Криптография: Тетрация и пентация могут использоваться в криптографии для создания сложных алгоритмов шифрования. Они могут обеспечить сильную защиту данных при математическом моделировании сложных преобразований.

2. Анализ данных: В некоторых случаях тетрация и пентация могут быть использованы для взвешивания данных с разной степенью значимости. Это может быть полезным при разработке алгоритмов машинного обучения или анализе больших объемов данных.

3. Моделирование сложных процессов: Тетрация и пентация могут быть применены в научной работе и исследованиях для моделирования сложных процессов или систем. Это может помочь ученым понять и предсказать поведение таких систем, где нелинейные итеративные процессы играют роль.

4. Компьютерная графика: Вычисления с использованием тетрации и пентации могут быть востребованы в компьютерной графике для реалистического моделирования эффектов рефлексии или освещения. Они позволяют создавать более сложные и реалистичные визуальные эффекты. Однако в большинстве отраслей, таких как бизнес, финансы или инженерия, применение тетрации и пентации ограничено из-за их сложности и малой практической пользы. В основном, эти операции используются в научных и академических исследованиях для изучения абстрактных математических концепций.

Вау!! 😲 Ты еще не читал? Это зря!

гексация ,
гипероператор ,
Функция Аккермана
Функция Веблена
Пси-функции Бухгольца
Гипероператор
Быстрорастущая иерархия
Медленнорастущая иерархия
Иерархия Харди
суперкорень

Исследование, описанное в статье про тетрация, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое тетрация, пентация, обратный суперкорень, ssrt, ssqrt и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгебра

Операции Тетрация и Пентация, суперкорень и применение

Определения

Тетрация как степенная башня

Тетрация как гипероператор

Свойства

Терминология

Обозначения

Примеры

Тетрация мнимой единицы или комплексных числел.

Открытые проблемы

Операция, обратной тетрации

пентация

Избранные значения

Применение практическое Тетрации и пентации

Вау!! 😲 Ты еще не читал? Это зря!

Комментарии

Оставить комментарий

Алгебра

Термины: Алгебра