Лекция
Game: Perform tasks and rest cool.3 people play!
Play gameПривет, Вы узнаете о том , что такое кинематика, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое кинематика, вращение абсолютно твердого тела, движение тела брошенного под углом к горизонту, ускорение тела , настоятельно рекомендую прочитать все из категории Физические основы механики.
Механика изучает закономерности наиболее простой формы движения тел — перемещение в пространстве и причины, вызывающие эти движения.
Типичная задача механики: зная состояние системы (координаты и скорости) в некоторый начальный момент времени 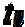 , а также законы, управляющие движением, определить состояние системы во все последующие моменты времени
, а также законы, управляющие движением, определить состояние системы во все последующие моменты времени 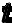 . Для этого используются уравнения движения — уравнения, позволяющие определить положение материальной точки (системы) в пространстве в любой момент времени по известным начальным условиям. Опыт показывает, что знания начальных скоростей и координат системы достаточно для прослеживания ее дальнейшей судьбы. С математической точки зрения это означает, что уравнения движения не содержат более высоких производных по времени, нежели вторая (как говорят, это уравнения второго порядка).
. Для этого используются уравнения движения — уравнения, позволяющие определить положение материальной точки (системы) в пространстве в любой момент времени по известным начальным условиям. Опыт показывает, что знания начальных скоростей и координат системы достаточно для прослеживания ее дальнейшей судьбы. С математической точки зрения это означает, что уравнения движения не содержат более высоких производных по времени, нежели вторая (как говорят, это уравнения второго порядка).
Почему это так — вопрос запрещенный. Каковы эти уравнения — мы увидим в дальнейшем.
кинематика изучает движение тел, не вдаваясь в причины, его вызывающие.
Кинематика оперирует с такими величинами, как перемещение, путь, скорость, ускорение.
Ни одна физическая задача не может быть решена абсолютно точно. Решая задачу приближенно, пренебрегают некоторыми факторами, которые в данном случае не существенны, то есть абстрагируются от них. Одна из абстракций в механике — материальная точка.
Материальная точка — это тело, размеры, форма и внутренняя структура которого в данной задаче несущественны.
Механическая система — совокупность тел, выделенная для рассмотрения. Если линейные размеры тел малы по сравнению с расстояниями между ними, а вращением тел вокруг осей, проходящих через них, можно пренебречь, то такую систему можно считать состоящей из материальных точек. Например, вычисляя время автомобиля в пути, можно пренебречь его линейными размерами по сравнению с проходимым расстоянием, то есть рассматривать его как материальную точку. Но, изучая вращение колеса автомобиля, мы должны учесть его форму, массу, размеры. В этом случае первый уровень абстракции нас уже не удовлетворит, и мы переходим на следующий уровень.
Game: Perform tasks and rest cool.3 people play!
Play gameАбсолютно твердое тело — это тело, деформациями которого можно в условиях данной задачи пренебречь.
Здесь мы не пренебрегаем размерами тела, но считаем неизменными расстояния между двумя его любыми точками. На этом уровне можно решать задачи о вращении колес и блоков, о работе гироскопов и т. п. Иначе говоря, те задачи, где деформации тела малы по сравнению с его линейными размерами.
Но если нас интересует именно деформация тел, скажем, при расчетах мостов, поведении балок и арок, то мы из области классической механики попадаем в сферу действия других научных дисциплин — теоретической механики, теории упругости и т. п. В этом курсе мы ограничимся первыми двумя уровнями абстракции.
Game: Perform tasks and rest cool.3 people play!
Play gameЧисло степеней свободы механической системы — это число независимых скалярных величин, задание значений которых необходимо для однозначного определения конфигурации системы
Так как наше пространство трехмерно, число степеней свободы материальной точки равно трем. Для системы из 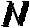 материальных точек, между которыми нет жестких связей, число степеней свободы равно, естественно,
материальных точек, между которыми нет жестких связей, число степеней свободы равно, естественно, 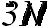 . При наличии жестких связей между точками число степеней свободы уменьшается на число таких связей. Так, для однозначного указания положения абсолютно твердого тела в пространстве нам надо задать:
. При наличии жестких связей между точками число степеней свободы уменьшается на число таких связей. Так, для однозначного указания положения абсолютно твердого тела в пространстве нам надо задать:
Отметим, что упомянутые выше точки тела не должны обязательно находиться на поверхности абсолютно твердого тела или внутри его, они должны быть жестко связаны с телом, то есть расстояние от выбранной точки до любой точки тела не должно меняться в процессе движения.
Таким образом, число степеней свободы для абсолютно твердого тела равняется шести. Для каждой степени свободы системы должно быть написано свое уравнение движения, то есть количество скалярных уравнений движения системы должно совпадать с числом ее степеней свободы.
Тот факт, что у абсолютно твердого тела именно шесть степеней свободы можно пояснить еще и таким способом. Достаточно очевидно, что указание положения трех жестко связанных с телом и не лежащих на одной прямой точек, однозначно определяет положение всего тела в пространстве. Такие три точки определяют некий треугольник. У трех точек 9 степеней свободы, но это точки абсолютно твердого тела, следовательно, расстояния между ними — длины сторон треугольника — неизменны. Это три связи, следовательно, независимыми из девяти величин остаются только шесть: у абсолютно твердого тела шесть степеней свободы.
Задание трех координат некоторой жестко связанной с телом точки и трех углов, определяющих ориентацию тела удобно тем, что подсказывает разделение всех шести степеней свободы тела на два вида: три «поступательных» и три «вращательных» степени свободы. Мы вернемся к этому вопросу при рассмотрении вращательного движения протяженных тел.
Непрерывная линия, которую описывает точка при своем движении, называется траекторией.
Понятие траектории является существенно классическим и теряет привычный смысл в квантовой механике. В зависимости от формы траектории различают прямолинейное движение, движение по окружности и другие виды криволинейного движения.
Game: Perform tasks and rest cool.3 people play!
Play game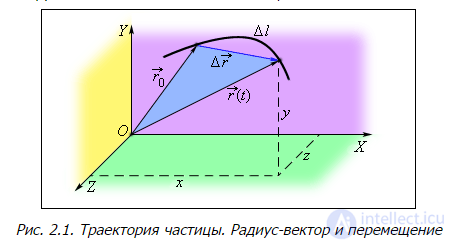
Рис. 2.1. Траектория частицы. Радиус-вектор и перемещение
Положение материальной точки 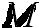 в пространстве задается радиус-вектором
в пространстве задается радиус-вектором 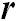 (см. п. 1.4). Поскольку мы рассматриваем движение точки, радиус-вектор зависит от времени:
(см. п. 1.4). Поскольку мы рассматриваем движение точки, радиус-вектор зависит от времени:
Game: Perform tasks and rest cool.3 people play!
Play game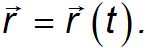
Если в какой-то момент времени t1 положение материальной точки в пространстве было r = r(t1), а в момент времени t2 стало r = r(t2), то говорят о перемещении материальной точки из точки 1 в точку 2 (рис. 2.2.).
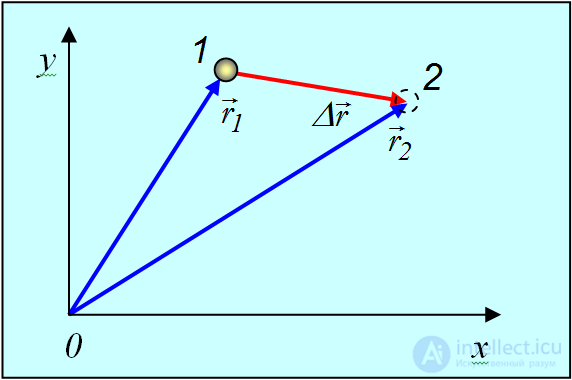
Рис. 2.2. Криволинейное движение частицы
Перемещение частицы за время от t1 до t2 — это вектор 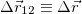 , проведенный из положения частицы в момент времени t1 в ее положение в момент t2.
, проведенный из положения частицы в момент времени t1 в ее положение в момент t2.
Из рис. 2.2. очевидно, что
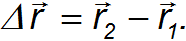
Перемещение есть вектор характеризуется модулем 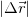 и направлением, причем перемещения, как и положено векторам, складываются по правилу параллелограмма.
и направлением, причем перемещения, как и положено векторам, складываются по правилу параллелограмма.
Важно отметить, что
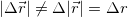
От перемещения следует отличать пройденный материальной точкой путь.
Путь за время от t1 до t2 — скалярная величина, равная длине участка траектории, пройденного материальной точкой за рассматриваемый промежуток времени.
Путь — неотрицательная, неубывающая функция времени. Может случиться так, что перемещение равно нулю, а путь достигает значительной величины. Например, вы утром выезжаете из гаража, ездите целый день по городу и к вечеру ставите машину на прежнее место. Поскольку начальное и конечное положения совпали (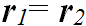 ), то перемещение равно нулю:
), то перемещение равно нулю:
Game: Perform tasks and rest cool.3 people play!
Play game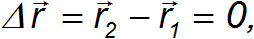
а пройденный путь отмечен на счетчике.
Чтобы вычислить пройденный путь, надо траекторию разбить на малые участки (рис. 2.3.).
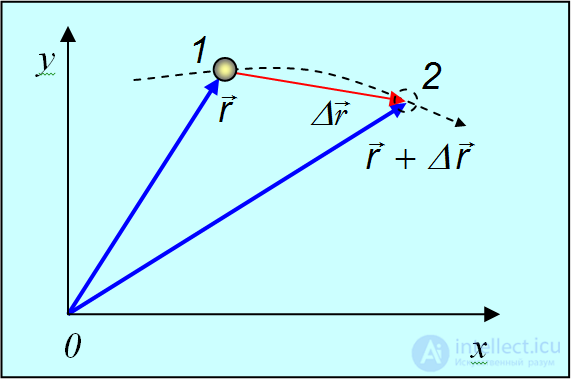
Рис. 2.3. Путь и перемещение при бесконечно малом перемещении
Game: Perform tasks and rest cool.3 people play!
Play game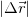 будет приблизительно равна пройденному пути
будет приблизительно равна пройденному пути  , причем совпадение будет тем точнее, чем мельче наше разбиение. При разбиении на бесконечно малые участки
, причем совпадение будет тем точнее, чем мельче наше разбиение. При разбиении на бесконечно малые участки 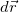 имеем равенство
имеем равенство
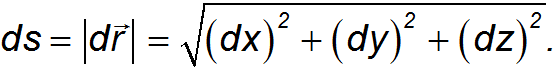
Для нахождения полного пути 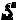 надо просуммировать все эти бесконечно малые пути, то есть вычислить интеграл
надо просуммировать все эти бесконечно малые пути, то есть вычислить интеграл
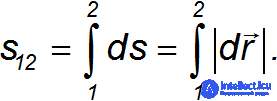
Здесь интегрирование ведется вдоль траектории от начальной точки 1 до конечной точки 2.
Интерактивная модель (рис. 2.4.) иллюстрирует разницу между путем и перемещением.
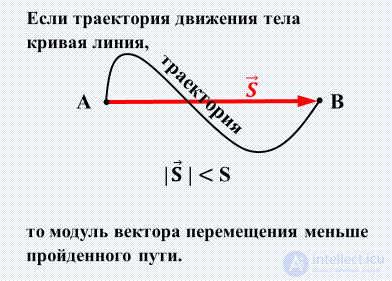
Рис. 2.4. Путь и перемещение
Скорость — векторная величина, характеризующая не только быстроту передвижения частицы по траектории, но и направление, в котором движется частица в каждый момент времени.
Средняя скорость за время от t1 до t2 равна отношению перемещения 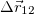 за это время к промежутку времени
за это время к промежутку времени 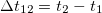 , за которое это перемещение имело место:
, за которое это перемещение имело место:
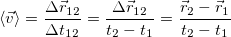
Тот факт, что это именно средняя скорость мы будем отмечать, заключая среднюю величину в угловые скобки: <...> , как это сделано выше.
Приведенная выше формула для среднего вектора скорости есть прямое следствие общего математического определения среднего значения <f(x)> произвольной функции f(x) на промежутке [a,b]:
Game: Perform tasks and rest cool.3 people play!
Play game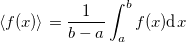
Действительно
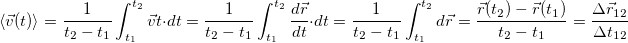
Средняя скорость может оказаться слишком грубой характеристикой движения. Например, средняя скорость за период колебаний всегда равна нулю, в независимости от характера этих колебаний, по той простой причине, что за период — по определению периода — колеблющееся тело вернется в исходную точку и, следовательно, перемещение за период всегда равно нулю. По этой и ряду других причин, вводится мгновенная скорость — скорость в данный момент времени. В дальнейшем, подразумевая мгновенную скорость, будем писать просто: «скорость», опуская слова «мгновенная» или «в данный момент времени» всегда, когда это не может привести к недоразумениям.Для получения скорости в момент времени t надо сделать очевидную вещь: вычислить предел отношения 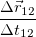 при стремлении промежутка времени t2 – t1 к нулю. Сделаем переобозначения: t1 = t и t2 = t +
при стремлении промежутка времени t2 – t1 к нулю. Сделаем переобозначения: t1 = t и t2 = t + 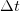 и перепишем верхнее соотношение в виде:
и перепишем верхнее соотношение в виде:
Game: Perform tasks and rest cool.3 people play!
Play gameСкорость в момент времени t равна пределу отношения перемещения 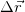 за время
за время 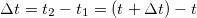 к промежутку времени, за которое это перемещение имело место, при стремлении последнего к нулю
к промежутку времени, за которое это перемещение имело место, при стремлении последнего к нулю
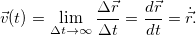
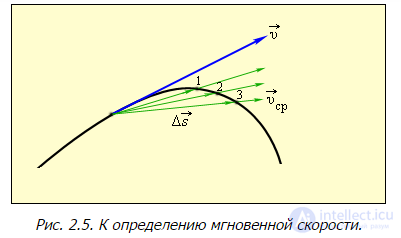
Рис. 2.5. К определению мгновенной скорости.
В данный момент мы не рассматриваем вопрос о существовании этого предела, предполагая, что он существует. Отметим, что если 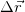 и
и 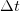 есть конечное перемещение и конечный промежуток времени, то
есть конечное перемещение и конечный промежуток времени, то 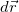 и
и 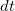 — их предельные величины: бесконечно малое перемещение и бесконечно малый промежуток времени. Так что правая часть определения скорости
— их предельные величины: бесконечно малое перемещение и бесконечно малый промежуток времени. Так что правая часть определения скорости
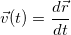
есть ничто иное как дробь — частное от деления 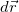 на
на 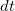 , поэтому последнее соотношение может быть переписано и весьма часто используется в виде
, поэтому последнее соотношение может быть переписано и весьма часто используется в виде
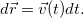
Здесь и далее мы часто для удобства будем использовать восходящее к Ньютону обозначение производной по времени в виде точки над соответствующей величиной:
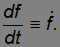
По геометрическому смыслу производной, вектор скорости в каждой точке траектории направлен по касательной к траектории в этой точке в ее сторону движения.
Видео 2.1. Вектор скорости направлен по касательной к траектории. Эксперимент с точилом.
Любой вектор можно разложить по базису (для единичных векторов базиса, другими словами, единичных векторов, определяющих положительные направления осей OX,OY,OZ используем обозначения 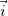 ,
, 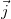 ,
, 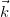 или
или 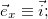
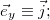
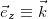 , соответственно). Коэффициентами такого разложении являются проекции вектора на соответствующие оси. Важно следующее: в алгебре векторов доказано, что разложение по базису единственно. Разложим по базису радиус-вектор некоторой движущейся материальной точки
, соответственно). Коэффициентами такого разложении являются проекции вектора на соответствующие оси. Важно следующее: в алгебре векторов доказано, что разложение по базису единственно. Разложим по базису радиус-вектор некоторой движущейся материальной точки
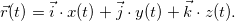
Учитывая постоянство декартовых единичных векторов 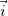 ,
, 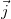 ,
, 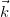 , продифференцируем это выражение по времени
, продифференцируем это выражение по времени
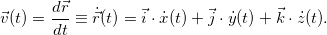
С другой стороны, разложение по базису вектора скорости имеет вид
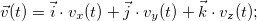
Game: Perform tasks and rest cool.3 people play!
Play game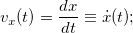
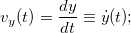
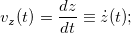
Модуль вектора скорости равен
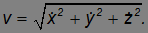
Получим еще одно, важное, выражение для модуля вектора скорости.
Уже отмечалось, что при 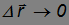 величина |
величина |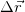 | все меньше и меньше отличается от соответствующего пути
| все меньше и меньше отличается от соответствующего пути 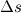 (см. рис. 2). Поэтому
(см. рис. 2). Поэтому
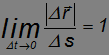
и в пределе (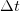 >0)
>0)
Game: Perform tasks and rest cool.3 people play!
Play game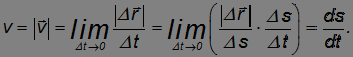
Иными словами, модуль скорости — это производная пройденного пути по времени.
Окончательно имеем:
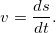
Средний модуль вектора скорости, определяется следующим образом:
Среднее значение модуля вектора скорости равно отношению пройденного пути ко времени, в течение которого этот путь был пройден:
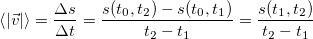
Здесь s(t1, t2) — путь за время от t1 до t2 и, соответственно, s(t0, t2) — путь за время от t0 до t2 и s(t0, t2) — путь за время от t0 до t1.
Средний вектор скорости или просто средняя скорость, как указано выше, равен
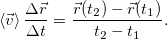
Отметим, что прежде всего, это вектор, его модуль — модуль среднего вектора скорости не следует путать со средним значением модуля вектора скорости. В общем случае они не равны: модуль среднего вектора вовсе не равен среднему модулю этого вектора 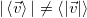 . Две операции: вычисление модуля и вычисление среднего, в общем случае, переставлять местами нельзя.
. Две операции: вычисление модуля и вычисление среднего, в общем случае, переставлять местами нельзя.
Рассмотрим пример. Пусть точка движется в одну сторону. На рис. 2.6. показан график пройденного ею пути s в от времени 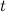 (за время от 0 до t). Используя физический смысл скорости, найти с помощью этого графика момент времени
(за время от 0 до t). Используя физический смысл скорости, найти с помощью этого графика момент времени 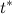 , в который мгновенная скорость равна средней путевой скорости за первые
, в который мгновенная скорость равна средней путевой скорости за первые 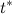 секунд движения точки.
секунд движения точки.
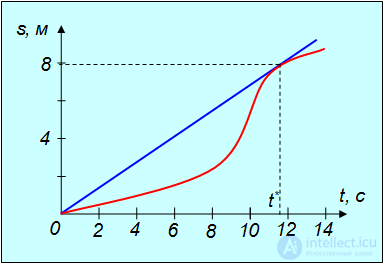
Рис. 2.6. Определение мгновенной и средней скорости тела
Модуль скорости в данный момент времени 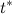
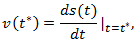
Game: Perform tasks and rest cool.3 people play!
Play game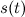 точке соответствующей моменту времени t*. Средний модуль скорости
точке соответствующей моменту времени t*. Средний модуль скорости 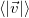 за промежуток времени от 0 до t* есть угловой коэффициент секущей, проходящей через точки того же графика, соответствующие началу t = 0 и концу t = t* временного интервала. Нам надо найти такой момент времени t*, когда оба угловых коэффициента совпадают. Для этого через начало координат проводим прямую, касательную к траектории. Как видно из рисунка точка касания этой прямой графика s(t) и дает t*. В нашем примере получается
за промежуток времени от 0 до t* есть угловой коэффициент секущей, проходящей через точки того же графика, соответствующие началу t = 0 и концу t = t* временного интервала. Нам надо найти такой момент времени t*, когда оба угловых коэффициента совпадают. Для этого через начало координат проводим прямую, касательную к траектории. Как видно из рисунка точка касания этой прямой графика s(t) и дает t*. В нашем примере получается 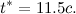
Если путь  , пройденный материальной точкой за промежуток времени от t1 до t2, разбить на достаточно малые участки
, пройденный материальной точкой за промежуток времени от t1 до t2, разбить на достаточно малые участки 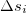 , то для каждого
, то для каждого 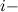 го участка выполняется условие
го участка выполняется условие
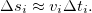
Тогда весь путь приближенно равен сумме
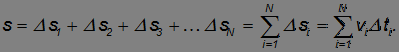
При стремлении всех 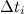 к нулю это приближенное равенство становится точным, то есть
к нулю это приближенное равенство становится точным, то есть
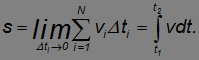
Game: Perform tasks and rest cool.3 people play!
Play game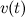 , осью времени и вертикальными прямыми, проходящими через точки с абсциссами
, осью времени и вертикальными прямыми, проходящими через точки с абсциссами 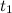 и
и 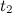 (рис. 2.7.).
(рис. 2.7.).
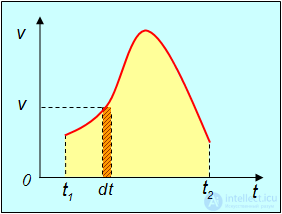
Рис. 2.7. Определение пройденного пути по графику зависимости скорости от времени
При равномерном движении величина скорости  постоянна и может быть вынесена из-под знака интеграла:
постоянна и может быть вынесена из-под знака интеграла:
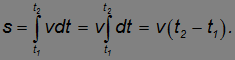
Так как модуль скорости 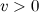 , то пройденный телом путь с течением времени может только возрастать (или быть постоянным, когда тело покоится).
, то пройденный телом путь с течением времени может только возрастать (или быть постоянным, когда тело покоится).
Если нас интересует перемещение материальной точки за то же время, то мы так же разбиваем траекторию на малые участки, но суммируем теперь векторы перемещения:
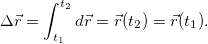
Учитывая связь перемещения с вектором скорости
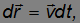
получаем
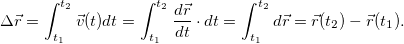
В отличие от выражения для пройденного пути под интегралом здесь стоит не модуль, а вектор скорости. Точно так же при равномерном прямолинейном движении, когда 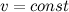 , мы можем вынести скорость из-под знака интеграла:
, мы можем вынести скорость из-под знака интеграла:
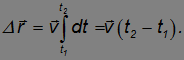
Чтобы практически найти перемещение, интеграл, представленный в векторной форме, необходимо записать в виде интегралов для проекций
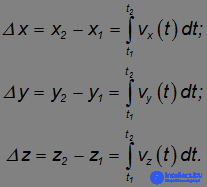
Здесь x1, y1, z1 — координаты точки в момент времени t1, а x2, y2, z2 — координаты точки в момент времени t2, соответственно величина перемещения при этом равна
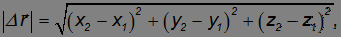
а направление вектора перемещения определяется соотношением:
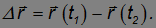
Game: Perform tasks and rest cool.3 people play!
Play game в
в  , был выбран оптимальный маршрут, показанный на рис. 2.8. Найти соотношение между синусами углов α и β.
, был выбран оптимальный маршрут, показанный на рис. 2.8. Найти соотношение между синусами углов α и β.
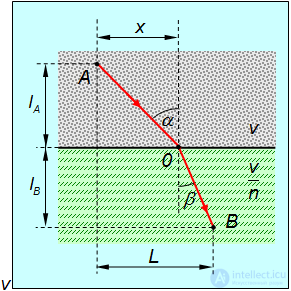
Рис. 2.8. Оптимальный маршрут из пункта А в пункт В
Все расстояния указаны на рисунке. Время 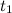 , затрачиваемое на путь
, затрачиваемое на путь 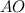 , преодолеваемый со скоростью
, преодолеваемый со скоростью  , равно
, равно
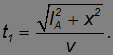
Время t2, затрачиваемое на путь 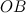 , преодолеваемый со скоростью
, преодолеваемый со скоростью 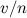 , равно
, равно
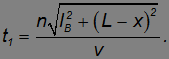
Полное время в пути, будет
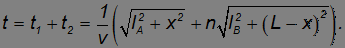
Game: Perform tasks and rest cool.3 people play!
Play game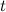 по координате
по координате  точки перехода с бетона на траву:
точки перехода с бетона на траву:
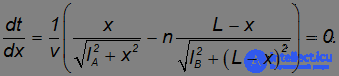
Поскольку
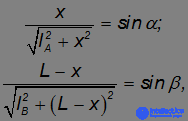
находим, что

то есть
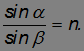
Сходство с известным законом преломления света на границе двух сред не случайно: природа устроена так, что свет выбирает путь, требующий минимального времени. Это так называемый принцип Ферма, который мы подробно рассмотрим в соответствующем разделе.
Скорость частицы 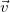 может изменяться со временем, как по величине, так и по направлению.
может изменяться со временем, как по величине, так и по направлению.
Быстрота изменения вектора скорости называется ускорением.
Быстрота (скорость) изменения во времени любой величины определяется производной по времени от этой величины. Это общее правило касается и вектора скорости.
Ускорение 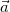 равно производной вектора
равно производной вектора 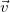 по времени t, или, что то же самое — второй производной по времени радиус-вектора
по времени t, или, что то же самое — второй производной по времени радиус-вектора 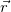 :
:
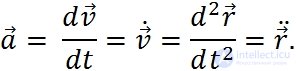
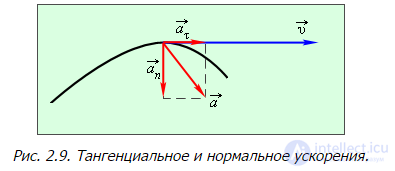
Рис. 2.9. Тангенциальное и нормальное ускорения.
Если известны зависимость от времени ускорения а = a(t) и начальная скорость v0 (при t = t0), то значение скорости в любой момент времени t равно
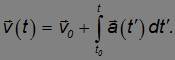
Game: Perform tasks and rest cool.3 people play!
Play game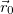 тела в начальный момент t = t0 , то мы можем найти не только скорость, но и положение тела в любой момент времени:
тела в начальный момент t = t0 , то мы можем найти не только скорость, но и положение тела в любой момент времени:
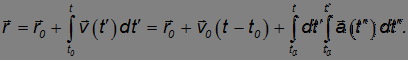
При равноускоренном движении ( 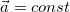 ) интегралы легко вычисляются и мы получаем:
) интегралы легко вычисляются и мы получаем:
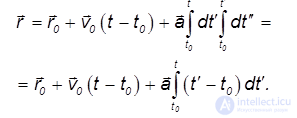
Вычисление последнего интеграла приводит к закону равноускоренного движения материальной точки
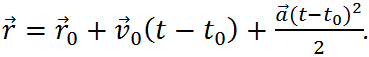
При прямолинейном движении векторы перемещения, скорости и ускорения направлены вдоль одной и той же прямой, совпадающей с траекторией. Поэтому направление прямой можно принять за ось x и оперировать с ускорением и скоростью как с проекциями векторов на эту ось, то есть как с алгебраическими величинами. При этом индекс, обозначающий проекцию вектора на ось, опускают.
Видео 2.2. Скатывание тележки с наклонной плоскости как пример равноускоренного движения.
Game: Perform tasks and rest cool.3 people play!
Play gameПредставим себе материальную точку, движущуюся по некоторой криволинейной траектории 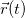 . Запишем скорость в виде
. Запишем скорость в виде
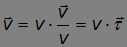
и заметим, что вектор
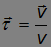
— это единичный вектор, касательный к траектории и совпадающий по направлению с вектором скорости. Продифференцируем вектор скорости, записанный в данном представлении, и получим
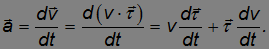
Мы представили ускорение в виде двух слагаемых. Заметим прежде всего, что слагаемые ортогональны друг другу. Действительно, поскольку вектор 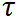 — единичный, то
— единичный, то
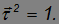
Дифференцируя это скалярное произведение, получаем
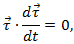
то есть
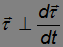
по свойству скалярного произведения.
Таким образом, мы разложили ускорение на сумму двух взаимно ортогональных составляющих, обозначем их 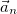 и
и 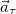 :
:
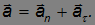
Обсудим физический смысл каждого слагаемого. Слагаемое
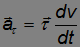
— это тангенциальное ускорение, которое характеризует быстроту изменения модуля скорости. Эта часть полного ускорения 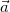 направлена либо по скорости, когда производная dv/dt > 0, то есть движение ускоренное, либо в сторону противоположную скорости, когда эта производная dv/dt < 0, то есть движение замедленное. Если движение равномерное dv/dt = 0, то есть скорость, если и меняется, то лишь по направлению, то тангенциальная часть ускорения равна нулю:
направлена либо по скорости, когда производная dv/dt > 0, то есть движение ускоренное, либо в сторону противоположную скорости, когда эта производная dv/dt < 0, то есть движение замедленное. Если движение равномерное dv/dt = 0, то есть скорость, если и меняется, то лишь по направлению, то тангенциальная часть ускорения равна нулю:
Game: Perform tasks and rest cool.3 people play!
Play game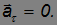
Слагаемое
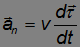
направлено по нормали к траектории — перпендикулярно касательной к траектории и называется нормальным ускорением. Если тангенциальное ускорение определяет скорость, с которой меняется модуль вектора скорости, то нормальное ускорение определяет скорость, с которой меняется направление вектора скорости.
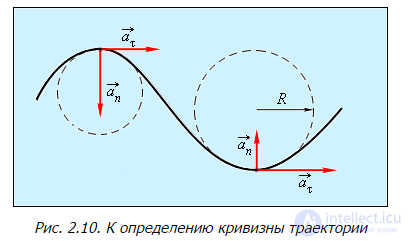
Рис. 2.10. К определению кривизны траектории
Game: Perform tasks and rest cool.3 people play!
Play game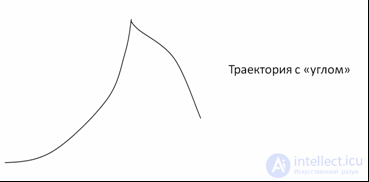
Рис. 2.11.
Такую «гладкую» кривую на любом ее бесконечно малом участке можно заменить (рис. 2.12) участком окружности некоторого радиуса. Радиус этой окружности, аппроксимирующей траекторию на ее бесконечно малом участке в окрестности некоторой точки, принято называть радиусом кривизны траектории в этой точке. Центр этой окружности принято называть центром кривизны траектории в данной точке. Кривизной траектории называется величина C = 1/R. Подчеркнем, что радиус кривизны, как и центр кривизны траектории — ее локальные характеристика: каждой точке траектории соответствует свой радиус кривизны и свой центр кривизны. Исключениями являются: 1) окружность, ее радиус кривизны во всех ее точках один и тот же и равен радиусу окружности, центр кривизны «один на всех» и совпадает с центром окружности, и 2) прямая, для любой точки прямой радиус кривизны бесконечен, а центр кривизны находится в бесконечно удаленной от прямой точке. Это легко понять: давайте увеличивать радиус окружности, чем больше радиус окружности, тем ближе любой ее конечный участок к участку прямой. На равнине, лучше всего на пляже, с высоты человеческого роста до горизонта не более пяти километров, — в этих пределах Земля плоская.
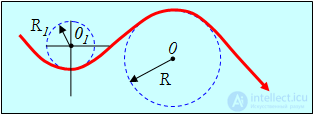
Рис. 2.12. К определению радиуса кривизны траектории
Вычислим модуль производной 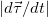 , входящей в выражение для нормального ускорения. Направлен вектор
, входящей в выражение для нормального ускорения. Направлен вектор 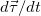 по нормали к траектории к центру к центру кривизны, что поясняет рис. 2.13.
по нормали к траектории к центру к центру кривизны, что поясняет рис. 2.13.
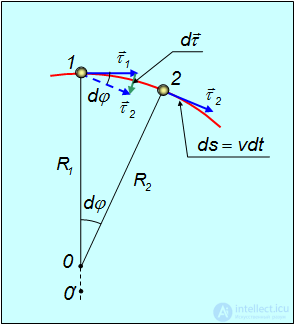
Рис. 2.13. Графическое определение радиуса кривизны траектории
Для этого прежде всего перейдем от дифференцирования по времени к дифференцированию по «пути»: 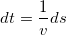 , имеем:
, имеем:
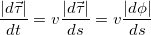
По определению производная 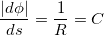 кривизне кривой C, а величина ей обратная равна радиусу кривизны кривой R. Собирая все вместе, для нормального ускорения
кривизне кривой C, а величина ей обратная равна радиусу кривизны кривой R. Собирая все вместе, для нормального ускорения 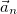 окончательно получаем:
окончательно получаем:
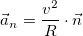 ,
,
где нормаль 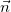 перпендикулярна к касательной
перпендикулярна к касательной 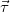 и всегда направлена к центру кривизны, см. рис. 11.
и всегда направлена к центру кривизны, см. рис. 11.
Game: Perform tasks and rest cool.3 people play!
Play game 1 и
1 и  2. Перпендикуляры к этим касательным пересекутся в некоторой точке O2. Заметим, что для кривой, не являющейся окружностью, расстояния R1 и R2 будут немного отличаться друг от друга. Если теперь точку 2 приближать к точке 1, пересечение перпендикуляров O2 будет перемещаться вдоль прямой O21 и в пределе окажется в некоторой точке O1. Расстояния R1 и R2 будут стремиться к общему пределу R, равному радиусу кривизны, а точка O1 и будет центром кривизны для точки 1. Действительно, окружность радиусом R с центром в 0 проходит через точку 1 и касается траектории (так как радиус ортогонален орту
2. Перпендикуляры к этим касательным пересекутся в некоторой точке O2. Заметим, что для кривой, не являющейся окружностью, расстояния R1 и R2 будут немного отличаться друг от друга. Если теперь точку 2 приближать к точке 1, пересечение перпендикуляров O2 будет перемещаться вдоль прямой O21 и в пределе окажется в некоторой точке O1. Расстояния R1 и R2 будут стремиться к общему пределу R, равному радиусу кривизны, а точка O1 и будет центром кривизны для точки 1. Действительно, окружность радиусом R с центром в 0 проходит через точку 1 и касается траектории (так как радиус ортогонален орту  1). Кроме того, по построению бесконечно близкая точка 2 также лежит на этой окружности. Таким образом, построенная окружность действительно «сливается» с траекторией в точке 1.
1). Кроме того, по построению бесконечно близкая точка 2 также лежит на этой окружности. Таким образом, построенная окружность действительно «сливается» с траекторией в точке 1.
Итак, в общем случае ускорение имеет две составляющие — тангенциальную
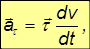
направленную вдоль касательной и определяющую скорость изменения модуля вектора скорости нормальную
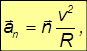
направленную перпендикулярно скорости к центру кривизны траектории и пропорциональную угловой скорости вращения вектора скорости при движении частицы вдоль криволинейной траектории (рис. 2.14).
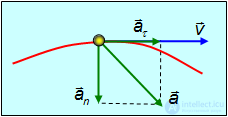
Рис. 2.14. Тангенциальное и нормальное ускорения при ускоренном криволинейном движении.
Game: Perform tasks and rest cool.3 people play!
Play game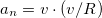 , где
, где 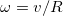 и есть угловая скорость вращения вектора скорости
и есть угловая скорость вращения вектора скорости 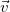 .
.
Полное ускорение
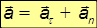
определяется по правилу параллелограмма. Модуль полного ускорения в соответствии с теоремой Пифагора равен
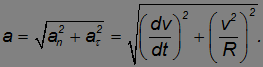
Выпишем без вывода формулы, связывающие радиус кривизны плоской траектории с координатами траектории. Если известна зависимость y = y(x), то
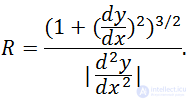
Если же траектория задана в параметрическом виде, x = x(t), y = y(t), то
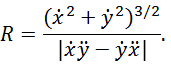
Пример криволинейного движения с постоянным ускорением (тело, брошенное под углом к горизонту) приведен на следующем рисунке:
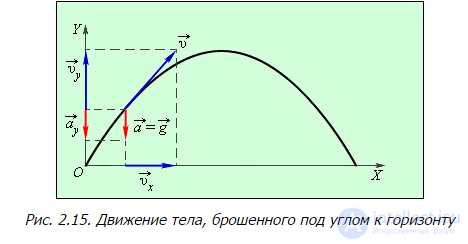
Рис. 2.15. Движение тела, брошенного под углом к горизонту
Рассмотрим в качестве примера применения выведенных формул движение тела, брошенного под углом 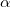 к горизонту в отсутствии сопротивления воздуха. Скажем, на горе, на высоте
к горизонту в отсутствии сопротивления воздуха. Скажем, на горе, на высоте 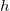 над уровнем моря стоит пушка, охраняющая прибрежные воды. Пусть снаряд выпускается под углом
над уровнем моря стоит пушка, охраняющая прибрежные воды. Пусть снаряд выпускается под углом 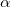 к горизонту с начальной скоростью
к горизонту с начальной скоростью 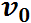 из точки
из точки 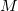 , положение которой определяется радиус-вектором
, положение которой определяется радиус-вектором 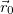 (рис. 2.16).
(рис. 2.16).
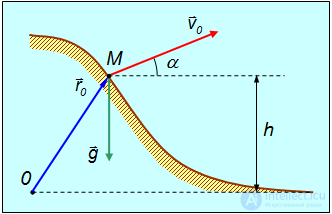
Рис. 2.16. Движение тела, брошенного под углом к горизонту
Дополнение.
Вывод уравнений движения материальной точки в поле силы тяжести
Напишем уравнение движения (уравнение второго закона Ньютона):
|
|
(2.7.1) |
Game: Perform tasks and rest cool.3 people play!
Play game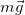 .
.
Масса тела в уравнении движения сокращается
|
|
(2.7.2) |
это означает, что тела — материальные точки — любых масс при одних и тех же начальных условиях будут двигаться в однородном поле тяжести одинаково. Спроектируем уравнение (2.7.2) на оси декартовой системы координат. Горизонтальная ось ОХ показана на рис. 13 пунктиром, ось OY проведем через точку О вертикально вверх, а горизонтальную ось OZ, также проходящую через точку О, направим перпендикулярно вектору 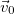 на нас. Получаем:
на нас. Получаем:
|
|
(2.7.3) |
Game: Perform tasks and rest cool.3 people play!
Play game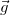 , поэтому его проекции на горизонтальные оси OX и OY равны нулю. Во втором уравнении учтено, что вектор
, поэтому его проекции на горизонтальные оси OX и OY равны нулю. Во втором уравнении учтено, что вектор 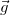 направлен вниз, а ось OY — вверх.
направлен вниз, а ось OY — вверх.
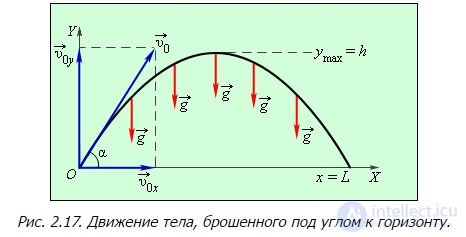
Рис. 2.17. Движение тела, брошенного под углом к горизонту.
Добавим к уравнениям движения начальные условия, которые определяют положение и скорость тела в начальный момент времени t0, пусть t0 = 0. Тогда, согласно рис. 2.7.4
|
|
(2.7.4) |
Или в проекциях на оси координат:
|
|
(2.7.5) |
Если производная некоторой функции равна нулю, то функция постоянна, соответственно из первого и третьего уравнений (2.7.3) получаем:
|
|
(2.7.6) |
Константы находятся из начальных условий, а именно: из первого и третьего уравнений (2.7.5) следует, что в любой момент времени
|
|
(2.7.7) |
Во втором уравнении (2.7.3) производная равна константе, откуда следует, что функция зависит от своего аргумента линейно, то есть
|
|
(2.7.8) |
Эта константа также находится из начальных условий. Подставляя в (2.7.8) t = 0 и сравнивая результат (vy(0) = const) cо вторым уравнением в (2.7.5) получаем
|
|
(2.7.9) |
Объединяя (2.7.7) и (2.7.9), получаем окончательные выражения для зависимостей проекций скорости на оси координат от времени:
|
|
(2.7.10) |
Game: Perform tasks and rest cool.3 people play!
Play gameДля определения зависимостей от времени координат тела необходимо выполнить еще одно интегрирование — проинтегрировать по времени уравнения (2.7.10) с учетом начальных условий (2.7.5). Используя ту же логику: если производная равна нулю, то функция постоянна, если производная постоянна, то функция зависит от своего аргумента линейно, и подбирая константы так, чтобы удовлетворить начальные условия, можно получить следующий результат:
|
|
(2.7.11) |
Третье уравнение (2.7.11) показывает, что траектория тела плоская, целиком лежит в плоскости XOY, это вертикальная плоскость, определяемая векторами 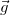 и
и 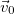 . Очевидно, что последнее утверждение общее: как бы ни были выбраны направления осей координат, траектория тела брошенного под углом к горизонту плоская, она всегда лежит в плоскости, определяемой вектором начальной скорости
. Очевидно, что последнее утверждение общее: как бы ни были выбраны направления осей координат, траектория тела брошенного под углом к горизонту плоская, она всегда лежит в плоскости, определяемой вектором начальной скорости 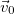 и вектором ускорения свободного падения
и вектором ускорения свободного падения 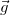 .
.
Game: Perform tasks and rest cool.3 people play!
Play game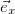 ,
, 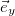 , и
, и 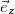 и сложить, а потом то же самое проделать с тремя уравнениями (2.7.11), то мы получим зависимости от времени вектора скорости частицы и ее радиус вектора. С учетом начальных условий имеем:
и сложить, а потом то же самое проделать с тремя уравнениями (2.7.11), то мы получим зависимости от времени вектора скорости частицы и ее радиус вектора. С учетом начальных условий имеем:
|
|
(2.7.12) |
|
|
(2.7.13) |
Формулы (2.7.12) и (2.7.13) можно было получить сразу, непосредственно из (2.7.2), если учесть, что ускорение свободного падения есть 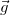 постоянный вектор. Если ускорение — производная от вектора скорости — постоянно, то вектор скорости зависит от времени линейно, а радиус-вектор, производная по времени от которого и есть линейно зависящий от времени вектор скорости, зависит от времени квадратично. Это и записано в соотношениях (2.7.12) и (2.7.13) с константами — постоянными векторами — подобранными соответственно начальным условиям в форме (2.7.4).
постоянный вектор. Если ускорение — производная от вектора скорости — постоянно, то вектор скорости зависит от времени линейно, а радиус-вектор, производная по времени от которого и есть линейно зависящий от времени вектор скорости, зависит от времени квадратично. Это и записано в соотношениях (2.7.12) и (2.7.13) с константами — постоянными векторами — подобранными соответственно начальным условиям в форме (2.7.4).
Из (2.7.13) в частности видно, что радиус-вектор является суммой трех векторов, складывающихся по обычным правилам, что наглядно показано на рис. 2.18.
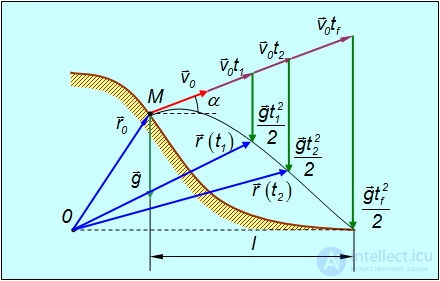
Рис. 2.18. Представление радиус-вектора r(t) в произвольный момент времени t в виде суммы трех векторов
Эти векторы представляют собой:
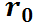 снаряда;
снаряда; (то есть как если бы сила тяжести отсутствовала);
(то есть как если бы сила тяжести отсутствовала);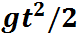 под действием силы тяжести (свободное падение в отсутствие начальной скорости).
под действием силы тяжести (свободное падение в отсутствие начальной скорости).Здесь отчетливо проявляется принцип независимости движений, известный в других областях физики как принцип суперпозиции (наложения). Вообще говоря, согласно принципу суперпозиции результирующий эффект нескольких воздействий представляет собой сумму эффектов от каждого воздействия в отдельности. Он является следствием линейности уравнений движения.
Видео 2.3. Независимость горизонтального и вертикального перемещений при движении в поле тяжести.
Поместим начало отсчета в точку бросания. Теперь 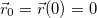 =0, оси, как и ранее, развернем так, чтобы ось 0x была горизонтальной, ось 0у — вертикальной, а начальная скорость
=0, оси, как и ранее, развернем так, чтобы ось 0x была горизонтальной, ось 0у — вертикальной, а начальная скорость 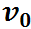 лежала в плоскости х0у (рис. 2.19).
лежала в плоскости х0у (рис. 2.19).
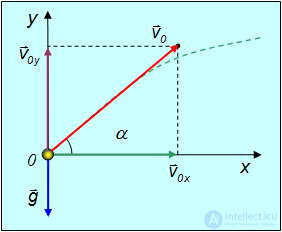
Рис. 2.19. Проекции начальной скорости на координатные оси
Спроецируем 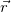 на оси координат (см.(2.7.11)):
на оси координат (см.(2.7.11)):
Game: Perform tasks and rest cool.3 people play!
Play game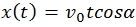
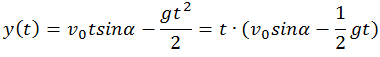
Траектория полета. Если из системы полученных уравнений исключить время t, то получим уравнение траектории:
|
|
(2.7.14) |
Это уравнение параболы, ветви которой направлены вниз.
Дальность полета при стрельбе с высоты h. В момент падения тела 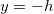 (снаряд попадает в цель, находящуюся на поверхности моря). Расстояние по горизонтали от пушки до цели равно при этом
(снаряд попадает в цель, находящуюся на поверхности моря). Расстояние по горизонтали от пушки до цели равно при этом 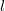 . Подставляя
. Подставляя 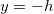 ;
;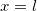 в уравнение траектории, получаем квадратное уравнение для дальности полета
в уравнение траектории, получаем квадратное уравнение для дальности полета 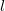 :
:
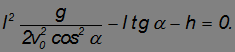
Game: Perform tasks and rest cool.3 people play!
Play game|
|
(2.7.15) |
При 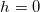 отсюда получается известная формула школьного курса физики
отсюда получается известная формула школьного курса физики
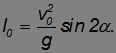
Из нее следует, в частности, что максимальная дальность полета
|
|
(2.7.16) |
достигается при 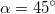 , если h = 0.
, если h = 0.
Максимальная дальность полета. При выстреле с горы высотой 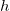 это уже не так. Найдем угол
это уже не так. Найдем угол  , при котором достигается максимальная дальность полета. Зависимость дальности полета
, при котором достигается максимальная дальность полета. Зависимость дальности полета 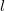 от угла
от угла 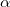 достаточно сложна, и вместо дифференцирования для нахождения максимума мы поступим следующим образом. Представим себе, что мы увеличиваем начальный угол
достаточно сложна, и вместо дифференцирования для нахождения максимума мы поступим следующим образом. Представим себе, что мы увеличиваем начальный угол 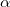 . Сначала дальность полета растет (см. формулу (2.7.15)), достигает максимального значения
. Сначала дальность полета растет (см. формулу (2.7.15)), достигает максимального значения 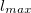 и снова начинает падать (до нуля при выстреле вертикально вверх). Таким образом, для каждой дальности полета, кроме максимальной, соответсвует два направления начальной скорости.
и снова начинает падать (до нуля при выстреле вертикально вверх). Таким образом, для каждой дальности полета, кроме максимальной, соответсвует два направления начальной скорости.
Обратимся снова к квадратному уравнению относительности дальности полета 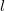 и рассмотрим его как уравнение для угла
и рассмотрим его как уравнение для угла 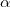 . Учитывая, что
. Учитывая, что
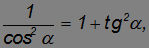
перепишем его в виде:
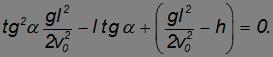
Мы снова получили квадратное уравнение, на этот раз — для неизвестной величины 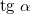 . Уравнение имеет два корня, что соответствует двум углам, при которых дальность полета равна
. Уравнение имеет два корня, что соответствует двум углам, при которых дальность полета равна 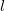 . Но когда
. Но когда 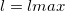 , оба корня должны совпасть. Это означает, что равен нулю дискриминант квадратного уравнения:
, оба корня должны совпасть. Это означает, что равен нулю дискриминант квадратного уравнения:
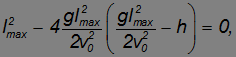
откуда следует результат
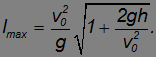
При 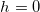 этот результат воспроизводит формулу (2.7.16)
этот результат воспроизводит формулу (2.7.16)
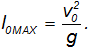
Game: Perform tasks and rest cool.3 people play!
Play game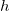 много меньше дальности полета
много меньше дальности полета 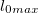 на равнине. При
на равнине. При 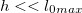 квадратный корень может быть аппроксимирован первыми членами разложения в ряд Тейлора и мы получаем приближенное выражение
квадратный корень может быть аппроксимирован первыми членами разложения в ряд Тейлора и мы получаем приближенное выражение
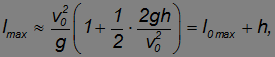
то есть дальность выстрела увеличивается примерно на высоту подъема пушки.
Когда l = lmax, и a = amax, как уже отмечалось, дискриминант квадратного уравнения равен нулю, соответственно, его решение имеет вид:
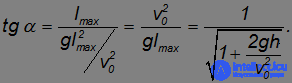
Поскольку тангенс меньше единицы, угол, при котором достигается максимальная дальность полета, меньше 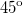 .
.
Максимальная высота подъема над начальной точкой. Эта величина может быть определена из равенства нулю вертикальной составляющей скорости в верхней точке траектории
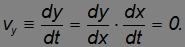
Game: Perform tasks and rest cool.3 people play!
Play game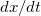 не равна нулю, поэтому
не равна нулю, поэтому
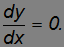
Дифференцируя ранее полученное уравнение траектории, приходим к уравнению:
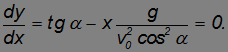
Отсюда
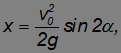
что при подстановке в уравнение траектории полета приводит к формуле:
|
|
(2.7.17) |
Продолжительность полета. Поскольку горизонтальная составляющая скорости не меняется, то продолжительность полета 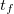 определяется как отношение дальности полета к горизонтальной составляющей начальной скорости, то есть
определяется как отношение дальности полета к горизонтальной составляющей начальной скорости, то есть
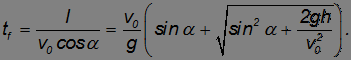
При 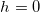 получаем
получаем
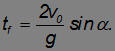
При 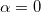 (пушка стреляет в горизонтальном направлении) время полета
(пушка стреляет в горизонтальном направлении) время полета
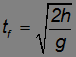
равно времени падения тела с высоты 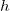 . Дальность полета при этом
. Дальность полета при этом
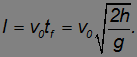
Путь, пройденный телом. За время t тело проходит путь
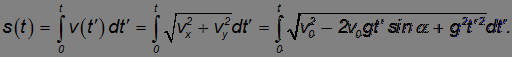
Интеграл берется в элементарных функциях, но из-за громоздкости ответа мы не выписываем здесь соответствующее выражение.
Расстояние от места выстрела. К моменту времени t расстояние от места выстрела определяется модулем радиус-вектора:
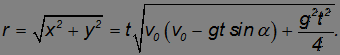
Game: Perform tasks and rest cool.3 people play!
Play game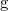 , которое и является полным ускорением.
, которое и является полным ускорением.
Тангенциальная компонента ускорения, характеризующая быстроту изменения модуля скорости, равна
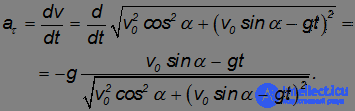
Нормальная компонента ускорения, изменяющая направление скорости тела, определяется соотношением:
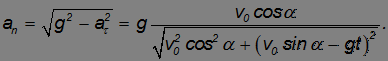
Используя связь нормальной компоненты ускорения с радиусом кривизны, находим 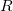 :
:
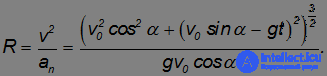
В числителе этого выражения в степени 3/2 стоит модуль скорости. Поэтому, даже не вычисляя производной, мы можем ответить на вопрос, в какой точке траектории кривизна максимальна, а радиус кривизны C = 1/R минимален. Радиус кривизны R достигает минимума там, где минимальна скорость, а это имеет место в верхней точке траектории, в которой вертикальная компонента скорости равна нулю:
Game: Perform tasks and rest cool.3 people play!
Play game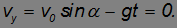
Еще раз напомним, что горизонтальная компонента скорости, всюду имеет одно и то же значение. В верхней точке модуль скорости равен горизонтальной составляющей скорости

поэтому
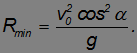
Для сравнения: радиус кривизны 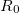 в начальный момент
в начальный момент 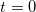 равен
равен
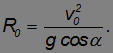
Положение центра кривизны (для высшей точки траектории). По определению радиуса кривизны центр кривизны для высшей точки траектории находится прямо под этой точкой на высоте
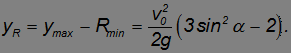
Напомним, что мы отсчитываем вертикальные расстояния от уровня пушки, а не от уровня моря.
При
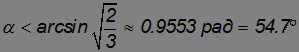
эта координата отрицательна, то есть центр кривизны находится ниже пушки. Максимально высокое положение центр кривизны занимает при 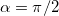 :
:
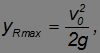
что совпадает с верхней точкой траектории. Тогда радиус кривизны равен нулю. Это значит, что кривизна в этой точке бесконечна, в чем легко убедиться, представив себе траекторию при вертикальном движении снаряда.
Рассмотрим кинематику движения протяженного тела, размерами которого в условиях рассматриваемой задачи пренебречь нельзя. Тело будем считать недеформируемым, другими словами, — абсолютно твердым.
Движение, при котором любая прямая, связанная с движущимся телом, остается параллельной самой себе, называется поступательным.
Game: Perform tasks and rest cool.3 people play!
Play gameПоступательное движение абсолютно твердого тела можно охарактеризовать движением какой-либо точки этого тела, так как при поступательном движении все точки тела движутся с одними и теми же скоростями и ускорениями, а траектории их движения конгруэнтны. Определив движение какой-нибудь из точек твердого тела, мы вместе с тем определим движение всех остальных его точек. Поэтому при описании поступательного движения не возникает новых проблем по сравнению с кинематикой материальной точки. Пример поступательного движения показан на рис. 2.20.
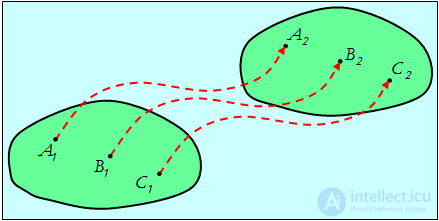
Рис.2.20. Поступательное движение тела
Пример поступательного движения показан на следующем рисунке:
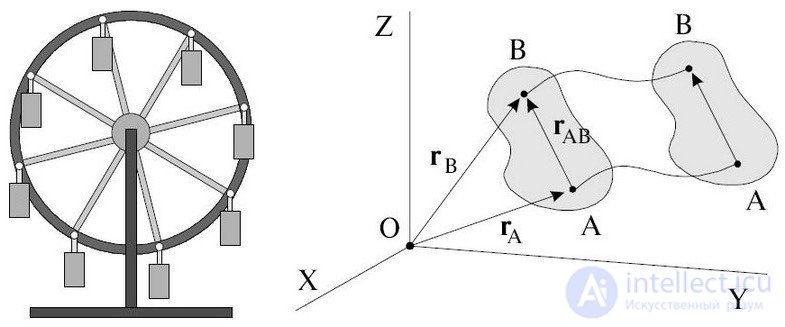
Рис.2.21. Плоское движение тела
Game: Perform tasks and rest cool.3 people play!
Play gameДвижение, при котором две точки тела остаются неподвижными, называется вращением вокруг неподвижной оси.
Прямая, соединяющая эти точки, также неподвижна и называется осью вращения.
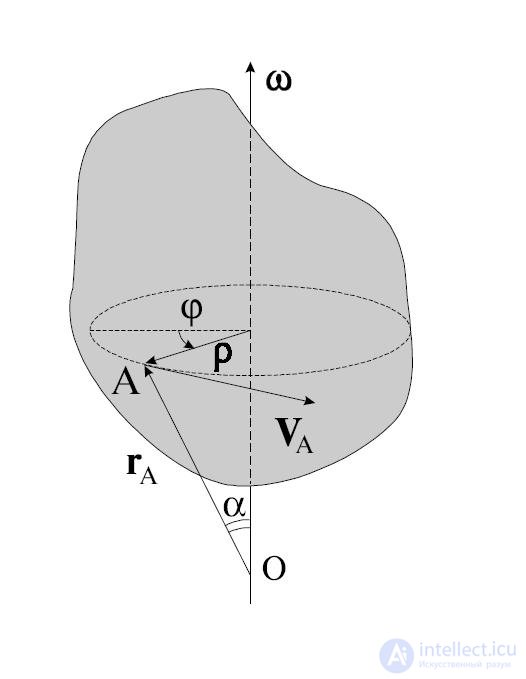
Рис.2.22. Вращение твердого тела
При таком движении все точки тела движутся по окружностям, расположенным в плоскостях, перпендикулярных оси вращения. Центры окружностей лежат на оси вращения. При этом ось вращения может находиться и вне тела.
Видео 2.4. Поступательное и вращательное движения.
Угловая скорость, угловое ускорение. При вращении тела вокруг какой-либо оси все его точки описывают окружности различного радиуса и, следовательно, имеют различные перемещения, скорости и ускорения. Тем не менее, можно описать вращательное движение всех точек тела одинаковым образом. Для этого используют иные (по сравнению с материальной точкой) кинематические характеристики движения — угол поворота 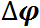 , угловую скорость
, угловую скорость 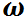 , угловое ускорение
, угловое ускорение 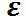 .
.
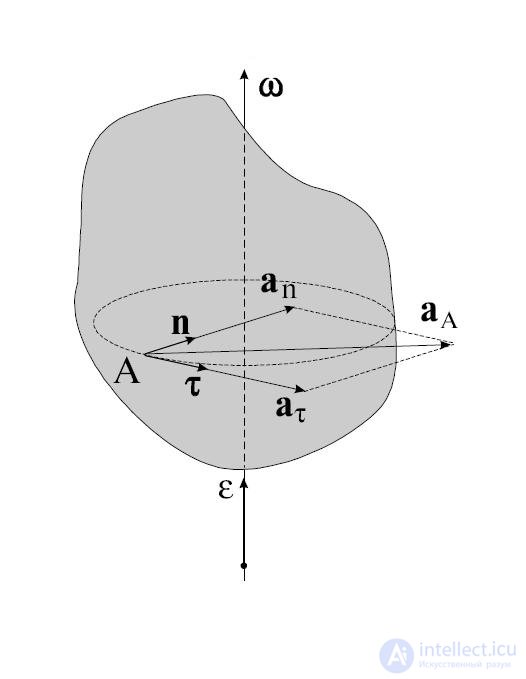
Рис. 2.23. Вектора ускорения точки, движущейся по окружности
Роль перемещения 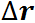 при вращательном движении играет вектор малого поворота
при вращательном движении играет вектор малого поворота 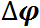 , вокруг оси вращения 00' (рис. 2.24.). Он будет одинаков для любой точки абсолютно твердого тела (например, точек 1, 2, 3 ).
, вокруг оси вращения 00' (рис. 2.24.). Он будет одинаков для любой точки абсолютно твердого тела (например, точек 1, 2, 3 ).
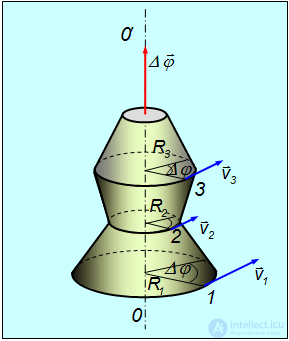
Рис. 2.24. Вращение абсолютно твердого тела вокруг неподвижной оси
Модуль вектора поворота равен величине угла поворота 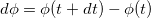 причем угол измеряется в радианах.
причем угол измеряется в радианах.
Направлен вектор бесконечно малого поворота по оси вращения в сторону движения правого винта (буравчика), вращаемого в том же направлении, что и тело.
Видео 2.5. Конечные угловые перемещения — не векторы, так как не складываются по правилу параллелограмма. Бесконечно малые угловые перемещения – векторы.
Game: Perform tasks and rest cool.3 people play!
Play gameОтношение вектора бесконечно малого поворота ко времени, за которое этот поворот имел место
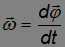
называется угловой скоростью вращения.
Основной единицей измерения величины угловой скорости является рад/с. В печатных изданиях, по причинам никакого отношения к физике не имеющим, нередко пишут 1/с или с-1, что, строго говоря, неверно. Угол — величина безразмерная, но единицы его измерения различны (градусы, румбы, грады …) и их необходимо указывать, хотя бы во избежание недоразумений.
Видео 2.6. Стробоскопический эффект и его использование для дистанционного измерения угловой скорости вращения.
Game: Perform tasks and rest cool.3 people play!
Play game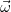 как и вектор
как и вектор 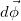 , которому она пропорциональна, является аксиальным вектором. При вращении вокруг неподвижной оси угловая скорость не меняет своего направления. При равномерном вращении остается постоянной и ее величина, так что вектор
, которому она пропорциональна, является аксиальным вектором. При вращении вокруг неподвижной оси угловая скорость не меняет своего направления. При равномерном вращении остается постоянной и ее величина, так что вектор 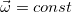 . В случае достаточного постоянства во времени величины угловой скорости вращение удобно охарактеризовать его периодом Т :
. В случае достаточного постоянства во времени величины угловой скорости вращение удобно охарактеризовать его периодом Т :
Период вращения — это время, за которое тело совершает один оборот (поворот на угол 2π) вокруг оси вращения.
Слова «достаточного постоянства» означают, очевидно, что за период (время одного оборота) модуль угловой скорости меняется несущественно.
Часто используют также число оборотов в единицу времени
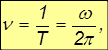
откуда
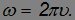
При этом в технических приложениях (прежде всего, всякого рода двигатели) в качестве единицы времени общепринято брать не секунду, а минуту. То есть угловая скорость вращения 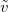 указывается в оборотах в минуту. Как легко видеть, связь между
указывается в оборотах в минуту. Как легко видеть, связь между  (в радианах в секунду) и
(в радианах в секунду) и 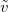 (в оборотах в минуту) следующая
(в оборотах в минуту) следующая
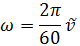
Направление вектора угловой скорости показано на рис. 2.25.
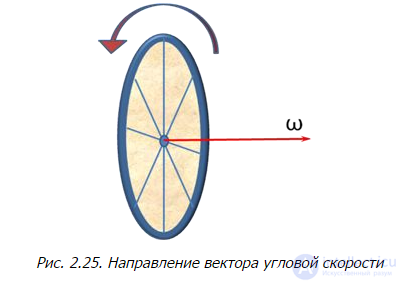
Рис. 2.25. Направление вектора угловой скорости
По аналогии с линейным ускорением вводится угловое ускорение 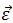 как скорость изменения вектора угловой скорости. Угловое ускорение также является аксиальным вектором (псевдовектором).
как скорость изменения вектора угловой скорости. Угловое ускорение также является аксиальным вектором (псевдовектором).
Угловое ускорение 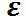 — аксиальный вектор, определяемый как производная по времени от угловой скорости
— аксиальный вектор, определяемый как производная по времени от угловой скорости
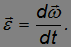
При вращении вокруг неподвижной оси, в более общем случае при вращении вокруг оси, которая остается параллельной самой себе, вектор угловой скорости также направлен параллельно оси вращения. При возрастании величины угловой скорости |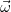 | угловое ускорение совпадает с ней по направлению, при убывании — направлено в противоположную сторону. Подчеркнем, что это лишь частный случай неизменности направления оси вращения, в общем случае (вращение вокруг точки) ось вращения сама поворачивается и тогда сказанное выше неверно.
| угловое ускорение совпадает с ней по направлению, при убывании — направлено в противоположную сторону. Подчеркнем, что это лишь частный случай неизменности направления оси вращения, в общем случае (вращение вокруг точки) ось вращения сама поворачивается и тогда сказанное выше неверно.
Game: Perform tasks and rest cool.3 people play!
Play game , направленной по касательной к соответствующей окружности (см. рис. 19). Пусть материальная точка вращается вокруг оси 00' по окружности радиусом R. За малый промежуток времени
, направленной по касательной к соответствующей окружности (см. рис. 19). Пусть материальная точка вращается вокруг оси 00' по окружности радиусом R. За малый промежуток времени 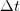 она пройдет путь
она пройдет путь 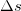 , соответствующий углу поворота
, соответствующий углу поворота 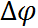 . Тогда
. Тогда
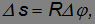
Переходя к пределу 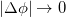 , получим выражение для модуля линейной скорости точки вращающегося тела.
, получим выражение для модуля линейной скорости точки вращающегося тела.
Напомним, здесь R — расстояние от рассматриваемой точки тела до оси вращения.
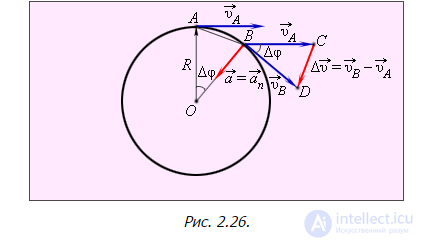
Рис. 2.26.
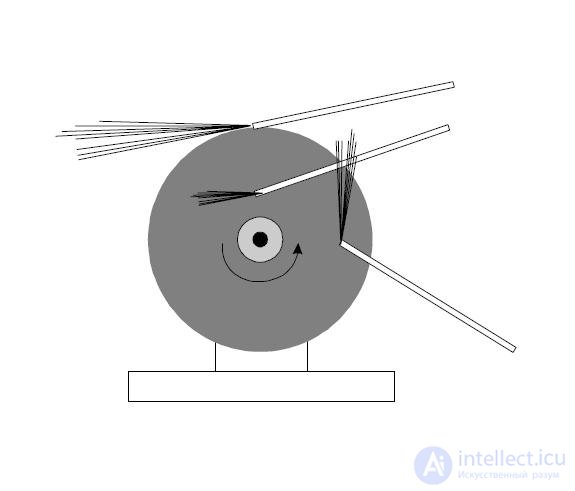
Рис. 2.27. Направление движения искр при заточке инструментов.
Так как нормальное ускорение равно
Game: Perform tasks and rest cool.3 people play!
Play game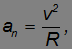
то с учетом соотношения для угловой и линейной скорости получаем
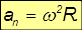
Нормальное ускорение точек вращающегося твердого тела часто называют центростремительным ускорением.
Дифференцируя по времени выражение для  , находим
, находим
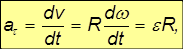
где 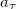 — тангенциальное ускорение точки, движущейся по окружности радиусом R.
— тангенциальное ускорение точки, движущейся по окружности радиусом R.
Таким образом, как тангенциальное, так и нормальное ускорения растут линейно с ростом радиуса R — расстояния от оси вращения. Полное ускорение также линейно зависит от R :
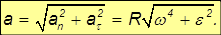
Пример. Найдем линейную скорость  и центростремительное ускорение
и центростремительное ускорение 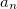 точек, лежащих на земной поверхности на экваторе и на широте Москвы (
точек, лежащих на земной поверхности на экваторе и на широте Москвы (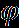 = 56°). Мы знаем период вращения Земли вокруг собственной оси Т = 24 часа = 24х60х60 = 86 400 с. Отсюда находится угловая скорость вращения
= 56°). Мы знаем период вращения Земли вокруг собственной оси Т = 24 часа = 24х60х60 = 86 400 с. Отсюда находится угловая скорость вращения
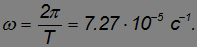
Средний радиус Земли
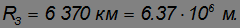
Расстояние до оси вращения на широте 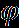 равно
равно
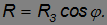
Отсюда находим линейную скорость
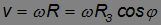
и центростремительное ускорение
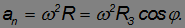
На экваторе 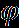 = 0, cos
= 0, cos 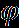 = 1, следовательно,
= 1, следовательно,
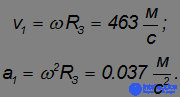
Game: Perform tasks and rest cool.3 people play!
Play game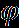 = cos 56° = 0,559 и получаем:
= cos 56° = 0,559 и получаем:
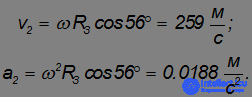
Мы видим, что влияние вращения Земли не столь велико: отношение центростремительного ускорения на экваторе к ускорению свободного падения равно
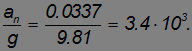
Тем не менее, как мы увидим в дальнейшем, эффекты вращения Земли вполне наблюдаемы.
Связь между векторами линейной и угловой скорости. Полученные выше соотношения между угловой и линейной скоростью записаны для модулей векторов  и
и  . Чтобы записать эти соотношения в векторном виде, используем понятие векторного произведения.
. Чтобы записать эти соотношения в векторном виде, используем понятие векторного произведения.
Пусть 0z — ось вращения абсолютно твердого тела (рис. 2.28).
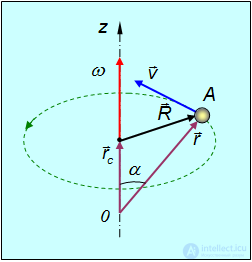
Game: Perform tasks and rest cool.3 people play!
Play gameТочка А вращается по окружности радиусом R. R — расстояние от оси вращения до рассматриваемой точки тела. Примем точку 0 за начало координат. Тогда
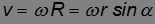
и так как

то по определению векторного произведения, для всех точек тела
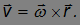
Здесь 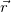 — радиус-вектор точки тела, начинающийся в точке О, лежащей в произвольном фиксированном месте, обязательно на оси вращения
— радиус-вектор точки тела, начинающийся в точке О, лежащей в произвольном фиксированном месте, обязательно на оси вращения
Но, с другой стороны
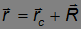
и
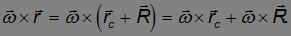
Первое слагаемое равно нулю, так как векторное произведение коллинеарных векторов равно нулю. Следовательно,
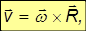
где вектор R перпендикулярен оси вращения и направлен от нее, а его модуль равен радиусу окружности, по которой движется материальная точка и начинается этот вектор в центре этой окружности.
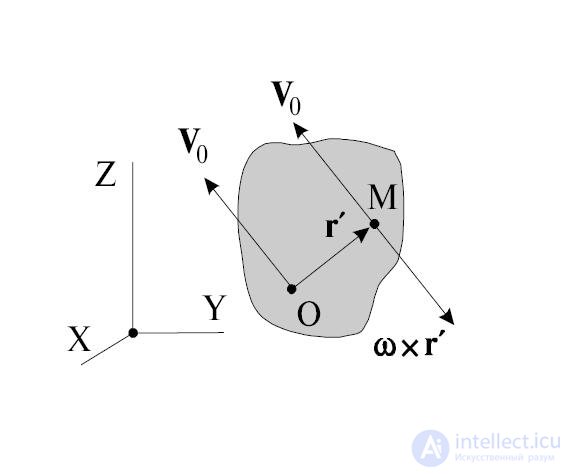
Рис. 2.29. К определению мгновенной оси вращения
Нормальное (центростремительное) ускорение также можно записать в векторной форме:
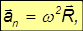
причем знак «–» показывает, что оно направлено к оси вращения. Дифференцируя соотношение для линейной и угловой скорости по времени, находим для полного ускорения выражение
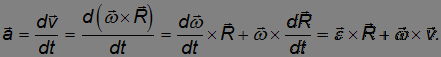
Game: Perform tasks and rest cool.3 people play!
Play game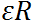 , поскольку
, поскольку
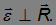
Сравнивая с выражением для тангенциального ускорения, приходим к выводу, что это — вектор тангенциального ускорения
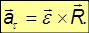
Следовательно, второе слагаемое представляет собой нормальное ускорение этой же точки:
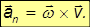
Действительно, оно направлено вдоль радиуса R к оси вращения и его модуль равен
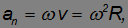
так как
Game: Perform tasks and rest cool.3 people play!
Play game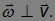
Поэтому данное соотношение для нормального ускорения является другой формой записи ранее полученной формулы.
Исследование, описанное в статье про кинематика, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое кинематика, вращение абсолютно твердого тела, движение тела брошенного под углом к горизонту, ускорение тела и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Физические основы механики
Комментарии
Оставить комментарий
Физические основы механики
Термины: Физические основы механики