Лекция
Привет, Вы узнаете о том , что такое динамика материальной точки, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое динамика материальной точки, принцип инерции галилея, законы ньютона, механические силы, закон сохранения импульса, реактивное движение, принцип относительности галилея , настоятельно рекомендую прочитать все из категории Физические основы механики.
Динамика исследует законы и причины, вызывающие движение тел, то есть изучает движение материальных тел под действием приложенных к ним сил. Механика — одна из древнейших наук, развитие которой стимулировалось практикой, нуждами общества. К первым теоретическим трактатам по механике относятся «Физика» и «Механика» Аристотеля (IV в. до н.э.). Научные основы статики (теория рычага, учение о центре тяжести, начала гидростатики) разработал Архимед (III в. до н.э.). Дальнейшее развитие механики (сложение сил по правилу параллелограмма, учение о моменте силы) связано с именами итальянца Леонардо да Винчи (ХV в.), фламандца Симона Стевина (ХVI в.) и других ученых. Основу современной классической механики составляют три закона Ньютона. Механика Ньютона базируется на основополагающих принципах Галилея.
Г. Галилей (1564–1642) справедливо считается основателем физики как науки. Ему мы обязаны развитием современного метода исследований, кратко выражающегося в цепочке: эксперимент => модель (выделение в явлении главных особенностей, то есть применение абстракции) => математическое описание => следствия модели => новый эксперимент для их проверки.
Среди прочих научных достижений, в механике им были введены два основополагающих принципа: принцип инерции и принцип относительности. Принцип инерции Галилея был повторен И. Ньютоном (1643–1727) в качестве первого закона механики.
Первый закон Ньютона гласит:
Существуют такие системы отсчета, в которых всякая материальная точка находится в состоянии покоя или равномерного прямолинейного движения до тех пор, пока это состояние не будет изменено воздействием со стороны других тел. Такие системы отсчета принято называть инерциальными.
Ответ на вопрос: «Существуют ли инерциальные системы отсчета или нет?», как всегда, дает эксперимент. По результатам современных измерений гелиоцентрическая система отсчета, в которой неподвижен центр Солнца, и оси которой направлены на неподвижные звезды, является инерциальной. Это означает следующую простую вещь: существующие акселерометры (измерители ускорения) не обнаруживают отклонений от первого закона Ньютона в гелиоцентрической системе отсчета. Покой или равномерное прямолинейное движение — это состояние с равным нулю ускорением, следовательно, если тело, не подверженное воздействиям извне, приобретает ускорение, то это означает, что движение этого тела рассматривается в неинерциальной системе отсчета. Солнечная система совершает финитное движение в пределах нашей галактики (Млечный путь), любое финитное движение есть движение с ускорением, но солнечная система далека от центра галактики — мы периферийные жители — кривизна ее траектории ничтожна, наши приборы не обнаруживают ускорений и мы утверждаем, что гелиоцентрическая система отсчета инерциальна. Инерциальная система отсчета — еще одна идеализация: в точном смысле инерциальных систем отсчета не существует. Естественно предположить, что это обстоятельство было в ряду тех, что подвигли Эйнштейна на создание общей теории относительности, в которой утверждается физическое равноправие всех вообще, а не только инерциальных, систем отсчета, а поля сил инерции эквивалентны гравитационным полям (так называемый «принцип эквивалентности» подробнее речь об этом пойдет позже).
Свойство тела сохранять состояние покоя или прямолинейного равномерного движения называется инерцией. Сам этот принцип — принцип инерции Галилея (или первый закон Ньютона) — далеко не столь очевиден.
До Галилея думали, что для движения нужна какая-то причина, движущая сила. Даже великий Леонардо да Винчи писал: «Всякое движение стремится к своему сохранению, или же каждое движущееся тело движется постоянно, пока в нем сохраняется действие его двигателя». Удивительно, но туповатый полковник фон Циллергут из книги Я. Гашека «Похождения бравого солдата Швейка», мыслил похоже: нет бензина, не работает двигатель, автомобиль останавливается. После Галилея стала возможной чеканная латинская формулировка Р. Декарта (1596–1650): «Quod in vacuo movetur, semper moveri» (что движется в пустоте, будет двигаться всегда).
Дело в том, что в природе действительно никогда не наблюдаются тела, вечно сохраняющие состояние покоя или прямолинейного равномерного движения. Нужно было проявить ту самую способность строить модели, отбрасывать несущественное, абстрагироваться, чтобы открыть принцип инерции. Изучая основные законы механики, мы идеализируем систему: пренебрегаем силами трения, считаем, что поблизости нет других тел и т. д. И тогда принцип инерции проявляет себя во всей своей красе и силе:
Для равномерного прямолинейного движения не нужно двигателя, движущая сила нужна для изменения такого вида движения тела.
Для описания воздействия вводят понятие силы. Под действием сил тела либо изменяют скорость движения 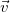 , то есть приобретают ускорения (динамическое проявление сил), либо деформируются, то есть изменяют свою форму и размеры (статическое проявление сил). В каждый момент времени сила характеризуется числовым значением, направлением в пространстве и точкой приложения.
, то есть приобретают ускорения (динамическое проявление сил), либо деформируются, то есть изменяют свою форму и размеры (статическое проявление сил). В каждый момент времени сила характеризуется числовым значением, направлением в пространстве и точкой приложения.
Сила — результат и проявление взаимодействия. Это векторная величина,являющаяся в классической(не квантовой) физике количественной характеристикой взаимодействия.
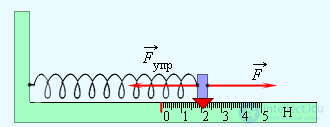
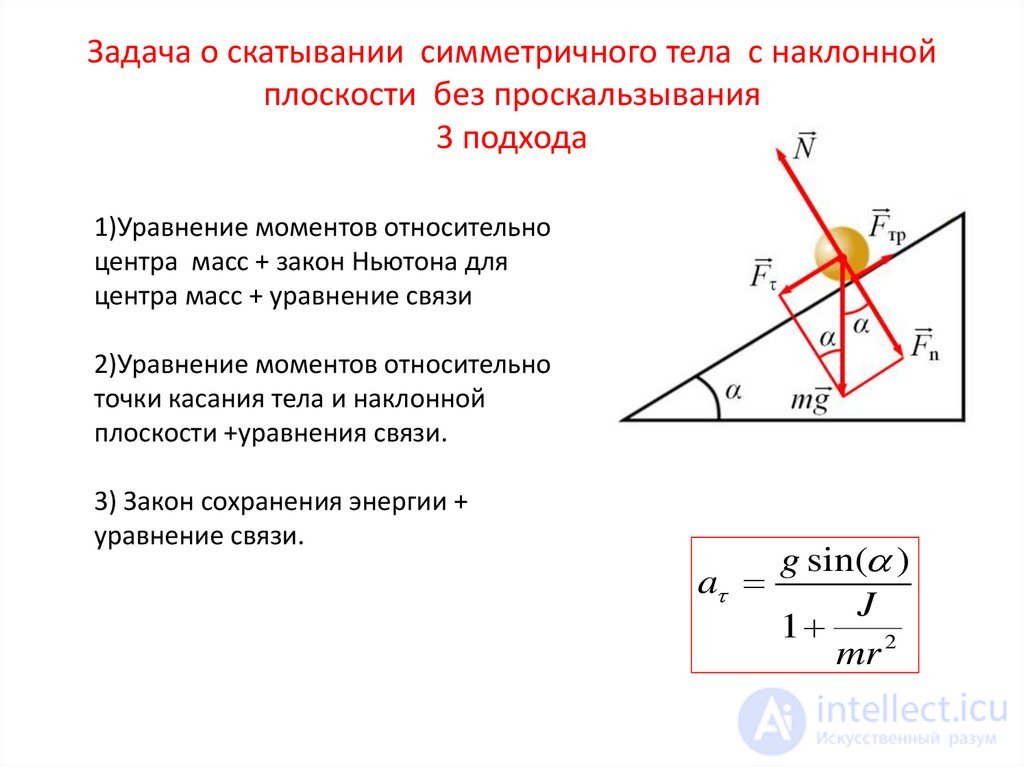
Рис. 3.1. Сила, действующая на пружину
Для того, чтобы установить, какие силы действуют на тело, необходимо определить, с какими другими телами взаимодействует данное тело. Сила всегда есть результат взаимодействия физических тел. Наверное по этой причине Р. Фейнман в своих «Фейнмановских лекциях по физике» назвал силы инерции, не являющиеся результатом взаимодействия рассматриваемого тела с другими телами и появляющиеся только в неинерциальных системах отсчета, псевдосилами.
задача о соскальзывании тела с наклонной плоскости.
Из опыта известно, что при одинаковых воздействиях различные тела неодинаково изменяют скорость своего движения, то есть, иными словами, приобретают различные ускорения, поэтому в уравнение, связывающее силу, действующую на тело, и его ускорение должна входить некоторая характеристика самого тела. Такой характеристикой является масса тела m.
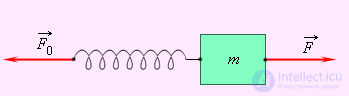
Рис. 3.2. Две различных силы, действующих на тело, вызывают его ускорение.
Установленный экспериментально второй закон Ньютона утверждает:
Произведение массы материальной точки на ее ускорение равно векторной сумме сил, приложенных к этой точке:
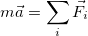
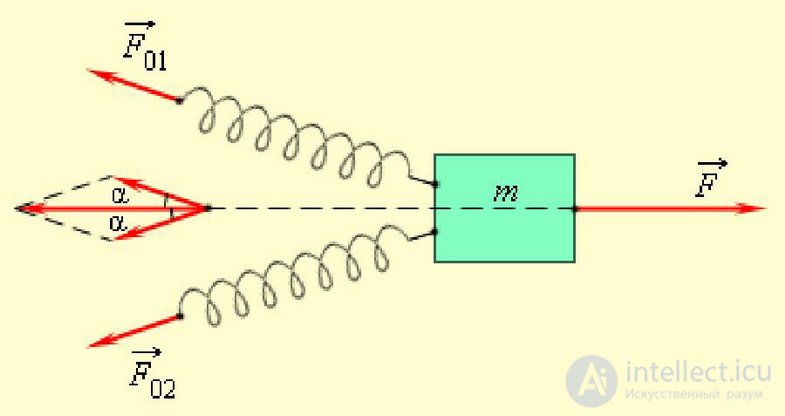
Рис. 3.3. Несколько сил, действующих на тело, могут нейтрализовывать друг друга.
Сразу подчеркнем, что это справедливо только при нерелятивистских скоростях движения, то есть скоростях малых по сравнению со скоростью света в вакууме: 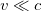 .
.
Второй закон Ньютона нередко формулируется так. Произведение массы тела на его ускорение равно векторной сумме сил, приложенных к телу.

Рис. 3.4. Только внешние силы вызывают ускорение системы (в данном случае — две тележки с грузами.)
Необходимо оговорить, что в такой формулировке, если речь идет о протяженном теле, которое нельзя считать материальной точкой, второй закон Ньютона описывает только поступательное движение протяженного тела, при котором все точки тела имеют одинаковые ускорения, скорости и перемещения. Вращательное движение тела в таком виде — второй закон Ньютона описать не в состоянии. Вращение протяженного тела кардинальным образом зависит от того, в каких его точках приложены силы к телу. Очевидно, что в случае материальной точки этот вопрос лишен смысла: все силы приложены к этой точке. В написанном выше уравнении, а именно:
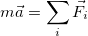
нет никаких указаний на то, каковы точки приложения сил к протяженному телу.
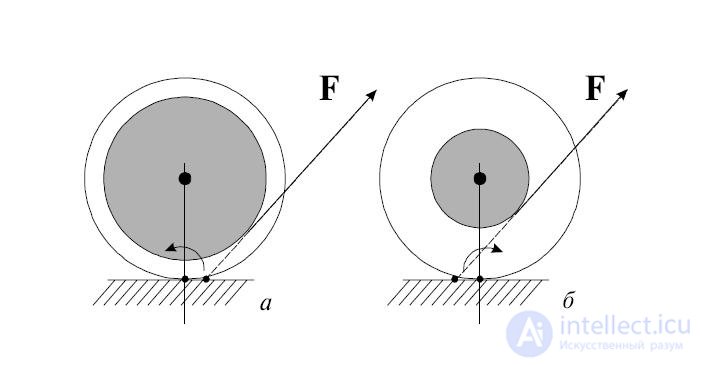
Рис. 3.5. Движение катушки зависит не только от приложенных сил, но и точек их приложения.
Для описания вращательного движения протяженного тела написанное выше уравнение второго закона Ньютона модифицируется так, чтобы в нем в явном виде присутствовали радиус-векторы точек приложения сил. В результате такой модификации в правой части уравнения вместо сил появляются моменты сил.
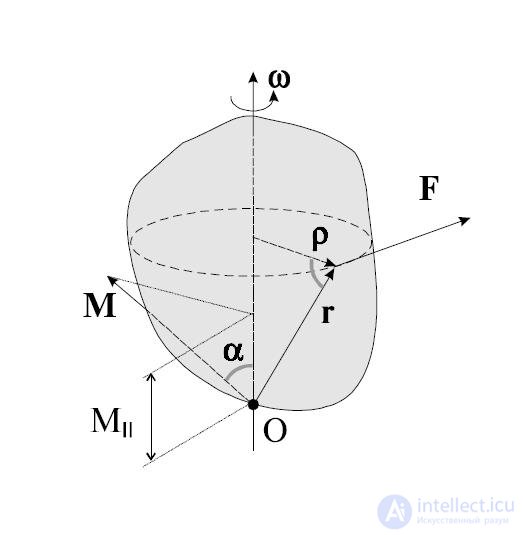
Рис. 3.6. Вращение тела вокруг неподвижной оси.
Учитывая, что ускорение 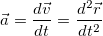 , второй закон Ньютона можно записать в виде трех полностью
, второй закон Ньютона можно записать в виде трех полностью
эквивалентных друг другу соотношений:
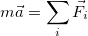
(3.2.1)
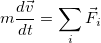
(3.2.2)
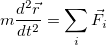
(3.2.3)
каждое из которых позволяет подчеркнуть какой-то из аспектов этого закона.
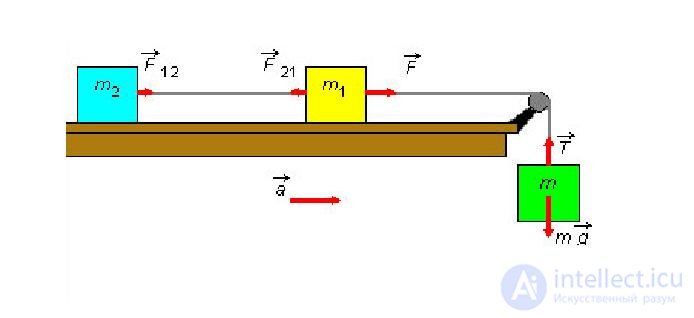
Рис. 3.7. Силы,возникающие при ускоренном движении системы.
Начнем с достаточно тривиальных обстоятельств.
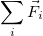 обозначить
обозначить 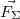
и вспомнить, что сила может быть нестационарной, то есть зависеть от времени, что в большинстве случаев силовые поля неоднородны, то есть сила зависит от координат точки и, что есть такие силы, как например, сила жидкого трения, которая зависит от скорости движения тела в жидкости, то получается, что в общем случае 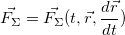 .
.
Тогда, из (3.2.3) вытекает, что
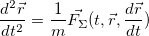
(3.2.4)
уравнение второго закона Ньютона есть дифференциальное уравнение второго порядка, разрешенное относительно старшей (второй) производной.
Именно по этой причине уравнение второго закона Ньютона чаще всего называют уравнением движения.
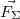 — решение уравнения (3.2.4) существует. Отметим, что в физических приложениях эти требования практически всегда выполнены, а если нет, то есть смысл проверить, корректна ли, не слишком ли идеализирована постановка физической задачи. Во-вторых, решений уравнения (3.2.4) бесконечно много и отличаются эти решения значениями двух (уравнение второго порядка) векторных констант, для нахождения которых необходимы начальные условия: необходимо указать начальное положение точки и ее начальную скорость в некоторый начальный момент времени t0
— решение уравнения (3.2.4) существует. Отметим, что в физических приложениях эти требования практически всегда выполнены, а если нет, то есть смысл проверить, корректна ли, не слишком ли идеализирована постановка физической задачи. Во-вторых, решений уравнения (3.2.4) бесконечно много и отличаются эти решения значениями двух (уравнение второго порядка) векторных констант, для нахождения которых необходимы начальные условия: необходимо указать начальное положение точки и ее начальную скорость в некоторый начальный момент времени t0
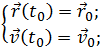
(3.2.5)
В математике доказано, что решение дифференциальной задачи (3.2.4) — (3.2.5) единственно. Доказанная единственность решения весьма полезна с чисто практической точки зрения: как бы не была найдена функция, обращающая в тождество уравнение (3.2.4) и удовлетворяющая начальным условиям (3.2.5) — это то единственное решение, которое имеет данная задача.
Запись второго закона Ньютона в виде (3.2.2) подсказывает введение новой кинематической характеристики движущейся материальной точки, учитывающей не только ее скорость 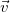 , но и массу m. Если масса постоянна, а это именно так — читайте дальше, то ее можно ввести под знак производной и переписать уравнение движения в виде
, но и массу m. Если масса постоянна, а это именно так — читайте дальше, то ее можно ввести под знак производной и переписать уравнение движения в виде

(3.2.6)
Здесь
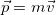
(3.2.7)
по определению по определению, есть импульс материальной точки массы m, движущейся с нерелятивистской скоростью 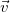 , последнее означает (напомним), что
, последнее означает (напомним), что 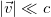 .
.
Релятивистские ограничения применимости ньютоновской механики вообще, и выражения для импульса (3.2.7), в частности, были поняты, разумеется, не во времена Ньютона, а только после создания Эйнштейном специальной теории относительности, которую в данном контексте, разумеется, можно трактовать как механику околосветовых скоростей, когда  .
.
На сегодняшний день (начало 2010 года) исчерпывающего ответа на вопрос, что такое масса не существует. Для решения, в частности и этого вопроса, был построен и ныне испытывается в действии БАК — большой адронный коллайдер.
Сегодня, для наших ограниченных целей, можно утверждать следующее.
В основу общей теории относительности положен, так называемый, «принцип эквивалентности», утверждающий, что масса инертная равна массе гравитационной. Другими словами, нет отдельно инертной массы и отдельно массы гравитационной, есть просто масса "ответственная" за все. Тот факт, что инертная и гравитационная массы строго пропорциональны друг другу было экспериментально установлено венгерским физиком Этвешем (серия экспериментов 1889–1908 годов) с относительной погрешностью не больше 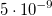 . После этого равенство инертной и гравитационной масс уже не проблема и обеспечивается соответствующим выбором единиц измерения. Результаты экспериментов Этвеша были использованы Эйнштейном при формулировании принципа эквивалентности.
. После этого равенство инертной и гравитационной масс уже не проблема и обеспечивается соответствующим выбором единиц измерения. Результаты экспериментов Этвеша были использованы Эйнштейном при формулировании принципа эквивалентности.
Необходимо признать и принять, что в рамках нерелятивистской ньютоновской механики внятно ответить на вопрос, что такое масса, невозможно. Для этого необходимы представления и средства и специальной и общей теорий относительности, но и их не вполне хватает, ввиду отсутствия на сегодняшний день законченной теории элементарных частиц. Это, впрочем, не привносит никаких трудностей в практическое использование ньютоновской механики.
В системе СИ единицей массы является килограмм (кг). Эта единица измерения является основной.
На рис. 3.8 показаны значения масс некоторых физических объектов.
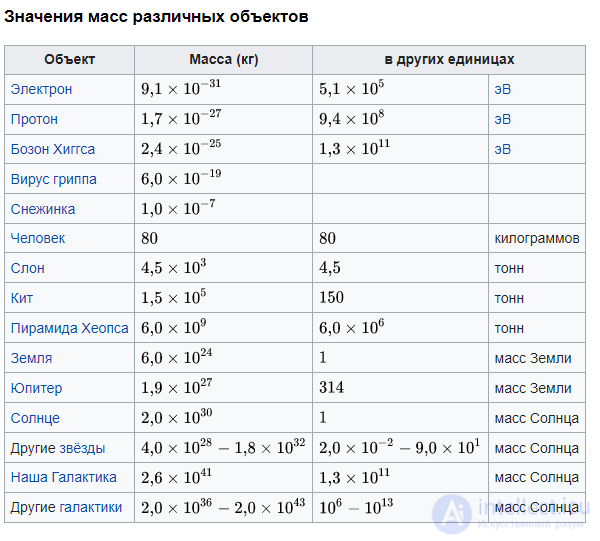
Рис. 3.8. Массы некоторых физических объектов
Отметим, что если определить энергию E как интеграл движения, сохранение которого у замкнутой системы обусловлено однородностью времени, а импульс 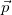 как интеграл движения, сохранение которого у замкнутой системы обусловлено однородностью пространства, то масса есть инвариантная величина, равная
как интеграл движения, сохранение которого у замкнутой системы обусловлено однородностью пространства, то масса есть инвариантная величина, равная
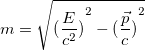
(3.2.8)
Здесь c — скорость света в вакууме, инвариантность которой экспериментально установлена в опытах Майкельсона, Майкельсона и Морли и многочисленных последователей: эксперименты повторялись в течение почти 50 лет (1881 по 1930 год) и, при многократно возраставшей (до 200 раз) точности, дали один и тот же результат. Инвариантность c есть основной постулат специальной теории относительности.
Как уже было сказано структура левой части второго закона Ньютона, записанного в виде (3.2.2) лишь подсказывает выражение для импульса. В действительности можно показать, что как в нерелятивистском так и в релятивистском случаях выражения для импульса (3.2.7) и (3.2.9) являются прямым следствием такого определения импульса:
Импульсом 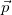 называется сохраняющаяся характеристика замкнутой системы, сохранение которой обусловлено однородностью пространства. Отсюда для одной нерелятивистской
называется сохраняющаяся характеристика замкнутой системы, сохранение которой обусловлено однородностью пространства. Отсюда для одной нерелятивистской 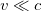 частицы следует, что ее импульс:
частицы следует, что ее импульс:
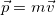
Отметим также, что уравнение движения, записанное в виде (3.2.6) с импульсом из (3.2.9) в отличие от (3.2.2) справедливо при любых скоростях.
Уравнение движения в форме (3.2.6)
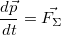
(3.2.10)
с импульсом 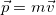 можно прочитать так:
можно прочитать так:
Скорость изменения импульса тела равна векторной сумме сил приложенных к телу.
Нередко весьма полезной оказывается и такая, следующая из (3.2.10), формулировка:
Приращение импульса тела за некоторое время  равно произведению средней суммарной силы, действующей на тело, на время ее действия:
равно произведению средней суммарной силы, действующей на тело, на время ее действия:
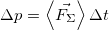
Второй закон Ньютона устанавливает единицу измерения силы 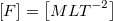 .
.
В системе СИ единицей силы является ньютон (H):
1 ед. силы СИ = 1 ед. массы СИ • 1 ед. ускорения СИ = 1 кг • 1 м/с2 = 1 H.>>
Дополнительная информация
http://www.plib.ru/library/book/17005.html – Стрелков C.П. Механика Изд. Наука 1971 г. – стр. 73–75: опыт с обрывом нитей, привязанных к массивному шару сверху и снизу;
Как уже отмечалось, сила не обязана быть постоянной: она может зависеть от времени, от положения тела в пространстве, от его скорости. Поэтому решение уравнения движения в общем случае — достаточно непростая задача. Приведем пример решения такой задачи.
Пример. На покоящееся в начале координат тело массой m в момент времени t = 0 начинает действовать периодическая сила
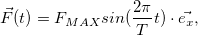
где 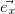 — орт оси 0х, а Т — период изменения силы. Половину периода сила направлена вдоль положительного направления оси 0х, следующую половину периода — в противоположную сторону. Найти зависимость от времени скорости частицы и ее положения (координаты) на оси 0х.
— орт оси 0х, а Т — период изменения силы. Половину периода сила направлена вдоль положительного направления оси 0х, следующую половину периода — в противоположную сторону. Найти зависимость от времени скорости частицы и ее положения (координаты) на оси 0х.
Поскольку максимальное значение силы равно 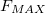 введем обозначение для максимального ускорения
введем обозначение для максимального ускорения
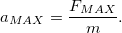
Тогда уравнение движения примет вид:
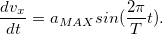
Отсюда скорость в момент времени t, с учетом того, что в начальный момент времени частица покоится 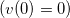 , равна
, равна
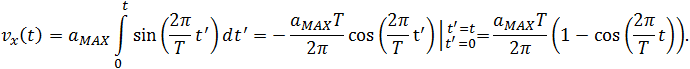
Положение тела на оси 0х также определяется интегрированием. Учитывая, что в начальный момент времени частица находится в начале координат (x(0) = 0), получаем
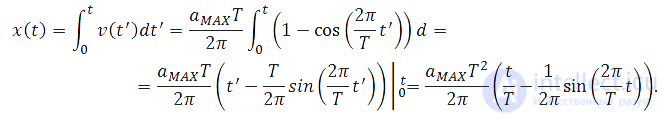
Графики зависимостей от времени ускорения (в единицах 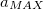 ), скорости (в единицах
), скорости (в единицах 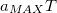 ) и координаты (в единицах
) и координаты (в единицах 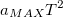 ) показаны на рис. 4.
) показаны на рис. 4.
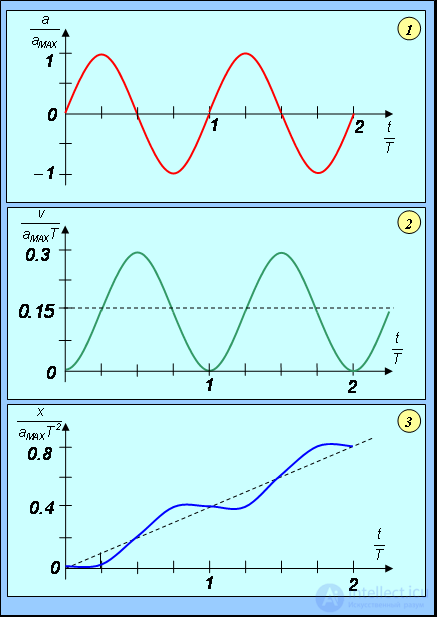
Рис. 3.9. Зависимость ускорения (1), скорости (2) и положения (3) частицы от времени
График ускорения, естественно, повторяет график силы. Скорость изменяется с тем же периодом, что и сила и ускорение, но, в отличие от силы и ускорения, нигде не меняет знака: скорость, набранная за время полупериода положительной силы 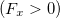 , снижается до нуля за время действия отрицательной
, снижается до нуля за время действия отрицательной 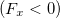 силы. Среднее за период значение координаты
силы. Среднее за период значение координаты 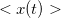 растет пропорционально времени. Сама координата осциллирует около этой линейной зависимости. Среднее за период значение скорости постоянно и равно
растет пропорционально времени. Сама координата осциллирует около этой линейной зависимости. Среднее за период значение скорости постоянно и равно
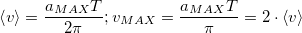
оно показано пунктиром на рис. 3.9. (2). Зависимость от времени средней координаты показана пунктиром на рис. 3.9. (3).
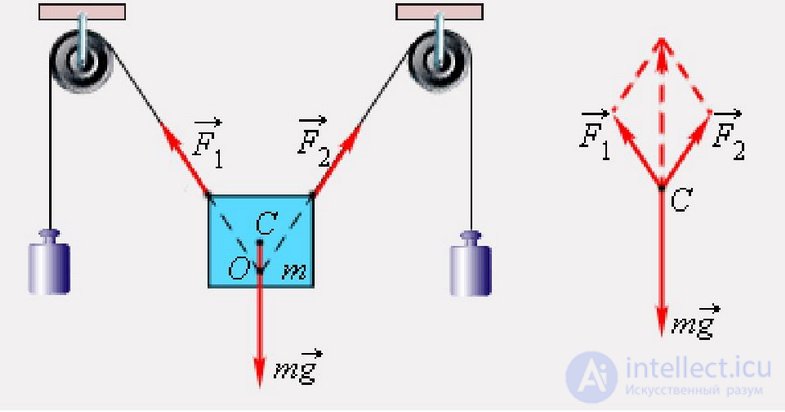
Как быть, если на нашу точку действует не одна сила, а несколько. В механике большое значение имеет принцип независимости действия сил:
Полное же ускорение тела равно сумме этих «частичных» ускорений. Согласно этому принципу, силы и ускорения можно разлагать на составляющие, использование которых приводит к существенному упрощению решения задач:
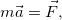
где
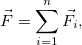
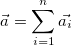
и
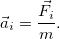
Сумму сил F называют равнодействующей (или результирующей) силой, приложенной к телу.
Третий закон Ньютона утверждает, что
Действие тел друг на друга всегда носит характер взаимодействия. Силы, с которыми взаимодействуют тела, равны по величине, противоположны по направлению и направлены вдоль одной общей прямой.
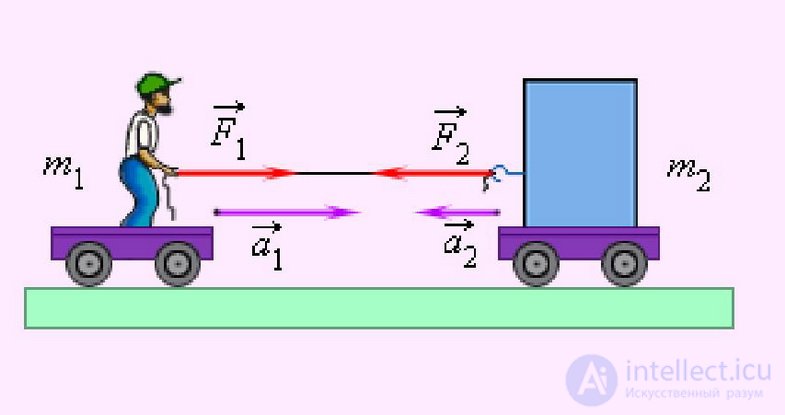
Рис. 3.11. Иллюстрация равенства сил 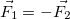
Если силу, действующую на первое тело в результате его взаимодействия со вторым телом обозначить 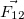 (первый индекс — номер того тела, на которое действует сила), а силу, действующую на второе тело в результате его взаимодействия с первым телом, соответственно
(первый индекс — номер того тела, на которое действует сила), а силу, действующую на второе тело в результате его взаимодействия с первым телом, соответственно 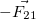 , то равенство сил по величине и их противоположность по направлению можно записать в виде
, то равенство сил по величине и их противоположность по направлению можно записать в виде
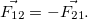
(3.2.11)
Или, что то же самое:
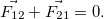
(3.2.12)
Две равные по величине и противоположно направленные силы образуют, как говорят, «пару сил». Об этом говорит сайт https://intellect.icu . Тот факт, что силы взаимодействия, согласно третьему закону Ньютона, направлены вдоль одной общей прямой можно сформулировать так: плечо a пары сил взаимодействия равно нулю. Сказанное поясняет нижеследующий рисунок. Согласно третьему закону Ньютона левая (на рисунке) ситуация а) имеет место, правая — в) невозможна.
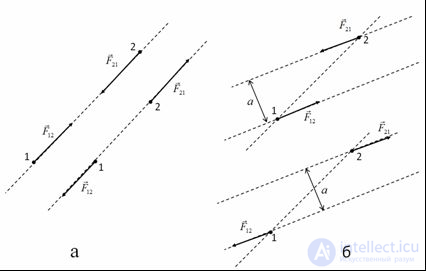
Рис. 3.12. Различные примеры приложения сил.
Отметим, что в простейшем случае двух покоящихся частиц, имеющих только скалярные характеристики, такие как масса, электрический заряд и тому подобное, третий закон Ньютона является вполне очевидным следствием однородности и изотропии пространства для замкнутой системы. В этом случае единственное физически выделенное направление в пространстве это направление единичного вектора  параллельного прямой, проходящей через те точки пространства, в которых покоятся частицы. Соответственно, силы взаимодействия могут быть направлены только по или против
параллельного прямой, проходящей через те точки пространства, в которых покоятся частицы. Соответственно, силы взаимодействия могут быть направлены только по или против  .
.
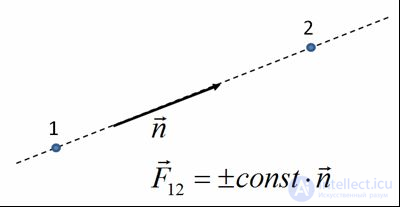
Рис.3.13. Направление силы взаимодействия двух материальных точек.
Однако закон равенства действия и противодействия выполняется лишь в предположении о бесконечной скорости распространения сигналов. Даже в простейшем случае электро-магнитного взаимодействия третий закон Ньютона соблюдается только в пределе 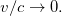 В качестве примера рассмотрим взаимодействие двух положительных зарядов Q1 и Q2 (Q1 > 0; Q2 > 0), движущихся соответственно со скоростями v1 и v2 , на каждой из которых со стороны другого заряда действуют силы F1 и F2 (Рис. 3.14)
В качестве примера рассмотрим взаимодействие двух положительных зарядов Q1 и Q2 (Q1 > 0; Q2 > 0), движущихся соответственно со скоростями v1 и v2 , на каждой из которых со стороны другого заряда действуют силы F1 и F2 (Рис. 3.14)
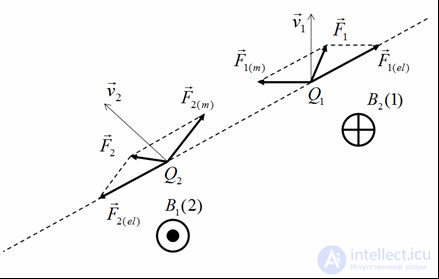
Рис.3.14. Электромагнитное взаимодействие движущихся зарядов (В этом случае третий закон Ньютона не выполняется, т.к. заряды не являются изолированной системоу. В этом взаимодействии участвуют также и поля E и H).
Каждую из этих сил F1 и F2 можно предоставить в виде двух составляющих. Первая составляющая есть сила электрического взаимодействия по закону Кулона. Она действует по линии, соединяющей заряды, F1(el) = –F2(el) и удовлетворяет требованиям третьего закона Ньютона. Но кроме электрического взаимодействия зарядов существует их магнитное взаимодействие: каждый из движущихся зарядов в точке нахождения другого заряда создает магнитное поле с индукцией B. Магнитное поле действует на заряд, движущийся со скоростью v, с силой Лоренца, направленной перпендикулярно скорости.
В ситуации, изображенной на рис. 3.14, поле B1, создаваемое зарядом Q1 в точке нахождения заряда Q2, направленного перпендикулярно плоскости рисунка к нам, а поле B2, создаваемое зарядом Q2 в точке нахождения заряда Q1, направленного перпендикулярно плоскости чертежа от нас. Магнитная сила Лоренца, перпендикулярна скорости v и магнитной индукции B. Силы Лоренца F1(m) и F2(m), действующие на каждый из зарядов Q1 и Q2, не совпадают по направлению и, следовательно, не могут удовлетворять закону действия и противодействия. Из рисунка очевидно, что результирующая сила действия первого заряда на второй («действие») НЕ равна результирующей силе второго заряда на первый («противодействие»), т. е. третий закон Ньютона не выполняется.
Заметим, что при 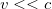 силы магнитного происхождения много меньше электрических. Поскольку отклонение от закона равенства действия и противодействия обусловлено магнитными силами, то это отношение при не очень больших скоростях несущественно и им обычно можно пренебречь.
силы магнитного происхождения много меньше электрических. Поскольку отклонение от закона равенства действия и противодействия обусловлено магнитными силами, то это отношение при не очень больших скоростях несущественно и им обычно можно пренебречь.
В этом разделе мы приведем примеры сил, действующих в механических системах. Это сила тяжести и вес тела, силы упругости и трения. Происхождение силы тяжести связано с одним из фундаментальных взаимодействий — гравитационным. (С этим взаимодействием мы познакомимся подробнее при изучении закона всемирного тяготения.) Другое фундаментальное взаимодействие — электромагнитное, то есть взаимодействие между электрическими зарядами и токами, лежит в основе сил, связанных с деформацией тел. Это, прежде всего силы упругости, а также силы трения, возникающие за счет деформации при соприкосновении шероховатых поверхностей. При деформации нарушается равновесное распределение зарядов внутри атомов, молекул или ионов, из которых состоят тела, что приводит к изменению действующих между ними сил.
Сила тяжести и вес. Еще Галилей понял, что если не учитывать силу сопротивления воздуха, действующую на движущееся в нем тело, то все тела будут падать на Землю с одним и тем же ускорением 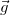 . Силу, «обеспечивающую» это ускорение, принято называть силой тяжести.
. Силу, «обеспечивающую» это ускорение, принято называть силой тяжести.
В системе отсчета, связанной с Землей, на всякое тело массой m действует сила тяжести
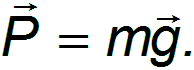
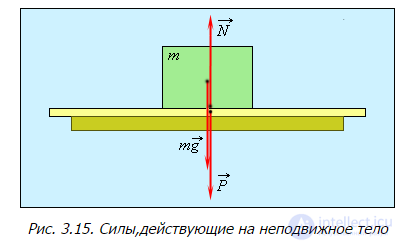
Рис. 3.15. Силы,действующие на неподвижное тело
Сила, с которой тело действует на подвес или опору, называется весом тела.
Когда тело покоится, то сила тяжести уравновешивается реакцией опоры или подвеса 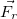 , то есть
, то есть
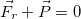
По третьему закону Ньютона вес тела 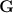 равен
равен

Если же тело вместе с опорой или подвесом движется с ускорением, то вес тела не равен силе тяжести.

Рис. 3.16. Силы,действующие на тело, двужущееся ускоренно
Попутно напомним, что, по определению, вертикальным (вниз) направлением называется направление вектора свободного падения 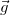 . Соответственно, любое направление перпендикулярное
. Соответственно, любое направление перпендикулярное 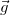 является горизонтальным.
является горизонтальным.
Пусть подвес в виде укрепленной на раме пружины движется вместе с лифтом с ускорением а (рис. 3.17).

Рис. 3.17. Зависимость веса движущегося тела от ускорения опоры
Тогда уравнение движения тела будет иметь вид
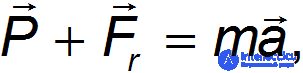
где 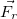 — реакция подвеса, то есть сила, с которой пружина действует на тело. По третьему закону Ньютона тело действует на пружину с силой, равной —
— реакция подвеса, то есть сила, с которой пружина действует на тело. По третьему закону Ньютона тело действует на пружину с силой, равной — 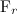 , которая по определению представляет собой вес тела
, которая по определению представляет собой вес тела 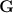 . Заменив в уравнении движения реакцию опоры
. Заменив в уравнении движения реакцию опоры 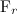 силой —
силой — 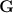 , а силу тяжести
, а силу тяжести 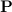 — произведением mg, получим:
— произведением mg, получим:
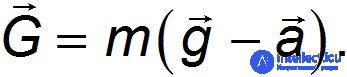
Спроецируем полученное соотношение на вертикальную ось у,направленную вертикально вниз:
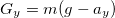
Отсюда вытекает, что по модулю вес  может быть как больше, так и меньше, чем сила тяжести
может быть как больше, так и меньше, чем сила тяжести 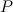 (см. рис. 6). При свободном падении рамы с подвесом
(см. рис. 6). При свободном падении рамы с подвесом
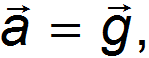
и сила 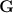 , с которой тело действует на подвес, равна нулю: наступает состояние невесомости. «Исчезновение» веса тела, то есть силы давления на опору, не означает исчезновения инерционных свойств тела (его массы).
, с которой тело действует на подвес, равна нулю: наступает состояние невесомости. «Исчезновение» веса тела, то есть силы давления на опору, не означает исчезновения инерционных свойств тела (его массы).
В фантастической повести А.Р. Беляева «Звезда КЭЦ» описывается первое пребывание героя в состоянии невесомости. Он оттолкнулся и летит вдоль коридора космической станции:
« — Хватайтесь за ремешок! — крикнул Крамер. Эти ремешки, вроде ручек портпледа, были всюду: на стенах, на полу, на потолке. Я ухватился за ручку, ожидая, что меня рванет при остановке, но в тот же миг с удивлением почувствовал, что в руке не ощущается напряжения».
Сила упругости. При деформации тела возникают силы упругости, препятствующие этой деформации. При небольших деформациях возникающие силы пропорциональны величине деформации. Если пружина в нормальном (ненагруженном) состоянии имеет длину 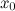 и мы деформируем ее (растягиваем или сжимаем) ее до длины
и мы деформируем ее (растягиваем или сжимаем) ее до длины  , то на нашу руку действует сила упругости
, то на нашу руку действует сила упругости

Коэффициент 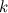 называется коэффициентом жесткости пружины, знак «минус» указывает, что сила упругости препятствует деформации пружины. Приведенное уравнение описывает простейший случай закона Гука.
называется коэффициентом жесткости пружины, знак «минус» указывает, что сила упругости препятствует деформации пружины. Приведенное уравнение описывает простейший случай закона Гука.
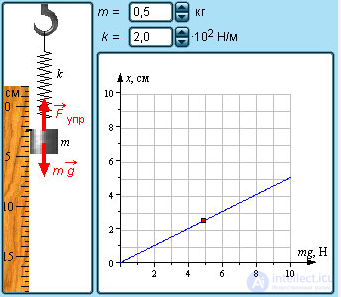
Линейные упругие деформации и закон Гука.
Возникновение упругой силы в процессе колебаний тела на пружине показано на рис. 3.18.
Пример. Каков эффективный коэффициент жесткости 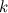 для пружины, составленной из двух других пружин с коэффициентами жесткости
для пружины, составленной из двух других пружин с коэффициентами жесткости 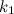 и
и 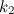 , если пружины соединены: а) последовательно (рис. 3.19), б) параллельно (рис. 3.20).
, если пружины соединены: а) последовательно (рис. 3.19), б) параллельно (рис. 3.20).
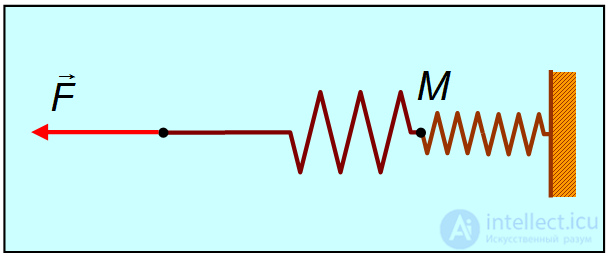
Рис. 3.19. Последовательное соединение пружин
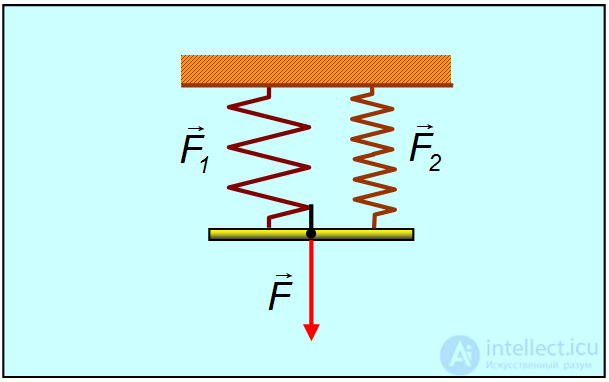
Рис. 3.20. Параллельное соединение пружин
Решение. Если растягивать последовательно соединенные пружины, то возникающие в каждой из них упругие силы одинаковы и равны растягивающей силе 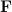 (см. рис. 7): точка соединения
(см. рис. 7): точка соединения 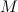 находится в равновесии. Следовательно, удлинения пружин равны соответственно
находится в равновесии. Следовательно, удлинения пружин равны соответственно
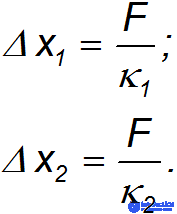
Полное удлинение составной пружины равно

Эффективная жесткость последовательно соединенных пружин определяется из соотношения:
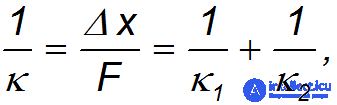
откуда
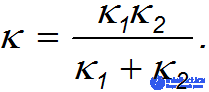
При растягивании параллельно соединенных пружин одинаковы их удлинения  , так что в каждой из них возникает своя упругая сила:
, так что в каждой из них возникает своя упругая сила:
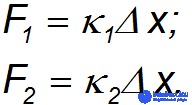
В состоянии покоя сумма этих сил равна растягивающей силе (см. рис. 3.20):
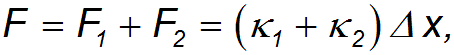
так что коэффициент жесткости параллельно соединенных пружин равен
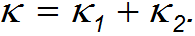
В ряде задач, когда коэффициент жесткости велик, пренебрегают величиной деформации, но не ее последствиями возникающими силами упругости. Это тоже пример физической абстракции, модели.
Трение, которое может существовать между телами, не движущимися друг относительно друга, называется трением покоя.
Имеет место следующее утверждение относительно силы трения покоя:
Сила трения покоя всегда равна по величине и противоположна по направлению внешней силе, которая в отсутствие трения должна была бы вызвать относительное скольжение тел.
Однако сила трения покоя не может превосходить некоторой максимальной величины 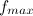 . Пока внешняя сила меньше
. Пока внешняя сила меньше 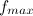 , относительное скольжение тел не возникает, так как сила трения покоя «автоматически» принимает значение, компенсирующее действие внешней силы.
, относительное скольжение тел не возникает, так как сила трения покоя «автоматически» принимает значение, компенсирующее действие внешней силы.
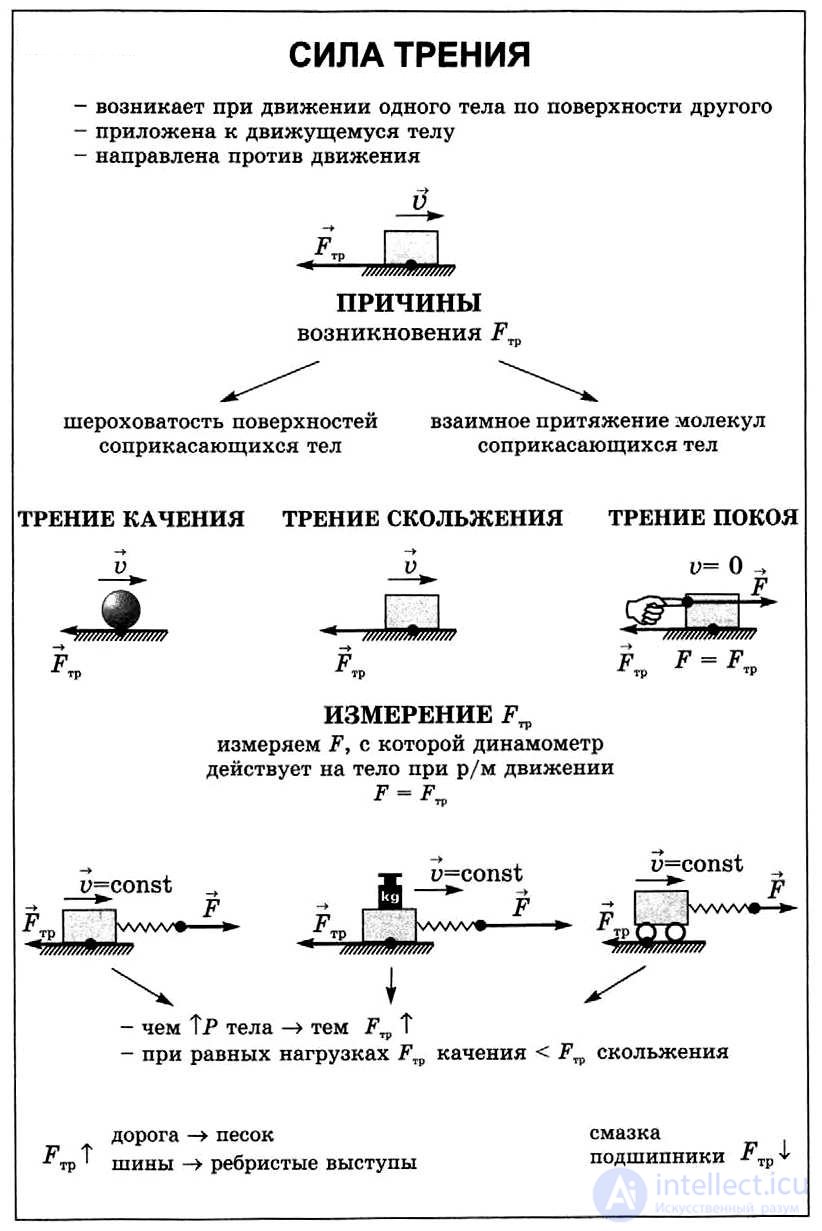
Сила трения покоя и сила трения скольжения
Силы сухого трения между объектами, движущимися друг относительно друга, называются силами трения скольжения.
Они довольно сложным образом зависят от скорости относительного движения, но для широкого класса явлений и соприкасающихся пар материалов их можно считать постоянными и равными максимальному значению силы трения покоя. Они направлены так, чтобы препятствовать относительному проскальзыванию соприкасающихся тел.
Для максимального значения силы трения покоя экспериментально установлено соотношение — закон Амонтона-Кулона:
Максимальная сила трения покоя пропорциональна силе нормального давления, прижимающего соприкасающиеся тела
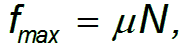
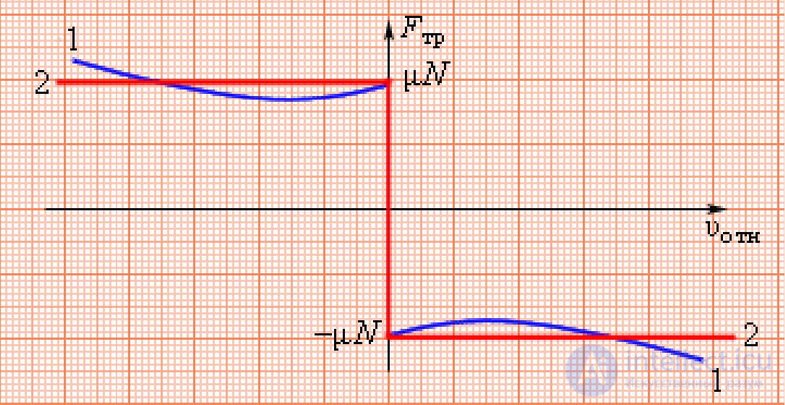
Рис. 3.21. Зависимость силы трения от относительной скорости тел
где 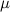 — коэффициент трения покоя, зависящий от свойств соприкасающихся поверхностей. Характерные значения
— коэффициент трения покоя, зависящий от свойств соприкасающихся поверхностей. Характерные значения 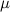 приведены в таблице.
приведены в таблице.
Таблица
Коэффициент трения покоя для некоторых пар соприкасающихся материалов

Следует иметь в виду, что коэффициент трения покоя сильно зависит не только от материалов соприкасающихся тел, но и от состояния (обработки) их поверхностей,а также от присутствия посторонних веществ, например, ржавчины на поверхности стальных деталей.
При контакте твердых тел между ними действуют не только силы сухого трения (покоя или скольжения). Из-за деформации тел могут возникать также силы трения качения. Они гораздо меньше сил трения покоя, и ими обычно пренебрегают.
Следующий пример демонстрирует случай, когда сила реакции опоры не параллельна силе тяжести. Пусть тело массой 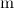 скользит по наклонной плоскости, которая составляет угол
скользит по наклонной плоскости, которая составляет угол 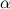 с горизонтом (рис. 3.22).
с горизонтом (рис. 3.22).
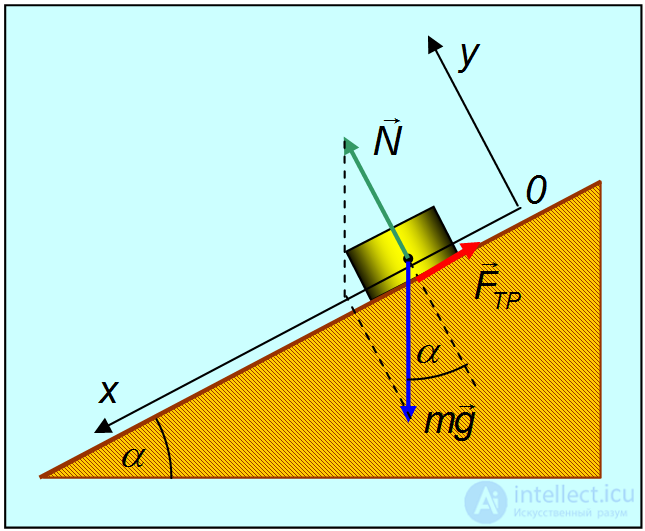
Рис. 3.22. Движение тела по наклонной плоскости
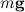 ) и воздействие со стороны плоскости (оно характеризуется силой реакции опоры
) и воздействие со стороны плоскости (оно характеризуется силой реакции опоры  , где
, где 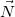 — нормальная составляющая силы реакции (сила нормального давления), а
— нормальная составляющая силы реакции (сила нормального давления), а 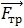 — тангенциальная составляющая силы реакции, то есть сила трения). Соответственно, уравнение второго закона Ньютона или уравнение движения имеет вид:
— тангенциальная составляющая силы реакции, то есть сила трения). Соответственно, уравнение второго закона Ньютона или уравнение движения имеет вид:
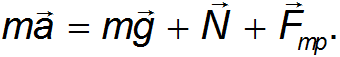
Чтобы найти ускорение тела, необходимо перейти от векторов к их проекциям на соответствующим образом выбранные направления. (Обычно целесообразно в качестве одной из координатных осей выбрать ось вдоль направления движения). Спроецируем векторы, входящие в уравнение, на направления 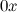 и
и 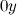 (см. рис. 3.22):
(см. рис. 3.22):
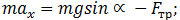
(3.2.13)
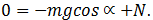
Предполагая, что тело скользит вниз, вместо 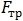 подставим в первое уравнение силу трения скольжения
подставим в первое уравнение силу трения скольжения
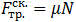
со значением N, следующим из второго уравнения, то есть:

(3.2.15)
Тогда из первого уравнения, после деления его на массу, для ускорения с которым тело скользит вниз, получаем:
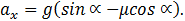
Решим задачу в такой постановке: тело положили на наклонную плоскость и без толчка отпустили, то есть начальная скорость тела равна нулю. Если потребуется определение зависимости координаты x тела от времени t, можно положить, что ее начальное значение также равным нулю.
Строго говоря, заранее неизвестно начнет тело скользить вниз или нет. Предположим, что тело остается в покое, найдем из уравнений движения значение силы трения покоя и получим условие сохранения состояния покоя из требования, что сила трения покоя не может превышать свое максимальное значение равное силе трения скольжения. Это общий прием, который приводит к результату — неравенству, при выполнении которого, сохраняется состояние покоя — не только в данном простейшем случае, но и в значительно более сложных ситуациях.
Если тело покоится, то
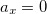
(3.2.16)
и фигурирующая в (3.2.13) сила трения есть сила трения покоя
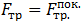
(3.2.17)
Подставляя (3.2.16) и (3.2.17) в (3.2.13) для силы трения покоя получаем
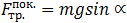
(3.2.18)
Но, сила трения покоя не может превышать свое максимальное значение, равное силе трения скольжения. Потребовав, чтобы (3.2.18) не превышало (3.2.15), после сокращений получаем условие сохранения состояния покоя
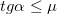
(3.2.19)
При выполнении противоположного неравенства (большой угол, малый коэффициент трения)
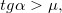
тело будет, замедляясь скользить вверх, остановится и, «не удержавшись», заскользит вниз.
Сухое трение возникает при соприкосновении прижатых друг к другу тел в результате их относительного перемещения. Поверхности реальных тел не являются гладкими, на них имеются шероховатости (рис. 3.23). Поэтому касание тел происходит не по всей площади видимого соприкосновения, а в отдельных областях, расположенных на выступах поверхностей. При скольжении области соприкосновения разрушаются и возникают вновь. Важными последствиями трения скольжения на практике являются нагревание и износ трущихся поверхностей.

Рис. 3.23. Механизм возникновения сухого трения
Сила сопротивления среды. При движении тела в жидкой или газообразной среде на него действует сила сопротивления среды, зависящая от скорости тела. При малых скоростях движения сила сопротивления пропорциональна скорости
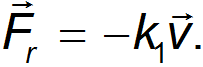
При увеличении скорости тела сила сопротивления зависит от скорости по квадратичному закону
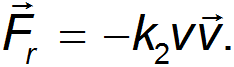
В обоих случаях сила сопротивления направлена против вектора скорости тела.
Зависимость силы от скорости тела приводит к существованию установившейся скорости движения, когда сила сопротивления достигает величины движущей силы.
Пример. Рассмотрим медленное движение тела под действием постоянной силы 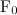 = const в жидкой среде. В проекциях на направление силы второй закон Ньютона для тела имеет вид
= const в жидкой среде. В проекциях на направление силы второй закон Ньютона для тела имеет вид
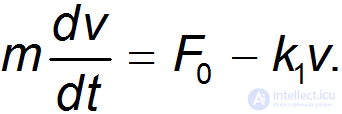
Пусть тело начинает двигаться без начальной скорости
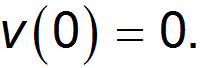
Интегрируя уравнение второго закона Ньютона, получим
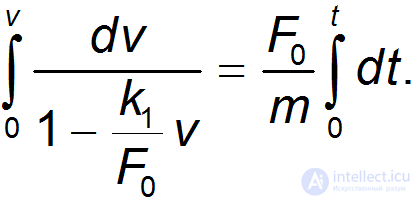
или
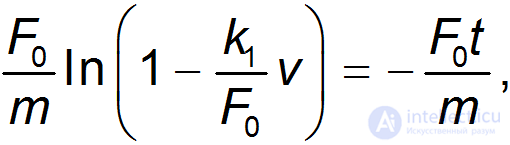
откуда зависимость скорости тела от времени принимает вид:
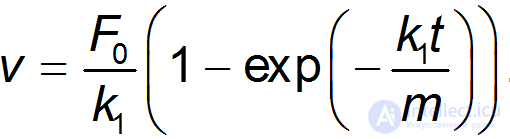
На рис. 3.24 представлена графически зависимость скорости тела от времени.
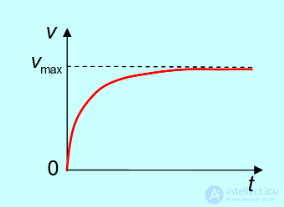
Рис. 3.24. Скорость движения тела в вязкой среде
Видно, что скорость тела с течением времени стремится к предельному значению

Рассмотрим систему 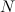 материальных точек
материальных точек  ,
, 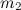 , …,
, …, 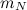 , положения которых задаются радиус-векторами
, положения которых задаются радиус-векторами 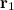 ,
, 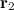 , …,
, …, 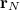 , а их импульсы равны
, а их импульсы равны 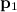 ,
, 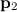 ,...,
,..., 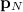 , соответственно (рис. 3.25).
, соответственно (рис. 3.25).
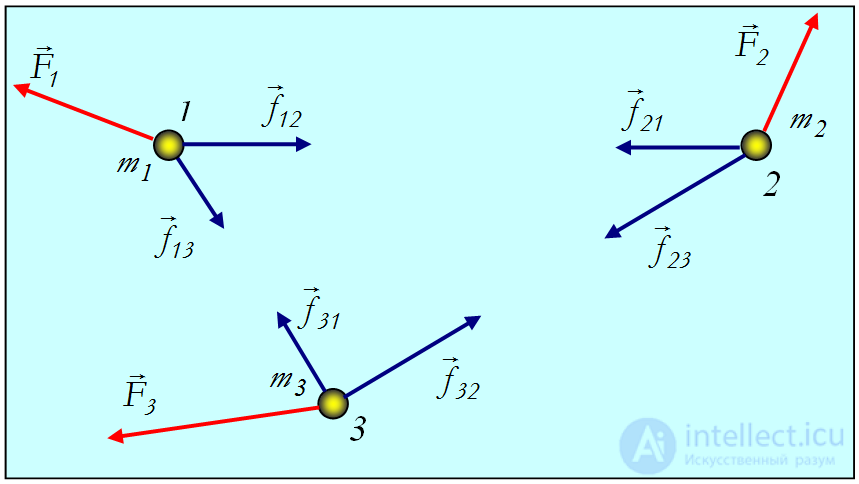
Рис. 3.25. Система взаимодействующих частиц
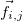 , где индексы показывают, что данная сила действует на тело с номером
, где индексы показывают, что данная сила действует на тело с номером 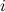 со стороны тела с номером
со стороны тела с номером 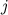 . Кроме того, на тело с номером действует какая-то внешняя сила
. Кроме того, на тело с номером действует какая-то внешняя сила 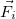 .
.
Напишем уравнение второго закона Ньютона (скорость изменения импульса тела равна сумме всех действующих на тело сил) для всех 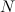 материальных точек системы
материальных точек системы
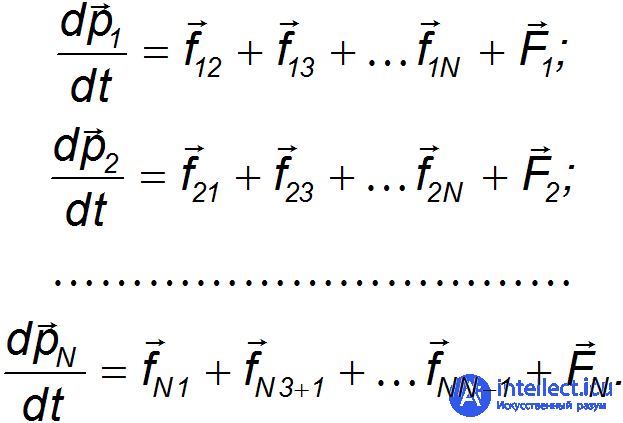
Сложим вместе эти 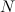 уравнений. Сумма всех внутренних сил в правой части получится равной нулю. Действительно, она состоит из парных слагаемых типа
уравнений. Сумма всех внутренних сил в правой части получится равной нулю. Действительно, она состоит из парных слагаемых типа
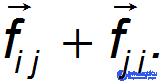
По третьему закону Ньютона силы взаимодействия двух материальных точек 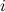 и
и 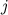 равны по величине и противоположно направлены (действуют вдоль прямой, соединяющей эти материальные точки):
равны по величине и противоположно направлены (действуют вдоль прямой, соединяющей эти материальные точки):

Поэтому в правой части у нас останется только сумма всех внешних сил:
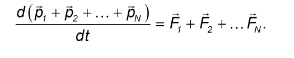
Сумма
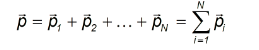
импульсов частиц, образующих механическую систему, называется импульсом системы.
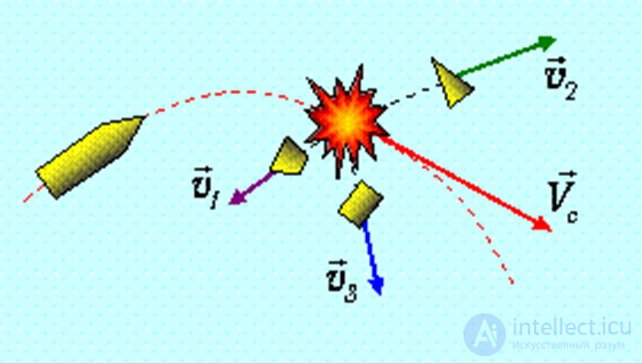
Рис. 3.26. Суммарный импульс осколков снаряда равен импульсу самого снаряда до взрыва.
Импульс системы удовлетворяет уравнению
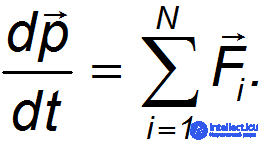
Система тел, взаимодействующих только между собой и не взаимодействующих с другими телами, называется замкнутой.
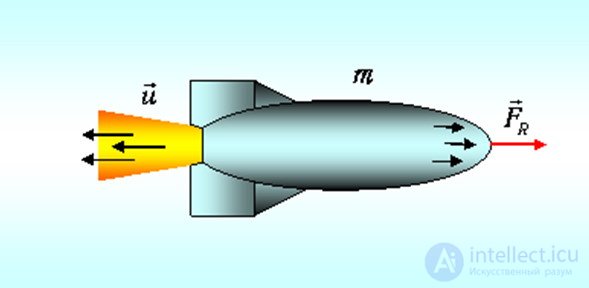
Рис. 3.27. Суммарный импульс снаряда и вылетающих частиц не меняется со временем
Иными словами, на замкнутую систему не действуют внешние силы. При отсутствии внешних сил
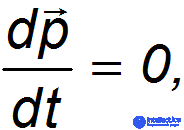

Суммарный импульс
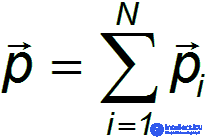
замкнутой системы постоянен сохраняется, то есть постоянен во времени.
Возможны ситуации, когда внешние силы не равны нулю, но равна нулю проекция их равнодействующей на некоторое направление  . Тогда, как следует из (3.4.1), переписанного в виде
. Тогда, как следует из (3.4.1), переписанного в виде
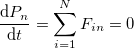
будет сохраняться проекция импульса системы 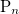 на это же направление. Примером может служить уже рассмотренное движение тела, брошенного под углом к горизонту. На тело действует сила тяжести, направленная вертикально вниз. Ее проекция на горизонтальную ось равна нулю, и потому горизонтальная проекция импульса сохраняется, соответственно,постоянна горизонтальная проекция скорости.
на это же направление. Примером может служить уже рассмотренное движение тела, брошенного под углом к горизонту. На тело действует сила тяжести, направленная вертикально вниз. Ее проекция на горизонтальную ось равна нулю, и потому горизонтальная проекция импульса сохраняется, соответственно,постоянна горизонтальная проекция скорости.
Применение закона сохранения импульса позволяет решить многие задачи, например, когда неизвестны точные силы, действующие в системе.
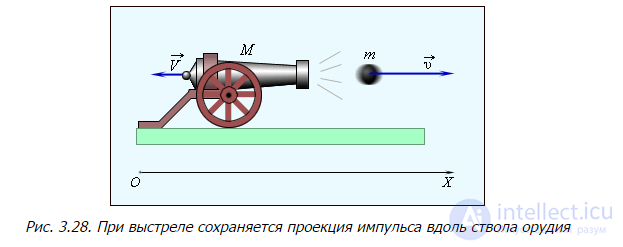
Рис. 3.28. При выстреле сохраняется проекция импульса вдоль ствола орудия
Пример. Стреляя из автомата АК-47, солдат испытывает отдачу: на него действует средняя сила Fcp, эквивалентная весу массы M = 6.5 кг. Учитывая, что масса пули m = 7 г и вылетает она с начальной скоростью 850 м/с, определить скорострельность n автомата (то есть количество пуль, выпускаемых автоматом в единицу времени).
За время 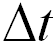 выпускается
выпускается 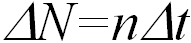 пуль. Они уносят импульс
пуль. Они уносят импульс 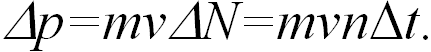 По закону сохранения такой же импульс передается автомату. Поэтому по второму закону Ньютона средняя сила отдачи равна
По закону сохранения такой же импульс передается автомату. Поэтому по второму закону Ньютона средняя сила отдачи равна
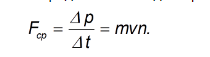
По условию 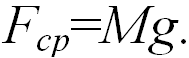 Отсюда находим скорострельность оружия:
Отсюда находим скорострельность оружия:
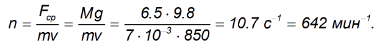
Естественно, при стрельбе очередями и, тем более, одиночными выстрелами число выстрелов в минуту будет меньшим.
Снова рассмотрим ту же систему материальных точек. Построим радиус-вектор  по следующему правилу:
по следующему правилу:
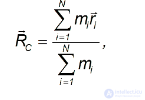
где 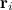 — радиус-вектор
— радиус-вектор 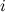 — той материальной точки системы, а
— той материальной точки системы, а 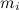 — ее масса.
— ее масса.
Радиус-вектор  определяет положение в пространстве центра инерции (центра масс) системы.
определяет положение в пространстве центра инерции (центра масс) системы.
Вовсе не обязательно, что в центре масс системы окажется какая-то материальная точка.
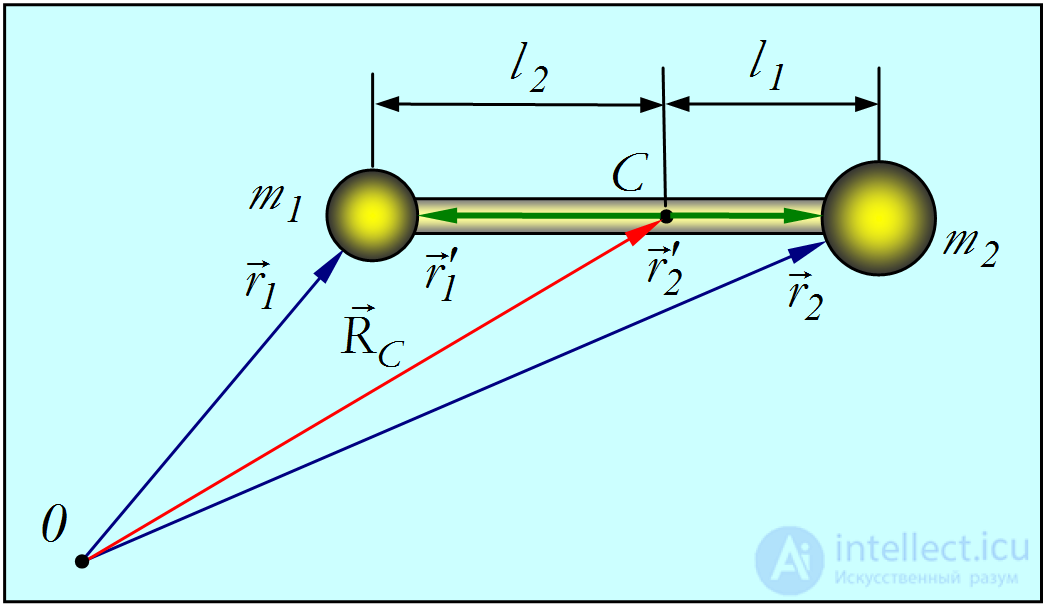
Рис. 3.29. Центр масс гантели
Из рис. видно, что
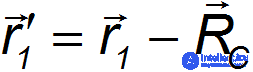
и
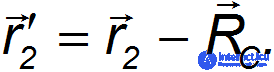
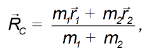
получим
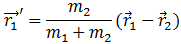
и
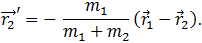
Отсюда следует, что центр масс лежит на прямой, проходящей через центры шаров. Расстояния l1 и l2 между шарами и центром масс равны соответственно
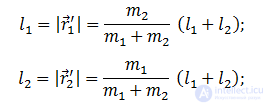
Центр масс ближе к тому шарику, масса которого больше, что видно из отношения:
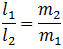
Определим, с какой скоростью движется центр инерции системы. Дифференцируем по времени обе части:
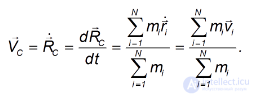
В числителе полученного выражения в правой части стоит сумма импульсов всех точек, то есть импульс 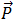 системы. В знаменателе стоит полная масса системы
системы. В знаменателе стоит полная масса системы
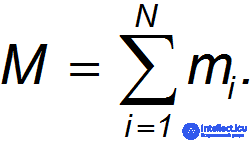
Мы получили, что скорость центра инерции связана с импульсом системы и ее полной массой таким же соотношением, какое справедливо для материальной точки:
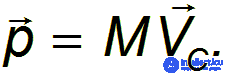
Таким образом, можно считать, что скорость VC является скоростью системы как целого. Она, разумеется, может отличаться от скоростей каждого из тел, входящих в систему.
Центр масс замкнутой системы движется всегда с постоянной скоростью, поскольку импульс такой системы сохраняется.
Если продифференцировать теперь выражение для импульса системы по времени и учесть, что производная импульса системы есть равнодействующая внешних сил, то получим уравнение движения центра масс системы в общем случае:

Видно, что
Центр масс системы движется точно так же, как двигалась бы материальная точка с массой, равной массе всех частиц системы, под действием векторной суммы всех внешних сил, приложенных к системе.
Если имеется система материальных точек, внутреннее расположение и движение которых нас не интересует, мы вправе считать ее материальной точкой с координатами радиус-вектора центра инерции и массой, равной сумме масс материальных точек системы.
Если связать с центром масс замкнутой системы материальных точек (частиц) систему отсчета (ее называют системой центра масс), то полный импульс всех частиц в такой системе окажется равным нулю. Таким образом, в системе центра масс замкнутая система частиц как целое покоится, и существует только движение частиц относительно центра масс. Поэтому ясно выявляются свойства внутренних процессов, протекающих в замкнутой системе.
 в нашем теле небольшим объемом
в нашем теле небольшим объемом 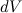 . Масса, заключенная в этом объеме, равна
. Масса, заключенная в этом объеме, равна 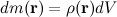 , где
, где 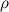 — плотность вещества тела, которая может и не быть постоянной по его объему. Сумма по всем таким элементарным массам заменяется теперь на интеграл по всему объему
— плотность вещества тела, которая может и не быть постоянной по его объему. Сумма по всем таким элементарным массам заменяется теперь на интеграл по всему объему 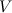 тела, так что для положения центра масс тела получается выражение
тела, так что для положения центра масс тела получается выражение
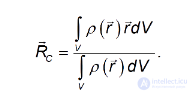
Если вещество тела однородно, плотность его постоянна, и ее можно вынести из-под знака интеграла, так что она сократится в числителе и знаменателе. Тогда выражение для радиус-вектора центра масс тела принимает вид
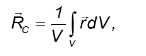
где 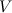 — объем тела.
— объем тела.
И в случае непрерывного распределения масс справедливо утверждение, что
Центр масс твердого тела движется так, как двигалась бы материальная точка с массой, равной массе тела, под действием векторной суммы всех внешних сил,приложенных к телу.
Пример. Если снаряд взрывается в некоторой точке своей параболической траектории, то осколки летят по самым различным траекториям, но его центр масс продолжает движение по параболе.
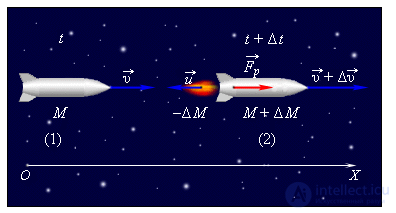
Рассмотрим движение тела, масса которого меняется в процессе движения, на примере движения ракеты.
Принцип движения ракеты заключается в том, что продукты сгорания топлива с большой скоростью выбрасываются из ракеты, толкая ее при этом в противоположную сторону.
Заметим, что при движении ракеты ее масса непрерывно изменяется, следовательно, второй закон Ньютона в рассмотренной ранее форме для описания движения ракеты неприменим.
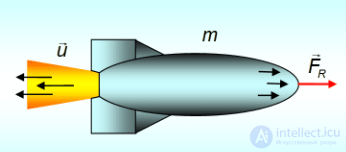
Рис. 3.30. Принцип движения ракеты
Пусть 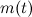 — масса ракеты в момент
— масса ракеты в момент 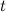 , а
, а 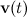 — ее скорость. Импульс ракеты будет
— ее скорость. Импульс ракеты будет
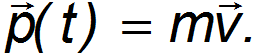

За время 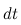 масса ракеты и ее скорость получают приращения
масса ракеты и ее скорость получают приращения 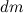 (причем
(причем 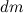 < 0), так как масса ракеты убывает) и
< 0), так как масса ракеты убывает) и 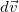 соответственно, так что к моменту времени
соответственно, так что к моменту времени 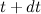 они будут равны
они будут равны
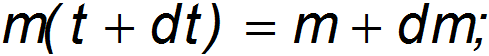
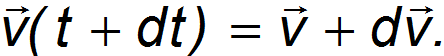
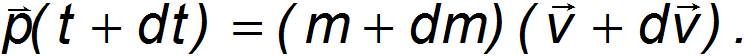
Кроме этого следует учесть импульс выброшенных за время 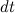 газов:
газов:
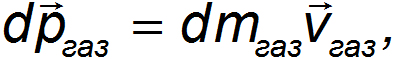
где 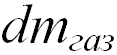 — масса выброшенных за время
— масса выброшенных за время 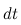 газов,
газов, 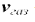 — их скорость относительно Земли.
— их скорость относительно Земли.
Воспользуемся вторым законом Ньютона в импульсной форме. Тогда
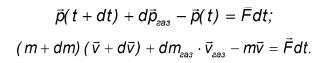
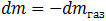 (масса ракеты уменьшилась на массу выброшенных из сопла двигателя газов):
(масса ракеты уменьшилась на массу выброшенных из сопла двигателя газов):
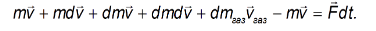
Введем u — скорость истечения газовой струи относительно ракеты. Тогда

После преобразований и удержания членов первого порядка малости (член второго порядка малости 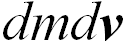 отброшен) получаем
отброшен) получаем
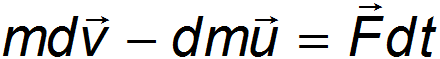
или
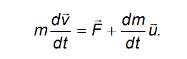
Данное уравнение по форме напоминает второй закон Ньютона, однако здесь возникает дополнительное слагаемое
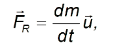
называемое реактивной силой. C учетом этого уравнение движения принимает вид
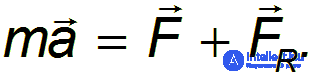
Это уравнение движения тела переменной массы носит название уравнения Мещерского.
Величина
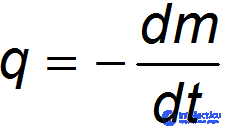
называется расходом топлива.
Рассмотрим движение ракеты в отсутствие внешних сил (F = 0) (рис. 3.31). Спроецируем уравнение Мещерского на направление движения ракеты  :
:
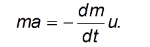

Рис 3.31. Движение ракеты в отсутствие внешних сил
С учетом, что

получаем
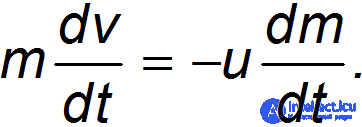
Разделим переменные:
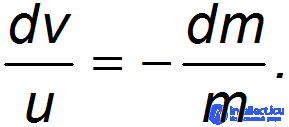
Обычно можно считать, что скорость истечения газов относительно ракеты постоянна. Интегрируя полученное уравнение, находим
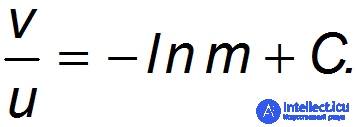
Пусть в начальный момент 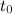 = 0 мы имеем
= 0 мы имеем
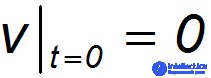
и
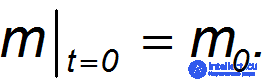
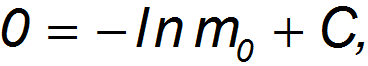
откуда находим постоянную интегрирования

Тогда формула для скорости ракеты, называемая формулой Циолковского, принимает вид
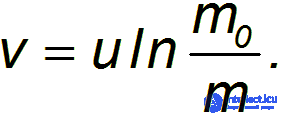
Ясно, что конечная скорость ракеты определяется скоростью истечения газовой струи, которая — в случае химического двигателя с реакцией окисления и выбросом продуктов реакции — зависит от температуры сгорания T и молярной массы газов M
 .
.
Следовательно, наиболее эффективным топливом будет водород с очень высокой температурой сгорания и малой молярной массой. Водород как топливо нашел широкое применение в космонавтике, несмотря на повышенную пожароопасность и потребность (при хранении в баках ракеты) в очень низких (криогенных) температурах.
Пример. Пусть ракете необходимо сообщить первую космическую скорость  = 8 км/с. Если использовать топливо со скоростью истечения
= 8 км/с. Если использовать топливо со скоростью истечения  = 1 км/с (порох), то отношение массы полезной нагрузки к стартовой массе ракеты будет
= 1 км/с (порох), то отношение массы полезной нагрузки к стартовой массе ракеты будет

Если же использовать топливо с  = 2 км/с (водород), то
= 2 км/с (водород), то
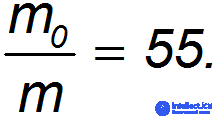
Видно, что при одинаковой полезной нагрузке стартовая масса ракеты во втором случае будет почти в 50 раз меньше, чем в первом.
ученые И.В. Мещерский и К. Э. Циолковский. Вклад этих ученых в развитие реактивного движения

Во время Великой Отечественной войны важную роль в боевых действиях нашей армии сыграли реактивные установки («катюши») – многозарядные пусковые установки, размещаемые на грузовых автомашинах.

Современные боевые ракеты имеют как обычные , так и ядерные заряды. Они способны за несколько десятков минут преодолеть несколько тысяч километров. В зависимости от места старта и нахождения цели их делят на классы: «земля-земля», «земля-воздух», «воздух-земля».

Создание фотонной ракеты позволит путешествовать к звездам и галактикам.

Зададим себе вопрос: почему мы, следуя Ньютону, сформулировали принцип инерции Галилея в виде отдельного (первого) закона движения? Ведь он следует из второго закона при равенстве нулю всех действующих на тело сил. Действительно, это так. Но по отношению к какой системе отсчета мы формулируем законы динамики?
Среди всех мыслимых систем отсчета эти законы наиболее просто выглядят в так называемых инициальных системах отсчета. Рассмотрим тело, находящееся настолько далеко от других тел, что оно не испытывает никаких воздействий со стороны последних. Такое тело назовем свободно движущимся. Если теперь с таким телом связать систему отсчета, то в ней свободное движение другого тела выглядит наиболее просто: оно будет равномерным и прямолинейным. Это и есть закон инерции, открытый Галилеем. Смысл закона заключается именно в том, что
Существует такая система отсчета, в которой свободная материальная точка находится в покое или движется равномерно и прямолинейно.
Система отсчета, в которой выполняется первый закон Ньютона, называется инерциальной.
Именно для инерциальной системы отсчета мы сформулировали второй закон Ньютона.
Инерциальная система отсчета — тоже определенная абстракция, используемая в науке. На практике свободно движущееся тело, равно как и инерциальная система отсчета, могут существовать лишь с большей или меньшей точностью. В огромном большинстве случаев нашу планету можно выбирать в качестве инерциальной системы отсчета (геоцентрическая система). В других случаях, например, для описания движения планет, в качестве таковой выбирается система, связанная с Солнцем (гелиоцентрическая система). Иногда и этого недостаточно, и тогда пользуются системой, связанной со звездами.
Итак, первый закон Ньютона постулирует, что существует такая система отсчета, в которой свободная материальная точка находится в покое, или движется равномерно и прямолинейно. Но если существует хотя бы одна инерциальная система, то любая другая система отсчета, движущаяся относительно нее равномерно и прямолинейно, также будет инерциальной.
Действительно, установим связь в описании движения той же материальной точки, рассматриваемой относительно двух разных систем отсчета.
Пусть дана система отсчета с началом координат в точке 0 и пусть дана другая система отсчета с началом координат в точке 0' (рис. 3.31).
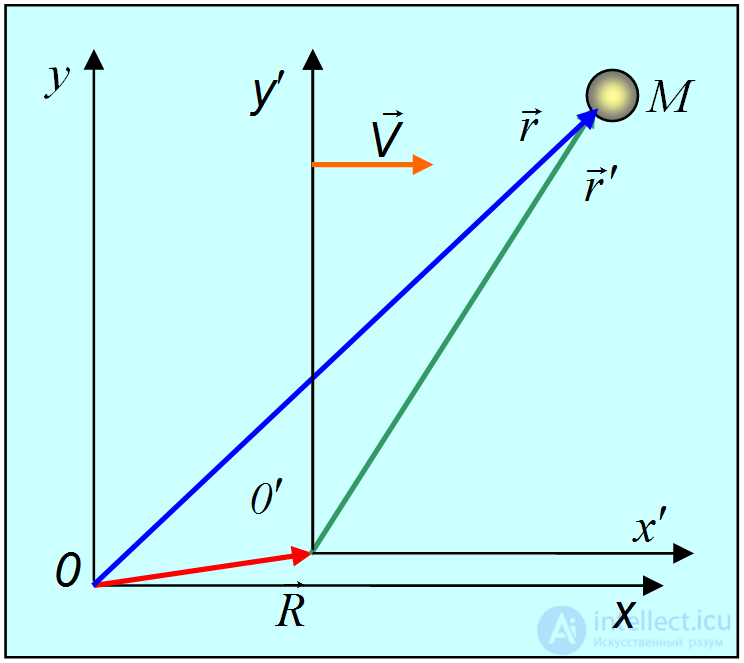
Рис. 3.31. Движение тел в двух разных системах отсчета
Все величины, относящиеся к этой системе отсчета, мы будем снабжать знаком штриха (x', y', z' и т.п.). Положение начала отсчета 0' относительно системы 0 характеризуется радиус-вектором 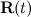 . Рассмотрим движение материальной точки М. Ее положение относительно системы 0 задается радиус-вектором
. Рассмотрим движение материальной точки М. Ее положение относительно системы 0 задается радиус-вектором 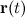 , а относительно 0' — радиус-вектором
, а относительно 0' — радиус-вектором 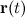 . Исходя из правил сложения векторов, можем написать
. Исходя из правил сложения векторов, можем написать
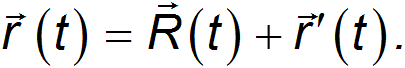
Дифференцируем данное соотношение по времени и получаем:
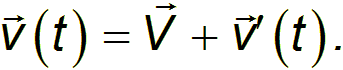
Здесь  ,
, 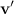 — скорость материальной точки М относительно систем 0 и 0', соответственно. Вектор V — это скорость «штрихованной» системы отсчета относительно «нештрихованной». Мы получили закон сложения скоростей классической механики:
— скорость материальной точки М относительно систем 0 и 0', соответственно. Вектор V — это скорость «штрихованной» системы отсчета относительно «нештрихованной». Мы получили закон сложения скоростей классической механики:
Скорость v точки относительно системы 0 может быть представлена как векторная сумма ее скорости 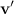 относительно системы 0' и скорости V системы 0' относительно системы 0.
относительно системы 0' и скорости V системы 0' относительно системы 0.
Если система 0' движется относительно 0 прямолинейно и равномерно, то V не зависит от времени. Дифференцируя полученный закон сложения скоростей по времени, находим, что ускорения точки М относительно обеих систем отсчета одинаковы:
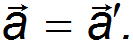
Если 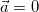 , то и
, то и 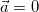 , то есть закон инерции Галилея выполняется в обеих системах отсчета. Стало быть, если система 0 инерциальная, то инерциальной будет и система 0'.
, то есть закон инерции Галилея выполняется в обеих системах отсчета. Стало быть, если система 0 инерциальная, то инерциальной будет и система 0'.
Законы механики имеют одинаковый вид во всех инерциальных системах отсчета, которые являются физически эквивалентными (не отличимыми друг от друга). Это и составляет принцип относительности Галилея:
Уравнения, выражающие законы природы, инвариантны по отношению к преобразованиям координат и времени от одной инерциальной системы отсчета к другой.
Одинаковость вида уравнений движения во всех инерциальных системах отсчета не означает, разумеется, что одно и тоже движение выглядит одинаково в любой инерциальной системе, так как кроме уравнений движения (законов Ньютона) закон движения тела определяется также начальными условиями, которые, в движущихся относительно друг друга инерциальных системах отсчета, естественно, различны: начальные скорости разные
Если начальные условия различны, то одно и то же движение тела выглядит по-разному в различных инерциальных системах отсчета. В качестве примера рассмотрим падение мячика с верхушки мачты корабля (рис. 3.32). С точки зрения наблюдателя на корабле мячик движется прямолинейно: падает с нулевой начальной скоростью по вертикали вниз. В то время как для наблюдателя, находящегося на берегу, траектория мяча — парабола: мячик имеет отличную от нуля горизонтальную начальную скорость.
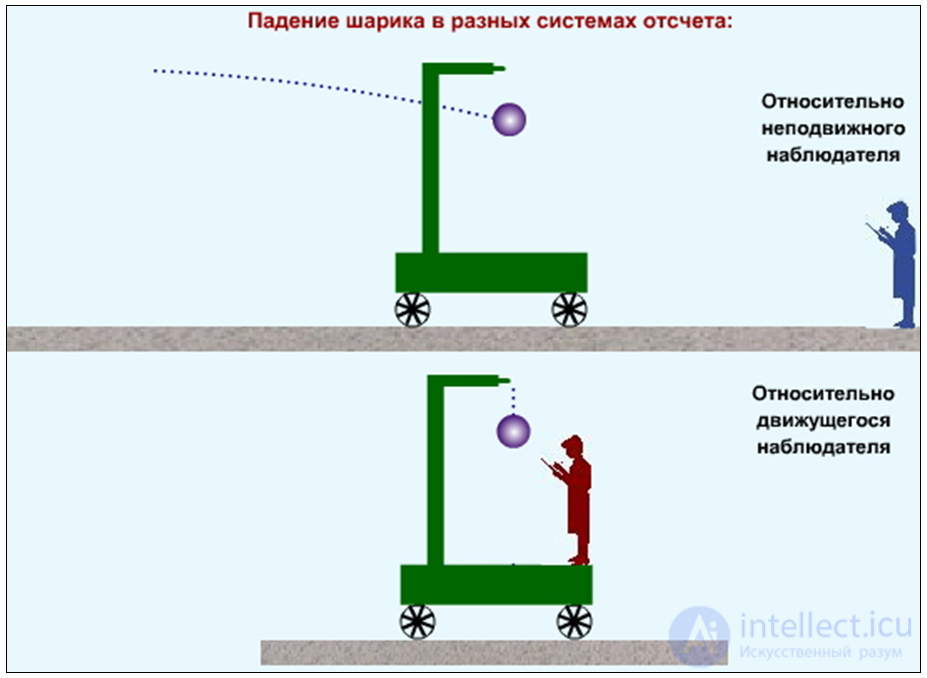
Рис. 3.32. Движение тела в разных инерциальных системах отсчета
Связь координат точки в разных системах отсчета дается полученным выше уравнением
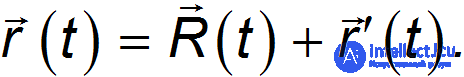
Его можно записать в виде уравнений для компонент вдоль осей координат. Для упрощения формул часто поступают следующим образом. Во-первых, оси систем выбираются параллельными, причем ось х указывает направление движения системы 0' относительно системы 0. Во-вторых, за начало отсчета времени выбирают момент, когда совпадали начала координат обеих систем. Тогда
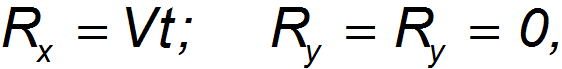
и мы получаем преобразования Галилея
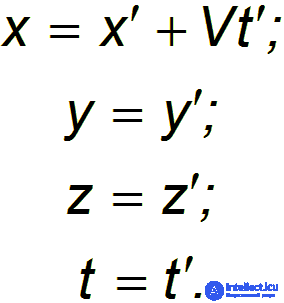
Мы дополнили преобразования пространственных координат равенством времен 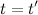 в обеих системах отсчета, чтобы подчеркнуть, что в классической механике время предполагается абсолютным, оно одно и то же в обеих системах отсчета.
в обеих системах отсчета, чтобы подчеркнуть, что в классической механике время предполагается абсолютным, оно одно и то же в обеих системах отсчета.
Переход в другую систему отсчета — один из методов решения ряда физических задач. Приведем пример.
Пример. Катер, двигаясь вниз по реке, обогнал плот в пункте А. Через время 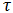 после этого он повернул обратно и затем встретил плот на расстоянии
после этого он повернул обратно и затем встретил плот на расстоянии  ниже пункта А. Найти скорость течения, если скорость катера относительно воды постоянна.
ниже пункта А. Найти скорость течения, если скорость катера относительно воды постоянна.
В данной задаче рассматривается одномерное движение частиц (плот и катер можно рассматривать как частицы, поскольку они движутся поступательно). Задачу целесообразно решить двумя способами, отличающимися выбором системы отсчета.
Способ 1. В системе отсчета, связанной с берегом реки (рис. 3.33), необходимо выразить пути, пройденные плотом и катером, через скорость течения реки  и катера относительно воды
и катера относительно воды  и времена движения катера вниз
и времена движения катера вниз 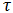 и вверх по течению
и вверх по течению 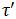 соответственно. После необходимых преобразований становится ясно, что
соответственно. После необходимых преобразований становится ясно, что 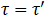 и , следовательно, общее время движения катера, (а, следовательно, и плота) равно
и , следовательно, общее время движения катера, (а, следовательно, и плота) равно 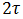 . Очевидно, что за это время плот прошел расстояние
. Очевидно, что за это время плот прошел расстояние 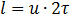 , откуда находится скорость течения
, откуда находится скорость течения  .
.
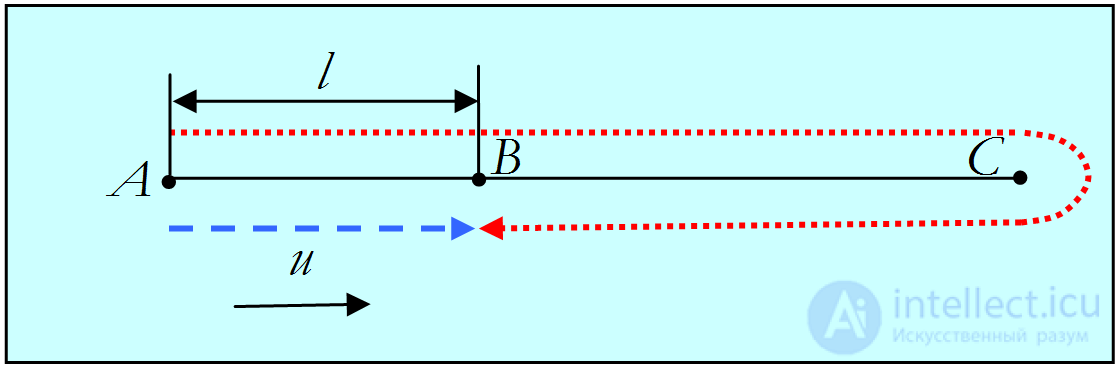
Рис. 3.33. Движение катера вниз и вверх по течению реки
В системе отсчета, связанной с берегом, путь 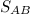 , пройденный плотом, равен
, пройденный плотом, равен
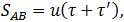
а путь 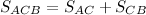 , пройденный катером, равен
, пройденный катером, равен
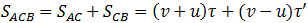
Учитывая, что
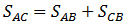
после преобразований получаем
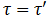
Следовательно, время движения плота равно 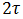 , откуда скорость течения
, откуда скорость течения
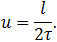
Способ 2. В системе отсчета, связанной с плотом, который относительно берегов движется со скоростью течения реки, очевидно, что время движения катера вниз и вверх по течению одинаково, и равно 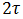 . Поэтому общее время движения равно
. Поэтому общее время движения равно 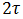 , и мы вновь получаем тот же результат но гораздо более простым путем.
, и мы вновь получаем тот же результат но гораздо более простым путем.
Сопоставление двух способов решения показывает важность обоснованного выбора системы отсчета.
Исследование, описанное в статье про динамика материальной точки, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое динамика материальной точки, принцип инерции галилея, законы ньютона, механические силы, закон сохранения импульса, реактивное движение, принцип относительности галилея и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Физические основы механики
Комментарии
Оставить комментарий
Физические основы механики
Термины: Физические основы механики