Лекция
Привет, сегодня поговорим про игра с двумя пальцами морра, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое игра с двумя пальцами морра , настоятельно рекомендую прочитать все из категории Математические методы исследования операций .Теория игр и расписаний..
Пример. Игра с двумя пальцами Морра.
Два игрока одновременно показывают один или два пальца и называют цифру один или два, угадывая число пальцев, показанных противником. Если оба угадали, игра заканчивается вничью, выигрыш обоих игроков – нуль, если оба не угадали – тоже ничья. Если угадал только один игрок, угадавший получает выигрыш равный суммарному числу показанных пальцев. У каждого четыре стратегии:
1) {1,1}; 2){1,2}; 3){2,1}; 4){2,2}.

Пример. Военная игра.
Есть две позиции и два противника – полковник и генерал. У полковника 4 полка, у генерала – 3. Каждый хочет занять позиции. Взятые позиции оцениваются единицей. Каждый может посылать на любую позицию целое число полков или совсем не посылать. Позиция считается занятой тем, кто послал на нее больше полков и выигрыш составляет единицу плюс число полков противника, не занявшего позицию. Если у позиции оказывается равное число полков, выигрыш составляет нуль. Общий выигрыш считается по двум позициям. Выигрыш одного считается потерей другого.
У полковника есть такие чистые стратегии:
1. {4,0}; 2. {0,4}; 3. {3,1}; 4. {1,3}; 5. {2,2}
У генерала есть чистые стратегии:
1. {3,0}; 2. {0,3}; 3. {2,1}; 4. {1,2}
Матрица игры:
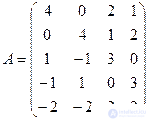
Пример.
Две компании А и В продают лекарства от гриппа.
Компания А рекламирует продукцию:
- на радио (А1)
- на телевидении (А2)
- в газетах (А3) .
Компания В действует также (В1,В2,В3), а кроме того, рассылают рекламные брошюры (В4).
Каждая из компаний своими действиями может привлечь на свою сторону некоторый процент клиентов конкурирующей компании. Это задано матрицей игры:
|
|
В1 |
В2 |
В3 |
В4 |
Минимумы строк |
|
А1 |
8 |
-2 |
9 |
-3 |
-3 |
|
А2 |
6 |
5 |
6 |
8 |
5Максимин |
|
А3 |
-2 |
4 |
-9 |
5 |
-9 |
|
Максимумы столбцов |
8 |
5Минимакс |
9 |
8 |
|
(Игры с седловой точкой 5%)
Смешанные стратегии.
Существенную долю матричных игр составляют игры без седловой точки, в которых нижняя цена игры 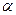 строго меньше верхней цены
строго меньше верхней цены 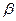 . . Если такая игра состоит только из одной партии, то есть каждый игрок делает по ходу, то осторожность поведения мотивирует выбор игроком А одной из своих максиминныхстратегий, а игроком В – одной из своих минимаксных. Тогда игрок А обеспечивает себе выигрыш, не менее
. . Если такая игра состоит только из одной партии, то есть каждый игрок делает по ходу, то осторожность поведения мотивирует выбор игроком А одной из своих максиминныхстратегий, а игроком В – одной из своих минимаксных. Тогда игрок А обеспечивает себе выигрыш, не менее 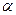 , а игрок В гарантирует, что выигрыш игрока А будет не более чем
, а игрок В гарантирует, что выигрыш игрока А будет не более чем 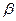 .
.
А как действовать, если игра повторяется многократно? Какой образ действий выбрать, чтобы увеличить минимальный гарантированный выигрыш игрока А 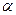 иуменьшить гарантированный проигрыш игрока В
иуменьшить гарантированный проигрыш игрока В 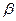 ? Фактически это есть вопрос о разделе разности
? Фактически это есть вопрос о разделе разности 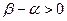 между игроками А и В с максимальной пользой для каждого из них. Такой способ есть и он состоит в случайном чередовании чистых стратегий.
между игроками А и В с максимальной пользой для каждого из них. Такой способ есть и он состоит в случайном чередовании чистых стратегий.
Стратегия игрока, состоящая в случайном выборе одной из его чистых стратегий, называется смешанной стратегией. Об этом говорит сайт https://intellect.icu . Таким образом смешанная стратегия игрока – это дискретная случайная величина, значениями которой являются номера его чистых стратегий. Обозначим через P и Q смешанные стратегии игроков А и В соответственно. Тогда смешанная стратегия P задается законом распределения:
|
1 |
… |
i |
… |
m |
|
p1 |
… |
pi |
… |
pm |
где pi0 – вероятность применения игроком А чистой стратегии Ai, и p1+p2+…+pi+…+pm=1, как сумма вероятностей несовместных событий (состоящих в выборе одной из чистых стратегий) полной группы. Смешанная стратегия Q
|
1 |
… |
j |
… |
n |
|
q1 |
… |
qj |
… |
qn |
где qj0 – вероятность выбора игроком В чистой стратегии qj и q1+q2+…+qj+…+qn=1.
Чистая стратегия очевидно есть частный случай смешанной для pi или qj=1.
Средний выигрыш игрока А в игре со смешанной стратегией выражается математическим ожиданием его выигрышей
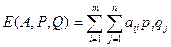
По аналогии с играми, имеющими седловую точку, вводится также определение: оптимальными смешанными стратегиями называются такие наборы P;Q , которые удовлетворяют равенству
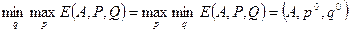
Величина E(A,p0,q0) называется ценой игры и обозначается буквой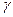 . Цена смешанной игры удовлетворяет условию:
. Цена смешанной игры удовлетворяет условию: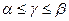
Оптимальные смешанные стратегии и цена смешанной игры (P0,Q0, ) называются решением матричной игры.
) называются решением матричной игры.
Теорема фон Неймана (основная теорема матричных игр). Любая матричная игра имеет хотя бы одно решение в смешанных стратегиях, то есть существуют цена игры в смешанных стратегиях и оптимальные смешанные стратегии P0 и Q0 соответственно игроков А и В.
Оптимальная смешанная стратегия является равновесной такой игры, то есть никакому игроку нет смысла от нее отклоняться.
Решение игры (2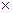 2)
2)
Пусть матрица игры 2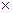 2 не имеет седловой точки. Записывая цену игры и присоединяя к ней условие нормировки вероятности имеем две системы уравнений:
2 не имеет седловой точки. Записывая цену игры и присоединяя к ней условие нормировки вероятности имеем две системы уравнений:
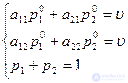
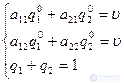
Отсюда легко находится решение: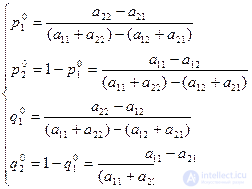
а цена игры определяется как:
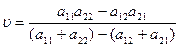
Графическое решение игр.
Рассмотрим игру 2хn:
|
|
q1 B1 |
q2 B2 |
… |
qn Bn |
|
p1, A1 |
a11 |
a12 |
… |
a1n |
|
p2=1-p1, A2 |
a21 |
a22 |
… |
a2n |
Игра предполагает, что игрок А смешивает стратегии А1 и А2 с вероятностями р1 и р2=1-р1. Игрок В смешивает стратегии В1, В2, …, Вn с вероятностями q1,q2,…,qn, q1+q2+…+qn=1. Ожидаемый выигрыш игрока А, соответствующий j-й чистой стратегии игрока В есть
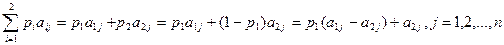
Следовательно игрок А ищет величину р1, которая максимизирует минимум ожидаемых выигрышей
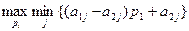
Рассмотрим конкретную игру 2х4.
|
|
B1 |
B2 |
B3 |
B4 |
|
A1 |
2 |
2 |
3 |
-1 |
|
A2 |
4 |
3 |
2 |
6 |
Седловой точки нет, следовательно, игра решается в смешанных стратегиях. Ожидаемые выигрыши игрока А, соответствующие чистым стратегиям игрока В, таковы
|
Чистые стратегии игрока В |
Ожидаемые выигрыши игрока А |
|
1 2 3 4 |
-2р1+4 -р1+3 р1+2 -7р1+6 |
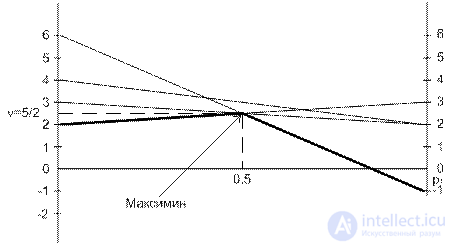
Изобразим четыре прямых, соответствующих чистым стратегиям игрока В. Чтобы определить наилучший результат из наихудших, построим нижнюю огибающую. Она представляет наихудший (минимальный) выигрыш игрока А, независимо от поведения игрока В. Максиминному решению соответствует максимум нижней огибающей в точке 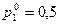 . Эта точка является пересечением прямых 3 и 4. Следовательно оптимальное решение для игрока А есть смешивание стратегий А1 и А2 с вероятностями 0,5 и 0,5. Цену игры можно найти графически а можно из уравнений прямых 3 и 4:
. Эта точка является пересечением прямых 3 и 4. Следовательно оптимальное решение для игрока А есть смешивание стратегий А1 и А2 с вероятностями 0,5 и 0,5. Цену игры можно найти графически а можно из уравнений прямых 3 и 4:
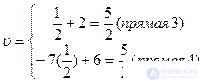
Оптимальная смешанная стратегия игрока В определяется двумя стратегиями, которые формируют нижнюю огибающую. Это значит, что игрок В может смешивать стратегии В3 и В4, то есть q1=q2=0, q4=1-q3.
Ожидаемые платежи игрока В:

|
Чистые стратегии игрока А |
Ожидаемые платежи игрока В |
|
1 2
|
4q3-1 -4q3+6 |
 Наилучшее решение из наихудших для В – точка минимума верхней огибающей.
Наилучшее решение из наихудших для В – точка минимума верхней огибающей.
4q3-1=-4q3+6, q3=7/8
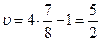
Для игры mx2 решение находится аналогично. Главное отличие состоит в том, что здесь строятся графики функций, представляющие ожидаемые платежи второго игрока, соответствующие чистым стратегиям игрока А. Потом ведется поиск минимаксной точки верхней огибающей.
Матричная игра как задача линейного программирования.
Рассмотрим матричную игру заданную матрицей:
|
В А |
1 |
2 |
… |
j |
… |
n |
|
1 |
a11 |
a12 |
… |
a1j |
… |
a1n |
|
2 |
a21 |
a22 |
… |
a2j |
… |
a2n |
|
… |
… |
… |
… |
… |
… |
… |
|
i |
ai1 |
ai2 |
… |
aij |
|
ain |
|
… |
… |
… |
… |
… |
… |
… |
|
m |
am1 |
am2 |
… |
amj |
… |
amn |
Будем считать, что все элементы платежной матрицы неотрицательны (если это не так, можно ко всем элементам матрицы добавить некоторое достаточно большое число L, переводящее платежи в область неотрицательных значений). Цена игры при этом увеличится на L, а решение задачи не изменится. Поэтому можно принять, что  .
.
Пусть платежная матрица игры не содержит седловой точки , следовательно игра решается в смешанных стратегиях:
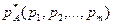
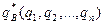
Применение игроком А оптимальной смешенной стратегии 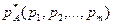 гарантирует ему, независимо от поведения игрока В, выигрыш, не меньший цены игры υ.
гарантирует ему, независимо от поведения игрока В, выигрыш, не меньший цены игры υ.
.
Надеюсь, эта статья об увлекательном мире игра с двумя пальцами морра, была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое игра с двумя пальцами морра и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические методы исследования операций .Теория игр и расписаний.
Комментарии
Оставить комментарий
Математические методы исследования операций .Теория игр и расписаний.
Термины: Математические методы исследования операций .Теория игр и расписаний.