Лекция
Привет, Вы узнаете о том , что такое ТЕОРИЯ ТЕХНИЧЕСКОЙ ДИАГНОСТИКИ, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое ТЕОРИЯ ТЕХНИЧЕСКОЙ ДИАГНОСТИКИ, техническая диагностика , настоятельно рекомендую прочитать все из категории Диагностика, обслуживание и ремонт электронной и радиоаппаратуры.
Наиболее важным показателем надежности является отсутствие отказов во время функционирования (работы) технической системы. техническая диагностика , благодаря раннему обнаружению дефектов и неисправностей, позволяет устранить подобные отказы в процессе технического обслуживания, что повышает надежность и эффективность эксплуатации, а также дает возможность эксплуатации технических систем ответственного назначения по состоянию. При эксплуатации по состоянию каждый экземпляр эксплуатируется до предельного состояния в соответствии с рекомендациями системы технической диагностики.
Основной задачей технической диагностики является распознавание состояния технической системы в условиях ограниченной информации.
Теоретическим фундаментом для решения основной задачи технической диагностики следует считать общую теорию распознавания образов. Техническая диагностика изучает алгоритмы распознавания применительно к задачам диагностики, которые обычно могут рассматриваться как задачи классификации.
Алгоритмы распознавания в технической диагностике частично основываются на диагностических моделях, устанавливающих связь между состояниями технической системы и их отображениями в пространстве диагностических сигналов. Важной частью проблемы распознавания являются правила принятия решений. Для принятия обоснованного решения целесообразно привлекать методы теории статических решений.
Решение задач технической диагностики всегда связано с прогнозированием надежности на ближайший период эксплуатации (до следующего технического осмотра). Здесь решения должны основываться на моделях отказов, изучаемых в теории надежности.
Вторым важным направлением технической диагностики является теория контролеспособности. Контролеспособностью называется свойство изделия обеспечивать достоверную оценку его технического состояния и ранее обнаружение неисправностей и отказов. Контролеспособность создается конструкцией изделия и принятой системой технической диагностики.
Состояние системы описывается совокупностью (множеством) определяющих ее параметров (признаков).
Распознавание состояния системы – отнесение состояния системы к одному из возможных классов (диагнозов). Число диагнозов (классов, типичных состояний, эталонов) зависит от особенностей задачи и целей исследования.
Часто требуется провести выбор одного из двух диагнозов (дифференциальная диагностика или дихотомия), например, «исправное состояние» и «неисправное состояние». В других случаях необходимо более подробно охарактеризовать неисправное состояние. В большинстве задач технической диагностики диагнозы (классы) устанавливаются заранее, и в этих условиях задачу распознавания часто называют задачей классификации.
Совокупность последовательных действий в процессе распознавания называется алгоритмом распознавания. Существенной частью процесса распознавания является выбор параметров, описывающих состояние системы. Они должны быть достаточно информативны, чтобы при выбранном числе диагнозов процесс разделения (распознавания) мог быть осуществлен.
Математическая постановка задачи. В задачах диагностики состояния системы часто описывается с помощью комплекса признаков
K = (k1, k2, …, kj, …, kν), (2.1)
где kj – признак, имеющий mj разрядов.
Каждый разряд (интервал) признака kj обозначается kjs. Фактически наблюдаемое состояние соответствует определенной реализации признака, что отмечается верхним индексом *.
В общем случае каждый экземпляр системы соответствует некоторой реализации комплекса признаков:
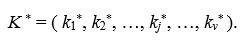(2.2)
Во многих алгоритмах распознавания удобно характеризовать систему параметрами хj, образующими ν-мерный вектор или точку в ν-мерном пространстве:
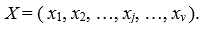(2.3)
В большинстве случаев параметры хj имеют непрерывное распределение.
С помощью признака kj получается дискретное описание, тогда как параметр хj дает непрерывное описание. При непрерывном описании обычно требуется значительно больший объем предварительной информации, но описание получается более точным. Если, однако, известны статические законы распределения параметра, то необходимый объем предварительной информации сокращается.
Принципиальных отличий при описании системы с помощью признаков или параметров нет, и в дальнейшем будут использованы оба вида описания.
Как указывалось, в задачах технической диагностики возможные состояния системы – диагнозы Di – считаются известными.
Существуют два основных подхода к задаче распознавания: вероятностный и детерминистский. Постановка задачи при вероятностных методах распознавания такова. Имеется система, которая находится в одном из n случайных состояний Di. Известна совокупность признаков (параметров), каждый из которых с определенной вероятностью характеризует состояние системы. Требуется построить решающее правило, с помощью которого предъявленная (диагностируемая) совокупность признаков была бы отнесена к одному из возможных состояний (диагнозов). Желательно также оценить достоверность принятого решения и степень риска ошибочного решения.
При детерминистских методах распознавания удобно формулировать задачу на геометрическом языке. Если система характеризуется ν-мерным вектором Х, то любое состояние системы представляет собой точку в ν-мерном пространстве параметров (признаков). Предполагается, что диагноз Di соответствует некоторой области рассматриваемого пространства признаков. Требуется найти решающее правило, в соответствии с которым предъявленный вектор Х * (диагностируемый объект) будет отнесен к определенной области диагноза. Таким образом, задача сводит к разделению пространства признаков на области диагнозов.
При детерминистском подходе области диагнозов обычно считаются «непересекающимися», т.е. вероятность одного диагноза (в область которого попадает точка) равна единице, вероятность других равна нулю. Подобным образом предполагается, что и каждый признак либо встречается при данном диагнозе, либо отсутствует.
Вероятностный и детерминистский подходы не имеют принципиальных различий. Более общими являются вероятностные методы, но они часто требуют и значительно большего объема предварительной информации. Детерминистские подходы более кратко описывают существенные стороны процесса распознавания, меньше зависят от избыточной, малоценной информации, больше соответствуют логике мышления человека.
Основное преимущество статистических методов распознавания состоит в возможности одновременного учета признаков различной физической природы, так как они характеризуются безмерными величинами – вероятностями их появления при различных состояниях системы.
В большинстве методов распознавания делается естественное предположение, что изображения объектов одного класса (образа) более близки друг другу, чем изображения разных классов. Метрические методы основаны на количественной оценке этой близости. В качестве изображения объекта принимается точка в пространстве признаков, мерой близости считается расстояние между точками.
Экспериментальные данные, обеспечивающие получение статических зависимостей, описывающих связи между нарушением в конструкции объекта и измеряемым параметром, можно получить только для объектов массового производства. В некоторых случаях такие зависимости получить невозможно. Тогда один из способов получения необходимой информации – использование уравнений, описывающих процессы в элементах объекта, в том числе и процесс развития неисправности, т.е. математических моделей объекта. В результате расчетов с использованием, как уравнений объекта, так и уравнений неисправности, устанавливается связь между степенью развития неисправности и поведением измеряемых параметров, т.е. информация, необходимая для формирования алгоритмов систем функционального диагностирования (СФД).
Математические модели (ММ) элементов системы. Математические модели (ММ) элемента системы – это совокупность дифференциальных и алгебраических уравнений, эмпирических формул, таблиц, графиков, описывающих характеристики элемента (агрегата, узла), т.е. связи между внутренними и внешними управляющими и возмущающими параметрами :
F (x, y, u) = 0,(2.4)
где x – вектор параметров объекта; y – вектор управляющих воздействий; u – вектор возмущающих воздействий.
Для задач функциональной диагностики ММ применяются при моделировании (численный эксперимент) развития той или иной неисправности с целью выявления диагностических признаков и проверки эффективности работы технических средств диагностики. Существуют ММ нормально функционирующего элемента и ММ, в которые заложены данные развития той или иной неисправности. Последние ММ определяют связи между изменением конструктивных параметров, вызывающих ненормальную работу объекта, и измеряемыми параметрами. Эти два типа ММ могут существенно отличаться, так как появление неисправности может изменить структуру объекта, а также приводит к появлению новой переменной, характеризующей степень развития неисправности.
По способу формирования ММ можно разделить на аналитические, эмпирические и полуэмпирические.
По форме записи используемых уравнений, а точнее – по глубине описания процесса, все ММ делятся на линейные и нелинейные. Кроме того, в зависимости от характера исходных данных, методов их обработки при формировании ММ, полуэмпирические и эмпирические ММ делятся на детерминированные и стохастические. Соотношение между характерными размерами исследуемого объекта и длиной распространяющихся в объекте волн позволяет определить необходимость использования ММ, описывающих объект как систему с распределенными или сосредоточенными параметрами.
Из соотношения между характерной постоянной времени системы и временем развития неисправности выясняется вопрос о необходимости учета динамических процессов в системе или возможности ограничиться квазистатическим подходом, т.е. использовать статические ММ. Аналитические модели содержат дифференциальные уравнения, граничные и начальные условия к ним, алгебраические зависимости, полученные из общих физических закономерностей. Преимущество аналитических ММ – их общность, возможность описания процессов в достаточно широком круге объектов. Существенные недостатки этих ММ – невысока точность описания свойств многих объектов из-за сложности реальных процессов и отсутствия для них достаточно точных аналитических зависимостей, а также трудоемкость нахождения решений, описывающих более или менее сложные процессы, даже с использованием современных ЭВМ.
Эмпирические (экспериментальные) модели обладают достаточной точностью, однако для получения функциональных связей между параметрами процесса в объекте и внешними возмущениями или регулирующими параметрами необходим большой объем экспериментов. Об этом говорит сайт https://intellect.icu . Результаты экспериментов не всегда можно распространить на подобные объекты. Для получения обобщенных экспериментальных зависимостей, пригодных для описания процессов в ряде однотипных объектов, необходимо использовать методы теории подобия.
Наибольшее распространение получили смешанные полуэмпирические ММ, при формировании которых используются как общие физические закономерности, так и данные экспериментов, которые позволяют учесть многие детали процесса, не учитываемые аналитическими ММ.
В случае формирования чисто эмпирических и полуэмпирических ММ для выбора наиболее удобной формы уравнений и определения их коэффициентов используются методы идентификации. Все перечисленные виды ММ находят применение при построении ТСД.
В нелинейных уравнениях, записываемых в форме (2.4), переменные x, y, u и их производные входят в виде произведений, степеней, трансцендентных функций и т.д. Линейные (линеаризированные) уравнения имеют форму
A(s) x = φ (y, u),2.5)
где A(s) – квадратная матрица, коэффициенты которой – многочлены по s; s = d / d t – оператор дифференцирования. Для линейных уравнений существуют хорошо разработанные методы решения, для них применим принцип суперпозиции; для нелинейных уравнений таких общих методов решений нет. Для большинства объектов, включающих ТСД, изменения параметров процессов в достаточно широком диапазоне описываются нелинейными зависимостями.
В зависимости от класса решаемой задачи один и тот же объект можно описать как нелинейными, так и линейными (линеаризованными) уравнениями, и если позволяют условия использования результатов решения, всегда имеет смысл хотя бы в первом приближении решать линейное (линеаризованное) уравнение.
При построении ММ допустимая степень упрощения модели определяется условиями функционирования системы.
Модели объектов, состоящих из связанных между собой элементов (агрегатов, устройств), формируются в два этапа: вначале создание ММ процессов в отдельных органах, агрегатах, узлах системы, а затем разработка ММ всей системы в целом с участием частных ММ отдельных подсистем и структуры связей между ними.
Математические модели систем. Для анализа состояния системы необходимо из ММ элементов собрать ММ всей системы, однако совокупность всех ММ, входящих в систему элементов, не является еще ММ системы. Для формирования замкнутой системы уравнений к уравнениям элементов необходимо добавить уравнения связей между параметрами входящих в ММ элементов. Если нарисовать схему системы, то все элементы окажутся связанными между собой, так как между ними осуществляется обмен информацией, рабочей средой, электрическим током, энергией и т.д. Для сечений или точек, связывающих между собой элементы, соблюдаются законы сохранения. В этом случае удобно применить аппарат теории цепей.
Модели неисправности. Под моделью неисправности понимается аналитическая или стохастическая зависимость, связывающая параметр, характеризующий степень развития неисправности, с временем или параметрами объекта диагностики. В качестве параметра, характеризующего неисправность, обычно используются первичные конструктивные параметры объекта, изменение которых является причиной появления признаков неисправности – изменения измеряемых параметров.
Как правило, используются ММ простых неисправностей, которые связаны с отклонением от нормального значения конструктивного параметра только одного агрегата объекта диагностики. Случай сложной неисправности, когда от нормального значения отклоняются одновременно (или в какой-то последовательности) конструктивные параметры ряда агрегатов, очень неудобен как для моделирования, так и для диагностики из-за многообразия возможных сочетаний параметров по величине, взаимной последовательности и т.д.
Если моделируются неисправности, нарушающие структуру моделируемой системы, то возможные неисправности должны быть заранее предусмотрены в ММ в виде отдельных структурных элементов.
Для воспроизведения картины развития неисправности с помощью ММ объекта в первую очередь необходимо определить, за какое характерное время развивается неисправность. Если это время соизмеримо или меньше характерной постоянной времени объекта, то необходимо использовать ММ объекта диагностики, в которой учтены динамические эффекты, т.е. члены с производными по времени. Для таких неисправностей закон изменения первичных признаков (отклонений параметров) задается как функция времени:
где Δ єi – отклонение i-го первичного конструктивного параметра, являющегося причиной развития данной неисправности; t н – момент начала отклонения первичного параметра за допустимые пределы; t к – момент окончания измерения первичных параметров; ƒi (t) – закон изменения во времени.
Возможен другой вариант соотношения характерных времен, когда время развития неисправности на много больше постоянной времени объекта. В этом случае можно использовать квазистационарную ММ объекта, в которой отсутствуют члены с производными по времени.
Решение проблемы прогнозирования и обеспечения технического ресурса предусматривает установление качественных и количественных закономерностей, определяющих ресурс оборудования, разработку методов оценки влияния различных факторов на ресурс. Решение проблемы открывает пути для научно обоснованного назначения ресурса, анализа и синтеза оборудования с учетом факторов надежности, для выбора конструктивных и технологических решений, обеспечивающих назначенные показатели долговечности.
Особый интерес представляет проблема прогнозирования индивидуального ресурса оборудования по результатам наблюдений за их состоянием в процессе эксплуатации. Предельные состояния оборудования являются результатом постепенного накопления повреждений в деталях, узлах и элементах.
Понятие ресурса. Технический ресурс (далее ресурс) – показатель долговечности, характеризующий запас возможной наработки объекта. Ресурсом называют наработку объекта от начала или возобновление эксплуатации до наступления предельного состояния.
В качестве меры продолжительности может быть выбран любой неубывающий параметр, характеризующий продолжительность эксплуатации объекта. Единицы для измерения ресурса выбирают применительно к каждой отрасли и к каждому классу машин, агрегатов и конструкций отдельно. С точки зрения теории и общей методологии наилучшей и универсальной единицей остается единица времени.
Исчисление ресурса в единицах времени позволяет поставить задачи прогнозирования в наиболее общей форме. Иногда используют дискретное время (например, число циклов или блоков включения-отключения). Если известно распределение по длительности циклов или блоков, а также распределение перерывов между ними, то пересчет на календарное время (или наоборот) не вызывает затруднений.
На стадии проектирования, когда объект еще не создан, его расчет, в том числе оценку ресурса, производят на основании нормативных документов, которые в свою очередь основаны (явно или неявно) на статистических данных о материалах, воздействиях и условиях эксплуатации аналогичных объектов. Таким образом, прогнозирование ресурса должно быть основано на вероятностных моделях. Назначенный ресурс задают определенным числом, соответствующим некоторой вероятности, с которой назначенный ресурс должен быть реализован в проектном объекте. Обычно используют понятие гамма-процентного ресурса – значение ресурса, обеспеченное с заданной вероятностью γ. Часто употребляют также понятие среднего ресурса и среднего срока службы. На стадии проектирования эти понятия означают математические ожидания соответственно ресурса и срока службы.
Прогнозирование ресурса и теория надежности. Прогнозирование ресурса – составная часть теории надежности оборудования. Под надежностью понимают способность технического объекта выполнять заданные функции в течение заданного отрезка времени или заданной наработки. В понятие надежности входит ряд свойств объекта: безотказность, долговечность, ремонтопригодность, сохраняемость. Одним из центральных понятий теории надежности является отказ – событие, которое заключается в нарушении работоспособного состояния объекта. В теории надежности отказ трактуют как случайное событие, принимая за один из основных показателей надежности вероятность безотказной работы в течение заданного отрезка времени или в пределах заданной наработки.
Ресурс и срок службы, будучи показателями долговечности, также принадлежать к числу основных понятий теории надежности. В простейшей ситуации, когда объект эксплуатируют до первого отказа, отождествляемого с предельными состояниями, безотказность работы объекта одновременно характеризует и его долговечность. Однако здесь рассматриваем более общий случай, когда после периода приработки интенсивность отказов снижена до минимума, причем система планово-профилактических мероприятий и технического обслуживания гарантирует предупреждение возможных отказов, или по меньшей мере, их быстрое устранение без длительных перерывов в эксплуатации и других нежелательных последствий. При этих условиях основными понятиями становятся предельное состояние, ресурс и срок службы.
Поведение объектов существенно зависит от их взаимодействия с окружающей средой, а также характера и интенсивности процессов эксплуатации. В теории надежности свойства материалов и воздействий приняты случайными, поэтому поведение объекта также носит случайный характер. Нормативные требования и технические условия эксплуатации накладывают определенные ограничения на эти параметры. Ограничения могут быть сформулированы в виде условия нахождения некоторого случайного вектора, зависящего от времени и характеризующего качество объекта, в заданной области. Отказам и предельным состояниям соответствуют выходы случайного вектора из области допустимых состояний. Таким образом, основная задача теории надежности – оценка вероятности безотказной работы на заданном отрезке времени – сведена к задаче о выбросах случайных процессов.
Интеллектуальные системы на основе искусственных нейронных сетей (ИНС) позволяют с успехом решать проблемы распознавания образов, выполнения прогнозов, оптимизации, ассоциативной памяти и управления.
Подобно биологической нейронной системе ИНС является вычислительной системой с огромным числом параллельно функционирующих простых процессоров с множеством связей. Модели ИНС в некоторой степени воспроизводят "организационные" принципы, свойственные мозгу человека.
По аналогии с биологическим нейроном искусственный нейрон также имеет синапсы, ячейку нейрона и аксон. Аксон - выходная связь нейрона, с которой сигнал поступает на синапсы следующих нейронов. Каждый синапс характеризуется величиной синаптической связи или ее весом wi, который по физическому смыслу эквивалентен электрической проводимости. В ячейке нейрона суммируются все входы, что определяет текущее состояние нейрона.
Текущее состояние нейрона определяется, как взвешенная сумма его входов:
Выход нейрона есть функция его состояния:
Нелинейная функция f называется активационной и может иметь различный вид. Одной из наиболее распространенных является нелинейная функция с насыщением, так называемая логистическая функция или сигмоид (т.е. функция S-образного вида):
ИНС может рассматриваться как направленный граф со взвешенными связями, в котором искусственные нейроны являются узлами. По архитектуре связей ИНС могут быть сгруппированы в два класса: сети прямого распространения, в которых графы не имеют петель, и рекуррентные сети, или сети с обратными связями.
Очевидно, что процесс функционирования ИНС, то есть сущность действий, которые она способна выполнять, зависит от величин синаптических связей, поэтому, задавшись определенной структурой ИНС, отвечающей какой-либо задаче, разработчик сети должен найти оптимальные значения всех весовых коэффициентов.
Этот этап называется обучением ИНС, и от того, насколько качественно он будет выполнен, зависит способность сети решать поставленные перед ней проблемы во время эксплуатации. На этапе обучения кроме параметра качества подбора весов важную роль играет время обучения. Как правило, эти два параметра связаны обратной зависимостью и их приходится выбирать на основе компромисса.
Наиболее распространенным алгоритмом обучения является алгоритм обратного распространения ошибки. Суть алгоритма - распространение сигналов ошибки от выходов ИНС к ее входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы.
Согласно методу наименьших квадратов, минимизируемой целевой функцией ошибки ИНС является величина:
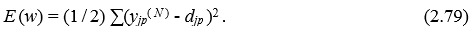
где yjp( N )– реальное выходное состояние нейрона j выходного слоя N нейронной сети при подаче на ее входы p-го образа; djp – идеальное (желаемое) выходное состояние этого нейрона.
Суммирование ведется по всем нейронам выходного слоя и по всем обрабатываемым сетью образам. Минимизация ведется методом градиентного спуска, что означает подстройку весовых коэффициентов следующим образом:
Здесь wij – весовой коэффициент синаптической связи, соединяющей i-ый нейрон слоя n-1 с j-ым нейроном слоя n, η – коэффициент скорости обучения, 0 < h <1.
В настоящее время метод ИНС активно используется для решения следующих энергетических и электротехнических задач: предсказание нагрузки; прогнозирование температуры окружающей среды с целью прогнозирования нагрузки; управление потоками электроэнергии в сетях; обеспечение максимальной мощности; регулирование напряжения; диагностика энергосистем с целью определения неисправностей; оптимизация размещения датчиков для контроля безопасности энергосистем; мониторинг безопасности энергосистем; обеспечение защиты трансформаторов; обеспечение устойчивости, оценка динамического состояния и диагностика генераторов; управление турбогенераторами; управление сетью генераторов; управление мощными переключательными системами; моделирование асинхронного двигателя; диагностика и мониторинг нагрева трансформаторов.
Рассмотрим основные возможные направления применения НС.
1. Применение НС для параметрического диагностирования элементов ЭМС. Он основан на сравнении математической модели конкретного элемента ЭМС (двигателя, трансформатора, кабельной линии, коммутационной аппаратуры) с моделью бездефектного элемента, т.е. в проверке принадлежности параметров состояний допустимым диапазонам их рассеивания. Выход параметра за пределы этих диапазонов должен свидетельствовать о наличии неисправности в соответствующем узле элемента ЭМС (рис.1).
2. Применение НС для прогнозирования параметров ЭМС. НС на основе разработанной определенной методики позволяет построить зависимость одного параметра от другого в виде полинома. Т.е она может позволить найти скрытые зависимости, одной величины от другой, которые невозможно определит методами прямых измерений. Так в асинхронном двигателе, путем установки специальных датчиков можно измерять, например, температуру его отдельных частей в статоре. А измерять температуру в отдельных частях ротора (магнитопроводе, обмотке и т.д.) затруднительно.
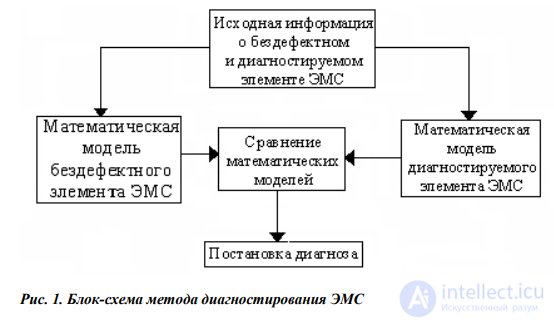
НС по разработанной тепловой модели двигателя поможет
определять температуру в заданных частях ротора при известных
значениях температуры в элементах статора. Вместо температуры
может быть любой другой параметр.
3. Применение НС для распознавания образов. Диагностика
неисправностей по многим критериям совпадает с задачей распознавания образов, поэтому, используя НС, можно достичь более
высоких результатов обнаружения неисправностей электрооборудования, входящего в ЭМС по сравнению с другими системами диагностики.
Состояние любого элемента ЭМС характеризуется большим
количеством параметров состояния (признаков), значения которых
можно получить, используя штатные средства измерения, или же
путем проведения дополнительных испытаний на работающем или
отключенном электрооборудовании.
НС позволяют проводить классификацию состояния электрооборудования, то есть отнести его состояние к одному из классов
состояний (исправное или неисправное с дефектом определенного
типа), определяемых по данному виду испытаний или измерений.
В системах диагностирования опытная информация о признаках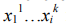 
каждого из n распознаваемых режимов функционирования может определяться как прямыми измерениями, так и на основе косвенных измерений (рис. 2).
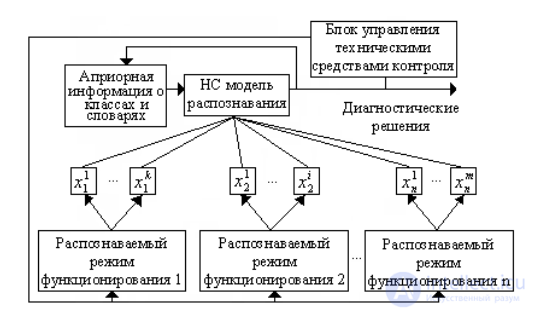
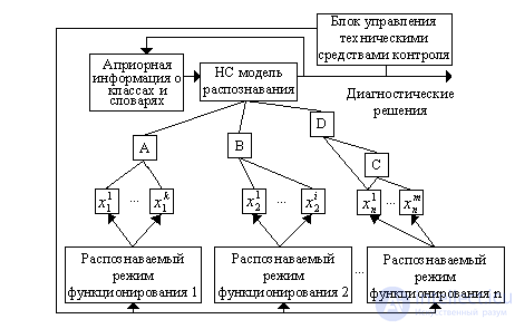
Рис. 2. Схема принятия решения в системах распознавания текущего технического состояния с прямыми (слева) и косвенными (справа) способами получения информации
Для последних используются специализированные локальные распознающие системы.
По данным n распознаваемых режимов функционирования определяются первичные признаки. На основе первичных признаков распознающие устройства второго уровня А, В, С, D определя-ют признаки второго уровня, и т.д. К последней группе относят
признаки, непосредственно используемые в процессе распознавания неизвестных объектов, т.е. признаки, входящие в рабочий словарь признаков системы распознавания.
Под классификацией (кластеризацией) в теории НС понимается разбиение множества входных сигналов на классы, при том, что
ни количество, ни признаки классов заранее не известны. После
обучения такая сеть способна определять, к какому классу относится входной сигнал. Сеть также может сигнализировать о том,
что входной сигнал не относится ни к одному из выделенных классов — это является признаком новых, отсутствующих в обучающей
выборке, данных. Таким образом, подобная сеть может выявлять
новые, неизвестные ранее классы сигналов. Соответствие между
классами, выделенными сетью, и классами, существующими в
предметной области, устанавливается человеком. Кластеризацию
осуществляют, например, нейронные сети Кохонена.
Число входов сети Кохонена - это число входных параметров,
а число выходов это число неисправностей. Число выходов меньше
числа входных комбинаций. Таким образом, сети Кохонена распознают неисправности, классифицируя их в зависимости от набора
входных параметров, которые изменяются от номинального до
критического (максимального или минимального) при котором
происходит отказ объекта.
Кластерный анализ - это совокупность методов, позволяющих
классифицировать многомерные наблюдения, каждый из которых
описывается набором характеристик (факторов) X1, X2,..., Xm – в
данном случае это может быть набором сигналов с различных датчиков (параметры состояния элемента ЭМС). Целью кластерного
анализа является образование групп, классов сходных между собой
объектов, которые принято называть кластерами. Слово "кластер"
(cluster) в переводе с английского означает: сгусток, пучок, группа.
Как родственные понятия в литературе используются: класс, таксон, сгущение. В ЭМС системах в качестве классов могут выступать в простейшем случае два: "исправен" и "неисправен". Как
правило, четкие границы каждого класса не указаны, но количество
их известно. При разработке системы диагностирования ЭМС кластерный анализ на основе обучающей выборки позволяет построить меру (расстояние) между двумя основными классами объектов
и определить "центры" каждого класса в пространстве характери-стик Х1, Х2,..., Xm, то есть сформировать ключевое правило собственно для задачи диагностики: по предъявляемому объекту вычисляются расстояния до каждого из классов ("исправен" и "неисправен"), и классифицируемый объект относится к классу, расстояние до которого оказывается минимальным.
В задачах классификации выходной элемент должен выдавать
сильный сигнал в случае, если данное наблюдение принадлежит к
интересующему нас классу, и слабый - в противоположном случае.
Иначе говоря, этот элемент должен стремиться смоделировать
функцию, равную единице в той области пространства объектов,
где располагаются объекты из нужного класса, и равную нулю вне
этой области.
Топология такой сети характеризуется тем, что количество
нейронов в выходном слое, как правило, равно количеству определяемых классов. При этом устанавливается соответствие между
выходом нейронной сети и классом, который он представляет. Когда сети предъявляется некий образ, на одном из ее выходов должен появиться признак того, что образ принадлежит этому классу.
В то же время на других выходах должен быть признак того, что
образ данному классу не принадлежит. Если на двух или более выходах есть признак принадлежности к классу, считается что сеть
«не уверена» в своем ответе.
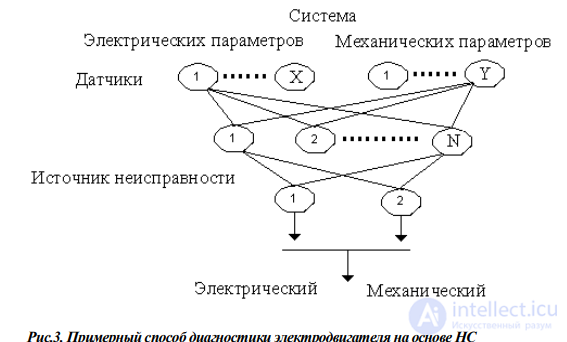
Приведем пример системы диагностики электродвигателя, построенной на основе НС (рис.3).
Экспертная система состояния двигателя имеет X датчиков,
контролирующих состояние его электрических параметров (ток,
напряжение, и т.д.) и Y датчиков, контролирующих состояние его
механических параметров (скорость, вибрация, температура и т.д.).
Каждому элементу входного слоя ставится в соответствие возможное значение параметра. Выходные данные задавались двоичным
вектором, в котором 1 соответствует наличию неисправности, а 0
— ее отсутствию. Такая система позволит определить источник
неисправности и ее характер.
4. Применение нейросетевых технологий для прогнозирования
технического состояния ЭМС. Способности нейронной сети к прогнозированию напрямую следуют из ее способности к обобщению
и выделению скрытых зависимостей между входными и выходными данными.
После обучения сеть способна предсказать будущее значение
некой последовательности на основе нескольких предыдущих значений или каких-то существующих в настоящий момент факторов.
Следует отметить, что прогнозирование возможно только тогда,
когда предыдущие изменения действительно в какой-то степени
предопределяют будущие
Если совокупность величин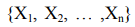 
представляет собой значения какого-либо параметра, изменяющегося во времени,
то такую совокупность называют временным рядом, при этом каждое значение соответствует значению параметра в конкретное время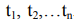 
. Задача прогнозирования в этом случае заключается в
определении значения измеряемой величины X в момент времени
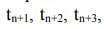, то есть для выполнения прогнозирования необходимо
выявить закономерность этого временного ряда.
На нейронных сетях задача прогнозирования формализуется
через задачу распознавания образов. Данных о прогнозируемой переменной за некоторый промежуток времени образуют образ, класс
которого определяется значением прогнозируемой переменной в
некоторый момент времени за пределами данного промежутка, т.е.
значением переменной через интервал прогнозирования. Метод
окон предполагает использование двух окон Wi и Wo с фиксиро-
ванными размерами n и m соответственно. Эти окна, способны перемещаться с некоторым шагом по временной последовательности исторических данных, начиная с первого элемента, и предназначены для доступа к данным временного ряда, причем первое окно Wi, получив такие данные, передает их на вход нейронной сети, а второе - Wo - на выход. Получающаяся на каждом шаге пара используется как элемент обучающей выборки (распознаваемый образ, или наблюдение). Каждый следующий вектор получается в результате сдвига окон Wi и Wo вправо на один элемент. Нейронная сеть, обучаясь на этих наблюдениях и соответственно настраивая свои коэффициенты, пытается извлечь эти закономерности и сформировать в результате требуемую функцию прогноза. Как было сказано выше, результатом прогноза с использованием НС является класс, к которому принадлежит переменная, а не ее конкретное значение. Формирование классов должно проводиться в зависимости от того каковы цели прогнозирования. Общий подход состоит в том, что область определения прогнозируемой переменной разбивается на классы в соответствии с необходимой точностью прогнозирования. Практическая реализация перечисленных свойств НС позволит создать совершенно новую систему для автоматического диагностирования и прогнозирования состояний подсистем ЭМС
Контрольные вопросы
1 Что является основной задачей технической диагностики?
2 Что называется алгоритмом распознавания?
3 Чем отличаются вероятностный и детерминистский подход к задаче распознавания технического состояния оборудования?
4 Чем отличаются аналитические, эмпирические и полуэмпирические способы формирования математических моделей объектов и систем диагностирования?
5 Объясните закономерности поведения «кривой жизни» технических изделий.
6 Что такое «мера повреждений» и как она определяется?
7 Что такое «плотность гамма-распределения»?
8 Поясните график многостадийной модели процесса накопления повреждений.
9 Что такое «технический ресурс» оборудования?
10 В чем отличие нейронных сетей от обычных вычислительных систем?
СПИСОК ЛИТЕРАТУРЫ
1. Ляхомский А.В., Плащанский Л.А., Чеботаев Н.И. и др. Электрификация горного производства. В 2-х томах /Под ред. Л.А. Пучкова, Г.Г. Пивняка, М.: Издательство МГГУ, 2007. – 1104 с.
Исследование, описанное в статье про ТЕОРИЯ ТЕХНИЧЕСКОЙ ДИАГНОСТИКИ, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое ТЕОРИЯ ТЕХНИЧЕСКОЙ ДИАГНОСТИКИ, техническая диагностика и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Диагностика, обслуживание и ремонт электронной и радиоаппаратуры
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Диагностика, обслуживание и ремонт электронной и радиоаппаратуры
Термины: Диагностика, обслуживание и ремонт электронной и радиоаппаратуры