Квадратное уравнение ax² + bx + c (a ≠ 0) и теорема Виета (уравнение второй степени)

Привет, сегодня поговорим про квадратное уравнение, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое квадратное уравнение, ax² + bx + c a ≠ 0, теорема виета, уравнение второй степени, дискриминант , настоятельно рекомендую прочитать все из категории СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА.

квадратное уравнение — алгебраическое уравнение общего вида

где — неизвестное, , , — коэффициенты, причем

Выражение называют квадратным трехчленом .

Корень — это значение переменной , обращающее квадратный трехчлен в ноль, а квадратное уравнение в верное числовое равенство.

Элементы квадратного уравнения имеют собственные названия :

• называют первым или старшим коэффициентом,
• называют вторым, средним коэффициентом или коэффициентом при ,
• называют свободным членом.

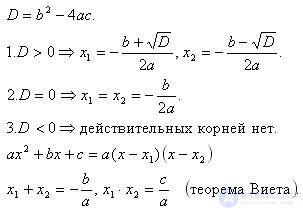
Приведенным называют квадратное уравнение, в котором старший коэффициент равен единице . Такое уравнение может быть получено делением всего выражения на старший коэффициент :

Полным называют такое квадратное уравнение, все коэффициенты которого отличны от нуля.

Неполным называется такое квадратное уравнение, в котором хотя бы один из коэффициентов, кроме старшего (либо второй коэффициент, либо свободный член), равен нулю.

Квадратное уравнение является разрешимым в радикалах, то есть его корни могут быть выражены через коэффициенты в общем виде.

Исторические сведения о квадратных уравнениях

Древний Вавилон

Уже во втором тысячелетии до нашей эры вавилоняне знали, как решать квадратные уравнения . Решение их в Древнем Вавилоне было тесно связано с практическими задачами, в основном такими, как измерение площади земельных участков, земельные работы, связанные с военными нуждами; наличие этих познаний также обусловлено развитием математики и астрономии вообще. Были известны способы решения как полных, так и неполных квадратных уравнений. Приведем примеры квадратных уравнений, решавшихся в Древнем Вавилоне, используя современную алгебраическую запись:

Правила решения квадратных уравнений во многом аналогичны современным, однако в вавилонских текстах не зафиксированы рассуждения, путем которых эти правила были получены.

Индия

Задачи, решаемые с помощью квадратных уравнений, встречаются в трактате по астрономии «Ариабхаттиам», написанным индийским астрономом и математиком Ариабхатой в 499 году нашей эры. Один из первых известных выводов формулы корней квадратного уравнения принадлежит индийскому ученому Брахмагупте (около 598 г.) ; Брахмагупта изложил универсальное правило решения квадратного уравнения, приведенного к каноническому виду: ; притом предполагалось, что в нем все коэффициенты, кроме могут быть отрицательными. Сформулированное ученым правило по своему существу совпадает с современным.

Корни квадратного уравнения на множестве действительных чисел

I способ. Общая формула для вычисления корней

Для нахождения корней квадратного уравнения в общем случае следует пользоваться приводимым ниже алгоритмом:

Вычислить значение дискриминант а квадратного уравнения: таковым для него называется выражение .

Условие
Число действительных корней	корней два	корень один (в некоторых контекстах говорят также о двух равных или совпадающих корнях — его, к тому же, называют корнем кратности 2)	делают вывод о том, что корней на множестве действительных чисел нет.
Формула			формулу комплексных корней смотрите ниже в соотв. разделе

Изложенный метод универсален, однако он далеко не единственный.

II способ. Корни квадратного уравнения при четном коэффициенте b

Для уравнений вида , то есть при четном , где

вместо формулы (1) для нахождения корней можно использовать более простые выражения .

Примечание: данные ниже формулы можно получить, подставив в стандартные формулы выражение b=2k и совершив при этом несложные преобразования.

Дискриминант		Корни
неприведенное	приведенное	D>0	неприведенное	приведенное
удобнее вычислять значение четверти дискриминанта: Все необходимые свойства при этом сохраняются.	.
		D=0

III способ. Решение неполных квадратных уравнений

К решению неполных квадратных уравнений следует подходить по-особому. Рассмотрим три возможных ситуации.

b=0, c=0	b=0; c≠0	b≠0; c=0
(процесс преобразования специально показан подробно, на практике можно сразу переходить к последнему равенству)	Если , то уравнение имеет два действительных корня, a если , то уравнение не имеет действительных корней.	или Такое уравнение обязательно имеет два действительных корня

IV способ. Использование частных соотношений коэффициентов

Существуют частные случаи квадратных уравнений, в которых коэффициенты находятся в соотношениях между собой, позволяющих решать их гораздо проще.

Корни квадратного уравнения, в котором сумма старшего коэффициента и свободного члена равна второму коэффициенту

Если в квадратном уравнении сумма первого коэффициента и свободного члена равна второму коэффициенту: , то его корнями являются и число, противоположное отношению свободного члена к старшему коэффициенту ().

Отсюда, прежде, чем решать какое-либо квадратное уравнение, следует проверить возможность применения к нему этой теоремы: сравнить сумму старшего коэффициента и свободного члена со вторым коэффициентом.

Корни квадратного уравнения, сумма всех коэффициентов которого равна нулю

Если в квадратном уравнении сумма всех его коэффициентов равна нулю (), то корнями такого уравнения являются и отношение свободного члена к старшему коэффициенту ().

Отсюда, прежде, чем решать уравнение стандартными методами, следует проверить применимость к нему этой теоремы: сложить все коэффициенты данного уравнения и посмотреть, не равна ли нулю эта сумма.

V способ. Разложение квадратного трехчлена на линейные множители

Если трехчлен вида удастся каким-либо образом представить в качестве произведения линейных множителей , то можно найти корни уравнения — ими будут и , действительно, ведь , а решив указанные линейные уравнения, получим вышеописанное. Отметим, что квадратный трехчлен не всегда раскладывается на линейные множители с действительными коэффициентами: это возможно, если соответствующее ему уравнение имеет действительные корни.

Рассмотрим некоторые частные случаи.

Использование формулы квадрата суммы (разности)

Если квадратный трехчлен имеет вид , то применив к нему названную формулу, мы сможем разложить его на линейные множители и, значит, найти корни:

Выделение полного квадрата суммы (разности)

Также названную формулу применяют, пользуясь методом, получившим названия «выделение полного квадрата суммы (разности)». Применительно к приведенному квадратному уравнению с введенными ранее обозначениями, это означает следующее:

1. прибавляют и отнимают одно и то же число
   .
2. применяют формулу к полученному выражению, переносят вычитаемое и свободный член в правую часть
   
   
3. извлекают из левой и правой частей уравнения квадратный корень и выражают переменную
   
   

Примечание: если вы заметили, данная формула совпадает с предлагаемой в разделе «Корни приведенного квадратного уравнения», которую, в свою очередь, можно получить из общей формулы (1) путем подстановки равенства a=1. Этот факт не просто совпадение: описанным методом, произведя, правда, некоторые дополнительные рассуждения, можно вывести и общую формулу, а также доказать свойства дискриминанта.

VI способ. Использование прямой и обратной теоремы Виета

Прямая теорема виета (см. ниже в одноименном разделе) и обратная ей теорема позволяют решать приведенные квадратные уравнения устно, не прибегая к вычислениям по формуле (1).

Согласно обратной теореме, всякая пара чисел (число) , будучи решением системы уравнений

являются корнями уравнения .

Подобрать устно числа, удовлетворяющие этим уравнениям, поможет прямая теорема. С ее помощью можно определить знаки корней, не зная сами корни. Для этого следует руководствоваться правилом:

1) если свободный член отрицателен, то корни имеют различный знак, и наибольший по модулю из корней — знак, противоположный знаку второго коэффициента уравнения;

2) если свободный член положителен, то оба корня обладают одинаковым знаком, и это — знак, противоположный знаку второго коэффициента.

VII способ. Метод «переброски»

Так называемый метод «переброски» позволяет сводить решение неприведенных и непреобразуемых к виду приведенных с целыми коэффициентами путем их деления на старший коэффициент уравнений к решению приведенных с целыми коэффициентами. Он заключается в следующем:

1) умножаем обе части на выражение:

2) вводим новую переменную :

Далее уравнение решают устно описанным выше способом, затем возвращаются к исходной переменной и находят корни уравнений и .

Геометрический смысл

Графиком квадратичной функции является парабола. Решениями (корнями) квадратного уравнения называют абсциссы точек пересечения параболы с осью абсцисс. Если парабола, описываемая квадратичной функцией, не пересекается с осью абсцисс, уравнение не имеет вещественных корней. Если парабола пересекается с осью абсцисс в одной точке (в вершине параболы), уравнение имеет один вещественный корень (также говорят, что уравнение имеет два совпадающих корня). Если парабола пересекает ось абсцисс в двух точках, уравнение имеет два вещественных корня (см. изображение справа.)

Если коэффициент положительный, ветви параболы направлены вверх и наоборот. Если коэффициент положительный (при положительном , при отрицательном наоборот), то вершина параболы лежит в левой полуплоскости и наоборот.

Графический способ решения квадратных уравнений

Помимо универсального способа, описанного выше, существует так называемый графический способ. В общем виде этот способ решения рационального уравнения вида заключается в следующем: в одной системе координат строят графики функций и и находят абсциссы общих точек этих графиков; найденные числа и будут корнями уравнения.

Есть всего пять основных способов графического решения квадратных уравнений.

Способ I

Для решения квадратного уравнения этим способом строится график функции и отыскивается абсциссы точек пересечения такого графика с осью .

Способ II

Для решения того же уравнения этим способом его преобразуют к виду и строят в одной системе координат графики квадратичной функции и линейной функции , затем находят абсциссу точек их пересечения.

Способ III

Решение этим методом подразумевает преобразование исходного уравнения к виду , используя метод выделения полного квадрата суммы (разности) и затем в . После этого строятся график функции (им является график функции , смещенный на единиц масштаба вправо или влево в зависимости от знака) и прямую , параллельную оси абсцисс. Корнями уравнения будут абсциссы точек пересечения параболы и прямой.

Способ IV

Квадратное уравнение преобразуют к виду , строят график функции (им является график функции , смещенный на единиц масштаба вверх, если этот коэффициент положителен, либо вниз если он отрицателен), и , находят абсциссы их общих точек.

Способ V

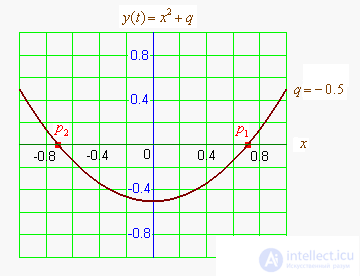
Квадратное уравнение преобразуют к особому виду:

затем

.

Совершив преобразования, строят графики линейной функции и обратной пропорциональности , отыскивают абсциссы точек пересечения этих графиков. Этот метод имеет границу применимости: если , то метод не используется.

Решение квадратных уравнений с помощью циркуля и линейки

Описанные выше методы графического решения имеют существенные недостатки: они достаточно трудоемки, при этом точность построения кривых — парабол и гипербол — низка. Указанные проблемы не присущи предлагаемому ниже методу, предполагающему относительно более точные построения циркулем и линейкой.

Чтобы произвести такое решение, нужно выполнить нижеследующую последовательность действий.

1. Построить в системе координат Oxy окружность с центром в точке , пересекающую ось y в точке C(0;1).
2. Далее возможны три случая:
   • длина радиуса окружности превышает длину перпендикуляра к оси абсцисс, опущенного из точки S: в этом случае окружность пересекает ось x в двух точках, а уравнение имеет два действительных корня, равных абсциссам этих точек;
   • радиус равен перпендикуляру: одна точка и один вещественный корень кратности 2;
   • радиус меньше перпендикуляра: корней в множестве нет.

Корни квадратного уравнения на множестве комплексных чисел

Уравнение с действительными коэффициентами

Квадратное уравнение с вещественными коэффициентами имеет ровно два комплексных корня, о чем гласит основная теорема алгебры. При этом, в зависимости от значения дискриминанта , как один, так и оба корня могут не иметь мнимой части и быть вещественными:

• при вещественных корней два, и они вычисляются по формуле

  

• при корень один (о чем также можно говорить как о двух равных или совпадающих корнях), кратности 2:

  

• при вещественных (действительных) корней нет, однако существуют два комплексных корня, выражающиеся той же формулой, что и для положительного дискриминанта. Также ее можно переписать, выразив корень из отрицательного числа в виде произведения корня с мнимой единицей:

  

Уравнение с комплексными коэффициентами

В комплексном случае квадратное уравнение решается по той же формуле (1) и указанным выше ее вариантам, но различимыми являются только два случая: нулевого дискриминанта (один двукратный корень) и ненулевого (два простых корня).

Корни приведенного квадратного уравнения

Квадратное уравнение вида в котором старший коэффициент равен единице, называют приведенным. В этом случае формула для корней (1) упрощается до

Мнемонические правила:

• Из «Радионяни»:

«Минус» напишем сначала,
Рядом с ним p пополам,
«Плюс-минус» знак радикала,
С детства знакомого нам.
Ну, а под корнем, приятель,
Сводится все к пустяку:
p пополам и в квадрате
Минус прекрасное q.

• Из «Радионяни» (другой вариант):

p, со знаком взяв обратным,
На два мы его разделим,
И от корня аккуратно
Знаком «минус-плюс» отделим.
А под корнем очень кстати
Половина p в квадрате
Минус q — и вот решенья,
То есть корни уравненья.

Теорема Виета

Формулировка

Сумма корней приведенного квадратного уравнения равна коэффициенту со знаком «минус», а произведение корней равно свободному члену

В общем случае, то есть для не приведенного квадратного уравнения :

Используя эту теорему, можно решать некоторые квадратные уравнения устно.

Разложение квадратного трехчлена на множители и теоремы, следующие из этого

Если известны оба корня квадратного трехчлена, его можно разложить по формуле

(2)

Доказательство

Для доказательства этого утверждения воспользуемся теоремой Виета. Согласно этой теореме, корни и квадратного уравнения образуют соотношения с его коэффициентами: . Подставим эти соотношения в квадратный трехчлен:

.

В случае нулевого дискриминанта это соотношение становится одним из вариантов формулы квадрата суммы или разности.

Из формулы (2) имеются два важных следствия:

Следствие 1

Если квадратный трехчлен раскладывается на линейные множители с вещественными коэффициентами, то он имеет вещественные корни.

Доказательство

Пусть . Тогда, переписав это разложение, получим:

.

Сопоставив полученное выражение с формулой (2), находим, что корнями такого трехчлена являются и . Так как коэффициенты вещественны, то и числа, противоположные их отношениям также являются элементами множества .

Следствие 2

Если квадратный трехчлен не имеет вещественных корней, то он не раскладывается на линейные множители с вещественными коэффициентами.

Доказательство

Действительно, если мы предположим противное (что такой трехчлен раскладывается на линейные множители), то, согласно следствию 1, он имеет корни в множестве , что противоречит условию, а потому наше предположение неверно, и такой трехчлен не раскладывается на линейные множители.

Уравнения, сводящиеся к квадратным

Алгебраические

Уравнение вида является уравнением, сводящимся к квадратному.

В общем случае оно решается заменой c последующим решением квадратного уравнения .

Также при решении можно обойтись без замены, решив совокупность двух уравнений:

и

Если , то уравнение принимает вид:

Такое уравнение называется биквадратным .

С помощью замены

к квадратному уравнению сводится уравнение

известное как возвратное или обобщенно-симметрическое уравнение .

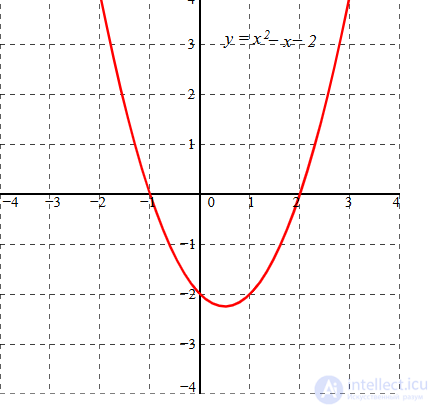
Для квадратичной функции:
f (x) = x² − x − 2 = (x + 1)(x − 2) действительной переменной x, x — координаты точки, где график пересекает ось x-ов, x = −1 и x = 2, являются решениями квадратного уравнения: x² − x − 2 = 0.

Дифференциальные

Линейное однородное дифференциальное уравнение с постоянными коэффициентами второго порядка

подстановкой сводится к характеристическому квадратному уравнению:

Если решения этого уравнения и не равны друг другу, то общее решение имеет вид:

, где и — произвольные постоянные.

Для комплексных корней можно переписать общее решение, используя формулу Эйлера:

Если решения характеристического уравнения совпадают , общее решение записывается в виде:

Уравнения такого типа часто встречаются в самых разнообразных задачах математики и физики, например, в теории колебаний или теории цепей переменного тока.

Применение решений квадратных уравнений

Решение квадратных уравнений имеет множество практических применений в различных областях. Вот несколько основных:

1. Физика и механика

• Расчет траекторий: Формулы для движения объектов, брошенных под углом или свободно падающих тел, часто включают квадратные уравнения для расчета траекторий, скорости и времени.
• Ускорение и торможение: При анализе движения с ускорением или замедлением квадратные уравнения помогают рассчитать расстояние, которое пройдет тело за определенное время.

2. Строительство и архитектура

• Оптимизация пространства: При проектировании помещений, архитекторы используют квадратные уравнения для вычисления оптимальных размеров и распределения нагрузки.
• Силы и устойчивость: Для расчета усилий на балках, арках и других элементах конструкций используются уравнения с квадратичной зависимостью, особенно в проектах мостов и зданий.

3. Экономика и бизнес

• Максимизация прибыли и минимизация затрат: В экономике квадратные уравнения применяются для анализа доходности и оптимизации затрат, например, для определения точек максимальной или минимальной прибыли.
• Анализ спроса и предложения: Для нахождения точек равновесия и анализа тенденций также могут использоваться квадратные уравнения.

4. Инженерия и технологии

• Электрические цепи и колебания: В электротехнике квадратные уравнения применяются для расчета амплитуды и частоты колебаний, особенно в цепях с индуктивностью и емкостью.
• Оптика и фокусировка: Квадратные уравнения важны для расчета фокусного расстояния в оптике, чтобы обеспечить точное изображение.

5. Финансовое моделирование

• Расчет кредита и ипотеки: При расчете платежей по кредитам и ипотеке квадратные уравнения используются для определения оптимальных сумм платежей и общей суммы процентов.
• Инвестиционные расчеты: В задачах оценки роста инвестиций и анализа доходности также применяются квадратичные зависимости для предсказания изменений.

6. Компьютерная графика и анимация

• 3D-моделирование и рендеринг: Квадратные уравнения используются для моделирования кривых поверхностей, теней и освещения.
• Физика в играх: При создании симуляций движения объектов, таких как мяч, прыгающий под разными углами, или траектории снарядов, квадратные уравнения помогают рассчитывать реалистичные движения и коллизии.

7. Астрономия и космические исследования

• Расчеты орбит: Квадратные уравнения используются для определения траекторий космических объектов, расчета орбит спутников и прогнозирования движения планет.
• Расчеты массы и гравитации: Эти уравнения важны для вычисления сил гравитационного притяжения и скорости небесных тел.

8. Решение дифференциальных уравнений

• Характеристическое уравнение: При решении линейных дифференциальных уравнений с постоянными коэффициентами часто составляется характеристическое уравнение, которое может быть квадратным. Например, для уравнений вида ay′′+by′+cy=0 характеристическое уравнение ar2+br+c=0 является квадратным. Корни этого уравнения дают решение для дифференциального уравнения.
• Колебательные системы: В задачах механики и электротехники, где рассматриваются колебательные процессы (например, в колебательном контуре или в системах с пружинами), квадратные уравнения помогают определить частоту и амплитуду колебаний. Дифференциальные уравнения второго порядка, описывающие колебания, часто приводят к квадратным характеристическим уравнениям, решая которые можно найти частоту колебаний.

---

Эти примеры показывают, что квадратные уравнения необходимы для анализа и решения задач в науке, технике, бизнесе и других практических областях, где присутствует квадратичная зависимость.

Вау!! 😲 Ты еще не читал? Это зря!

• методы решения систем линейных алгебраических уравнений ,
• кубическое уравнение ,
• линейное уравнение ,
• Решение квадратных уравнений с цепными дробями
• Линейное уравнение
• Кубическая функция
• Уравнение четвертой степени
• Основная теорема алгебры
• Уравнение пятой степени

Я что-то не договорил про квадратное уравнение, тогда сделай замечание в комментариях Надеюсь, что теперь ты понял что такое квадратное уравнение, ax² + bx + c a ≠ 0, теорема виета, уравнение второй степени, дискриминант и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА