Лекция
Привет, Вы узнаете о том , что такое статистические методы распознавания образов, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое статистические методы распознавания образов , настоятельно рекомендую прочитать все из категории Распознавание образов.
Говоря о статистических методах распознавания, мы предполагаем установление связи между отнесением объекта к тому или иному классу (образу) и вероятностью ошибки при решении этой задачи. В ряде случаев это сводится к определению апостериорной вероятности принадлежности объекта образу  при условии, что признаки этого объекта приняли значения
при условии, что признаки этого объекта приняли значения  . Начнем с байесовского решающего правила. По формуле Байеса
. Начнем с байесовского решающего правила. По формуле Байеса

Здесь  – априорная вероятность предъявления к распознаванию объекта
– априорная вероятность предъявления к распознаванию объекта  -го образа:
-го образа:
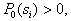
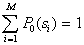 .
.
Для каждого 
 ,
,
при признаках с непрерывной шкалой измерений
 ,
,
при признаках с дискретной шкалой измерений
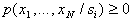 .
.
При непрерывных значениях признаков 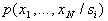 представляет из себя функцию плотности вероятностей, при дискретных – распределение вероятностей.
представляет из себя функцию плотности вероятностей, при дискретных – распределение вероятностей.
Распределения, описывающие разные классы, как правило, "пересекаются", то есть имеются такие значения признаков  , при которых
, при которых
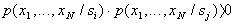 .
.
В таких случаях ошибки распознавания неизбежны. Естественно, неинтересны случаи, когда эти классы (образы) в выбранной системе признаков 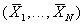 неразличимы (при равных априорных вероятностях решения можно выбирать случайным отнесением объекта к одному из классов равновероятным образом).
неразличимы (при равных априорных вероятностях решения можно выбирать случайным отнесением объекта к одному из классов равновероятным образом).
В общем случае нужно стремиться выбрать решающие правила так, чтобы минимизировать риск потерь при распознавании.
Риск потерь определяется двумя компонентами: вероятностью ошибок распознавания и величиной "штрафа" за эти ошибки (потерями). Матрица ошибок распознавания:
 ,
,
где  – вероятность правильного распознавания;
– вероятность правильного распознавания;
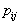 – вероятность ошибочного отнесения объекта
– вероятность ошибочного отнесения объекта  -го образа к
-го образа к 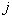 -му (
-му ( ).
).
Матрица потерь

 ,
,
где  – "премия" за правильное распознавание;
– "премия" за правильное распознавание;
 – "штраф" за ошибочное отнесение объекта
– "штраф" за ошибочное отнесение объекта  -го образа к
-го образа к 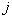 -му (
-му ( ).
).
Необходимо построить решающее правило так, чтобы обеспечить минимум математического ожидания потерь (минимум среднего риска). Такое правило называется байесовским.
Разобьем признаковое пространство  на
на  непересекающихся областей
непересекающихся областей 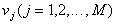 , каждая из которых соответствует определенному образу.
, каждая из которых соответствует определенному образу.
Средний риск при попадании реализаций  -го образа в области других образов равен
-го образа в области других образов равен
 ,
,  .
.
Здесь предполагается, что все компоненты 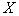 имеют непрерывную шкалу измерений (в данном случае это непринципиально).
имеют непрерывную шкалу измерений (в данном случае это непринципиально).
Величину 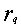 можно назвать условным средним риском (при условии, что совершена ошибка при распознавании объекта
можно назвать условным средним риском (при условии, что совершена ошибка при распознавании объекта 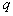 -го образа). Об этом говорит сайт https://intellect.icu . Общий (безусловный) средний риск определяется величиной
-го образа). Об этом говорит сайт https://intellect.icu . Общий (безусловный) средний риск определяется величиной 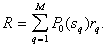
Решающие правила (способы разбиения 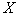 на
на 
 ) образуют множество
) образуют множество 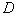 . Наилучшим (байесовским) решающим правилом является то, которое обеспечивает минимальный средний риск
. Наилучшим (байесовским) решающим правилом является то, которое обеспечивает минимальный средний риск 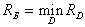 , где
, где  – средний риск при применении одного из решающих правил, входящих в
– средний риск при применении одного из решающих правил, входящих в  .
.
Рассмотрим упрощенный случай. Пусть 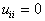 , а
, а 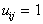 (
( ). В таком случае байесовское решающее правило обеспечивает минимум вероятности (среднего количества) ошибок распознавания. Пусть
). В таком случае байесовское решающее правило обеспечивает минимум вероятности (среднего количества) ошибок распознавания. Пусть  . Вероятность ошибки первого рода (объект 1-го образа отнесен ко второму образу)
. Вероятность ошибки первого рода (объект 1-го образа отнесен ко второму образу)
 ,
,
где  – вероятность ошибки второго рода
– вероятность ошибки второго рода
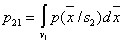 .
.
Средние ошибки
 .
.
Так как  , то
, то 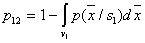 и
и  . Ясно, что минимум
. Ясно, что минимум 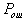 будет иметь минимум в том случае, если подынтегральное выражение в области
будет иметь минимум в том случае, если подынтегральное выражение в области 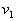 будет строго отрицательным, то есть в
будет строго отрицательным, то есть в 
 . В области
. В области  должно выполняться противоположное неравенство. Это и есть байесовское решающее правило для рассматриваемого случая. Оно может быть записано иначе:
должно выполняться противоположное неравенство. Это и есть байесовское решающее правило для рассматриваемого случая. Оно может быть записано иначе: 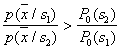 ; величина
; величина 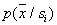 , рассматриваемая как функция от
, рассматриваемая как функция от 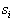 , называется правдоподобием
, называется правдоподобием  при данном
при данном  , а
, а  – отношением правдоподобия. Таким образом, байесовское решающее правило можно сформулировать как рекомендацию выбирать решение
– отношением правдоподобия. Таким образом, байесовское решающее правило можно сформулировать как рекомендацию выбирать решение  в случае, если отношение правдоподобия превышает определенное пороговое значение, не зависящее от наблюдаемого
в случае, если отношение правдоподобия превышает определенное пороговое значение, не зависящее от наблюдаемого  .
.
Без специального рассмотрения укажем, что если число распознаваемых классов больше двух (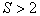 ), решение в пользу класса (образа)
), решение в пользу класса (образа)  принимается в области
принимается в области 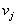 , в которой для всех
, в которой для всех 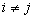
 .
.
Иногда при невысокой точности оценки апостериорной вероятности (малых объемах обучающей выборки) используют так называемые рандомизированные решающие правила. Они состоят в том, что неизвестный объект относят к тому или иному образу не по максимуму апостериорной вероятности, а случайным образом, в соответствии с апостериорными вероятностями этих образов  . Реализовать это можно, например, способом, изображенным на рис. 18.
. Реализовать это можно, например, способом, изображенным на рис. 18.
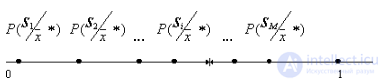
Рис. 18. Иллюстрация рандомизированного решающего правила
После вычисления апостериорных вероятностей принадлежности неизвестного объекта с параметрами  каждому из образов
каждому из образов 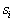 ,
,  , отрезок прямой длиной единица разбивают на
, отрезок прямой длиной единица разбивают на  интервалов с длинами, численно равными
интервалов с длинами, численно равными  , и каждому интервалу ставят в соответствие этот образ. Затем с помощью датчика случайных (псевдослучайных) чисел, равномерно распределенных на
, и каждому интервалу ставят в соответствие этот образ. Затем с помощью датчика случайных (псевдослучайных) чисел, равномерно распределенных на 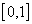 , генерируют число, определяют интервал, в который оно попало, и относят распознаваемый объект к тому образу, которому соответствует данный интервал.
, генерируют число, определяют интервал, в который оно попало, и относят распознаваемый объект к тому образу, которому соответствует данный интервал.
Понятно, что такое решающее правило не может быть лучше байесовского, но при больших значениях отношения правдоподобия ненамного ему уступает, а в реализации может оказаться достаточно простым (например, метод ближайшего соседа, о чем речь пойдет позже).
Байесовское решающее правило реализуется в компьютерах в основном двумя способами.
1. Прямое вычисление апостериорных вероятностей
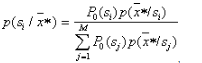 ,
,
где 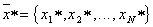 – вектор значений параметров распознаваемого объекта и выбор максимума. Решение принимается в пользу того образа, для которого
– вектор значений параметров распознаваемого объекта и выбор максимума. Решение принимается в пользу того образа, для которого  максимально. Иными словами, байесовское решающее правило реализуется решением задачи
максимально. Иными словами, байесовское решающее правило реализуется решением задачи  .
.
Если пойти на дальнейшее обобщение и допустить наличие матрицы потерь общего вида, то условный риск можно определить по формуле 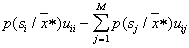 ,
,  . Здесь первый член определяет "поощрение" за правильное распознавание, а второй – "наказание" за ошибку. Байесовское решающее правило в данном случае состоит в решении задачи
. Здесь первый член определяет "поощрение" за правильное распознавание, а второй – "наказание" за ошибку. Байесовское решающее правило в данном случае состоит в решении задачи

2. "Топографическое" определение области  , в которую попал вектор
, в которую попал вектор  значений признаков, описывающих распознаваемый объект.
значений признаков, описывающих распознаваемый объект.
Такой подход используют в тех случаях, когда описание областей  достаточно компактно, а процедура определения области, в которую попал
достаточно компактно, а процедура определения области, в которую попал 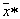 , проста. Иными словами, данный подход естественно использовать, когда в вычислительном отношении он эффективнее (проще), чем прямое вычисление апостериорных вероятностей.
, проста. Иными словами, данный подход естественно использовать, когда в вычислительном отношении он эффективнее (проще), чем прямое вычисление апостериорных вероятностей.

Рис. 19. Байесовское решающее правило
для нормально распределенных признаков
с равными ковариационными матрицами
Так, например (доказательство приводить не будем), если классов два, их априорные вероятности одинаковы,  и
и 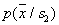 – нормальные распределения с одинаковыми ковариационными матрицами (отличаются только векторами средних), то байесовская разделяющая граница – гиперплоскость. Запоминается она значениями коэффициентов линейного уравнения. При распознавании какого-либо объекта в уравнение подставляют значения признаков
– нормальные распределения с одинаковыми ковариационными матрицами (отличаются только векторами средних), то байесовская разделяющая граница – гиперплоскость. Запоминается она значениями коэффициентов линейного уравнения. При распознавании какого-либо объекта в уравнение подставляют значения признаков  этого объекта и по знаку (плюс или минус) получаемого решения относят объект к
этого объекта и по знаку (плюс или минус) получаемого решения относят объект к  или
или  (рис. 19).
(рис. 19).
Если у классов  и
и  ковариационные матрицы
ковариационные матрицы  и
и  не только одинаковы, но и диагональны, то байесовским решением является отнесение объекта к тому классу, евклидово расстояние до эталона которого минимально (рис. 20).
не только одинаковы, но и диагональны, то байесовским решением является отнесение объекта к тому классу, евклидово расстояние до эталона которого минимально (рис. 20).
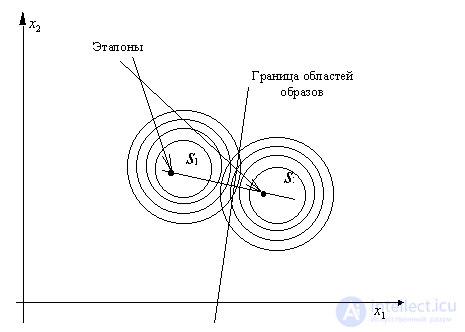
Рис. 20. Байесовское решающее правило для нормально распределенных признаков с равными диагональными ковариационными матрицами (элементы диагоналей одинаковы)
Таким образом, мы убеждаемся в том, что некоторые решающие правила, ранее рассмотренные нами как эмпирические (детерминированные, эвристические), имеют вполне четкую статистическую трактовку. Более того, в ряде конкретных случаев они являются статистически оптимальными. Список подобных примеров мы продолжим при дальнейшем рассмотрении статистических методов распознавания.
Теперь перейдем к методам оценки распределений значений признаков классов. Знание  является наиболее универсальной информацией для решения задач распознавания статистическими методами. Эту информацию можно получить двояким образом:
является наиболее универсальной информацией для решения задач распознавания статистическими методами. Эту информацию можно получить двояким образом:
заранее определить (оценить) 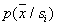 для всех
для всех 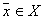 и
и  ;
;
определять 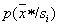 при каждом акте распознавания конкретного объекта, признаки которого имеют значения
при каждом акте распознавания конкретного объекта, признаки которого имеют значения 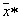 .
.
Каждый из этих подходов имеет свои преимущества и недостатки, зависящие от числа признаков, объема обучающей выборки, наличия априорной информации и т.п.
Начнем с локального варианта (определения 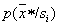 в окрестности распознаваемого объекта).
в окрестности распознаваемого объекта).
распознавание
Представленные результаты и исследования подтверждают, что применение искусственного интеллекта в области статистические методы распознавания образов имеет потенциал для революции в различных связанных с данной темой сферах. Надеюсь, что теперь ты понял что такое статистические методы распознавания образов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Распознавание образов
Из статьи мы узнали кратко, но содержательно про статистические методы распознавания образов
Комментарии
Оставить комментарий
Распознавание образов
Термины: Распознавание образов