Кластерный анализ в распознавании образов

Привет, Вы узнаете о том , что такое кластерный анализ в распознавании образов, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое кластерный анализ в распознавании образов , настоятельно рекомендую прочитать все из категории Распознавание образов.

Как уже ранее отмечалось, кластерный анализ (самообучение, обучение без учителя, таксономия) применяется при автоматическом формировании перечня образов по обучающей выборке. Все объекты этой выборки предъявляются системе без указания, какому образу они принадлежат. Подобного рода задачи решает, например, человек в процессе естественно-научного познания окружающего мира (классификации растений, животных). Этот опыт целесообразно использовать при создании соответствующих алгоритмов.

В основе кластерного анализа лежит гипотеза компактности. Предполагается, что обучающая выборка в признаковом пространстве состоит из набора сгустков (подобно галактикам во Вселенной). Задача системы – выявить и формализованно описать эти сгустки. Геометрическая интерпретация гипотезы компактности состоит в следующем.

Объекты, относящиеся к одному таксону, расположены близко друг к другу по сравнению с объектами, относящимися к разным таксонам. "Близость" можно понимать шире, чем при геометрической интерпретации. Например, закономерность, описывающая взаимосвязь объектов одного таксона, отличается от таковой в других таксонах, как это имеет место в лингвистических методах.

Мы ограничимся рассмотрением геометрической интерпретации. Остановимся на алгоритме FOREL (рис. 13).

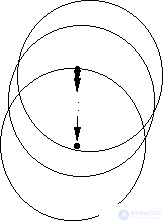
a

б

Рис. 13. Иллюстрация алгоритма FOREL: 
а – процесс перемещения формального элемента по множеству 
объектов (точек); б – иллюстрация зависимости результатов 
таксономии по алгоритму FOREL от начальной точки 
перемещения формального элемента

 Строится гиперсфера радиуса 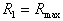, где  соответствует гиперсфере, охватывающей все объекты (точки) обучающей выборки. При этом число таксонов 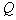 будет равно единице. Затем строится гиперсфера радиуса  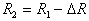с центром в произвольной точке выборки. По множеству точек, попавших внутрь гиперсферы (формального элемента), определяется среднее значение координат (эталон) и в него перемещается центр гиперсферы. Если это перемещение существенное, то заметно изменится множество точек, попавших внутрь гиперсферы, а следовательно, и их среднее значение координат. Вновь перемещаем центр гиперсферы в это новое среднее значение и т.д. до тех пор, пока гиперсфера не остановится либо зациклится. Тогда все точки, попавшие внутрь этой гиперсферы, исключаются из рассмотрения и процесс повторяется на оставшихся точках. Это продолжается до тех пор, пока не будут исчерпаны все точки. Результат таксономии: набор гиперсфер (формальных элементов) радиуса  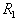с центрами, определенными в результате вышеописанной процедуры. Назовем это циклом с формальными элементами радиуса .

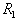В следующем цикле используются гиперсферы радиуса 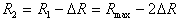. Здесь появляется параметр 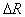, определяемый исследователем чаще всего подбором в поисках компромисса: увеличение  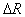ведет к росту скорости сходимости вычислительной процедуры, но при этом возрастает риск потери тонкостей таксономической структуры множества точек (объектов). Естественно ожидать, что с уменьшением радиуса гиперсфер количество выделенных таксонов будет увеличиваться. Об этом говорит сайт https://intellect.icu . Если в признаковом пространстве обучающая выборка состоит из  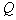компактных сгустков, далеко отстоящих друг от друга, то начиная с некоторого радиуса  несколько циклов с радиусами формальных элементов 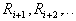 будут завершаться при одинаковом числе  таксонов. Наличие такой "полочки" в последовательности циклов разумно связывать с объективным существованием 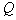 сгустков, которым в соответствие ставят таксоны. Наличие нескольких "полочек" может свидетельствовать об иерархии таксонов. На рис. 14 представлено множество точек, имеющих двухуровневую таксономическую структуру.

При всей своей наглядности и интерпретируемости результатов алгоритм FOREL обладает существенным недостатком: результаты таксономии в большинстве случаев зависят от начального выбора центра гиперсферы радиуса. Существуют различные приемы, уменьшающие эту зависимость, но радикального решения этой задачи нет. С подробностями можно ознакомиться в рекомендованной литературе [6].

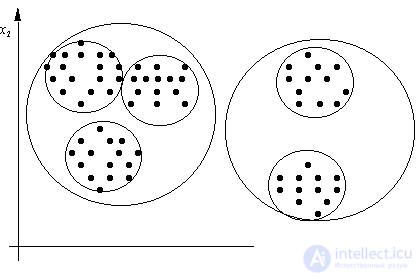
Рис. 14. Иерархическая (двухуровневая) таксономия

Примером использования человеческих критериев при решении задач таксономии служит алгоритм KRAB. Эти критерии отработаны на двухмерном признаковом пространстве в ходе таксономии, осуществляемой человеком, и применены в алгоритме, функционирующем с объектами произвольной размерности.

 Факторы, выявленные при "человеческой" таксономии, можно сформулировать следующим образом:

– внутри таксонов объекты должны быть как можно ближе друг к другу (обобщенный показатель );

– таксоны должны как можно дальше отстоять друг от друга (обобщенный показатель );

– в таксонах количество объектов должно быть по возможности одинаковым, то есть их различие в разных таксонах нужно минимизировать (обобщенный показатель );

– внутри таксонов не должно быть больших скачков плотности точек, то есть количества точек на единицу объема (обобщенный показатель ).

 Если удастся удачно подобрать способы измерения  и 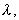 то можно добиться хорошего совпадения "человеческой" и автоматической таксономии. В алгоритме KRAB используется следующий подход.

 Все точки обучающей выборки объединяются в граф, в котором они являются вершинами. Этот граф должен иметь минимальную суммарную длину ребер, соединяющих все вершины, и не содержать петель (рис. 15). Такой граф называют КНП-графом (КНП – кратчайший незамкнутый путь).

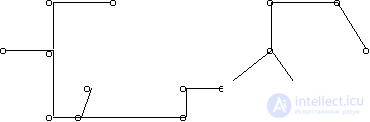
Рис. 15. Иллюстрация алгоритма KRAB

Мера близости объектов в одном таксоне – это средняя длина ребра

,

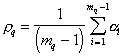где 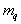 – число объектов в таксоне ,

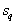 – длина -го ребра.

Усредненная по всем таксонам мера близости точек .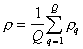

Средняя длина ребер, соединяющих таксоны, .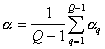

Мера локальной неоднородности определяется следующим образом.

Если длина -го ребра 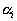, а длина кратчайшего примыкающего к нему ребра 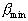, то чем меньше 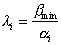, тем больше отличие в длинах ребер, тем больше оснований считать, что по ребру с длиной  пройдет граница между таксонами. Обобщающий критерий

,

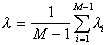где  – общее число точек в обучающей выборке.

Определим величину 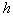 следующим образом:

.

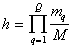 Можно показать, что при фиксированном  максимум 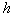 достигается при .

 Теперь можно сформировать интегрированный критерий качества таксономии

.

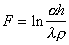 Чем больше , тем это качество выше. Таким образом, осуществляя таксономию, нужно стремиться к максимизации 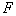. Если требуется сформировать  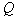таксонов, необходимо оборвать в КНП-графе  ребер, таких, чтобы критерий 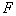 оказался максимально возможным. Это переборная задача. При большом количестве таксонов и объектов обучающей выборки число вариантов может оказаться неприемлемо большим. Желательно уменьшить вычислительные затраты. Предлагается в качестве примера следующий прием. КНП-граф строится не на множестве точек обучающей выборки, а на множестве центров гиперсфер (таксонов), найденных при помощи алгоритма FOREL. Это может резко сократить количество вершин (а следовательно и ребер) графа и сделать реализуемым полный перебор вариантов обрыва  ребер. Конечно, при этом не гарантирован глобальный максимум 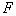, особенно если вспомнить недостатки, присущие алгоритму FOREL. Данный метод сочетания алгоритмов FOREL и KRAB назван его авторами KRAB 2.

Представленные результаты и исследования подтверждают, что применение искусственного интеллекта в области кластерный анализ в распознавании образов имеет потенциал для революции в различных связанных с данной темой сферах. Надеюсь, что теперь ты понял что такое кластерный анализ в распознавании образов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Распознавание образов