Последовательные процедуры распознавания

Привет, Вы узнаете о том , что такое последовательные процедуры распознавания, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое последовательные процедуры распознавания , настоятельно рекомендую прочитать все из категории Распознавание образов.

Если в ранее рассмотренных методах распознавания принятие решения о принадлежности объекта тому или иному образу осуществлялось сразу по всей совокупности признаков, то в данном разделе мы обсудим случай последовательного их измерения и использования.

Пусть 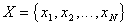. Сначала у объекта измеряется  и на основании этой информации решается вопрос об отнесении этого объекта к одному из образов. Если это можно сделать с достаточной степенью уверенности, то другие признаки не измеряются и процедура распознавания заканчивается. Если же такой уверенности нет, то измеряется признак  и решение принимается по двум признакам: и. Далее процедура либо прекращается, либо измеряется признак , и так до тех пор, пока либо будет принято решение об отнесении объекта к какому-либо образу, либо будут исчерпаны все  признаков.

Такие процедуры чрезвычайно важны в тех случаях, когда измерение каждого из признаков требует существенных затрат ресурсов (материальных, временных и пр.).

Пусть  и известны 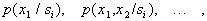  где 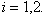 Заметим, что если известно распределение  то известны и все распределения меньшей размерности (так называемые маргинальные распределения). Например,

Пусть измерено признаков. Строим отношение правдоподобия 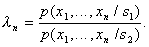 Если , то объект относим к образу , если , то к образу 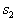. Об этом говорит сайт https://intellect.icu . Если же , то измеряется признак  и вычисляется отношение правдоподобия  и т.д.

Понятно, что пороги  и 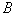 связаны с допустимыми вероятностями ошибок распознавания. Добиваясь выполнения неравенства 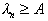, мы стремимся к тому, чтобы вероятность правильного отнесения объекта первого образа к  была в  раз больше, чем ошибочное отнесение объекта второго образа к , то есть  или . Поскольку 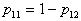, то 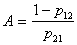 (верхний порог). Аналогичные рассуждения проводим для определения . Добиваясь выполнения неравенства , мы стремимся к тому, чтобы вероятность правильного отнесения объекта второго образа к  была в  раз больше, чем неправильного отнесения объекта первого образа к 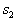, то есть

,

,

 (нижний порог).

В последовательной процедуре измерения признаков очень полезным свойством этих признаков является их статистическая независимость. Тогда 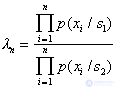 и нет необходимости в хранении (а главное – в построении) многомерных распределений. К тому же есть возможность оптимизировать порядок следования измеряемых признаков. Если их ранжировать в порядке убывания классификационной информативности (количество различительной информации) и последовательную процедуру организовать в соответствии с этой ранжировкой, можно уменьшить в среднем количество измеряемых признаков.

Мы рассмотрели случай с  (два образа). Если , то отношений правдоподобия может строиться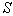, например такого вида:  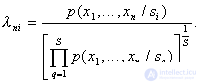Останавливающая граница (порог) для -го образа выбирается равной  Если , то 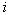-й образ отбрасывается и строится  отношений правдоподобия и порогов 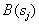. Процедура продолжается до тех пор, пока останется неотвергнутым только один образ или будут исчерпаны все  признаков. Если в последнем случае остались неотвергнутыми более чем один образ, решение принимается в пользу того из них, для которого отношение правдоподобия 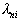 максимально.

Если образов два () и число признаков не ограничено, то последовательная процедура с вероятностью 1 заканчивается за конечное число шагов. Доказано также, что при заданных  и 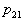 рассмотренная процедура при одинаковой информативности различных признаков даст минимум среднего числа шагов. Для  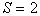последовательную процедуру ввел Вальд и назвал ее последовательным критерием отношения вероятностей (п.к.о.в.).

Для  оптимальность процедуры не доказана.

При известных априорных вероятностях можно реализовать байесовскую последовательную процедуру, а если известны затраты на измерения признаков и матрица штрафов за неверное распознавание, то последовательную процедуру можно остановить по минимуму среднего риска. Суть здесь заключена в сравнении потерь, вызванных ошибками распознавания при прекращении процедуры, и ожидаемых потерь после следующего измерения плюс затраты на это измерение. Такая задача решается методом динамического программирования, если последовательные измерения статистически независимы. Более подробные сведения об оптимизации байесовской последовательной процедуры можно почерпнуть в рекомендованной литературе [8].

Представленные результаты и исследования подтверждают, что применение искусственного интеллекта в области последовательные процедуры распознавания имеет потенциал для революции в различных связанных с данной темой сферах. Надеюсь, что теперь ты понял что такое последовательные процедуры распознавания и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Распознавание образов