Случай статистически независимых признаков

Привет, Вы узнаете о том , что такое случай статистически независимых признаков, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое случай статистически независимых признаков , настоятельно рекомендую прочитать все из категории Распознавание образов.

При статистически независимых признаках существенно упрощается решение задач распознавания. В частности, при оценивании распределений 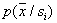 вместо многомерных плотностей вероятности достаточно оценить  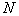одномерных плотностей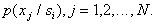 

В связи с этим рассмотренные нами примеры одномерных распределений не только носят иллюстративный характер, но могут непосредственно использоваться при решении практических задач, если есть убедительные основания считать признаки, характеризующие объекты распознавания, статистически независимыми. При этом

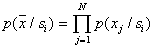
и формула Байеса, используемая для вычисления апостериорной вероятности принадлежности объекта с признаками 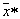 образу 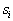, принимает вид

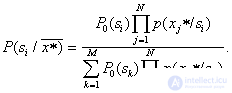
Встречаются практические приложения теории распознавания, когда признаки считают статистически независимыми без веских на то оснований, а то и зная, что на самом деле признаки (хотя бы часть из них) взаимозависимы. Это делается для упрощения процедур обучения и распознавания в ущерб "качеству" (вероятности ошибок), если этот ущерб можно признать приемлемым.

Особенно заметно упрощение процедуры распознавания по методу Байеса, если признаки принимают двоичные значения. В этом случае обучение состоит в построении следующей таблицы:

Здесь , .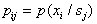

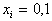Если 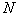 не очень велико, то отнесение неизвестного объекта к тому или иному образу настолько упрощается, что зачастую нет необходимости использовать компьютер, достаточно калькулятора, а в крайнем случае можно осуществить расчет вручную. Об этом говорит сайт https://intellect.icu . Только необходимо иметь заранее подготовленную таблицу со значениями  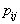(точнее, с их оценками). Если у неизвестного объекта выявлено наличие тех или иных признаков, то для каждого из образов в соответствующей строке таблицы выбираются те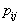, которые связаны с этими признаками, и перемножаются. Объект относят к тому классу, произведение для которого получилось максимальным. При этом, конечно, осуществляется домножение на априорные вероятности, а нормировку апостериорных вероятностей можно не осуществлять, т.к. она не влияет на результат выбора максимума по.

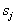Если признаки дискретны, но многозначны, то к двоичным значениям нетрудно перейти путем специальной двоичной кодировки.

Представленные результаты и исследования подтверждают, что применение искусственного интеллекта в области случай статистически независимых признаков имеет потенциал для революции в различных связанных с данной темой сферах. Надеюсь, что теперь ты понял что такое случай статистически независимых признаков и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Распознавание образов