Лекция
Привет, Вы узнаете о том , что такое параметрическое оценивание распределений, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое параметрическое оценивание распределений , настоятельно рекомендую прочитать все из категории Распознавание образов.
параметрическое оценивание распределений реализуется в тех случаях, когда известен вид распределений 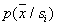 и по обучающей выборке необходимо лишь оценить значения параметров этих распределений. Априорное знание вида
и по обучающей выборке необходимо лишь оценить значения параметров этих распределений. Априорное знание вида 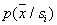 на практике встречается нечасто, однако, учитывая удобство данного подхода, иной раз делают допущение, например, о том, что
на практике встречается нечасто, однако, учитывая удобство данного подхода, иной раз делают допущение, например, о том, что  - нормальный закон. Такого рода допущения далеко не всегда имеют убедительные основания, но тем не менее используются, если результаты обучения приводят к приемлемым ошибкам распознавания.
- нормальный закон. Такого рода допущения далеко не всегда имеют убедительные основания, но тем не менее используются, если результаты обучения приводят к приемлемым ошибкам распознавания.
Итак, обучение сводится к оценке значений параметров  при заранее известном виде этих распределений. Особое место среди распределений занимает нормальный закон. Это связано с тем, что, как известно из математической статистики, если случайная величина порождена воздействием достаточно большого числа случайных факторов с произвольными законами распределения и среди этих влияний нет явно доминирующего, то интересующая нас величина имеет нормальный закон распределения. Об этом говорит сайт https://intellect.icu . Для одномерного случая
при заранее известном виде этих распределений. Особое место среди распределений занимает нормальный закон. Это связано с тем, что, как известно из математической статистики, если случайная величина порождена воздействием достаточно большого числа случайных факторов с произвольными законами распределения и среди этих влияний нет явно доминирующего, то интересующая нас величина имеет нормальный закон распределения. Об этом говорит сайт https://intellect.icu . Для одномерного случая
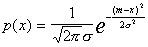
(для простоты впредь будем рассматривать одномерный случай, а заинтересовавшиеся слушатели могут обратиться к литературе, приведенной в конце конспекта лекций).
Параметрами этого распределения являются две величины:  – математическое ожидание,
– математическое ожидание,  – дисперсия. Их-то и нужно оценить по выборке. Одним из наиболее простых является метод моментов. Он применим для распределений
– дисперсия. Их-то и нужно оценить по выборке. Одним из наиболее простых является метод моментов. Он применим для распределений 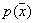 , зависящих от
, зависящих от  параметров, имеющих
параметров, имеющих 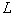 конечных первых моментов, которые могут быть выражены как явные функции
конечных первых моментов, которые могут быть выражены как явные функции  параметров
параметров . Тогда, вычислив по выборке
. Тогда, вычислив по выборке 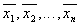
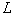 первых ее моментов и приравняв их
первых ее моментов и приравняв их 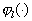 , получим систему уравнений
, получим систему уравнений
 ,
,
из которой определяются оценки  .
.
Для одномерного нормального закона
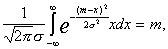
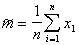 .
.
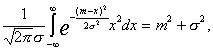
 .
.
Комментарии
Оставить комментарий
Распознавание образов
Термины: Распознавание образов