Лекция
Привет, Вы узнаете о том , что такое модели, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое модели, модель, виды моделей, принцип черного ящика, черный ящик , настоятельно рекомендую прочитать все из категории Системный анализ (системная философия, теория систем).
Понятие модели некоторого объекта возникает в связи с необходимостью изучения возможностей использования этого объекта для решения проблем, решения задач, достижения целей деятельности. Поэтому такой объект логично называть также изучаемым объектом.
модель (фр. modèle от лат. modulus «мера, аналог, образец») — система, исследование которой служит средством для получения информации о другой системе ; представление некоторого реального процесса, устройства или концепции.
Модель есть абстрактное представление реальности в какой-либо форме (например, в математической, физической, символической, графической или дескриптивной), предназначенное для представления определенных аспектов этой реальности и позволяющее получить ответы на изучаемые вопросы
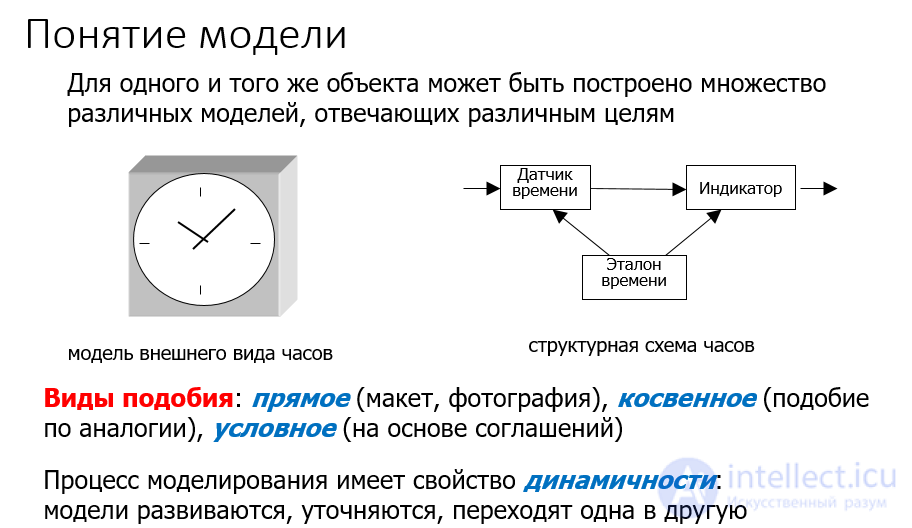
Будем исходить из следующего определения:
«модель изучаемого объекта – вспомогательный объект, дающий ответы на вопросы в отношении изучаемого объекта».
Для систем:
«модель изучаемой системы – вспомогательная система, дающая ответы на вопросы в отношении изучаемой системы».
В свою очередь, для технологии –
«модель изучаемой технологии – вспомогательная технология, дающая ответы на вопросы в отношении изучаемой технологии».
Для основной и дополнительной частей технологии –
«модель изучаемой части технологии – вспомогательная система, дающая ответы на вопросы в отношении изучаемой части технологии».
В свою очередь, для моделируемого объекта –
«модель изучаемого моделируемого объекта – вспомогательная система, дающая ответы на вопросы в отношении изучаемого моделируемого объекта».
Для частей моделируемого объекта –
«модель изучаемой части производственной систем – вспомогательная система, дающая ответы на вопросы в отношении изучаемой части моделируемого объекта».
По своей сути модель дает ответы в отношении изучаемого объекта некому субъекту, изучающему этот объект с различными целями – анализа, исследования, мониторинга и т.д. Другими словами, модель – это источник новых знаний об изучаемом объекте, необходимых для пополнения знаний изучающего о данном объекте. Тогда можно определить, что
модель – это совокупность способов и/или средств обеспечения взаимодействия между внешней средой, представленной изучаемым объектом, и внутренней средой изучающего, представляемой, в данном случае, в виде комплекса его знаний о внешней среде.
Модель изучаемого объекта можно называть также и моделирующим объектом, а изучаемый объект – моделируемым объектом.
Каждая известная модель объекта имеет один или несколько известных главных признаков, которые рассматриваются в виде аксиом в теории этой модели. Построенная на основе совокупности аксиом с помощью принятых правил вывода теория определенной модели может ответить на вопросы в отношении реального объекта, в том случае если реальный объект удовлетворяет условиям того же набора аксиом.
Другими словами, общий Принцип моделирования состоит в том, что
реальный моделируемый объект и используемая модель должны удовлетворять одному набору аксиом.
Составление единой модели какого-либо объекта в виде, позволяющем получить все ответы на вопросы в отношении изучаемого объекта, невозможно и по этой причине любые реальные объекты представляют с помощью некоторого множества известных моделей систем объектов данного класса. Каждая такая известная модель объекта позволяет ответить на некоторый комплекс вопросов в отношении построения и функционирования определенного объекта или класса объектов.
Термином моделирование обозначают как построение (создание) моделей, так и их исследование.
Одним и тем же системам могут быть сопоставлены несколько моделей разных видов.
Моделирование всегда предполагает принятие допущений той или иной степени важности. При этом должны удовлетворяться следующие требования к моделям:
Выбор модели и обеспечение точности моделирования считается одной из самых важных задач моделирования.
Точность моделей и погрешности моделирования
Погрешности моделирования вызываются как объективными причинами, связанными с упрощением реальных систем, так и субъективными, обусловленными недостатком знаний и навыков, особенностями характера того или иного человека. Погрешности можно предотвратить, компенсировать, учесть. Всегда обязательна оценка правильности получаемых результатов. В технике быструю оценку точности модели часто проводят следующими способами:
Известно, что посредством грубых измерений, использования контрольно-измерительных приборов с низкой точностью или приближенных исходных данных невозможно получить точные результаты. С другой стороны, бессмысленно вести, например, расчет с точностью до грамма, если результат потом нужно округлять (скажем, указывать в формуляре) с точностью до ста грамм, или же определять среднюю величину точнее составляющих ее значений, и т. д. Поэтому важно помнить о следующем:
В зависимости от цели изучения объекта – анализ, исследование, проектирование и т.д., используются различные способы построения моделей. Рассмотрим наиболее распространенные виды моделей.
Концептуальные, структурные и математические модели динамических систем.
Как правило, все модели являются концептуальными, структурными или математическими. Рассмотрим эти виды моделей на примере моделирования динамических систем .
Динамической системой называется упорядоченное множество взаимно связанных друг с другом элементов, существующих в реальной действительности, т.е. в пространстве и времени.
К внешней среде динамической системы относится все, не являющееся элементом данной системы.
Каждый элемент системы принято характеризовать совокупностью количественных и/или качественных признаков, изменяющихся с течением времени.
Состояние (поведение) системы в каждый фиксированный момент времени описывается однозначным выражением характеристик элементов системы.
Классическими примерами динамической системы являются система «Земля-Луна»; солнечная система, элементами которой являются Солнце, планеты и кометы; Галактика, элементами которой являются отдельные звезды, созвездия и планетные системы (в том числе и Солнечная система).
В настоящее время в теории моделирования систем различают три уровня: концептуальное моделирование, структурное моделирование; математическое моделирование.
Классическими примерами концептуальных и структурных моделей являются:
– геоцентрическая модель Птолемея, согласно которой Земля является центром всей Вселенной; Солнце, звезды и Планеты вращаются вокруг земли. Это пример модели, не удовлетворяющей общему Принципу моделирования, так как реальный моделируемый объект (Вселенная) и используемая модель (модель Птол емея) не удовлетворяют одному набору аксиом;
– гелиоцентрическая модель Коперника, согласно которой Солнце находится в центре околоземной Вселенной, планеты движутся вокруг Солнца, звезды удапены на громадные расстояния от Солнца, наблюдаемые перемещения звезд на небе не истинные, а кажущиеся за счет суточного вращения Земли вокруг своей оси;
Классическими примерами математических моделей являются:
– законы движения планет, установленные И. Кеплером в математической форме;
– математическое моделирование И. Ньютоном, Л. Эйлером механического движения твердых тел;
– закон сохранения энергии и материи М.В. Ломоносова.
В целом математические модели по степени общности и детализации делятся на следующие классы:
1) математические теории реальных процессов и ситуаций;
2) прикладные математические модели;
3) математические задачи.
Модели класса «математическая задача» содержат конкретную математическую формулировку задачи, где указаны известные и неизвестные величины и их связывающие математические соотношения, цифровые данные для известных величин, а также четко сформулировано, что требуется найти, установить или определить.
Модели класса «прикладные математические модели» также содержат ряд входных и выходных величин, связывающие их математические соотношения, при этом не указано конкретно, какие величины являются известными, а какие неизвестны. Указывается лишь в общем виде предполагаемый перечень задач, которые можно сформулировать и решить на основе данной прикладной модели.
Модели класса «математические теории реальных процессов и ситуаций» содержат достаточно полный и общий набор математических соотношений. Эти соотношения выражают реальные физические, химические, биологические, социологические и др. законы, которые позволяют на их основе разработать прикладную математическую модель для математической постановки и решения требуемого комплекса задач.
В отличие от концептуальных моделей математическая теория приводит к численному решению задач моделируемого объекта.
По способу отображения действительности различают три основных вида моделей — эвристические, натурные и математические.
Эвристические модели
Эвристические модели, как правило, представляют собой образы, рисуемые в воображении человека. Их описание ведется словами естественного языка (например, вербальная информационная модель) и, обычно, неоднозначно и субъективно. Эти модели неформализуемы, то есть не описываются формально-логическими и математическими выражениями, хотя и рождаются на основе представления реальных процессов и явлений.
Эвристическое моделирование — основное средство вырваться за рамки обыденного и устоявшегося. Но способность к такому моделированию зависит, прежде всего, от богатства фантазии человека, его опыта и эрудиции. Эвристические модели используют на начальных этапах проектирования или других видов деятельности, когда сведения о разрабатываемой системе еще скудны. На последующих этапах проектирования эти модели заменяют на более конкретные и точные.
Натурные модели
Отличительной чертой этих моделей является их подобие реальным системам (они материальны), а отличие состоит в размерах, числе и материале элементов и т. п. По принадлежности к предметной области модели подразделяют на следующие:
Физическое моделирование — основа наших знаний и средство проверки наших гипотез и результатов расчетов. Физическая модель позволяет охватить явление или процесс во всем их многообразии, наиболее адекватна и точна, но достаточно дорога, трудоемка и менее универсальна. В том или ином виде с физическими моделями работают на всех этапах проектирования;
Математические модели
Математические модели — формализуемые, то есть представляют собой совокупность взаимосвязанных математических и формально-логических выражений, как правило, отображающих реальные процессы и явления (физические, психические, социальные и т. д.). По форме представления бывают:
Например:
Построение математических моделей возможно следующими способами (более подробно — см. Математическая модель):
Математические модели более универсальны и дешевы, позволяют поставить «чистый» эксперимент (то есть в пределах точности модели исследовать влияние какого-то отдельного параметра при постоянстве других), прогнозировать развитие явления или процесса, отыскать способы управления ими. Математические модели — основа построения компьютерных моделей и применения вычислительной техники.
Результаты математического моделирования нуждаются в обязательном сопоставлении с данными физического моделирования — с целью проверки получаемых данных и для уточнения самой модели. С другой стороны, любая формула — это разновидность модели и, следовательно, не является абсолютной истиной, а всего лишь этап на пути ее познания.
Промежуточные виды моделей
К промежуточным видам моделей можно отнести:
Трехмерная компьютерная модель
Существует и другие виды «пограничных» моделей, например, экономико-математическая и т. д.
Выбор типа модели зависит от объема и характера исходной информации о рассматриваемом устройстве и возможностей инженера, исследователя. По возрастанию степени соответствия реальности модели можно расположить в следующий ряд: эвристические (образные) — математические — натурные (экспериментальные).
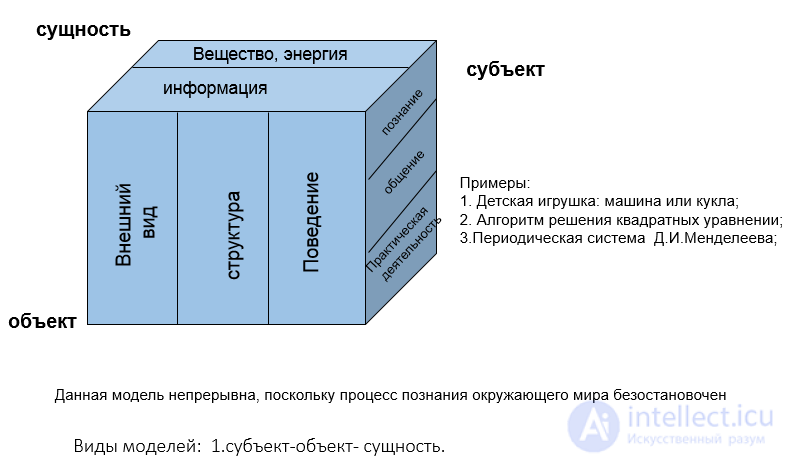
Рис Виды моделей: 1.субъект-объект- сущность.

Виды моделей: 2.субъект-объект- степень формализации.
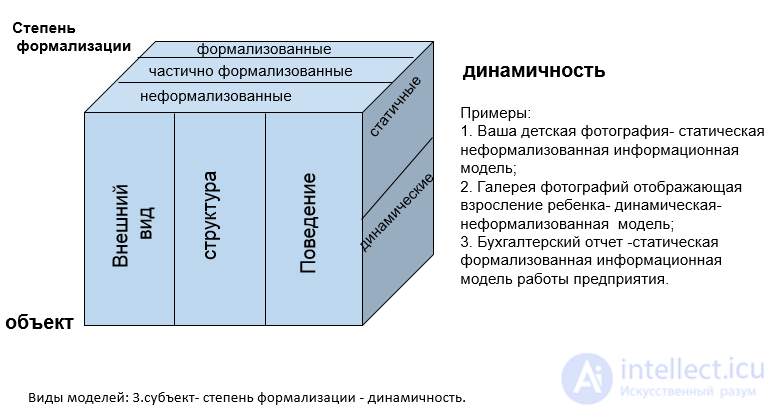
Рис Виды моделей: 3.субъект- степень формализации - динамичность.
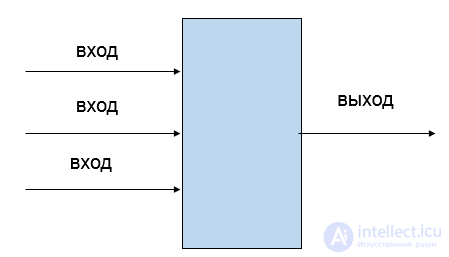
•Изменение динамической системы называют эволюцией или функционированием.
« черный ящик » динамическая система у которой явно прослеживаются входящие сигналы и моделируется выходящий сигнал. При этом внутренние строение системы нас не интересует
Примеры применения принципа черного ящика-

M(n+1)=M(n)+r*M(n)
r- коэффициент прироста за 1 год;
М(n)-количество живых объектов по истечении времени n;
М(n+1)-количество живых объектов по истечении времени n+1;
Если действия окружающей среды сказываются только на скорости прироста, то живые организмы размножаются в геометрической прогрессии.
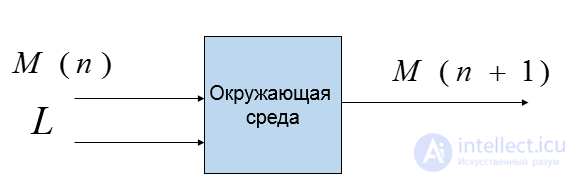
M(n+1)=M(n)+a*M(n)*(L-M(n))
a- коэффициент пропорциональности вычисляемый по формуле
a=k/(L-M(n));
L-предельное значение массы живых организмов;
М(n)-количество живых объектов по истечении времени n;
М(n+1)-количество живых объектов по истечении времени n+1;
Количество параметров, характеризующих поведение не только реальной системы, но и ее модели, очень велико. Для упрощения процесса изучения реальных систем выделяют четыре уровня их моделей, различающиеся количеством и степенью важности учитываемых свойств и параметров. Это — функциональная, принципиальная, структурная и параметрическая модели.
Функциональная модель предназначена для изучения особенностей работы (функционирования) системы и ее назначения во взаимосвязи с внутренними и внешними элементами.
Функция — самая существенная характеристика любой системы, отражает ее предназначение, то, для чего она нужна. Подобные модели оперируют, прежде всего, с функциональными параметрами. Графическим представлением этих моделей служат блок-схемы. Они отображают порядок действий, направленных на достижение заданных целей (т. н. 'функциональная схема'). Функциональной моделью является абстрактная модель.
Модель принципа действия (принципиальная модель, концептуальная модель) характеризует самые существенные (принципиальные) связи и свойства реальной системы. Это — основополагающие физические, биологические, химические, социальные и тому подобные явления, обеспечивающие функционирование системы, или любые другие принципиальные положения, на которых базируется планируемая деятельность или исследуемый процесс. Стремятся к тому, чтобы количество учитываемых свойств и характеризующих их параметров было небольшим (оставляют наиболее важные), а обозримость модели — максимальной, так чтобы трудоемкость работы с моделью не отвлекала внимание от сущности исследуемых явлений. Как правило, описывающие подобные модели параметры — функциональные, а также физические характеристики процессов и явлений. Принципиальные исходные положения (методы, способы, направления и так далее) лежат в основе любой деятельности или работы.
Так, принцип действия технической системы — это последовательность выполнения определенных действий, базирующихся на определенных физических явлениях (эффектах), которые обеспечивают требуемое функционирование этой системы.
Примеры моделей принципа действия: фундаментальные и прикладные науки (например, принцип построения модели, исходные принципы решения задачи), общественная жизнь (например, принципы отбора кандидатов, оказания помощи), экономика (например, принципы налогообложения, исчисления прибыли), культура (например, художественные принципы).
Работа с моделями принципа действия позволяет определить перспективные направления разработки (например, механика или электротехника) и требования к возможным материалам (твердые или жидкие, металлические или неметаллические, магнитные или немагнитные и так далее).
Правильный выбор принципиальных основ функционирования предопределяет жизнеспособность и эффективность разрабатываемого решения. Так, сколько бы ни совершенствовали конструкцию самолета с винтомоторным двигателем, он никогда не разовьет сверхзвуковую скорость, не говоря уже о полетах на больших высотах. Только использование другого физического принципа, например, реактивного движения и созданного на его основе реактивного двигателя, позволит преодолеть звуковой барьер.
Графическим представлением моделей принципа действия служат блок-схема, функциональная схема, принципиальная схема.
Например, для технических моделей эти схемы отражают процесс преобразования вещества, как материальной основы устройства, посредством определенных энергетических воздействий с целью реализации потребных функций (функционально-физическая схема). На схеме виды и направления воздействия, например, изображаются стрелками, а объекты воздействия — прямоугольниками.
Четкого определения структурной модели не существует. Так, под структурной моделью устройства могут подразумевать:
Под структурной моделью процесса обычно подразумевают характеризующую его последовательность и состав стадий и этапов работы, совокупность процедур и привлекаемых технических средств, взаимодействие участников процесса.
Например, — это могут быть упрощенное изображение звеньев механизма в виде стержней, плоских фигур (механика), прямоугольники с линиями со стрелками (теория автоматического управления, блок-схемы алгоритмов), план литературного произведения или законопроекта и т. д. Степень упрощения зависит от полноты исходных данных об исследуемом устройстве и потребной точности результатов. На практике виды структурных схем могут варьироваться от несложных небольших схем (минимальное число частей, простота форм их поверхностей) до близких к чертежу изображений (высокая степень подробности описания, сложность используемых форм поверхностей).
Возможно изображение структурной схемы в масштабе. Такую модель относят к структурно-параметрической. Ее примером служит кинематическая схема механизма, на которой размеры упрощенно изображенных звеньев (длины линий-стержней, радиусы колес-окружностей и т. д.) нанесены в масштабе, что позволяет дать численную оценку некоторым исследуемым характеристикам.
Для повышения полноты восприятия на структурных схемах в символьном (буквенном, условными знаками) виде могут указывать параметры, характеризующие свойства отображаемых систем. Исследование таких схем позволяет установить соотношения (функциональные, геометрические и т. п.) между этими параметрами, то есть представить их взаимосвязь в виде равенств f (x1, х2, …) = 0, неравенств f (x1, х2, …) > 0 и в иных выражениях.
Под параметрической моделью понимается математическая модель, позволяющая установить количественную связь между функциональными и вспомогательными параметрами системы. Графической интерпретацией такой модели в технике служит чертеж устройства или его частей с указанием численных значений параметров.
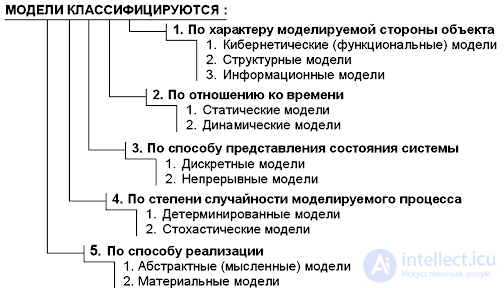
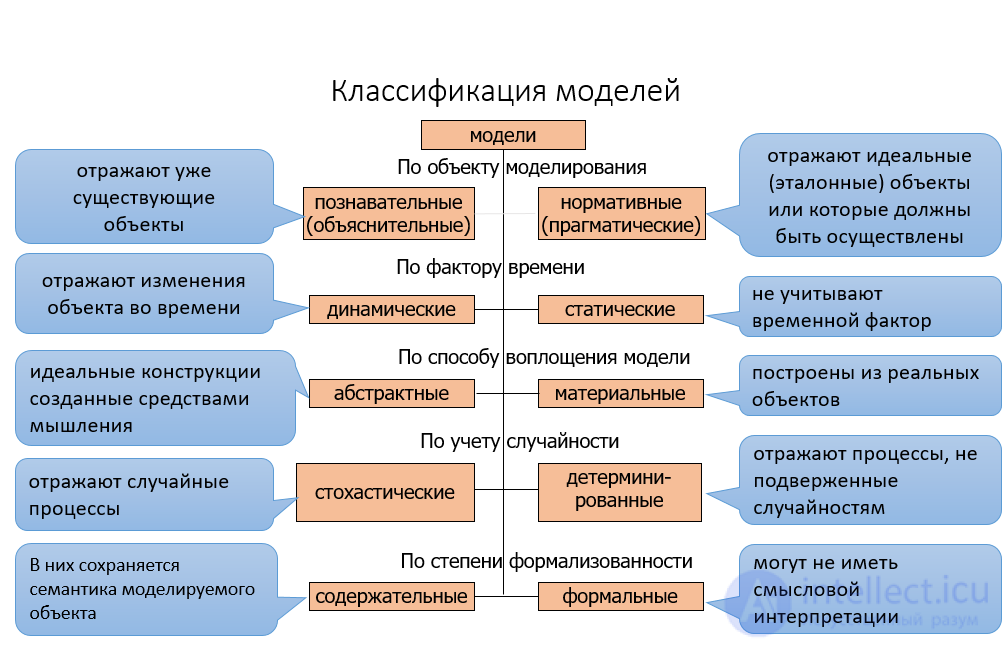
В зависимости от целей исследования выделяют следующие модели:
С целью подчеркнуть отличительную особенность модели их подразделяют на простые и сложные, однородные и неоднородные, открытые и закрытые, статические и динамические, вероятностные и детерминированные и т. д. Когда говорят, например, о техническом устройстве как простом или сложном, закрытом или открытом и т. п., в действительности подразумевают не само устройство, а возможный вид его модели, таким образом подчеркивая особенность состава или условий работы.
Знание этих особенностей облегчает процесс моделирования, так как позволяет выбрать вид модели, наилучшим образом соответствующей заданным условиям. Этот выбор основывается на выделении в системе существенных и отбрасывании второстепенных факторов и должен подтверждаться исследованиями или предшествующим опытом. Наиболее часто в процессе моделирования ориентируются на создание простой модели, что позволяет сэкономить время и средства на ее разработку. Однако повышение точности модели, как правило, связано с ростом ее сложности, так как необходимо учитывать большое число факторов и связей. Разумное сочетание простоты и потребной точности и указывает на предпочтительный вид модели.
В психологии моделирование — это исследование психических феноменов и процессов при помощи реальных (физических) или идеальных моделей. Под «моделью» при этом понимается система объектов или знаков, воспроизводящих некоторые существенные свойства системы-оригинала. Наличие отношений частичного подобия (гомоморфизм) позволяет использовать модель в качестве «заместителя» (или «представителя») изучаемой системы.
Психологическое моделирование рассматривается как создание формальной модели психического или социально-психологического феномена, то есть формализованной абстракции данного феномена, воспроизводящей основные, ключевые, — по мнению данного исследователя, — моменты. Целью такого моделирования может быть как экспериментальное изучение феномена на модели, так и использование модели при профессиональном образовании (обучении, тренировке). В этом плане различают две разновидности моделей :
Согласно К. К. Платонову (1970 г.) выделяют три вида моделей профессионала:
В современных представлениях модель специалиста включает включает следующие компоненты[12][13]:
При разработки в таком виде модели специалиста считается[14], что особое внимание следует уделять разработке качественных (в отличие от количественных) и эталонных требований к профессионалу. Модель специалиста предстает как образ профессионала, каким он должен быть — выраженный вербально (словесно) и зафиксированный в определенной нормативной документации.
Психологическая модель профессии, по С. А. Дружилову, включает три составляющие (субмодели) :
Деятельность как объект моделирования специфична уже тем, что она может быть представлена и как структура, и как процесс[19].
В моделируемых объектах изучаются модели процесса и структуры.
Процесс моделируемого объекта представляется как некоторая совокупность целесообразных элементарных преобразований ресурса – элементарных процессов производства результата моделируемого объекта. Все эти преобразования моделируются, как функции времени. Другими словами, процесс моделируемого объекта – это то, с помощью чего моделируемый объектреализуется во времени. Модели процесса – временные модели.
Структура моделируемого объекта моделируется как некоторая совокупность элементов производства (людей, машин, аппаратов, оборудования, автоматизированных рабочих мест), внутри каждого из которых локализовано протекание определенного элементарного процесса моделируемого объекта. Все эти элементы моделируемого объекта имеют «привязку» к определенному месту в пространстве (вода, воздух, земля, космическое пространство). Структура моделируемого объекта – это то, с помощью чего моделируемый объект реализуется в пространстве. Модели структуры –пространственные модели.
Для моделирования процессов и структур объектов часто используется принцип «черного ящика», согласно которому для предсказания поведения объекта не обязательно точно знать, как именно устроены его процесс и структура. Этот принцип широко применяется при моделировании таких больших систем, как производственные системы, на основе анализа характеристик информации о входных и выходных потоках и ресурсов системы.
Для моделирования используются машинные модели двух видов: аналоговые и дискретные.
Аналоговые модели – это, как правило, модели процессов в виде обыкновенных дифференциальных уравнений и уравнений в частных производных, решаемые на аналоговых и цифровых вычислительных машинах.
Дискретные модели, т.е. модели с развитой системой логических переходов и условий, описываемой с помощью аппарата дискретной математики (математическая логика и теория алгоритмов, теория языков и языковых процессоров, алгебраические системы и др.), решаются с помощью цифровых вычислительных машин.
Существуют также модели процессов систем, ориентированные на решение с помощью аналогово-цифровых комплексов, так как во многих случаях модели процессов моделируемого объекта являются непрерывно-дискретными.
Для решения задач моделирования процессов эффективными являются имитирующие модели. Для этих моделей не ставится задача наибольшего соответствия структуры модели структуре моделируемого процесса. Основная задача – наиболее достоверное воспроизведение реакции моделируемого процесса на внешние, в том числе и на входные воздействия в виде изменений характеристик преобразуемого ресурса. Подбор совокупности операторов преобразования входной информации в выходную информацию производится с помощью статистических математических методов.
Модель процесса структурируется в виде блоков в соответствии с достоверными представлениями о структуре моделируемого объекта. Каждый блок модели имитирует поведение определенной системы, являющейся подсистемой исследуемого моделируемого объекта. Имитирующие модели позволяют корректировать набор операторов преобразования в соответствии с текущим поведением моделируемой системы, создавать имитационные и деловые игры для принятия решений по проектированию, управлению, развитию производственных систем.
Процессы в производственных объектах часто моделируются с помощью «неформальных» графических моделей. Графические модели позволяют наглядно изобразить в виде схем, графиков, других простых и сложных графических конструкций частные и общие качественные и количественные характеристики моделей моделируемого объекта. Неформальные модели являются, как правило, этапом, предшествующим построению формальных математических, экономических и экономико-математических моделей моделируемого объекта.
Формальные математические модели производственных процессов могут быть дифференциальными (в форме дифференциальных уравнений), логическими (в форме уравнений математической логики), теоретико-множественными, алгебраическими (в форме алгебраических уравнений и систем), графовыми (в форме ориентированных и неориентированных графов), комбинаторными (в виде моделей размещения объектов в соответствии со специальными правилами), смешанными.
Модели производственных процессов и систем могут быть стохастическими и детерминированными, т.е. учитывающими (в первом случае) и не учитывающими (в другом случае) случайный характер изменений характеристик производственных процессов и преобразуемых системой ресурсов.
Для построения стохастических моделей процессов систем используют специальные методы моделирования[35] .
Процессы и структуры моделируемого объекта можно описывать с использованием функционального, морфологического и информационного подходов.
Функциональный подход используется для описания процесса моделируемого объекта. Модель процесса моделируемого объекта представляется в виде совокупности функций, преобразующих поступающие ресурсы в конечный результат функционирования моделируемого объекта – знание, товар, услугу, проект, программу, политику и.т.п. Конечный результат и входные ресурсы объекта представляются в виде функций времени. В каждый данный момент времени состояние моделируемого объекта описывается совокупностью информации о характеристиках входных ресурсов и выходных результатов. Функциональная модель предсказывает изменения состояния процесса моделируемого объекта во времени.
Морфологический подход предназначен для моделирования структуры моделируемого объекта, структур его частей. При этом выделяют элементы объекта и транспортно-складские связи между ними, предназначенные для обеспечения взаимодействий: информационные, энергетические, финансовые, социальные, материальные и др.
Информационный подход позволяет создать модель преобразования информационного ресурса, как для любого элемента и для части моделируемого объекта, так и для преобразования, проводимого моделируемым объектом в целом. Информационный подход позволяет создать информационную модель моделируемого объекта, дающую интегральное описание системы, независимо от ее природы и природы преобразуемых ресурсов.
На всем протяжении жизненного цикла некоторого объекта деятельности его развитие и взаимоотношения с внешней средой – предмет деятельности субъекта деятельности. При этом субъект деятельности должен обеспечивать достижение цели деятельности данного объекта (как собственной, так и миссионерской). Во-первых, это достижение миссионерской цели производства в интересах внешней среды. И, во-вторых, как известно из предыдущего изложения, имеется и собственная цель выживания, сохранения и развития объекта. К модели субъекта деятельности, которая существенно видоизменяется в течение жизненного цикла объекта деятельности, с позиций системной технологии предъявляются определенные требования.
На начальных фазах концептуальной стадии создаваемого объекта субъект деятельности выполняет по отношению к нему аналитические и исследовательские функции. Эти функции связаны с анализом потребностей и возможностей внешней среды в создании данного объекта. Субъект деятельности может представлять собой аналитическую группу, исследовательский коллектив. На последующих фазах концептуальной стадии, если принято решение о создании данного объекта, субъект деятельности выполняет разработку проекта создаваемого объекта. Модель субъекта деятельности дополняется моделью проектного коллектива и группы управления проектом. Функции субъекта деятельности создаваемого объекта на этой стадии заключаются в согласовании проекта с представителями внешней среды по вопросам экологии, экономики, социологии и др., а также в составлении планов реализации проекта создаваемого объекта.
На стадии физической реализации проекта объекта деятельности задачи субъекта деятельности связаны с реализацией создаваемого объекта в пространстве и во времени (структура и процесс). Здесь исследовательские и проектные функции субъекта деятельности связаны только с необходимостью корректировки проекта по ходу реализации функционирующего объекта. На этой стадии нарастают функции управления объектом, в том числе управления развитием объекта. Появляются новые функции субъекта деятельности, связанные с подготовкой проекта нового объекта, который сменит рассматриваемый объект при его моральном устаревании и выводе из обращения.
На постфизической стадии функции субъекта деятельности по отношению к объекту сводятся к сохранению информации о нем на бумажных и компьютерных носителях и в форме образцов; субъект деятельности на данной стадии представляет собой архив, музей или банк данных.
Можно сказать, что модель субъекта деятельности содержит такие подсистемы, как «аналитик», «исследователь», «проектировщик», «эксперт», «лицензиар», «управляющий производством», «система развития», «контролер», «архивариус», которые переживают разные стадии своих жизненных циклов в соответствии с задачами, которые выполняет субъект деятельности по отношению к конкретному объекту деятельности.
? Проект. Проект — это наиболее полная модель некоторого моделируемого объекта, пригодная для физического осуществления идеи создания и развития данного объекта, и проектировщик —существенная часть модели субъекта деятельности моделируемого объекта, которая заслуживает отдельного рассмотрения. Функции проектировщика тесно связаны с инженерингом производства.
Проект системы является наиболее важным видом модели моделируемого объекта, так как именно с помощью проекта объект переходит от идеи его создания к физической реализации, а затем и к постфизической стадии. При проектировании систем различают: макропроектирование (внешнее проектирование) и микропроектирование (внутреннее проектирование).
Макропроект можно рассматривать, как совокупность трех комплексов моделей – комплекс моделей внешней среды, комплекс моделей триады «объект-субъект-результат» проектируемого объекта, комплекс моделей его процесса и структуры. Такая совокупность описывает роль проектируемой триады «объект-субъект-результат» для внешней среды и роль внешней среды для проектируемой триады «объект-субъект-результат». Модель внешней среды – важный компонент, оказывающий существенное влияние на формирование макромодели проектируемого объекта. С позиций системной технологии внешняя среда включает все системы, которые не контролируются системой-субъектом данной триады и всеми ее подсистемами («исследователь», «проектировщик» и т.д.).
Микропроект можно рассматривать, как совокупность моделей проектируемой триады «объект-субъект-результат», а также ее подсистем, элементов, элементарных процессов, транспортно-складских взаимодействий между ними, описывающую роль элементов, элементарных процессов и взаимодействий для моделируемого объекта, а также, что не менее важно в смысле целостности объекта деятельности, роль моделируемого объекта для них.
На основе общего Принципа моделирования можно сформулировать Принцип целостности моделирования в виде:
для формирования и осуществления ц елостной деятельности совокупность «моделируемый объект и моделирующий объект» необходимо представлять одной совокупностью аксиом построения целостного объекта, справедливой также и для обоих объектов совокупности.
Тогда очевидно справедлив следующий Принцип целостности моделирования для системы:
для формирования и осуществления ц елостной системы совокупность «моделируемая система и моделирующая система» необходимо представлять одной совокупностью аксиом построения целостной системы, справедливой также и для каждой из обоих систем совокупности.
Также справедлив и следующий Принцип целостности моделирования для технологии:
для формирования и осуществления ц елостной технологии совокупность «моделируемая технология и моделирующая технология» необходимо представлять одной совокупностью аксиом построения целостной технологии, справедливой также и для каждой из обоих технологий совокупности.
В общем виде Принцип целостности моделирования можно сформулировать в следующем виде:
для формирования и осуществления ц елого совокупность «моделируемое целое и моделирующее целое» необходимо представлять одной совокупностью аксиом построения ц елостного целого, справедливой также и для каждого из обоих целых совокупности.
1) как правило, концептуальные, структурные, математические и иные модели и моделируемые ими объекты удовлетворяют одному набору аксиом. Но используемый в конкретных моделях этих трех видов набор аксиом является, как правило, подмножеством аксиом реального объекта. Образно говоря, любая модель описывает только часть реального моделируемого объекта; для достоверной модели, как правило, это ключевая часть объекта, определяющая смену его состояний при определенных начальных условиях с необходимой для практики точностью;
2) система, технология и модель имеют определения, фактически являющиеся частными видами представления целого с позиций целостного метода системной технологии. Другими словами, реальные система, технология и модель являются разновидностями частичной реализации целого. У каждой из этих разновидностей частичной реализации целого мы изучили присущие им особенные правила и условия реализации целого, которые автором были использованы при построении системной технологии;
3) в существующих моделях не ставится задача соответствия постулатам целостного целого; в связи с этим необходимо решение задачи создания целостных и целых моделей объектов моделирования для решения задач создания целостной и целой деятельности. С этой целью в данном разделе предложен Принцип целостности моделирования.
В заключение, эта статья об модели подчеркивает важность того что вы тут, расширяете ваше сознание, знания, навыки и умения. Надеюсь, что теперь ты понял что такое модели, модель, виды моделей, принцип черного ящика, черный ящик и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Системный анализ (системная философия, теория систем)
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Системный анализ (системная философия, теория систем)
Термины: Системный анализ (системная философия, теория систем)