СИСТЕМНЫЙ АНАЛИЗ ТРАНСПОРТНЫХ СЕТЕЙ

Привет, Вы узнаете о том , что такое теория графовб, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое теория графовб, кратчайший путь в сети, оптимальная дорожная сеть, задачи о размещении, алгоритм хакими , настоятельно рекомендую прочитать все из категории Системный анализ (системная философия, теория систем).

4.1. Основные понятия теории графов

Простейшие системы имеют линейную неразветвленную структуру. Более сложные
системы организуются посредством иерархических структур. Наряду с этими двумя видами организации систем распространен другой вид структуры, характеризующийся
обилием горизонтальных (одноуровневых) связей. Такие системы известны
под названием сетей. Простейшей системой является граф.

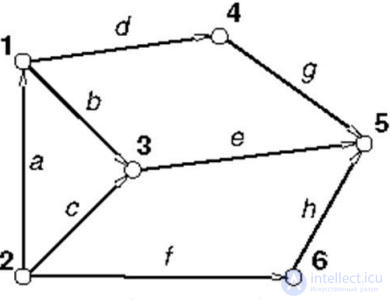
Рис. 4.1. Пример ориентированного графа
Графом G(V,E) называется система, состоящая из двух множеств: вершин (Vertices) и соединяющих их ребер (Edges). Вершина и ребро называют инцидентными, если эта вершина является одним из концов ребра. Две вершины, соединенные
ребром, называют смежными. Ребра, имеющие общую вершину, тоже называют смежными. Конечная последовательность смежных ребер называют маршрутом. Маршрут, в котором все ребра разные называется цепью. Цепь, у которой
все вершины разные, называется простой цепью. Граф G называется
связным, если любые две его вершины можно соединить хотя бы одной цепью. Цепь, у которой начальная и конечная вершины совпадают называется
циклом. Связной граф, не имеющий циклов, называется деревом. Для каждого из Граф можно построить дерево, которое содержит все его вершины. Такое дерево называют покрывающим, или покрытием графа. Если каждое ребро графа имеет направление, то граф называют ориентированным (орграфом). Направленное ребро называют дугой. Сетью называют орграф, каждая дуга которого имеет определенное числовое
значение (вес).

Граф можно задавать посредством рисунка или перечнем вершин и ребер. Однако
Самый удобный способ задания графа в плане компьютерной обработки
помощью матриц. Рассмотрим граф, представленный на рис. 4.1. Он может быть задан посредством следующей матрицы инцидентности

Каждая строчка этой матрицы соответствует вершине, а столбец – дуге. В каждом
столбце такой матрицы есть одна 1 (вход), одна –1 (выход), а остальные элементы равны нулю.

4.2. Нахождение кратчайшего пути в сети.

Моделирование структуры систем посредством графов позволяет решать многие прикладные задачи. Продемонстрируем возможности графов и сетей в сфере
оптимизации транспортных сетей Аналогичный подход можно использовать для
анализа трафика компьютерных сетей, организации строительных работ и т.д.

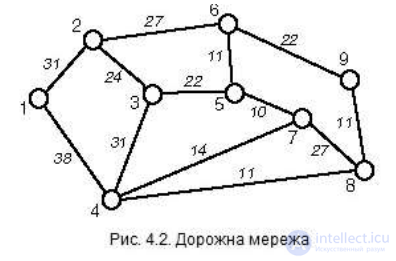
Пусть нам задана дорожная сеть, состоящая из девяти вершин (обитаемых пунктов), соединенных ребрами (дорогами) так, как это показано на Рис.2. Необходимо найти кратчайший путь от вершины 1 к вершине 8.
Одним из методов решения задачи есть алгоритм Дейкстры. Алгоритм
задачи использует три массива из n (n – количество вершин) чисел каждый.
Первый массив а содержит метки с двумя значениями: 0 (вершина еще не рассмотрена) и 1 (вершина уже рассмотрена).
Второй массив b содержит расстояния – бегущие кратчайшие расстояния от начальной вершины Vi до другой вершины Vk.
Третий массив содержит номера вершин - k-ый элемент ck является номером предпоследней вершины на бегущем кратчайшем пути с Vi до Vk. Матрица расстояний Dik задает длины ребер dik; если такого ребра нет, то dik присваивается значение очень большого числа М, равное "машинной бесконечности".

Алгоритм нахождения кратчайших путей в сети впервые был описан Дейкстроем (1959). Он состоит из трех шагов и имеет вид:
1. Инициализация. Всем элементам массива a кроме ai (начало маршрута) присвоить
Значение 0. ai := 1. Всем элементам массива b присвоить значение расстояниям из его строки матрицы Dik. Всем элементам массива c (кроме ci) присвоить значение i
(Номер начальной вершины). ci:=0.
2. Основная часть. Найти наименьшее расстояние bj среди незамеченных столбцов
(т.е. для тех j, для которых a[j]=0). Присвоить a[j]:=1 (заметить вершину).

Рассмотреть все маршруты, проходящие с вершины и через вершину j к вершине k.
Вычислить их длину bk. Если bk > bj + djk (длина нового маршрута меньше
от длины старого), то присваиваем bk:=bj+djk; ck:=j. Если bk < bj + djk ( новый
маршрут длиннее старого) – никаких изменений в k-ый столбец не вносим.

Основная часть повторяется до тех пор, пока в массиве a остается один нуль.
Процесс решения можно представить в виде следующих таблиц.

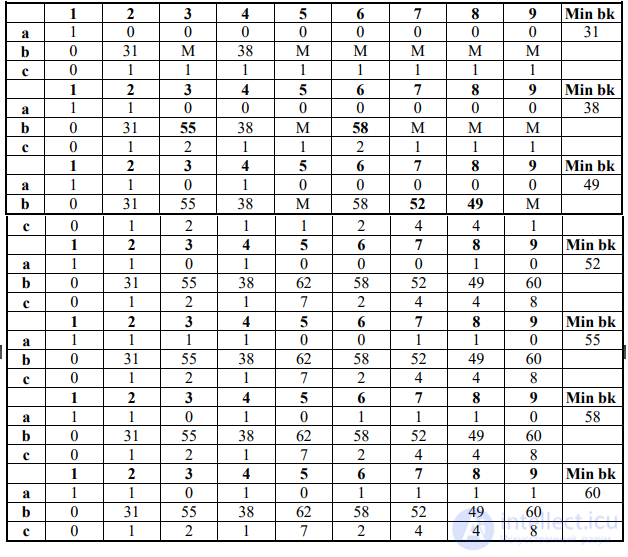
3. Вывод. Длина кратчайшего пути от вершины Vi
к вершине Vk равна bk. Теперь нужно перечислить вершины, входящие в кратчайший путь от Vi к Vk.

Для этого служит массив c. Последняя вершина – Vk, ей предшествует вершина с номером ck, перед ней будет вершина, номер которой находится в
массивные c на месте ck и т.п.
Для выполнения алгоритма нужно n раз просмотреть массив b из n элементов, то есть алгоритм Дейкстры имеет квадратичный уровень сложности.

4.3. Задача об оптимальной дорожной сети.

Есть несколько городов, которые необходимо соединить по сети дорог. Для каждой пары
городов известна проектная стоимость строительства соединяемой дороги. Задача состоит в том, чтобы построить самую дешевую из возможных дорожных сетей. Об этом говорит сайт https://intellect.icu . Аналогичные задачи можно сформулировать для сетей водо- или газопроводов.
Если рассматривать сеть дорог как граф, а стоимость строительства считать
пропорциональной длине ребра, соединяющей соответствующие вершины, то приходим
к задаче построения графа минимальной длины. Граф минимальной длины
всегда является деревом, потому что если бы граф содержал цикл, то можно было бы удалить одно из
ребер цикла не нарушив связности графа. Так что нам необходимо построить
покрывающее дерево минимальной длины. Решение задачи дает алгоритм Прима
– Краска (алчный алгоритм).

Алгоритм Прима – Краскала.

1. Выбираем еще не рассматриваемое ребро минимальной длины.
2. Присоединяем его к ранее выбранным ребрам при условии, что не образуется цикл.
3. После просмотра всех ребер образуется покрывающее дерево, которое и будет являться деревом минимальной длины.

Общая протяженность покрывающего дерева составляет 134 км.

Задача Прима.

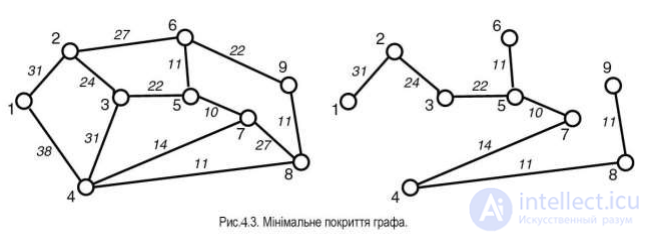
Близкой к рассмотренной задаче является задача Прима.

Есть N населенных пунктов заданных декартовыми координатами на плоскости (xi, yi).

Расстояние между пунктами определяется по формуле

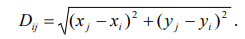( 4.1 )
Стоимость строительства дороги считается пропорциональной ее расстоянию Dij. Необходимо выстроить дорожную сеть минимальной стоимости.

Алгоритм решение выглядит следующим образом.

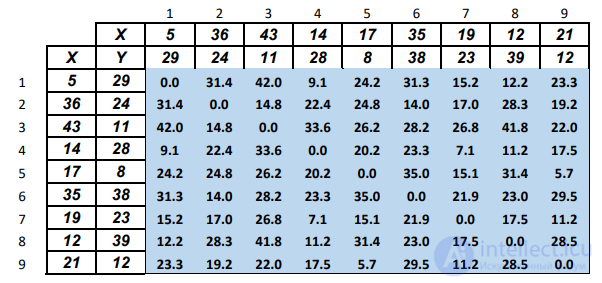
1. Строим матрицу расстояний, используя формулу (4.1).
2. Используя алгоритм Прима-Краскала строим минимальное покрывающее дерево.

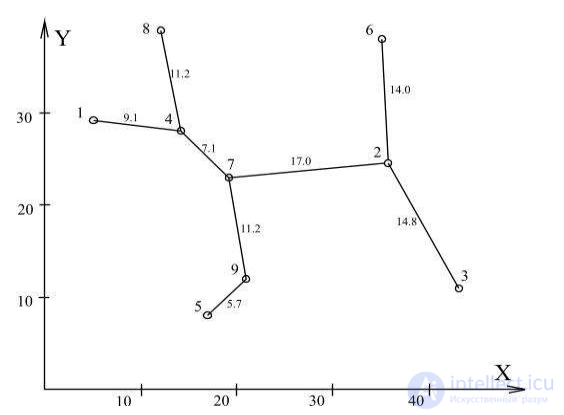
Рис.4.4. Самая короткая дорожная сеть общей протяженностью 154 км.

4.4. задачи о размещении

Важным применением системного анализа пространственных сетей являются задачи о размещении.

Решая задачу о включении нового объекта в сложившуюся систему аналогичных объектов необходимо решить вопрос перераспределения
сфер влияния объектов с минимальными затратами существующей системы.

Классическими примерами задач размещения объектов на сети являются задачи размещения школы и размещения пожарной части.

Задача размещения школы.

Задана дорожная сеть, соединяющая
девять населенных пунктов (рис.4.2). Количество учащихся в населенных пунктах известно
и составляет: 20, 40, 60, 80, 10, 30, 50, 70, 90. Необходимо оптимальным образом выбрать место для размещения новой школы.
В основу решения задачи положены рассуждения: суммарный путь,
пройденный всеми учениками по дороге в школу должен быть минимальным.

Доказаннач теорема, которая утверждает, что школа должна быть размещена в населенном пункты.
Прежде всего необходимо построить матрицу кратчайших расстояний, то есть матрицу, содержащую длины кратчайших цепей, связывающих все пункты сети друг с другом.

Для этого используется алгоритм Флойда, в основу которого положена операция треугольника:

если d[i, k] + d[k,j] < d[i,j] то d[i,j]:=d[i,k]+d[k,j].

Эта операция заменяет маршрут [i j] на маршрут [i k j] , если он короче.
Алгоритм Флойда.

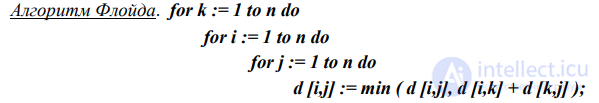
Матрица d[i,j] инициализируется следующим образом. Если вершины и и j напрямую связаны, d[i, j] равно расстоянию между вершинами, иначе d[i, j] равно
М (машинная бесконечность). После завершения работы алгоритма матрица d[i,j] содержит искомые значения длины кратчайших цепей.
В случае небольших сетей кратчайшие маршруты между вершинами можно определить вручную путем выбора вариантов.

Рассчитаем матрицу кратчайших маршрутов для сети, изображенной на рис. 4.2.

Таблица 4.1. Задача о расположении школы.

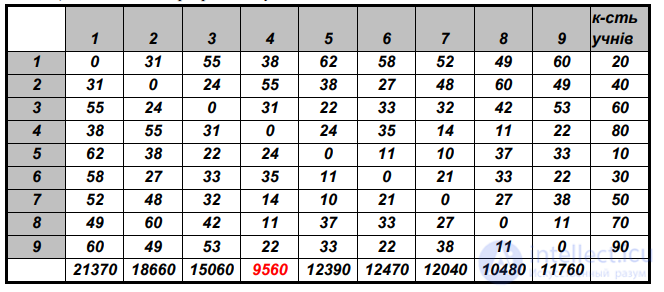
К полученной матрице присоединим еще один столбик, содержащий количество учащихся p_j в населенных пунктах.

Присоединим также дополнительную строку, которая содержит суммы вида

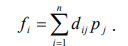( 4.2 )
Наименьшая из этих сумм (четвертый населенный пункт) и указывает оптимальное место для расположения новой школы

Поскольку в формуле (4.2) минимизируется сумма, задача о размещении школы называется минимумной.

Задача размещения пожарной части.

Необходимо разместить выезжающую пожарную часть (подразделение охраны) вызовом в один из пунктов сети (рис. 4.2).

Главной целью является: добраться до наиболее удаленного пункта за минимально возможное время.

Есть два варианта решение задачи:

а) пожарная часть в населенном пункте;

б) пожарная часть вне населенного пункта. Рассмотрим только первый вариант.

Таблица 4.2. Задача о расположении пожарной части.

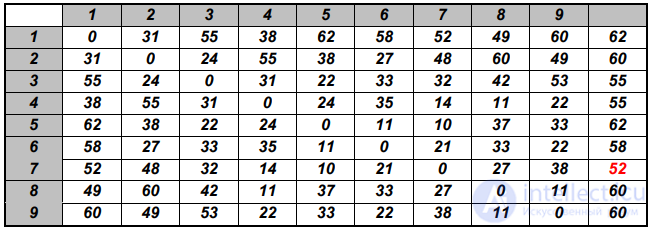
Сначала строим матрицу кратчайших маршрутов. Справа от матрицы
располагаем столбец, в котором выписываем больше всего из чисел бегущей строки
(Расстояние до наиболее удаленного пункта). Находим меньше всего из этих чисел. Это и будет лучший вариант расположения пожарной части. Для нашей
задачи это будет пункт 7. Поскольку в рассматриваемом алгоритме находится минимум среди максимальных расстояний, задача размещения пожарной части
называется минимаксной.

Алгоритм решения задачи в случае, когда пожарная часть размещается вне населенного пункта значительно сложнее.
Задача о размещении пожарной части вне населенного пункта.
Рассмотрим теперь второй вариант решения задачи: размещение пожарной части вне населенного пункта.

Сначала необходимо выяснить, какие из ребер сети наиболее перспективны для размещения пожарной части (выполнить нижнюю оценку удаленности ребер от самой дальней вершины).
Нижняя оценка удаленности ребер от самой дальней вершины.

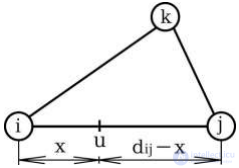
Рис.4.5. Размещение пожарной части на ребре сети

Рассмотрим ребро (ij), соединяющее вершины i и j, а также некоторую другую вершину k (рис. 4.5). Пусть x – координата (расстояние от вершины i) пожарной части u на ребре (ij).

Расстояние от вершины j до пожарной части равно d_ij –x (d_ij – длина ребра (ij)). Оптимальный маршрут от u до k определяется из условия duk = min (x+dik, dij-x+djk).

Нижняя оценка наиболее удаленного пункта определяется из условия

. (4.3)

Следовательно, мы должны просмотреть все вершины k 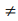i,j. Для каждой из них необходимо определить величину 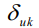и затем выбрать самую большую из них.

Это и будет нижняя оценка наиболее удаленного пункта в случае расположения пожарной части на ребре (i,j).

Рассмотренную операцию необходимо повторить для всех ребер и выбрать из всех нижних оценок наименьшую.

Это и будет ребро, на котором целесообразнее всего расположить пожарной части.
Для иллюстрации приведенных выше соображений рассмотрим пример.

В качестве сети рассмотрим ту самую сеть, о которой мы говорили в начале этого параграфа.
Используя матрицу кратчайших расстояний построенную выше, построим
таблицу нижних оценок (табл. 4.3).

Таблица 4.3
Таблица нижних оценок удаленности ребра от самой дальней вершины

Покажем, к примеру, как была получена первая оценка ребра (1,2) – число 49.
Сравним пары чисел, одно из которых принадлежит первой, а второе – второй строке матрицы кратчайших расстояний между вершинами графа, построенной нами
раньше. В рассмотрение не включаются пары, соответствующие первому и второму
столбца.

Находим

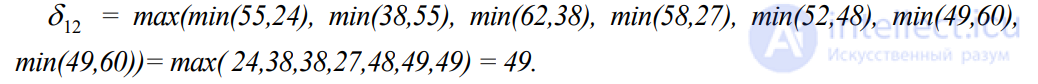
Аналогично были найдены нижние оценки всех ребер сети. Анализ таблицы показывает, что наиболее перспективными ребрами для расположения пожарной
части представляют собой ребра (1,4) и (2,6), нижняя оценка удаленности которых равна 35 км.
Теперь необходимо проводить анализ обеих ребер на предмет целесообразности размещения пожарной части.

алгоритм хакими

Завершающим этапом решения задачи о размещении пожарной части на ребре сети является определение оптимальной координаты размещения пожарной части.
части на ребре с минимальной нижней оценкой удаленности.

Решить эту задачу разрешает алгоритм Хакими.

Пусть пожарная часть u расположена на ребре (i,j) на расстоянии x от вершины i (рис. 4.6). Рассчитаем расстояния от пожарной
части ко всем вершинам сети. В нашем случае оптимальным местоположением для пожарной части выступают ребра (1,4) и (2,6). Проанализируем
второй и случай. Длина ребра составляет 27 км. Следовательно, если расстояние от вершины 2 до пожарной части составляет x км, то расстояние от вершины 6 до пожарной
части составляет 27 – х км.
Отметим dui – минимальное расстояние от пожарной части к и-ой вершине.

Тогда, например, расстояние до первой вершины будет определяться по условию
du1 = min (x+d21, d26 –x+d61 ) = min (31+ x, 58+27–x) = min(31+x, 85-x).

Учитывая, что 0 <= x <= 27, получим du1 = 31 + x.
Аналогичные соображения нужно провести и для всех остальных вершин сети.

В результате такого анализа получаем:
du2 = x;

du3 = min(24+x, 33+27-x) = 24+x;

du4 =min(55+x, 35+27-x) = 62 - x;
du5 = min (38+x, 11+27-x) = 38 – x;
du6 = 27-x;
du7 = min (48+ x, 21+27-x) = 48 – x;
du8 = min(60+x,25+27 – x) = 52 - x;
du9 = min (49+x,22+27-x) = 49 – x.
Строим графики линий du1 – du9.

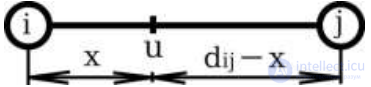
Рис. 4.6. Размещение пожарной части на ребре (i,j)

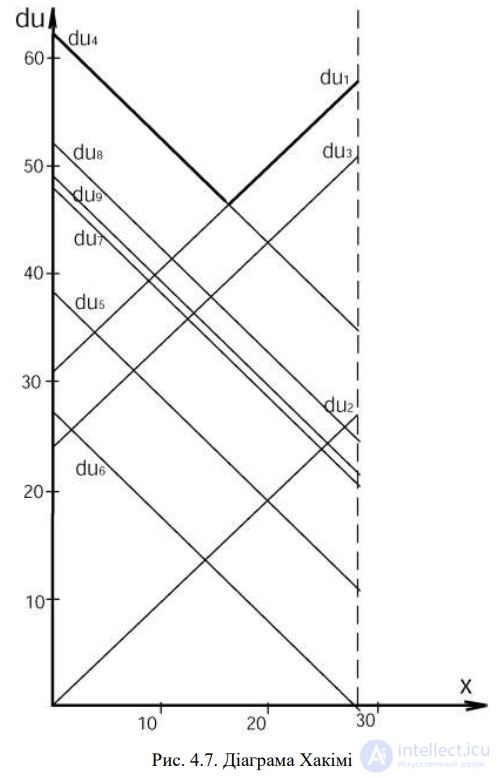
Рис. 4.7. Диаграмма Хакими

В результате получаем так называемую диаграмму
Хакими (рис. 4.7). Ее анализ показывает, что оптимальное месторасположение пожарной части является точкой пересечения линий du1 и du4. Решим уравнение для определения неизвестной координаты x: 31 + x = 62 – x.
Получаем: x = 15.5; min dui=46.5 км.
Аналогичный анализ, проведенный для ребра (1,4) дает результат min dui = 52 км.

Это означает, что данное ребро не дает выигрыша по сравнению с избранным ранее седьмым населенным пунктом.

Вывод. При размещении пожарной части в населенном пункте оптимальным вариантом станет седьмой населенный пункт. При этом расстояние до наиболее
удаленного пункта будет составлять 52 километра. При размещении пожарной части вне населенного пункта оптимальным вариантом будет ребро (2,6). Пожарную часть следует разместить в 15.5 км от 2-го пункта. При этом расстояние до наиболее отдаленного пункта (1-го или 4-го) составит 46.5 километров. Таким образом, по сравнению с первым вариантом решения, мы получили выигрыш в 5.5 километра. Размещение пожарной части на ребре (1,4) не дает выигрыша по сравнению с размещением в населенном пункте 7.

Замечания. Следует иметь в виду, что не всегда размещение пожарной части на ребре более выгодно от размещения в вершине графа. В каждом конкретном случае можно сделать вывод только после полного анализа обоих вариантов решения. В случае если несколько ребер имеют одинаковую минимальную нижнюю оценку удаленности, следует выполнять анализ по алгоритму Хакими для всех таких ребер.

Исследование, описанное в статье про теория графовб, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое теория графовб, кратчайший путь в сети, оптимальная дорожная сеть, задачи о размещении, алгоритм хакими и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Системный анализ (системная философия, теория систем)