МЕТОДЫ идентификации сложных систем

Привет, Вы узнаете о том , что такое идентификация систем, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое идентификация систем, сложные системы , настоятельно рекомендую прочитать все из категории Системный анализ (системная философия, теория систем).

идентификация систем — совокупность методов для построения математических моделей динамической системы по данным наблюдений. Математическая модель в данном контексте означает математическое описание поведения какой-либо системы или процесса в частотной или временной области, к примеру, физических процессов (движение механической системы под действием силы тяжести), экономического процесса (реакция биржевых котировок на внешние возмущения) и т. п. В настоящее время эта область теории управления хорошо изучена и находит широкое применение на практике.

7.1. Определение степени случайности системы.

Результаты деятельности экономических систем отражаются посредством временных рядов их параметров. Исследуя специфику временного ряда, мы можем
сделать выводы о характере породившей его системы. В частности, на основе исследования временных рядов делают выводы относительно размерности системы,
возможности ее прогнозирования и максимального горизонта прогнозирования, характера динамики системы (трендостойкая, случайная, реверсивная). Поэтому
обязательным этапом, предшествующим моделированию и прогнозированию экономической системы является предпрогнозный анализ временных рядов, позволяющий осуществить
частичную идентификацию системы Обязательным элементом идентификации системы есть определение характера ее динамики. Динамика системы может быть детерминирована (строго определена, предсказуема) или случайна (стохастическая, непредсказуемая). Некоторые системы на определенных временных промежутках ведут
себя детерминированы, а на других временных промежутках – случайным образом. Много
информации о характере динамики системы может дать временной ряд значений одного из показателей, характеризующих данную систему.
Рассмотрим методы определения степени случайности системы по ее временному ряду.

Рассмотрим временной ряд 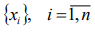в котором каждая тройка последовательных значений есть разные числа. Поворотной точкой называют значение ряда xt для которого выполняется одно из двух условий:
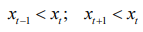или 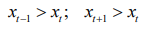;(М. Кендалл).

Обозначим минимальное число из любой тройки последовательных элементов ряда 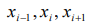символом a , промежуточное – символом b , максимальное – символом c .

При случайном размещении рассматриваемых чисел есть возможными 6 конфигураций a,b,c; a,c,b; b,a,c; b,c,a; c,a,b; c,b,a.

Если ряд есть случайным, каждая из этих конфигураций равновероятно, т.е. появления в случайном ряду составляет 1/ 6. Четыре из шести вышеперечисленных конфигураций (кроме первой и последней) соответствуют понятию «поворотной точки», введенному Кендалом. Первая и последняя конфигурация соответствуют трендоподобной динамике ряда. Таким образом, вероятность появления поворотной точки у
случайном ряду составляет 2/ 3 , вероятность трендовой триады - 1 /3 . Таким образом М. Кендалл показал, что для случайного (стохастического) ряда длиной n
среднее значение количества поворотных точек составляет

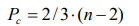
при стандартном отклонении

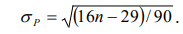
Введем следующие обозначения
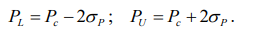(7.1)
Если фактическое количество поворотных точек Pf удовлетворяет соотношение 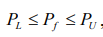, ряд считают случайным (стохастическим)

В случайном ряду в понимании Кэндела после прироста (спада) следует спад (прирост) с вероятностью 2/ 3 , а вероятность еще одного прироста (спада) составляет 1/ 3 .

Если фактическое количество поворотных точек Pf < PL это означает, что для ряду характерны трендовые участки. Такой ряд называют персистентным (трендоустойчивым).
Если Pf > PU , это означает избыточное количество колебаний, вызванное некоторым внешним фактором. Такой ряд называют антиперсистентным (реверсивным).

Идентификация временного ряда как трендостойкого или реверсивного имеет важное значение значение для выбора метода прогнозирования В первом случае используют методы экстраполяции трендовых моделей, во втором используют гармонические или авторегрессионные модели, способные воспроизвести колебания случайной. величины.

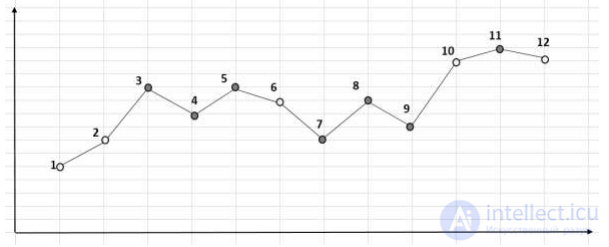
Рис. 7.1. Поворотные точки (темный фон)

7.2. Исследование автокорреляций временного ряда

Мощным инструментом исследования характера динамики системы является корреляционный анализ. Применяя корреляционный анализ к временному ряду, который
Представляет исследуемую систему, можно получить ответы на следующие вопросы: имеет ли ряд тренд? присутствует ли циклическая компонента ряда? Первый ответ описывает направленность динамики системы (возрастающая, нисходящая, стабильная),
второй ответ определяет наличие (отсутствие) колебаний.
Корреляционная зависимость между двумя разными отрезками временного ряда, смещенными на временной интервал L (лаг), называют автокорреляцией с лагом L.
Лагом называется временной промежуток между двумя отрезками временного ряда.
Введем понятие автокорреляционной функции (АКФ) 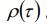для временного ряда
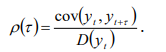. (7.2)
Здесь – коэффициент ковариации временного ряда для лага ,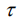

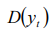– дисперсия.

Значение АКФ характеризует тесноту статистической связи между уровнями временного ряда, разделенными временными лагами.

Все значения АКФ безразмерны и удовлетворят условие 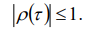. (7.3)

График АКФ отражает зависимость коэффициента автокорреляции от лага и называется коррелограммой.

При определении количества коэффициентов АКФ придерживаются правила
. (7.4)

Таким образом, последовательность коэффициентов автокорреляции первого, второго и т.д. порядков образует авттокореляционную функцию временного ряда. Анализ автокорреляционной функции и ее графика (корреллограммы) позволяет определить лаг, при котором автокорреляция наиболее высока, т.е. лаг, при котором связь между текущими и предыдущими уровнями ряда наиболее тесна.

Таким образом, с помощью анализа автокорреляционные функции и коррелограммы можно выявить особенности динамики породившей его системы. Есть несколько правил, описывающих наиболее характерные примеры коррелограмм.

1. Если наиболее высоким оказывается положительный коэффициент автокорреляции первого порядка, исследуемый ряд содержит только тренд (тенденцию к росту или убыванию).
2. Если наиболее высоким оказывается отрицательный коэффициент автокорреляции первого порядка, исследуемый ряд является реверсивным (склонным к колебаний).
3. Если наиболее высоким оказывается положительный коэффициент автокорреляции порядка T , ряд содержит циклические колебания с периодичностью T.

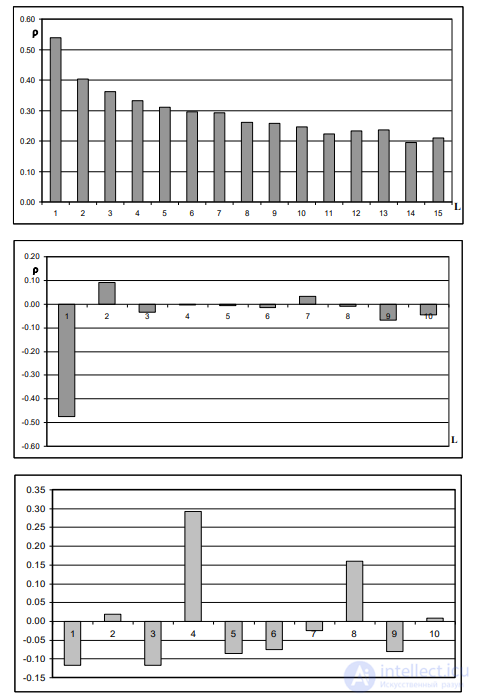
Рис.7.2. Коррелограммы ЧР.

А – ряд с длинной памятью (разлив реки Нил);

Б – ряд с короткой памятью (изменения урожайности ОП – США);

В – циклический ряд (годовые суммы осадков Ровенская область)

4. Если ни один из коэффициентов автокорреляции не является статистически значимым, можно предположить, что данный ряд не содержит тенденции и циклических колебаний и имеет структуру похожую на структуру случайного процесса.
В практических исследованиях значимым считается коэффициент автокорреляции, модуль которого превышает значение 0.2.
Рассмотрим несколько примеров коррелограмм, выполненных для реальных временных рядов.
1. АКФ содержит много важных элементов. Ряд склонен к трендам и имеет длинную память (Рис.7.2 А). Временной ряд описывает статистику величины разлива г. Нил (Египет).
2. АКФ содержит 1 значимый элемент. Об этом говорит сайт https://intellect.icu . Ряд является реверсивным и имеет короткий память (Рис.7.2 Б). Ряд урожайности озимой пшеницы (США).
3. Большинство значений АКФ незначительны, но одно из них является большим положительным –свидетельство наличие цикла с периодом 4 года (см. рис.7.2 В). Ряд годовой суммы осадков для Ровенской области.
4. Для построения коррелограммы в среде MS Excel можно использовать функцию Коррел. Например, функция “коррел($b$4 : $b$50; b5 : b51)” позволяет получить значение первого коэффициента автокорреляции
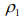для ряда длиной 56 элементов, размещенного в ячейках b4: b59; функция “коррел($b$4: $b$50; b6 : b52)” ‒ значение второго коэффициента автокорреляции 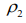и т.п.

Но, описанный метод не совсем точен. Другим методом построения коррелограммы является программа Statistica. При этом используют последовательность команд: Statistics, Advanced Linear/Nonlinear Models, Time Series/Forecasting, Arima & autocorrelation functions, Number of lags, Autocorrelations.

7.3. Описание состояния системы в фазовом пространстве

Состояние системы характеризуется совокупностью значений основных параметров
системы в данный момент времени Например, для описания экономического состояния предприятия необходимо задать числа, оценивающие валовой выпуск продукции, доход,
прибыль, рентабельность, количество работников, фонд заработной платы, производительность труда, объемы кредиторской и дебиторской задолженности, объемы инвестиций, коэффициент износа оборудования. Отметим эти параметры символами q1, q2 , q3 ,… qk .

Данные числа называют координатами состояния системы в k-размерном простори состояний или в фазовом пространстве.

При изменении состояния системы изменяются ее параметры, то есть координаты состояния являются переменными величинами, зависимыми от времени.

.
Важнейшей характеристикой фазового пространства является его размерность, то есть минимальное количество параметров, которые необходимо задать для определения
состояния системы Размерность фазового пространства, обеспечивающая однозначное представление всех возможных состояний системы, является числовой оценкой сложности
системы.
Системы, состояние которых меняется с течением времени, называют динамическими. каждому состоянию системы соответствует определенная точка фазового пространства

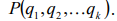
. Смену состояний динамической системы с течением времени называют процессом.

Любой процесс в экономической системе характеризуется изменением параметров, поэтому ему соответствует движение точки в фазовом пространстве. Процессу изменения состояний соответствует траектория
– линия, соединяющая соседние точки фазового пространства. Фазовая траектория отражает поведение системы под влиянием некоторых факторов. Множество всех фазовых траекторий, которым отвечают разные начальные условия, называют фазовым портрет системы. Фазовый портрет представляет собой семью непрерывных кривых. Это означает, что динамическая система может находиться в любом состоянии
только один раз.
Большинство экономических систем относятся к классу открытых нелинейных систем, называемых диссипативными. Такие системы неравновесны благодаря рассеянию ресурсов (вещество, энергия, деньги), получаемых извне. Для таких систем совокупность фазовых траекторий притягивается к некоторому конечномерному подмножеству фазового пространства, называемого аттрактором. Конечномерный аттрактор определяет свойства установившегося со временем колеблющегося процесса в системе. Колебания в экономических системах являются непериодическими и обусловлены кризисами перепроизводства, несовершенством финансовых механизмов, отсутствием эквивалентности между массой товаров и денежной массой, перепроизводством или недопроизводством продовольствия, военными и политическими конфликтами и т.д. Для некоторых динамических систем характерен странный аттрактор (рис. 7.4). Это означает, что небольшие изменения начальных условий системы могут привести к кардинальным изменениям через некоторое время. Взмах крыльев бабочки в одном месте земного шара может вызвать ураган и на другом его месте (Б. Мандельброт – эффект бабочки).

Изменение параметров состояния описывается функциями, которые непрерывны или дискретны.

Когда эти функции непрерывны, поведение динамической системы описывают с помощью системы дифференциальных уравнений:
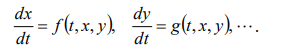. (7.5)
Различают три характерных типа поведения, или три режима, в которых может находиться динамическая система: равновесный, периодический, переходный. Равновесие системы – это способность ее сохранять свое состояние как угодно долго (как при отсутствии, так и при наличии внешних воздействий). Согласно второму закону термодинамики, при отсутствии управляющих воздействий сложная изолированная система следует
к состоянию равновесия, для которого характерны дезорганизация и хаос.
При циклическом режиме функционирования система через некоторые промежутки времени приходит в одно и то же состояние (попадает в одну точку фазового пространства). Цикличность является одним из видов стойкости. Примеры: цикличность производства сезонных продуктов, цикличность транспортных перевозок.
Процесс перехода системы из одного устойчивого состояния в другое называют переходным процессом. Изменение состояния объекта неизбежно связано с переносом вещества, энергии или финансов и не может происходить мгновенно. Скорость переходного процесса характеризует инерционность системы. Переходные процессы описываются с помощью логистической функции.

7.4. Модель Лоренца

Линейный подход не позволяет проанализировать нерегулярное поведение, которое показывают современные денежные рынки. До начала 60-х годов в нелинейных диссипативных динамических системах в стационарном режиме наблюдали только периодические и квазипериодические движения. Однако в 1963 году в динамической системе Лоренцем было найдено очень сложное движение, воспринимавшееся как хаотическое. Для свойства таковых движений ввели понятие «динамический хаос». Слово «динамический» означает, что нет источников флуктуаций. Слово «хаос» означает, что поведение системы можно прогнозировать только на очень короткий отрезок времени. Система Лоренца описывает процесс конвекции в слое жидкости между двумя горизонтальными пластинами, температура которых является постоянной, причем нижняя горячее верхней на ∆Т. Экспериментальное исследование ситуации при различных ∆Т показало, что при малых перепадах температур жидкость находится в покое и
работает только механизм теплопроводности, температура линейно падает от дна до поверхности. Затем при достижении некоторого критического перепада температур ∆Тс
состояние становится неустойчивым. Появляются шестигранные ячейки на поверхности жидкости или конвективные валы. При дальнейшем увеличении ∆Т валы начинают колебаться,
затем колебания становятся все более сложными и развивается турбулентное движение (рис. 7.3).

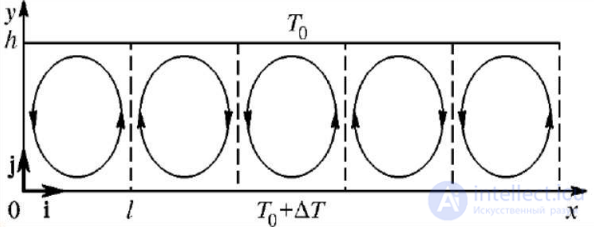
Рис. 7.3. Турбулентное движение в Лоренцовой системе.
В статье математиков Рюэля и Такенса, опубликованной в 1971 году, был введен новый математический образ динамического хаоса – удивительный аттрактор. Слово
"странный" подчеркивает два свойства аттрактора. Это, во-первых, необычность его
геометрическая структура. Размерность странного аттрактора является дробной (фрактальной). Во-вторых, странный аттрактор – это притягивающая область для траекторий из окрестных областей. При этом все траектории внутри странного аттрактора динамически неустойчивы, что выражается в сильном (экспоненциальном) расхождении.
близких в начальный момент траекторий
Математическая модель системы Лоренца имеет вид:
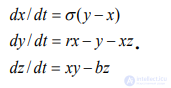. (7.6)
Здесь переменная x зависит от температуры, переменные y и z зависят от проекций скорости жидкости в горизонтальном и вертикальном направлениях. Плоская Проекция фазового портрета системы Лоренца представлена ​​на рис.7.4.

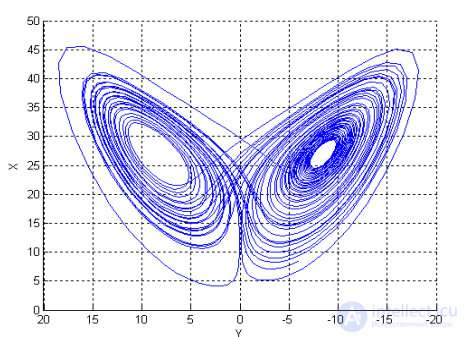
Рис. 7.4. Фазовый портрет системы Лоренца (двухмерная проекция)
Фазовый портрет представляет две группы циклических траекторий размещенных в двух разных плоскостях, расположенных под углом одна к другой. Переход траектории из одной плоскости в другую осуществляется случайно, непредсказуемо. В этом и состоит хаотичность системы. Признаком динамичности почти периодические повторения витков траектории.

7.5. Исследование систем методами хаотической динамики.

Простейшим типом динамического поведения системы является линейная динамика, характеризующаяся равномерным ростом или убыванием характеристического
показателя Более сложной является периодическая динамика, для которой характерны регулярные периоды роста и убыли показателя. Периодическая динамика есть характерно для нелинейных систем. Наиболее сложным типом динамики есть хаотическая динамика. При этом параметры системы также имеют регулярные периоды. рост и убывание, но при этом продолжительность и амплитуда колебаний являются переменными. На небольших промежутках времени системы хаотической динамики детерминированы, но горизонт прогнозирования таких систем всегда ограничен, поскольку
их поведение сильно зависит от начальных условий. Для систем хаотической динамики существует возможность моделирования с использованием дифференциальных (разностных) уравнений. Для установления типа динамики, характерной для исследуемой системы, был разработан ряд методов, большинство из которых основываются на анализе временных рядов. Большинство временных рядов являются нестационарными, поэтому на на первом этапе исследований необходимо смоделировать и изъять из ряда его тренд и циклический компонент. Полученный после этого ряд называется рядом остатков. Если тренд временного ряда носит сложный характер и его невозможно Выделить стандартными методами (элементарные функции), ряд остатков может содержать детерминированную компоненту, связанную с этим трендом. Для выделения детерминированной компоненты из ряда остатков необходимо выполнить сглаживание ряда остатков. Исследование сглаженного ряда остатков позволяет построить
фазовый портрет системы; вычислить размерность системы; оценить степень ее прогнозируемости.

Построение фазового портрета Использование методов хаотической динамики требует длины исследуемого ряда 102 – 103 элементов. В случае, если исследуемые ряды короче, используют эргодичную гипотезу и моделируют один длинный ряд рядом более коротких рядов, для которых выполняется свойство однородности (стабильность среднего значения и дисперсии). Например, при исследовании динамики урожайности зерновых и длина временных рядов составляет 60 элементов. Однако наличие циклов примерно одинаковой продолжительности позволяет рассматривать каждый ряд как несколько витков фазовой траектории. Такие ряды содержат три циклы (три витка фазовой траектории) средней продолжительностью 19 лет. Тогда, рассмотрев группу 12 областей с однородной динамикой урожайности, получим 36 витков фазовой траектории с длиной 19 лет. Согласно эргодичному принципу такой набор временных рядов можно рассматривать как аналог одного временного ряда протяженностью 684 элемента.

Вид аттрактора динамической системы определяет характер этой динамики системы. Аттрактор в виде точки соответствует стабильному стационарному состоянию. системы (настройки системы не изменяются). Аттрактор в виде замкнутой кривой описывает регулярные циклические колебания системы. Странный аттрактор описывает сложные непериодические колебания системы Важной задачей является реконструкция аттрактора системы по данным временного ряда. Согласно теории Такенса-Мане удовлетворительную геометрическую картину аттрактора системы можно получить, если вместо переменных, характеризующих поведение системы (но значения которых нам неизвестны), использовать так называемые векторы
задержек 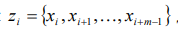для одного измеряемого параметра.

Впервые даный подход к анализу временных рядов был математически обоснован в работах Такенса. Теория Такенса позволяет установить динамический характер системы.
Для исследования динамических характеристик системы необходимо выполнить
погружение системы в фазовое пространство Для этого используют метод временных задержек (лагов).

Фазовое пространство размерности D строят, используя один временной ряд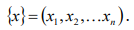

. При значении лага L = 1 первый вектор столбец имеет вид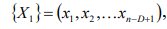

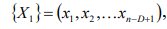
, второй столбец имеет вид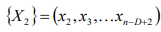
, последний столбец имеет вид

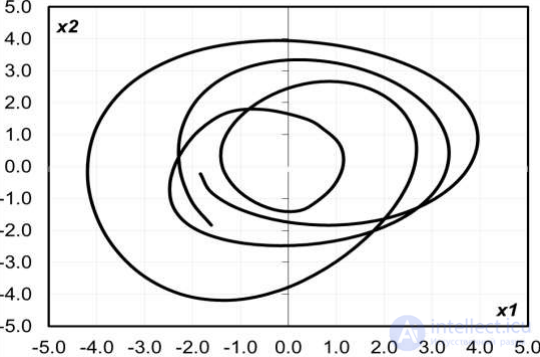
Рис. 7.5. Двухмерная проекция фазового портрета системы зернопроизводства Украины

Два отрезка временного ряда, смещенные друг относительно друга на некоторый лаг 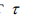можно рассматривать как разные параметры x1 и x2.

Рассмотрим плоскость 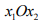, координатами которой выступают элементы рядов X1 и X2

. График зависимости 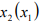образует фазовую траекторию системы. D отрезков временного ряда, смещенных на лаг 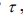, образуют D-мерную модель (реконструкцией) фазового портрета системы.

Перед построением фазового портрета из реальных временных рядов их необходимо сглаживать. На рис. 7.5 изображена двумерная проекция фазового портрета системы зернопроизводства Украины, полученного из совокупности сглаженных рядов остатков. Поведение фазовой траектории системы показывает ярко выраженную цикличность.

Определение размерности системы.

Для анализа системы необходимо прежде всего установить ее размерность, то есть минимальное количество параметров, необходимое для описания системы. Малое значение размерности указывает на детерминированность системы, большое – на ее случайность. При размерности, не превышающей 5 – 6, хорошо работают разнообразные методы анализа и прогноза эволюции системы Обычно явный вид математической модели системы неизвестен и, поэтому, необходимо иметь возможность оценивать размерность системы непосредственно по наблюдениям. Для определения размерности используют метод "фальшивых соседей" и метод собственных значений. В методе фальшивых соседей используют понятие близости фазовых векторов. Для определения расстояния между векторам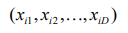и
и используют евклидовое определение расстояния

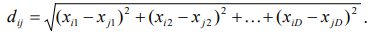. (7.7)

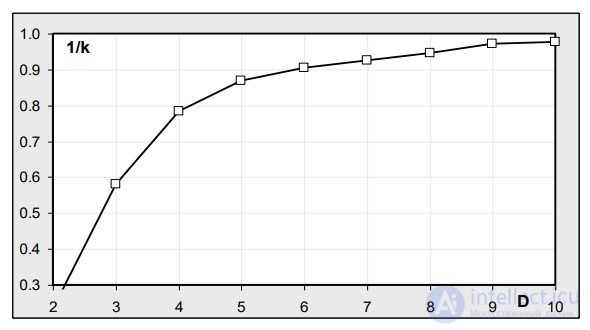
Рис. 7.6. Определение минимальной размерности вложения D

При увеличении размерности фазового пространства D в результате появления новых ненулевых координат происходит увеличение расстояния между двумя точками. пространства – эффект растяжения фазового пространства. Процедура оценки размерность системы начинается с размерности 2. Выбирается группа векторов фазового пространства, расстояние между которыми наименьшее – ”ближайшие соседи”. Затем размерность увеличивается на 1 и рассчитывается коэффициент k увеличения расстояния между векторами – ”ближайшими соседями”. За размерность системы выбирают такое число D
, чтобы при переходе к размерности D +1 расстояние между ”ближайшими соседями” увеличивалось незначительно (менее 10%). К примеру, на рис. 7.6 видно, что при D > 4
рост расстояния между ”векторами-соседями” незначительно. Поэтому размерность вложения системы зернопроизводства
Украину можно оценить значением 4.

Метод собственных значений.

Для реализации метода сначала приведем ряд к нулевой средней, то есть произведем замену
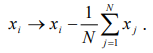. (7.8)
После этого сформируем из полученного ряда матрицу наблюдений M по следующему правилу:
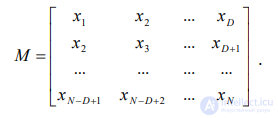. (7.9)
В строках этой матрицы стоят компоненты реконструированных по временному ряду векторов.

Размерность реконструкции ( D = 8 ) выберем заведомо больше ожидаемой размерности системы На основе матрицы M
сформируем матрицу ковариации
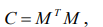, (7.10)
и вычислим ее собственные значения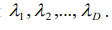
. Расчеты собственных значений можно выполнить в Matlab с использованием функции eig(С), возвращающей вектор собственных значений квадратной матрицы С.

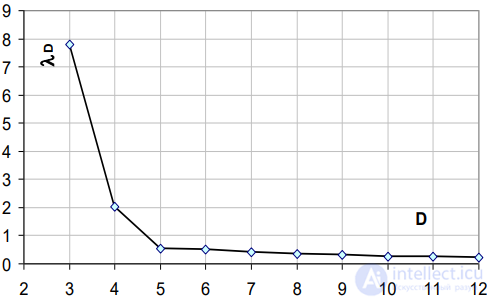
Рис. 7.7. Определение размерности вложения методом собственных значений

Как правило, несколько первых собственных значений будут заметно больше. от других, которые примерно одинаковы. При некотором номере собственного значения величины собственных значений стабилизируются (выходят на плато). Этот номер и будет являться размерностью системы. Результаты расчетов методом собственных значений приведены на рис. 7.7. Как видно из рисунка,

при D >5 величины собственных значений стабилизируются.

Следовательно значение D = 5 и является значением размерности исследуемой системы.
Определение максимального показателя Ляпунова. Фундаментальной характеристикой динамической системы есть набор показателей Ляпунова, которые описывают
поведение траекторий в фазовом пространстве. Показатели Ляпунова отмечаются символами 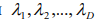и могут быть отрицательными, положительными и нулевыми. Количество характеристик Ляпунова равно размерности системы. Каждый показатель отображает среднюю скорость разбегания ( 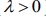) или восхождение ( ) начально близких фазовых траекторий в некоторой плоскости.

Значение максимального показателя Ляпунова позволяет идентифицировать тип динамики системы:
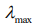< 0 система эволюционирует в состояние равновесия,

при 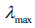= 0 динамика системы является циклической,

в случае, когда 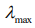> 0 , динамика системы хаотична.

Знание максимального показателя Ляпунова системы очень важно, поскольку он определяет возможность прогнозирования развития системы.

Во первых в двух случаях система прогнозируема, причем мы можем прогнозировать ее развитие на произвольно большой промежуток времени. При наличии хаотической динамики
в системе максимальное время прогнозирования ограничено вследствие быстрого разбегания фазовых траекторий. Значение максимального прогнозного горизонта
Tmax определяется из соотношения Tmax =1/λmax

. Например, для системы зернопроизводства Украины λmax= 0.05 и максимальный горизонт прогнозирования составляет Tmax= 20 лет.

Исследование, описанное в статье про идентификация систем, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое идентификация систем, сложные системы и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Системный анализ (системная философия, теория систем)

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.