Алгоритмы определения комплексов с использованием матриц путей на графе кратко

Привет, Вы узнаете о том , что такое алгоритмы определения комплексов с использованием матриц путей на графе, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое алгоритмы определения комплексов с использованием матриц путей на графе , настоятельно рекомендую прочитать все из категории Системный анализ (системная философия, теория систем).

Последовательность сцепленных дуг, позволяющая пройти из одной вершины в другую, называется путем. Так, на рассматриваемом графе путем из вершины 1 в вершину 4 будет последовательность дуг 1-2, 2-3, 3-4. Путь также можно изобразить последовательностью вершин, которая их содержит, например, путь 1,2,3,4,3 или путь 1, 2, 3, 4, 5. Длиной пути называется число дуг на пути. Например, путь из вершины 1 в вершину 7 имеет длину, равную 6.

Рис. 1. Ориентированный граф

Путь, начальная вершина которого совпадает с конечной, причем каждая вершина, за исключением начальной, проходится один раз, называется контуром. В рассматриваемом графе можно выделить следующие контуры:

(2, 3,4, 2), (3,4,3), (6, 7.6). ????

Контуры графа, имеющие хотя бы одну общую вершину, называются связан-ными. Система связанных контуров графа образует комплекс. Для любых двух вершин, входящих в комплекс, существует соединяющий их путь. Так, контуры ( 2, 3, 4, 2 ) и ( 3. 4, 3 ) являются' связанными, так как они имеют, по крайней мере, одну общую вершину, например, вершину 3 (или вершину 4), поэтому вершины 2, 3, 4 образуют комплекс Легко убедиться, что для любых двух вершин этого комплекса существует соединяющий их путь. Например, возьмем две вершины 2 и 4. Из вершины 2 в вершину 4 ведет путь 2.-3,3-4,а из вершины 4 в вершину 2 -путь 4-2. Комплекс соответствует элементам, которые могут быть рассчитаны только совместно

Алгоритмы выделения комплексов используют основное свойство вершин графа, принадлежащих комплексу для любых двух вершин I и J, входящих в комплекс, должен существовать путь из I-й в J-ю вершину и обратный путь из J-и в I-ю вершину (естественно двигаясь в направлении ориентированных дуг). Для выделения комплексов существуют различные матричные алгоритмы [1-3].Некоторые из них связаны с представлением структуры ХТС в виде матрицы связи и последующими операциями с этой матрицей с целью выделения на графе ХТС путей различной длины и построения матрицы комплексов.

В основе других алгоритмов лежит использование матрицы путей на графе. Матрица путей является квадратной и содержит столько столбцов, сколько элементов имеется в составе ХТС. Если на графе есть путь любой длины из вершины I в вершину J, то на пересечении I-й строки и J-го столбца матрицы путей ставится 1, иначе - 0. На главной диагонали этой матрицы ставятся единицы, так как считается, что путь длиной 0 из любого элемента в этот же самый элемент всегда существует. Матраца путей графа ХТС, представленной на рис. 2 (обозначим эту матрицу буквой Р), имеет вид:

P=	1	1	1	1	1	1	1
	0	1	1	1	1	1	1
	0	1	1	1	1	1	1
	0	1	1	1	1	1	1
	0	0	0	0	1	1	1
	0	0	0	0	0	1	1
	0	0	0	0	0	1	1

Наряду с матрицей Р строится вспомогательная матрица S. Об этом говорит сайт https://intellect.icu . Она является транспонированной по отношению к матрице Р, т- е. столбцы матрицы S являются строками матрицы Р:

Элементы матрицы Р указывают на наличие пути из I вершины в J-ю вершину, а элементы матрицы S - из J-й вершины в I-ю. Логически перемножая элементы матриц Р и S ( полагая 0 * 0 = 0, 0 * 1 = 0, 1 * 0 = 0, 1 * 1 = 1 ), получим матрицу D выделения комплексов:

С помощью матрицы D определяются комплексы, входящие в состав графа ХТС, по следующим правилам:

- если в I-ой строке этой матрицы имеется только один не нулевой элемент d(1,1)=1 ( принадлежащий главной диагонали ), то элемент ХТС с номером I может быть рассчитан отдельно от остальных элементов системы. В рассматриваемом примере это элементы 1 и 5.

- строки матрицы D, имеющие, кроме элемента d (1,1), другие не нулевые элементы, соответствуют комплексам. Не нулевые элементы строк указывают вершины графа, входящие в состав комплекса.

В нашем примере, согласно матрице D, в состав ХТС входят два комплекса:

комплекс 1 - ( 2, 3, 4 ) и комплекс 2 - ( 6, 7 ).

Одинаковые строки матрицы соответствуют одному и тому же комплексу.

Пример 2

Рассмотрим три любые вершины графа ХТС: I, J, M. Если существует путь любой длины из вершины I в вершину J и из вершины J в I, то эти вершины принадлежат одному и тому же комплексу К. Для присоединения вершины M к комплексу необходимо проанализировать, есть ли путь из любой вершины ( например, I принадлежащей комплексу К, в вершину M и обратный путь из вершины M в любую вершину комплекса К (например, I). Если эти два пути существуют, то вершина M принадлежит комплексу К

Применение этого правила к ХТС, изображенной на рис. 3, позволяет выделить следующие комплексы: - комплекс К1- ( 1,2, 3, 8, 9, 10 ), комплекс К2 - (5,11 ) , элементы 4,6, 7 рассчитываются автономно.

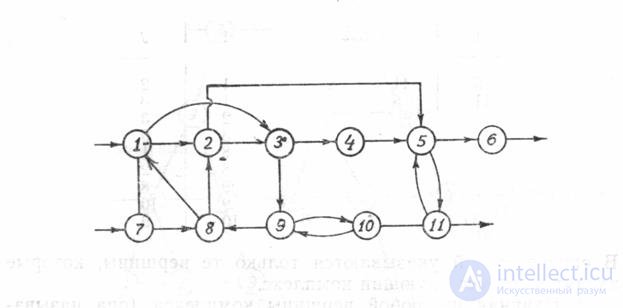
Рис. 2. Граф некоторой замкнутой ХТС

Определение предварительной последовательности расчета ХТС.

После выделения комплексов определяют предварительную последовательность расчета ХТС. Совокупность вершин, входящих в комплекс, объединяют в одну новую вершину, в результате чего получается граф, не содержащий контуров ( рис. 3 ).

Рис.3. Определение ППРС.

Такой граф соответствует разомкнутой ХТС. Поэтому определение предварительной последовательности расчета замкнутой системы ( ППРС) производится по алгоритмам, применяемым в структурном анализе разомкнутых ХТС.

Для рассмотренной системы имеем : ППРС - [ 7, ( 1, 2. 3, 8, 9, 10 ), 4, ( 5, 11 ), 6 ]

пример 3

Структуру ХТС обычно рассматривают в терминах теории графов, т.е. в виде ориентированного графа, вершины которого соответствуют аппаратам, а дуги – потокам (например, так как на Рис.4.2). На Рис.4.2 номера вершин обозначены большим курсивом (справа сверху от вершины), а номера потоков – малым прямым шрифтом (под линией соответствующего потока).

Рис.4.2. Представление ХТС в виде ориентированного графа

Последовательность сцепленных дуг, позволяющая пройти от одной вершины к другой, называется путем. Путь можно обозначить как через последовательность дуг, так и через последовательность вершин. Путь, начальная вершина которого совпадает с конечной, причем каждая вершина, за исключением начальной, проходится только один раз, называется контуром. Например, на Рис.4.2 имеются три контура (по вершинам): 2-3-4-2, 3-4-3 и 6-7-6.

Комплексом, называется часть графа, вершины которого обладают следующими свойствами:

- каждая из вершин и дуг комплекса входит в один из контуров графа;

- если вершина i входит в комплекс, то в этот комплекс входят также все вершины, входящие в контуры, которые содержат вершину i.

Например, на графе, представленном на Рис.4.2 имеются два комплекса (по вершинам): 2-3-4 и 6-7. В первый комплекс входят два контура (2-3-4-2 и 3-4-3), а во второй – один (6-7-6).

пример 4

Выводы из данной статьи про алгоритмы определения комплексов с использованием матриц путей на графе указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое алгоритмы определения комплексов с использованием матриц путей на графе и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Системный анализ (системная философия, теория систем)

Из статьи мы узнали кратко, но содержательно про алгоритмы определения комплексов с использованием матриц путей на графе