Оптимизация систем с учетом риска

оптимизация систем с учетом риска — это подход, направленный на улучшение работы сложных систем, при этом учитывая возможные риски и неопределенности. Основная цель — найти баланс между эффективностью системы и управлением рисками для минимизации потерь или возможных негативных последствий. Этот процесс может включать несколько шагов:

1. Идентификация рисков: Определение возможных факторов риска (внешних и внутренних), которые могут повлиять на систему. Это может включать финансовые, технические, экологические и другие виды рисков.

2. Оценка вероятностей и последствий: Для каждого риска определяются его вероятность и возможные последствия для системы. Здесь применяются вероятностные методы и анализ данных.

3. Определение критериев оптимизации: Необходимо установить целевые функции для оптимизации, которые включают как минимизацию рисков, так и максимизацию производительности системы.

4. Разработка моделей и методов: Применяются различные математические и статистические методы, такие как методы линейного и нелинейного программирования, стохастические модели, методы Монте-Карло и другие.

5. Мониторинг и контроль: После внедрения оптимизированного решения проводится постоянный мониторинг для оценки того, как система справляется с рисками на практике.

Методы оптимизации систем с учетом риска:

• Робастная оптимизация: Предполагает создание решений, которые остаются эффективными при изменении условий или при наличии неопределенностей.
• Стохастическая оптимизация: Учитывает вероятностные распределения и неопределенности в параметрах модели.
• Оптимизация на основе сценариев: Включает разработку нескольких сценариев для моделирования различных возможных исходов и принятие решений с учетом наихудших сценариев.

Этот подход может применяться в разных областях, таких как:

• Финансовые системы (управление портфелем активов с учетом риска),
• Энергетика (управление энергосетями с учетом отказов),
• Промышленность (управление рисками в производственных процессах).

Оптимизация финансовых систем с учетом риска (управление портфелем активов с учетом риска)

В управлении портфелем активов с учетом риска основная задача состоит в нахождении оптимального соотношения между доходностью и риском. Это позволяет инвесторам минимизировать возможные потери, сохраняя при этом приемлемый уровень доходности. Процесс включает в себя следующие ключевые этапы:

1. Оценка риска

Для управления рисками в финансовом портфеле используются различные метрики:

• Волатильность: Измеряет колебания доходности активов. Чем выше волатильность, тем выше риск.
• Value-at-Risk (VaR): Оценивает максимальные возможные убытки портфеля при определенном уровне доверия (например, 95% или 99%) за определенный период.
• Conditional Value-at-Risk (CVaR): Оценивает средние потери, превышающие VaR. Эта метрика позволяет оценить серьезные убытки, когда они действительно происходят.
• Beta: Показывает, насколько активы в портфеле коррелируют с общим рынком. Активы с высоким бета-коэффициентом подвержены большему рыночному риску.

2. Определение целевой доходности

Важно установить желаемую доходность на основе инвестиционных целей. В процессе управления портфелем стоит учитывать, что более высокие доходности часто сопряжены с повышенными рисками.

3. Оптимизация портфеля

На основе заданных уровней риска и доходности применяются различные методы оптимизации:

• Модель Марковица (Среднее-Вариация): Эта классическая модель оптимизации портфеля предполагает нахождение портфеля с минимальной волатильностью для заданного уровня доходности. Она основывается на расчете ковариаций между активами для создания эффективной границы (efficient frontier), которая определяет портфели с наилучшим соотношением доходности и риска.

• Модель Шарпа: Эта модель использует коэффициент Шарпа, который измеряет доходность портфеля с поправкой на риск, чтобы выбрать оптимальный портфель. Чем выше коэффициент Шарпа, тем лучше портфель компенсирует риск.

• Оптимизация с учетом VaR и CVaR: Более сложные модели оптимизации могут учитывать не только волатильность, но и возможные крайние убытки. Это особенно полезно в условиях нестабильных рынков.

• Робастные методы: Для учета неопределенностей в параметрах (например, волатильности или корреляций активов) можно использовать робастную оптимизацию, которая создает портфели, устойчивые к изменению рыночных условий.

4. Диверсификация

Диверсификация является ключевым инструментом управления рисками. Важно распределить активы по различным классам (акции, облигации, товары и т. д.) и регионам, чтобы снизить общий риск портфеля. Это уменьшает вероятность того, что негативное событие в одной области сильно повлияет на весь портфель.

5. Мониторинг и пересмотр портфеля

После формирования оптимизированного портфеля необходимо регулярно мониторить его производительность и корректировать структуру в зависимости от изменения рыночных условий, а также от изменений в предпочтениях инвестора по уровню риска.

Применение технологий и алгоритмов:

• Алгоритмическая торговля: Использование алгоритмов для автоматического ребалансирования портфеля на основе предопределенных критериев риска и доходности.
• Искусственный интеллект и машинное обучение: Эти технологии позволяют более точно прогнозировать рыночные риски и находить скрытые корреляции между активами.

Пример:

Если инвестор готов принять умеренный уровень риска, можно создать портфель с диверсифицированной структурой, включающий акции с низким Beta и высококачественные облигации. Использование CVaR поможет избежать значительных убытков в периоды рыночной нестабильности.

Оптимизация портфеля активов с учетом риска помогает инвесторам принимать более взвешенные решения, учитывая их склонность к риску и рыночные условия.

Оптимизация энергетических систем с учетом риска (управление энергосетями с учетом отказов),

В энергетике управление энергосетями с учетом рисков и возможных отказов — ключевая задача для обеспечения надежного и эффективного снабжения потребителей. Современные энергосистемы становятся все более сложными из-за интеграции возобновляемых источников энергии, что увеличивает неопределенность и вероятность отказов. Оптимизация таких систем с учетом рисков помогает снизить вероятность нарушений и минимизировать последствия в случае отказов.

Основные риски в энергосетях:

1. Технические отказы: Включают поломки оборудования (линий электропередачи, трансформаторов, генераторов) и отказ работы подстанций.
2. Непредсказуемость источников энергии: Ветро- и солнечная энергетика подвержены изменению погодных условий, что затрудняет планирование энергоснабжения.
3. Киберугрозы: Энергосистемы становятся более зависимыми от цифровых технологий, что увеличивает уязвимость для кибератак.
4. Природные катаклизмы: Ураганы, наводнения и другие природные явления могут разрушить инфраструктуру энергосетей.
5. Человеческий фактор: Ошибки операторов или неправильное планирование также могут привести к серьезным отказам.

Методы оптимизации управления энергосетями с учетом рисков:

1. Риск-ориентированное планирование (Risk-Based Planning)

Этот метод предполагает интеграцию оценки рисков на этапе проектирования и планирования энергосетей. Включает прогнозирование возможных сбоев и определение мер для их предотвращения.

• Оценка надежности (Reliability Assessment): Анализирует, насколько устойчива система к отказам и каким образом можно улучшить ее надежность. Это включает вычисление таких показателей, как SAIDI (средняя продолжительность отключений) и SAIFI (средняя частота отключений).

2. Стохастические модели оптимизации

Эти модели учитывают неопределенности, такие как погодные условия и непредсказуемость потребления. Стохастическая оптимизация помогает найти решения, которые устойчивы к различным сценариям развития событий.

• Monte Carlo Simulation: Используется для моделирования множества возможных сценариев отказов и оценки вероятности их возникновения. Это помогает понять, как разные факторы (например, внезапные нагрузки или погодные условия) могут повлиять на энергосистему.

3. Оптимизация распределения нагрузки (Load Shedding Optimization)

Когда система близка к перегрузке или происходит отказ в одном из ее узлов, важно правильно распределить нагрузки для минимизации ущерба. В таких случаях применяется оптимизация распределения энергии:

• Реализация механизмов "умного отключения": Системы могут быть настроены на отключение незначительных потребителей в моменты пиковых нагрузок или при авариях.

4. Использование робастной оптимизации

Робастные модели оптимизации разрабатываются для того, чтобы учесть неопределенности и поддерживать стабильность системы даже в условиях изменения параметров. Например, они могут учитывать резкие изменения в производстве энергии от возобновляемых источников.

5. Интеграция распределенных энергетических ресурсов (DER)

Включение распределенных энергетических ресурсов (таких как солнечные панели, ветровые установки, аккумуляторы) может повысить надежность энергосетей. Децентрализованное производство энергии снижает зависимость от крупных генераторов и может использоваться как резерв в случае отказов.

• Микросети (Microgrids): Локализованные микросети могут работать независимо или подключаться к основной энергосети, помогая балансировать спрос и предложение при сбоях в главной сети.

6. Предиктивное техническое обслуживание (Predictive Maintenance)

Сбор данных с различных частей сети (с помощью датчиков и IoT-устройств) позволяет предсказывать и предупреждать возможные отказы оборудования. Это помогает не только сократить расходы на ремонт, но и повысить общую надежность системы.

• Прогнозирование отказов (Failure Forecasting): Анализ исторических данных о работе системы и текущих показателей помогает предсказать, где и когда может произойти сбой.

7. Кибербезопасность

С учетом увеличивающегося числа кибератак на энергосистемы, важную роль играет защита данных и сетей. Надежные механизмы обнаружения и предотвращения киберугроз могут предотвратить отключения и нарушения.

8. Оптимизация восстановительных мероприятий (Restoration Planning)

В случае возникновения сбоев, системы восстановления играют ключевую роль в минимизации простоев. Оптимизация планов восстановления включает в себя определение приоритетов для восстановления критических элементов сети.

Пример применения:

Предположим, в энергосети используются источники энергии из возобновляемых и традиционных генераторов. Для учета риска отказов, связанных с ветровыми электростанциями, можно разработать модель, которая включает стохастическое прогнозирование скорости ветра и распределения нагрузки. В случае, если ветер недостаточен, система может автоматически переключаться на другие источники, используя методы оптимизации для минимизации издержек и обеспечения стабильности.

Технологии:

• Машинное обучение: Используется для анализа больших данных, поступающих с датчиков, и предсказания потенциальных сбоев.
• Искусственный интеллект: Помогает в принятии решений при распределении энергопотоков и оптимизации работы сети.
• IoT: Сети сенсоров и умных устройств могут собирать данные в реальном времени и быстро реагировать на изменения в сети.

Заключение:

Оптимизация управления энергосетями с учетом рисков направлена на повышение их устойчивости и надежности. Методы, включающие анализ данных, моделирование отказов и прогнозирование нагрузок, помогают минимизировать влияние сбоев на потребителей и обеспечить стабильность работы энергосистем.

Оптимизация промышленных систем с учетом риска (управление рисками в производственных процессах).

Управление рисками в производственных процессах является критически важной задачей для обеспечения бесперебойной работы, безопасности и качества продукции. Современные предприятия сталкиваются с множеством рисков, которые могут повлиять на эффективность производства, затраты и репутацию компании. Эти риски могут включать технические сбои, несоблюдение стандартов безопасности, изменения на рынке или перебои в цепочке поставок.

Основные типы рисков в производстве:

1. Технологические риски: Включают поломки оборудования, дефекты продукции, нестабильность процессов и отказ технологий.
2. Операционные риски: Ошибки при управлении производственными операциями, неверное планирование, нехватка квалифицированного персонала.
3. Финансовые риски: Увеличение производственных затрат, рост цен на сырье, колебания обменных курсов.
4. Риски безопасности: Опасности для здоровья и жизни работников, несоблюдение стандартов безопасности.
5. Риски в цепочке поставок: Перебои с поставками сырья, сбои у поставщиков и транспортные задержки.
6. Экологические и регуляторные риски: Несоблюдение экологических стандартов и регуляторных требований, штрафы и санкции.
7. Киберриски: Угрозы информационной безопасности и кибератаки на системы автоматизации.

Методы управления рисками в производстве:

1. Идентификация и оценка рисков

Управление рисками начинается с их идентификации и оценки. Необходимо выявить потенциальные риски на всех этапах производственного процесса, от закупки сырья до выпуска готовой продукции.

• SWOT-анализ: Определяет сильные и слабые стороны производства, а также внешние возможности и угрозы.
• FMEA (Failure Mode and Effects Analysis): Метод анализа возможных отказов и их последствий для производственного процесса, который помогает выявить наиболее критичные точки.

2. Стохастическое моделирование и анализ данных

Для оценки вероятности рисков и их последствий используется стохастическое моделирование. Это помогает прогнозировать потенциальные сбои и разработать стратегию реагирования.

• Методы Монте-Карло: Применяются для моделирования различных сценариев рисков и расчета их вероятностей, что помогает принимать взвешенные решения в условиях неопределенности.

3. Оптимизация производственных процессов

Один из методов управления рисками — это оптимизация производственных процессов, направленная на повышение их устойчивости к сбоям.

• LEAN-методология: Использует принципы бережливого производства для минимизации отходов и повышения эффективности. Это уменьшает риски, связанные с избыточными затратами и потерями времени.
• Шесть Сигм (Six Sigma): Стратегия управления качеством, которая фокусируется на минимизации дефектов в процессе производства. Применение этого метода помогает снижать риски, связанные с качеством продукции.

4. Автоматизация и цифровизация производства

Автоматизация процессов и внедрение цифровых технологий снижают риски человеческих ошибок и повышают точность операций.

• SCADA-системы: Позволяют автоматизировать мониторинг и управление оборудованием в реальном времени, что помогает оперативно реагировать на отклонения и предупреждать сбои.
• Цифровые двойники: Модели реальных производственных процессов в цифровой среде, которые позволяют тестировать изменения и прогнозировать их последствия без риска для реального производства.

5. Предиктивное техническое обслуживание (Predictive Maintenance)

Использование предиктивных технологий для предотвращения поломок оборудования до того, как они приведут к серьезным сбоям, становится важным инструментом управления рисками.

• Анализ данных с сенсоров: Данные, полученные с датчиков, помогают предсказывать, когда оборудование может выйти из строя, позволяя провести ремонт заранее и избежать простоя.
• Машинное обучение: Технологии ИИ могут анализировать данные и выявлять скрытые закономерности, предсказывая возможные отказы и поломки.

6. Управление цепочкой поставок (Supply Chain Risk Management)

Для минимизации рисков, связанных с поставками, важно иметь стратегии управления цепочкой поставок.

• Диверсификация поставщиков: Включение нескольких источников сырья или компонентов позволяет снизить зависимость от одного поставщика и уменьшить риск перебоев.
• Применение технологий отслеживания: RFID-метки и IoT-устройства позволяют отслеживать перемещение материалов и готовой продукции в режиме реального времени, что снижает риск потерянных или задержанных поставок.

7. Кибербезопасность

С учетом увеличивающейся зависимости от информационных технологий, особенно при использовании IoT и цифровых систем управления, критически важно защищать производственные системы от кибератак.

• Защищенные сети и шифрование данных: Обеспечивают защиту информации и предотвращают несанкционированный доступ к производственным системам.
• Оценка и управление киберрисками: Регулярное тестирование систем безопасности и обучение сотрудников по предотвращению инцидентов информационной безопасности.

8. Мониторинг и контроль

Для эффективного управления рисками необходим постоянный мониторинг производственных процессов и анализ данных в реальном времени.

• KPIs (ключевые показатели эффективности): Использование показателей для отслеживания производственных процессов и оценки их эффективности. Например, время простоя оборудования, процент брака, выполнение сроков и т. д.
• Системы раннего предупреждения: Включают датчики и системы, которые сообщают об отклонениях в параметрах оборудования или процессов до того, как произойдет сбой.

Пример:

Производственная компания, которая зависит от сложной цепочки поставок, может использовать цифровые двойники для моделирования своих процессов. С помощью предиктивного технического обслуживания она может предотвратить поломки оборудования, а с помощью анализа данных — выявить наиболее уязвимые точки в цепочке поставок. Автоматизация управления с использованием SCADA-систем позволяет отслеживать статус оборудования в реальном времени, уменьшая риск незапланированных простоев.

Технологии и решения:

• Искусственный интеллект (AI): Для анализа данных и прогнозирования рисков.
• Машинное обучение (ML): Для выявления закономерностей и предсказания отказов оборудования.
• Big Data: Для обработки больших объемов данных в реальном времени, связанных с производственными процессами.
• IoT (Интернет вещей): Для интеграции датчиков и устройств, отслеживающих состояние оборудования и материалов.

Заключение:

Управление рисками в производственных процессах позволяет улучшить надежность и эффективность работы предприятия, минимизировать издержки и повысить безопасность. Оптимизация процессов, внедрение предиктивных технологий и автоматизация могут значительно снизить влияние потенциальных рисков на производство.

8.1. Задача линейного программирования

Оптимизация систем – это комплекс методов, позволяющих выбрать из многих возможных вариантов использования ресурсов один – самый лучший с точки зрения
получение экономического результата с наименьшими издержками.
Продемонстрируем методику оптимизации на примере экономических систем.
Каждая экономическая система преследует цель своего функционирования. Чаще всего – это
получение максимальной прибыли или минимальные затраты. Существует некоторая функция F, которая описывает степень достижения цели и выражена через входные переменные и
параметрами системы:
(8.1)

Здесь xj (j=1,2,...,n) - управляемые переменные, поддающиеся управлению; yi (i=1,2, ..., m) -
неуправляемые переменные, значения которых определяются внешней средой;

c1 ,c2 , ,ci ...- параметры системы, которые неизменны.

Например, посевная площадь – управляемая переменная, а температура воздуха – неуправляемая переменная; качественный состав почвы – параметр системы.
В общем виде задача экономико-математического моделирования формулируется следующим образом:
Найти следующие значения управляемых переменных xj , при которых целевая функция F
приобретает максимальное или минимальное значение :
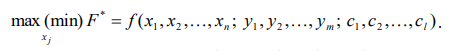. (8.2)
Целевая функция F определяет эффективность функционирования системы.
Возможности выбора xj всегда ограничены внешними условиями. К примеру, площадь посева ограничена наличием пашни и других ресурсов. Эти процессы
можно описать системой математических неравенств (или уравнений) вида:
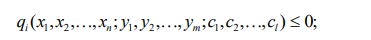(8.3а)
или
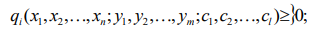(8.3б)

Система (8.3а) – (8.3б) называется системой ограничений задачи. Для экономических систем переменные xj
должны быть неотъемлемыми:
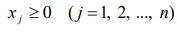. (8.4)
Зависимости (8.2) – (8.4) образуют экономико-математическую модель задачи линейного программирования для экономической системы.
Любой набор переменных x1, x2, ..., xn, удовлетворяющий условиям (8.3) и (8.4),
называют допустимым планом. Каждый допустимый план определяет некоторую стратегию поведения экономической системы. Каждому допустимому плану отвечает
значение целевой функции, вычисляемое по формуле (8.2).
Совокупность всех решений системы ограничений (8.3) и (8.4) образует область допустимых планов.
План, для которого целевая функция приобретает экстремальное значение, называется оптимальным. Оптимальный план является решением задачи линейного программирования (8.2) – (8.4).
Решение задачи линейного программирования ищут с помощью симплекс-метода. Этот способ реализован в пакете Excel – Данные, Поиск решения.

8.2. Неопределенность и риск в экономике

Экономические системы находятся в условиях неопределенности. Это значит, что нам не известно, в каком состоянии будет система в будущий момент времени. Так неопределенность всегда рождает риск. Это может быть риск недополучения прибыли, риск потерь, риск неиспользованных возможностей и т.д.
Принятие решений в условиях неопределенности характеризуется тем, что невозможно однозначно предусмотреть их последствия. В результате прибыль становится случайной или нечеткой величиной, которую можно максимизировать только при условии учет вероятности различных вариантов развития событий, степени определенности разных признаков, учет склонности к риску лица, принимающего решение.
Причины возникновения неопределенности и обусловленного ею риска делятся на три группы.

Первая группа. Большинство связанных с экономикой процессов случайны. Трудно предусмотреть различные природные явления, изменения климата, политические события,
изменения конъюнктуры мирового рынка, появление новых технологий, изменения вкусов потребителей и т.д.

Вторая группа. Можно говорить об экономически оптимальной неполноте
информации, потому что нередко более целесообразно работать с неполной информацией, чем
собирать очень дорогую практически полную информацию. Неполнота информации может
быть обусловлена ​​также неполным ее пониманием или неумением обработать ее на
компьютере. Кроме того, всякая информация всегда неточна (статистика, выборочные наблюдения, экспертные оценки).

Третья группа. Существует так называемая асимметрия информации. Крупные игроки экономического рынка считают целесообразным скрывать от потребителей некоторую часть информации по экономическим, политическим или другим причинам.

Роль информации в процессе принятия решений чрезвычайно велика.
Особую цену имеет релевантная (правдивая, важная) информация, которая доступна узком кругу лиц. После опубликования такой информации широкие массы предпринимателей используют ее для принятия бизнес-решений и данная информация быстро теряет свою ценность. Нехватка информации (неопределенность) всегда порождает риск. С риском приходится сталкиваться в повседневной практической деятельности.
Его невозможно избежать ни в одном из видов деловой активности. Риск присутствует при принятии решений по размещению денег в банке, при покупке акций и других ценных бумаг, при инвестировании средств в новое производство и т.д.

Бездействие в сфере бизнеса связано с риском неиспользованных возможностей. Заметим, что риск существует только тогда, когда есть разные варианты развития событий.
Есть разные подходы к определению риска. По определению В. Маршалла риск – это вероятность реализации неблагоприятного события. Э. Дж. Хенли, Х. Кумамото рассматривают риск как вероятность материального ущерба или повреждений. Часто риск понимают не только как возможность наступления ущерба, но и как
возможность отличия от цели, отсутствие ожидаемых результатов.
Обобщая, можно сказать, что риск – это осознанная опасность
наступление событий с нежелательными последствиями. Риск – величина количественная и определяется умножением вероятности негативного события на величину возможного ущерба от него.
В 60-х годах ХХ века развились такие направления науки, как теория случайных процессов, теория нечетких множеств, теория игр, теория статистических
решений. Эти научные дисциплины позволили оптимизировать управление экономическими системами с учетом присущих им неопределенности и риска.

8.3. Модель Марковица.

Большинство инвесторов инвестируют обычно несколько объектов реального или финансового сектора, формируя совокупность активов (инвестиционный портфель)
Портфельный подход предполагает максимизацию полезности от активов, т.е. рост их доходности при диверсификации (разнообразии) с целью
понижение инвестиционных рисков. Снижение рисков путем комбинации активов реализует принцип, отвечающий пословице «не неси все яйца в одной корзине» (вероятность уронить две корзины значительно меньше, чем вероятность упустить один). Таким образом, достигают компромисса таких на первый взгляд несовместимых целей, как максимизация дохода и минимизация риска.
Лауреат Нобелевской премии Гарри Марковиц впервые указал на то, что при формировании портфеля ценных бумаг необходимо учитывать не только их доходность но и степень риска. Основными параметрами модели Марковица является доходность
и рискованность ценных бумаг, входящих в портфель. Модель Марковица основывается на следующих предположениях:

• доходности ценных бумаг распределены по нормальному закону;
• прошлые значения, использованные в расчетах доходности и риска, полностью отражают будущие значения доходности и риска.

Доходность портфеля ценных бумаг – это средневзвешенная доходность.
бумаг, входящих в портфель, определяется по формуле:
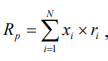, (8.5)
где:
N ‒ количество ценных бумаг, входящих в портфель;

xi ‒ процентная доля данной бумаги в портфеле ();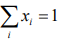

ri ‒ доходность данной бумаги.

Доходность данного вида акций ri на минимальном временном промежутке (1 день или 1 неделя) обычно рассчитывается по соотношению
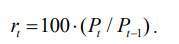. (8.6)
Здесь Pt-1 - цена акции в предыдущий момент времени,
Pt – цена акции в следующий момент времени.

При длительных наблюдениях доходность ценной бумаги оценивают как среднее значение за период наблюдений
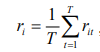, (8.7)

где
T – количество временных промежутков.
Риск финансовых операций напрямую зависит от изменчивости внешних условий
и стоимости ценных бумаг. Чем больше эта изменчивость, тем больше риск финансовых операций.

В модели Марковица риск ценной бумаги рассматривается как среднеквадратическое отклонение доходности от ее математического ожидания.
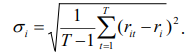. (8.8)
Для оценки риска портфеля необходимо учесть как риски отдельных акций, так и корреляционные риски. Последние связаны с тем, что потери могут возрасти, если цены
акций будут вести себя коррелированно и могут одновременно упасть. Коэффициент корреляции между двумя ценными бумагами рассчитывается по формуле
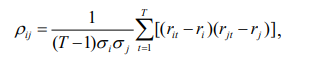, (8.9)
где:
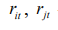— доходность ценных бумаг i да j в период t

. Тогда общий риск портфеля ценных бумаг определяется функцией среднеквадратичного отклонения:
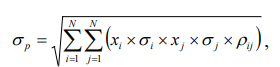, (8.10)
где:
ixi , xj ‒ процентная доля данных бумаг в портфеле;
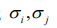, ‒ риски данных бумаг (среднеквадратические отклонения);
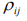‒ коэффициент линейной корреляции между доходностями r it да r jt .

Невозможно одновременно добиться максимального и минимального дохода риска. Потому задачу решают поэтапно: ограничивают один параметр и оптимизируют другой. Таким образом рассматривают два подхода к решению задачи об оптимизации портфельных инвестиций Первый (прямая задача Марковица) заключается в том, что налагается некоторое ограничение на степень риска – риск не
должен превышать некоторый допустимый уровень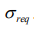
. Доходность портфеля при этом должна быть максимальной. Математическое описание модели Марковица для задачи на максимум доходности будет выглядеть:
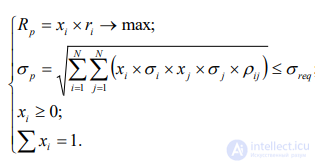(8.11)
Здесь
ix – относительная доляi-го актива в портфели банка,
ir – доходность, рассчитанная, как среднее значение доходности за исследуемый период,
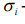рискi -го актива, рассчитанный как его стандартное отклонение за исследуемый период,
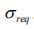- максимально допустимое значение риска, устанавливаемое экспертом,
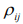– коэффициент линейной корреляции между доходностями двух видов активов. Задача (8.11) является нелинейной и не может быть решена в рамках симплекс метода.

Для решения таких задач используют методы нелинейного программирования и, в частности, возможности Microsoft Ecsel (Поиск решений).
Второй подход к решению проблемы Марковица (обратная задача Марковица) заключается в минимизации риска при сохранении некоторого гарантированного
уровня доходности Математическое описание модели Марковица для задачи на минимум риска будет выглядеть:
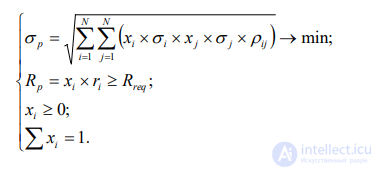(8.12)

8.4. Примеры применения модели Марковица

Пример 1. Как показано выше, при формировании портфеля ценных бумаг следует соблюдать принцип диверсификации. Согласно этому принципу к портфеля включают ценные бумаги, не коррелирующие между собой, или еще лучше – имеют отрицательную корреляцию. Рассмотрим портфель, состоящий из акций двух типов Норма прибыли портфеля рассчитывается по формуле

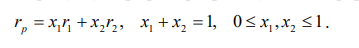. (8.13)

Здесь
i x – доля и-й ценной бумаги в структуре портфеля;
i r – ожидаемое значение прибыли акции и-го типа.

При нестационарном характере поведения цены акций ожидаемое значение прибыли часто оценивают как наклон тренда цены акций
некотором базовом участке.

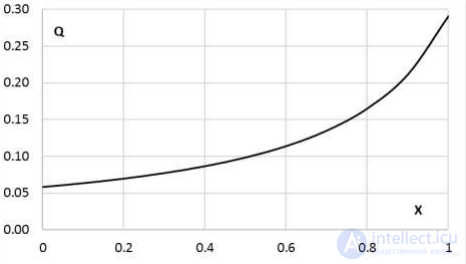
Рис. 8.1. Зависимость денежной привлекательности Q пары акций от ее формулы x.

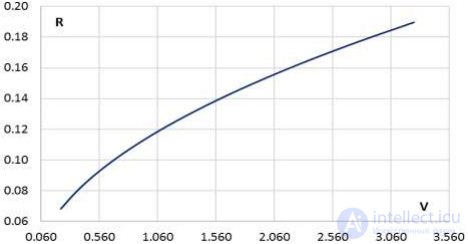
Рис. 8.2. Зависимость доходности R от риска V для пары акций
Риск портфеля по двум акциям определяется по формуле
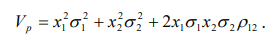. (8.14)
Здесь

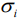- среднеквадратическое отклонение цены акции и-го типа;
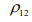- коэффициент корреляции обеих акций.

Финансовая привлекательность Q пара акций оценивается как отношение ожидаемой прибыли к риску портфеля
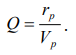. (8.15)
Задача состоит в максимизации финансовой привлекательности пары акций.

Зависимость денежной привлекательности пары акций от ее формулы представлена ​​на рис.8.1.
Зависимость доходности портфеля от его риска представлена ​​на рис. 8.2.

Как видим, более высокая доходность сопровождается большим риском.
Этот вывод можно считать общим законом экономики.

Пример 2. Модель Марковица применима к оптимизации аграрного. производства. Рассмотрим аграрное предприятие, 3 сельскохозяйственные культуры: пшеницу, сахарную свеклу и картофель. Известная статистика рентабельности этих культур за последние 10 лет. В роли прибыли будем рассматривать среднюю рентабельность культур соответственно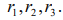
. Риск каждой культуры будем оценивать через среднеквадратичное отклонение соответствующей рентабельности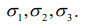

Средневзвешенная рентабельность трех культур рассчитывается по формулой
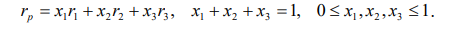. (8.16)
Здесь

xi – доля и-й культуры в общем массиве посевов;
ri – средняя рентабельность соответствующей культуры.
Риск портфеля из трех культур определяется по формуле
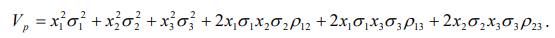. (8.17)
Здесь
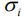- среднеквадратическое отклонение рентабельности и-й культуры;
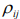– коэффициент корреляции рентабельностей двух культур.

Задача состоит в максимизации прибыли (взвешенной рентабельности) при ограниченном риске Математическая модель для сформулированной задачи аграрного производства будет выглядеть:

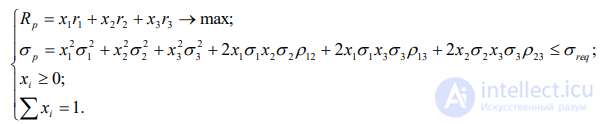(8.18)

Зависимость доходности портфеля трех культур от его риска представлена ​​на рис.8.3. Снова видим, что максимальное значение доходности связано с максимальным значением риска и наоборот.

Рис. 8.3. Зависимость доходности R от риска V для портфеля трех культур