Алгоритм упорядочения графа систем. Порядковая функция графа

Привет, Вы узнаете о том , что такое упорядочение графа, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое упорядочение графа, порядковая функция графа , настоятельно рекомендую прочитать все из категории Системный анализ (системная философия, теория систем).

В этой статье рассмотрим введение порядковой функции на ориентированном графе. Будет приведено описание алгоритма порядковой функции и его реализация на языке программирования C#.

упорядочение графа - это процесс нахождения линейного порядка вершин в графе, который удовлетворяет определенным условиям. Один из таких порядков - топологический порядок. Топологический порядок применяется к ориентированным ациклическим графам (DAG), где каждое ребро идет от вершины к вершине, и при этом не создается циклов.

Расчеты в задачах с графами заметно упрощаются, если их элементы упорядочены.

Вершина x_i предшествует вершине x_j, если существует путь из x_i в x_j (x_j называется последующей).

Под упорядочением вершин связного орграфа без контуров понимают такое разбиение его вершин на группы, при котором:

1. вершины первой группы не имеют предшествующих, а вершины последней – последующих;

2. вершины каждой другой группы не имеют предшествующих в следующей группе;

3. вершины одной группы дугами не соединяются.

Аналогично вводится понятие упорядочения дуг.

В результате получается граф, изоморфный данному.

В теории графов вполне упорядочиваемый граф — это граф, вершины которого можно упорядочить так, что алгоритм жадной раскраски с этим упорядочением оптимально раскрашивает любой порожденный подграф заданного графа. Соответствующее упорядочение называется совершенным. Вполне упорядочиваемые графы образуют подкласс совершенных графов и в это подкласс входят хордальные графы, графы сравнимости и дистанционно-наследуемые графы. Однако проверка, является ли граф вполне упорядочиваемым, есть NP-полная задача.

Описание алгоритма упорядочения графа

Целью введения порядковой функции на графе без контуров является разбиение множества вершин графа на непересекающиеся подмножества, упорядоченные таким образом, что если вершина входит в подмножество с номером i, то следующая за ней вершина — в подмножество с номером, большим i. Полученные непересекающиеся подмножества называются уровнями.

Порядковая функция на ориентированном графе без контуров разбивает множество вершин графа на непересекающиеся подмножества, упорядоченные так, что если вершина входит в подмножество с номером i, то следующая за ней вершина входит в подмножество с номером большим чем i. Полученные непересекающиеся подмножества вершин называются иерархическими уровнями.

Приведем описание алгоритма упорядочения графа:

1. В подмножество нулевого уровня N0 включаются все вершины i, в которые нельзя попасть не из какой-либо другой вершины. Об этом говорит сайт https://intellect.icu . В этом подмножестве проводится последовательная нумерация вершин 1, 2, …, m.
2. В подмножество первого уровня N1 включаются все вершины i, в которые можно попасть только из вершин уровня N0. Проводится нумерация вершин m + 1, m + 2, …, m + r.
3. В подмножество N2 включаются все вершины i, в которые можно попасть только из вершин более низких уровней и т.д. Подобная процедура продолжается до тех пор, пока не будут пронумерованы все вершины графа.

Рассмотрим пример. Пусть имеется граф, как на рисунке ниже.

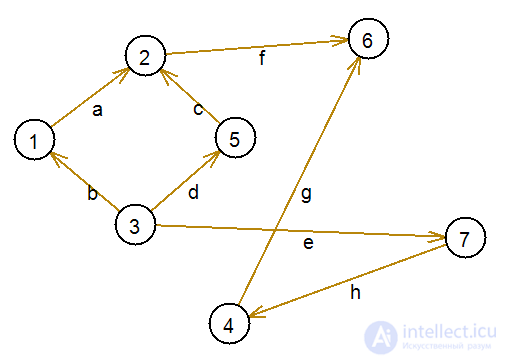
После введения порядковой функции на этом графе, получим следующее:

Реализация алгоритма

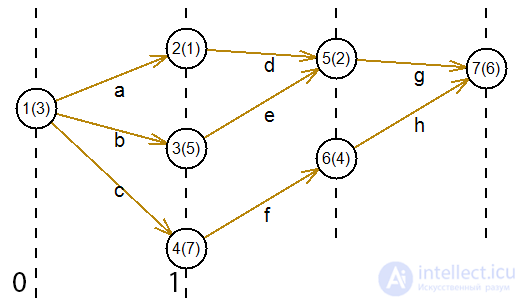
Рассмотрим реализацию алгоритма введения порядковой функции на графе. Для разработки будет использоваться язык C#.

Пусть дуга графа представляет собой экземпляр класса Edge:

public class Edge
{
public int v1, v2;
public Edge(int v1, int v2)
{
this.v1 = v1;
this.v2 = v2;
}

}

, где v1 – номер вершины, из которой дуга исходит, а v2 - номер вершины, в которую данная дуга заходит.

Иерархический уровень упорядоченного графа представим экземпляром класса HierarchicalLevel:

public class HierarchicalLevel
{
public List level;
public HierarchicalLevel()
{
level = new List();
}
}

, где level – список номеров вершин, входящих в данный иерархический уровень.

Все множество дуг и иерархических уровней упорядоченного графа будем хранить в виде соответствующих списков:

List E;
List HL = new List()

Приведем реализацию метода createHLevel(…), упорядочивающего граф.

public void createHLevel(List HL, int numberV, List E) //numberV - количество вершин
{
List usedV = new List(); //список вершин, уже использованных в порядковой функции
List notUsedV = new List(); //список вершин, еще не использованных в порядковой функции
for (int i = 0; i < numberV; i++)
notUsedV.Add(i);

while (notUsedV.Count > 0)
{
HL.Add(new HierarchicalLevel());
for (int i = 0; i < notUsedV.Count; i++)
{
int k = 0;
for (int j = 0; j < E.Count; j++)
if (E[j].v2 == notUsedV[i])
k++; //считаем полустепень захода вершины
for (int m = 0; m < usedV.Count; m++)
for (int j = 0; j < E.Count; j++)
{
if (E[j].v1 == usedV[m] && E[j].v2 == notUsedV[i])
k--; //вычитаем дуги, иходящие из вершин предыдущих уровней и входящие в вершину i
}
if (k == 0)
{
HL[HL.Count - 1].level.Add(notUsedV[i]);
notUsedV.RemoveAt(i);
i--;
}
}
for (int j = 0; j < HL[HL.Count - 1].level.Count; j++)
{
usedV.Add(HL[HL.Count - 1].level[j]);
}
}
}

Аргументы метода createHLevel: HL – список иерархических уровней графа, numberV – количество вершин в графе, E – список дуг в графе.

Кратко опишем принцип работы метода createHLevel(). В начале все вершины считаются неиспользованными и заносятся в список notUsedV. Программа продолжает работу, пока список notUsedV не окажется пустым. На каждой итерации для данного иерархического уровня перебираются все вершины из списка notUsedV. Для каждой вершины из этого списка вычисляется ее полустепень захода (int k), затем из этого числа вычитается количество дуг, входящих в вершину из вершин предыдущих уровней (эти вершины хранятся в списке usedV). Если в итоге k оказывается равным нулю, значит вершина принадлежит данному уровню: добавляем ее список вершин уровня и удаляем из списка неиспользованных вершин. В конце итерации для данного иерархического уровня обновляем список использованных вершин usedV: добавляем в него номера вершин, занесенных в данный уровень.

Примечание

Поскольку введение порядковой функции возможно только на графе без контуров, то можно сделать соответствующую проверку графа на их наличие. для этого используется алгоритм поиска циклов в неориентированном графе, немного модифицировав его, а именно, убрав обратный проход по ребру, вы получите функцию для поиска контуров в ориентированном графе.

Пример 2

Для структуры, граф которой приведен на рисунке, провести упорядочение. Построить матрицы смежности к упорядочению и после составления, выяснить, чем они отличаются.

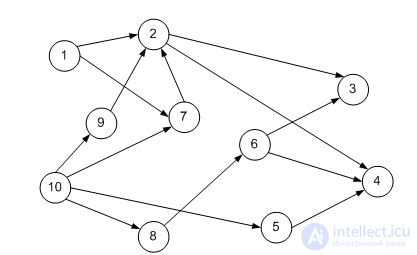
Пример решения.
Матрица смежности исходного графа:

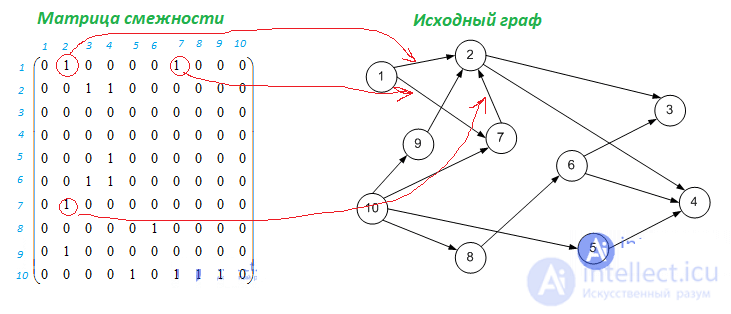
Подмножества вершин:

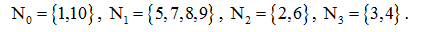
Иерархический граф, полученный из исходного:

Матрица смежности иерархического графа:

public void createHLevel(List HL, int numberV, List E) //numberV - количество вершин
{
List usedV = new List(); //список вершин, уже использованных в порядковой функции
List notUsedV = new List(); //список вершин, еще не использованных в порядковой функции
for (int i = 0; i < numberV; i++)
notUsedV.Add(i);

while (notUsedV.Count > 0)
{
HL.Add(new HierarchicalLevel());
for (int i = 0; i < notUsedV.Count; i++)
{
int k = 0;
for (int j = 0; j < E.Count; j++)
if (E[j].v2 == notUsedV[i])
k++; //считаем полустепень захода вершины
for (int m = 0; m < usedV.Count; m++)
for (int j = 0; j < E.Count; j++)
{
if (E[j].v1 == usedV[m] && E[j].v2 == notUsedV[i])
k--; //вычитаем дуги, иходящие из вершин предыдущих уровней и входящие в вершину i
}
if (k == 0)
{
HL[HL.Count - 1].level.Add(notUsedV[i]);
notUsedV.RemoveAt(i);
i--;
}
}
for (int j = 0; j < HL[HL.Count - 1].level.Count; j++)
{
usedV.Add(HL[HL.Count - 1].level[j]);
}
}
}

Вау!! 😲 Ты еще не читал? Это зря!

• граф
• марица инцедентности

В заключение, эта статья об упорядочение графа подчеркивает важность того что вы тут, расширяете ваше сознание, знания, навыки и умения. Надеюсь, что теперь ты понял что такое упорядочение графа, порядковая функция графа и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Системный анализ (системная философия, теория систем)