Алгоритмы выделения контуров для комлексов графа

Привет, Вы узнаете о том , что такое алгоритмы выделения контуров для комлексов графа, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое алгоритмы выделения контуров для комлексов графа , настоятельно рекомендую прочитать все из категории Системный анализ (системная философия, теория систем).

рис 3 Определение ППРС.

Для рассмотренной  системы имеем : ППРС - [ 7, ( 1, 2. 3, 8, 9, 10 ), 4, ( 5, 11 ), 6 ]

Выделение контуров производится отдельно для каждого комплекса. Один из способов выделения контуров заключается в построении прадерева комплекса. Прадеревом комплекса с корнем К, называют такое изображение всех путей, существующих в комплексе, когда в каждую вершину, отличную от К, входит только одна дуга. В вершину К прадерева ни одна дуга не входит. Построение каждого пути продолжают до тех пор, пока на нем не встретятся повторяющиеся вершины. В этом случае построение соответствующего пути заканчивают, а последнюю вершину называют висячей вершиной прадерева..

Выделение контуров целесообразно проводить в следующей последователь­ности:

Представляют структуру каждого комплекса, например в виде спис­ка связи. В качестве примера приводится список связи комплекса ( 1, 2, 3, 8, 9. 10 ), входящего в состав ХТС, представленной на рис. 3.

 Производят построение прадерева комплекса. Для построения прадерева из любой вершины комплекса, которую принимают за корень прадерева, строят все пути, существующие в комплексе. Каждую ветвь сnроят до тех пор, пока на ней не встретится уже имеющаяся -вершина (висячая вершина ).

Участки ветвей прадерева между повторяющимися вершинами являются кон­турами, входящими в состав комплекса. Каждой висячей вершине соответству­ет контур.

На рис. 5 показано прадерево комплекса ( 1, 2, 3, 8,9, 10 )( см. выше со­ответствующий список связи).

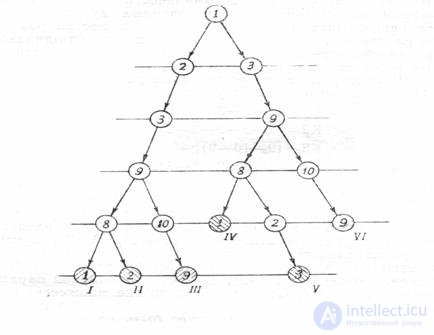
Рис. 4.  Выделение контуров комплекса (1.2.3.8.9.10).

Римскими цифрами отмечены висячие вершины праперева.

            Выделенные контуры заносят в таблицу контуров. Ниже приведены кон­туры, входящие в состав рассматриваемого комплекса.

Таблица 1 . Контуры, входящие в состав комплекса (1, 2, 3, 8, 9,10)

Как видно из табл. 1, общее число висячих вершин прадерева больше чис­ла различных контуров, так как различные висячие вершины могут отвечать одному и тому же контуру. Об этом говорит сайт https://intellect.icu . В рассматриваемом комплексе висячим вершинам 1 и IV соответствуют одинаковые контуры 9-10-9 и вершинам III и VI одина­ковые контуры 2- 3-9-8-2 и 3- 9- 8- 2- 3.

Для дальнейшей работы из двух или нескольких одинаковых контуров в таб­лице контуров оставляют только один.

То, что одни и те же контуры выделяются иногда несколько раз, является недостатком рассмотренного алгоритма.

Алгоритмы определения оптимального множества разрываемых потоков.

С  точки зрения трудоемкости и точности расчетов небезразлично, в ка­ких местах производить разрыв  связей комплекса. Для того чтобы режим в разомкнутой ХТС соответствовал режиму в комплексе, необходимо выполне­ние условия равенства параметров потока после места разрыва соответствую­щим параметрам до места разрыва. Можно показать, что данное условие при­водит к необходимости решения системы нелинейных уравнений, суммарный порядок которой равен сумме параметричностей разрываемых дуг ( параметричносmь или размерность дуги - это число параметров, характеризующих соот­ветствующий технологический поток ).

При выборе мест разрывов в качестве критерия оптимальности может использоваться суммарная параметричность разрываемых дуг, т. е. сумма неиз­вестных параметров потоков в местах разрыва.

Для отыскания оптимально-раэрнвающего множества дуг строится матрица входящих в комплекс контуров, в  которой группируется необходимая инфор­мация для решения рассматриваемой задачи. Элементы матрицы контуров К (I,J) (1- номер контура, J- номер дуги) определяется по следующему правилу:

. Матрица  контуров  комплекса ( !, 2, 3, 8, 9, 10 ) имеет вид:

Определим теперь контурную степень J-й дуги f(J): она равна числу контров, в которые входит данная дуга, т. е. числу единиц, стоящих под дугой J.  Чем больше контурная степень дуги, тем больше будет разомкнуто контуров при ее разрыве. Если f(I)= f(J), причем 1-я и J-я дуги входят в одни и те же контуры, то предпочтительнее разрывать дугу с меньшей параметричностью р. В нашем примере параметричности дуг выбраны условно.

При отыскании оптимального множества разрываемых дуг нужно учиты­вать следующие правила:

1. Количество мест разрывов должно быть выбрано так, чтобы были ра­зорваны все контуры комплекса.

2. Если параметричность всех дуг одинакова, задача сводится к определе­нию минимального числа дуг, разрыв которых превращает комплекс в разо­мкнутую подсистему. В этом случае следует найти дугу, имеющую максималь­ную контурную степень. В нашем примере максимальное значение f имеет ду­га 3-9 или 9-8. Разрыв любой из этих дуг приведет к уменьшению числа контуров в комплексе (у нас контуры К2, КЗ и К4 окажутся разомкнутыми ). Из матрицы контуров вычеркнем эти контуры и вновь пересчитаем контурные степени оставшихся дуг. Вновь разыскиваем среди этих дуг дугу, имеющую максимальную контурную степень, и исключаем соответствующие контуры. Этот процесс продолжают до тех пор, пока не останется контуров,

В нашем примере все контуры могут быть разомкнуты после разрыва двух дуг 3-9 и 9-10 или 9-8 и 10-9, что свидетельствует о том, что решение задачи может быть не единственным.

3. В общем случае, когда параметричность дуг комплекса различна, разры­ваемые дуги выбираются так, чтобы их суммарная параметричность была ми­нимальной. Для определения наиболее выгодных мест разрыва в этом случае необходимо найти всевозможные варианты разрываемых дуг (с учетом правила 1), определить суммарные параметричности различных вариантов и найти среди этих параметричностей минимальную. Множество разрываемых дуг с  минимальной суммарной параметричностью и будет оптимальным.

Для рассматриваемого примера в табл. 2 представлены различные варианты множеств разрываемых дуг.

Таблица 2.  Варианты множеств разрываемых дуг комплекса (1, 2,3,8,9, 10)

Как видно из таблицы, минимальную суммарную параметричность имеет множество дуг ( 2-3, 8-1, 9-10 ). Именно эти дуги следует разрывать для пре­вращения комплекса в разомкнутую ХТС в рассматриваемом примере.

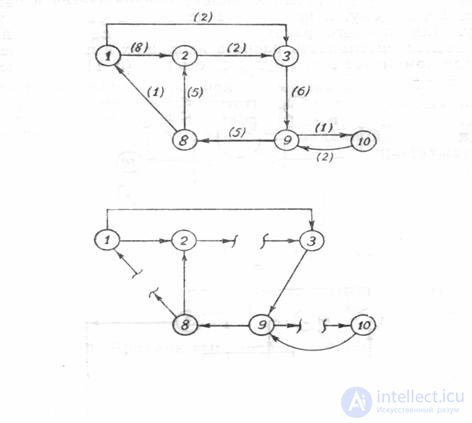
Рис. 5.  Комплекс с дугами разной параметричностм и соответствующая ему

разомкнутая ХТС.

Выводы из данной статьи про алгоритмы выделения контуров для комлексов графа указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое алгоритмы выделения контуров для комлексов графа и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Системный анализ (системная философия, теория систем)