Лекция
Привет, Вы узнаете о том , что такое построение фракталов дробная размерность, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое построение фракталов дробная размерность , настоятельно рекомендую прочитать все из категории Синергетика.
Рассмотрим т.н. множество Кантора и ковер Серпиньского. Эти множества обладают геометрической инвариантностью и известны как "множества средних третей". Отрезок единичной длины [0, 1] делится на три равные части, и средняя из них - интервал (1/3, 2/3) - вырезается. С каждым из остальных отрезков поступают точно так же (рис. 1).
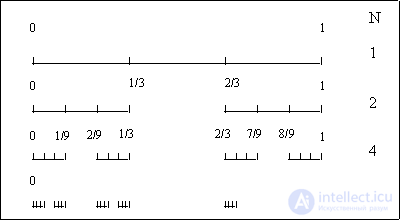
Получаем последовательность отрезков все убывающей длины. На первом этапе имеем один отрезок, на втором - два, на третьем - четыре, на к-ом - 2kотрезков, длиной 3-k каждый. При k 
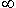 получим множество точек, которое называется множеством Кантора. Суммарная длина всех вырезанных отрезков при этом равна единице.
получим множество точек, которое называется множеством Кантора. Суммарная длина всех вырезанных отрезков при этом равна единице.
 .
.Обобщение канторова множества средних третей на случай плоских фигур приводит к ковру Серпиньского.

Возьмем квадрат со стороной, равной единице, и разделим его на девять равных квадратов; при первой итерации (к=1) удаляем центральный квадрат; аналогично поступим с каждым из оставшихся восьми квадратов (к=2) и т. д. (рис. 2). Пересечение полученных при k 
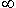 множеств - это ковер Серпиньского. Канторово множество, грубо говоря, является как бы "всюду дырявым".
множеств - это ковер Серпиньского. Канторово множество, грубо говоря, является как бы "всюду дырявым".
Существует важная количественная характеристика канторова множества - дробная размерность. Рассмотрим некоторое множество А и попытаемся полностью покрыть его отрезками, квадратиками или гиперкубами со стороной 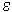 (рис. Об этом говорит сайт https://intellect.icu . 3). Пусть N - минимальное число кубиков или квадратиков, необходимых для покрытия А. Рассмотрим предел
(рис. Об этом говорит сайт https://intellect.icu . 3). Пусть N - минимальное число кубиков или квадратиков, необходимых для покрытия А. Рассмотрим предел
 . (1)
. (1)Величина d(А)=dF является метрической размерностью и называется фрактальной размерностью.

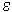 :
:Найдем фрактальную размерность квадрата со стороной 1. Для того чтобы закрыть этот квадрат необходимо иметь (1/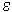 )2 квадратов со стороной
)2 квадратов со стороной 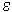 . Следовательно, d равно
. Следовательно, d равно
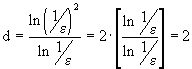 ,
,Найдем d для множества Кантора (рис. 1). При первом разбиении для покрытия необходимо иметь два отрезка длиной 1/3; при втором разбиении потребуется четыре отрезка длиной 1/9 и вообще при n-ом разбиении нужно иметь 2n отрезков длиной (1/3)n. Итак, множество Кантора состоит из N=2n разделенных интервалов длиной (1/3)n каждый. Использовав определение (1), получим
 .
.Таким образом, множество Кантора - промежуточное между точкой (d=0) и линией (d=1), т. е. оно является фракталом.
Определим фрактальную размерность ковра Серпиньского. Имеем при первом (к=1) и последующих разбиениях
| k=1 | N=8=8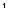 |
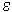 =(1/3) =(1/3)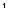 |
| k=2 | N=8*8=8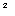 |
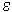 =(1/3) =(1/3)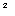 |
| k=3 | N=8*8*8=8 |
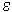 =(1/3) =(1/3) |
| k=n | N=8n | 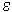 =(1/3)n =(1/3)n |

Следовательно, ковер Серпиньского - это уже не линия с размерностью 1, но еще и не поверхность, размерность которой 2. Это что-то между линией и поверхностью. Самым неожиданным является то, что в природе существуют объекты, представляющие аналог ковра Серпиньского с размерностью 1<d<2. Это фрактальные агрегаты коллоидных частиц.
Рассмотрим теперь другой классический фрактальный объект - снежинку. Снежинка имеет бесконечный периметр, хотя ограничивает конечную область плоскости. Возьмем равносторонний треугольник, разделим каждую из его сторон на три части и по каждой из трех центральных третей построим по равностороннему треугольнику меньших размеров. Итерируя это построение бесконечно много раз, получим фрактальный объект, называемый иногда кривой Коха, размерность которого d = ln4/ln3 ~ 1,26 (рис.4).

Аналогичным способом можно построить много различных фракталов. Приведем некоторые из них.




Прочтение данной статьи про построение фракталов дробная размерность позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое построение фракталов дробная размерность и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Синергетика
Из статьи мы узнали кратко, но содержательно про построение фракталов дробная размерность
Комментарии
Оставить комментарий
Синергетика
Термины: Синергетика