Лекция
Привет, Вы узнаете о том , что такое машина гельмгольца, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое машина гельмгольца, алгоритм бодрствования-сна , настоятельно рекомендую прочитать все из категории Вычислительный интеллект.
Машина Гельмгольца (названная в честь Германа фон Гельмгольца и его концепции свободной энергии Гельмгольца ) представляет собой тип искусственной нейронной сети, которая может учитывать скрытую структуру набора данных путем обучения созданию генеративной модели исходного набора данных. . Есть надежда, что, изучая экономические представления данных, основная структура генеративной модели должна разумно аппроксимировать скрытую структуру набора данных. машина гельмгольца содержит две сети, восходящее распознавание сеть, которая принимает данные в качестве входных данных и производит распределение по скрытым переменным, и нисходящую «генерирующую» сеть, которая генерирует значения скрытых переменных и самих данных.
Машины Гельмгольца обычно обучаются с использованием алгоритма обучения без учителя , такого как алгоритм бодрствования-сна . Они являются предшественниками вариационных автокодировщиков , которые вместо этого обучаются с использованием обратного распространения ошибки . Машины Гельмгольца также могут использоваться в приложениях, требующих контролируемого алгоритма обучения (например, распознавание символов или позиционно-инвариантное распознавание объекта в поле).
Эти сети очень разные по архитектуре и по способу обучения.
Машина Гельмгольца содержит две сети: восходящую сеть распознавания, которая принимает данные в качестве входных данных и производит распределение по скрытым переменным, и нисходящую «генерирующую» сеть, которая генерирует значения скрытых переменных и самих данных.
Машины Больцмана намного проще, и их единицы просто разделены на «видимые» единицы, V, и «скрытые» единицы, H. Видимые единицы - это те, которые получают информацию из «окружающей среды», т.е. наш обучающий набор представляет собой набор двоичных векторов над множеством V.
Машины Гельмгольца были созданы для повышения устойчивости к шуму, которая всегда присутствует в естественных данных, и в надежде, что, изучая экономичное представление данных, основная структура генеративной модели должна разумно аппроксимировать скрытую структуру набора данных.
Две фазы машины Больцмана противопоставляют статистику активаций сети, когда шаблоны ввода представлены, со статистикой активаций сети, когда она работает «бесплатно». Эта контрастная процедура связана со значительным шумом и поэтому выполняется медленно.
Машины Гельмгольца обучаются с использованием так называемого алгоритма «бодрствования-сна» ( http://www.gatsby.ucl.ac.uk/~dayan/papers/d2000a.pdf ), в котором фазы бодрствования и сна не контрастируют. Скорее, модели распознавания и генерации вынуждены преследовать друг друга.
Машина Гельмгольца также имеет интересную связь с машиной Больца-Манна, которую можно рассматривать как ненаправленную сеть убеждений.
Кроме того, правило машинного обучения Больцмана выполняет истинный стохастический градиентный подъем логарифмической вероятности с использованием контрастной процедуры, которая, что сбивает с толку, включает фазы бодрствования и сна, которые сильно отличаются от фаз бодрствования и сна алгоритма бодрствования-сна.
Подводя итог, можно сказать, что эти модели связаны таким образом, что обе используют репрезентативное обучение, но для многих проблем машины Гельмгольца просто предоставляют удобные аппроксимации.
Растущее количество поведенческих и нейрофизиологических данных свидетельствует о том, что мозг выполняет оптимальные (или почти оптимальные) вероятностные выводы и обучение во время восприятия и других задач. Хотя существует множество алгоритмов машинного обучения, которые выполняют логический вывод и обучение оптимальным образом, полное описание того, как один из этих алгоритмов (или новый алгоритм) может быть реализован в мозге, в настоящее время является неполным. Было предложено множество решений, касающихся того, как нейроны могут выполнять оптимальный вывод, но вопрос о том, как синаптическая пластичность может реализовать оптимальное обучение, редко рассматривается. Эта статья направлена на объединение двух областей вероятностного вывода и синаптической пластичности с помощью нейронной сети реалистичных моделей нейронов с импульсами для реализации хорошо изученной вычислительной модели, называемой машиной Гельмгольца. Машина Гельмгольца поддается нейронной реализации, поскольку алгоритм, который она использует для изучения своих параметров, называемый алгоритмом бодрствования-сна, использует локальное правило дельта-обучения. Наша сеть с пиковыми нейронами реализует как правило дельты, так и небольшой пример машины Гельмгольца. Эта нейронная сеть может изучать внутреннюю модель непрерывных наборов обучающих данных без присмотра. Сеть также может выполнять логический вывод по изученным внутренним моделям. Мы показываем, как различные биофизические особенности нейронной реализации ограничивают параметры алгоритма бодрствования-сна, такие как продолжительность фаз обучения бодрствования и сна и минимальная продолжительность выборки. Мы исследуем отклонения от оптимальной производительности и связываем их со свойствами правила синаптической пластичности.
Люди и другие животные живут в предсказуемой и структурированной среде, где они должны принимать быстрые и эффективные решения, чтобы добыть пищу, спастись от хищников и найти себе пару. Однако эти сенсорные входы предоставляют лишь ограниченный и часто искаженный снимок окружающей среды вокруг животного. Хотя решения принимаются с использованием этой несовершенной информации, они должны отражать реальный характер окружающей среды, поскольку именно она определяет эффект от действий животного.
Байесовский вывод дает математическое описание того, как принимать оптимальные решения с учетом этой ограниченной и искаженной информации об окружающей среде ( Bishop, 2006 ; Griffiths et al., 2010 ). Существует множество экспериментальных данных, показывающих, что люди и другие животные ведут себя в соответствии с байесовским выводом в вероятностных задачах, таких как комбинация сигналов ( van Beers et al., 1999 ; Atkins et al., 2001 ; Ernst and Banks, 2002 ; Alais and Burr, 2004 ; Burge et al., 2010 ), сочетание неуверенных доказательств с предшествующими знаниями ( Tassinari et al., 2006 ), сенсомоторное обучение ( Körding and Wolpert, 2004).), иллюзии движения ( Weiss et al., 2002 ) и причинно-следственные связи ( Blaisdell et al., 2006 ). Также наблюдается оптимальное обучение на протяжении всей жизни ( Griffiths and Tenenbaum, 2006 ) и экспериментальное ( Orbán et al., 2008 ; Chalk et al., 2010 ). Анализ нейронных записей во время восприятия естественных сцен на протяжении всего развития также в целом согласуется с оптимальным выводом ( Berkes et al., 2011 ). Это свидетельство мотивирует поиск реализации байесовского вывода в мозге.
В этой структуре мозг поддерживает вероятностную модель физических законов, которые переводят состав окружающей среды (например, объекты, которые находятся перед животным) в (искаженную) сенсорную информацию, которая поступает в мозг (рис. 1A , внизу). . Как первоначально было предложено Гельмгольцем (1925), мозг затем инвертирует эту вероятностную модель, также называемую генеративной моделью, для создания модели распознавания, которая преобразует эту искаженную информацию в оптимальную оценку состава окружающей среды, в которой мозг может затем принимать решения. около (Рисунок 1А, Вверх). Обучение в этой структуре включает в себя настройку параметров генеративной модели (и, следовательно, ее обратной модели, модели распознавания), чтобы они соответствовали статистике среды. Поскольку точный байесовский вывод обычно неразрешим ( Bishop, 2006 ), часто требуется приблизительная модель распознавания. Это приближение проявится в поведении животного в виде определенных поведенческих предубеждений ( Sanborn et al., 2010 ).
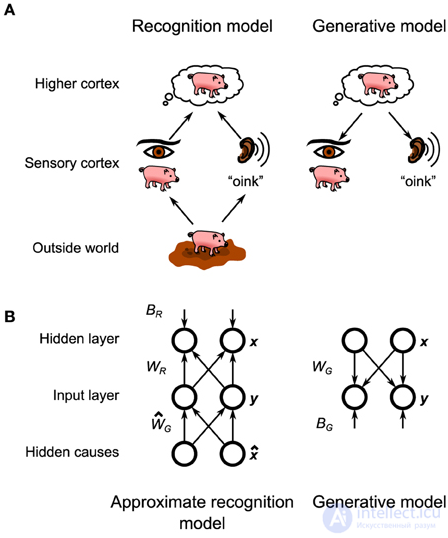
Мы заинтересованы в изучении байесовского вывода на уровне нейронной реализации. Это дает два преимущества. Во-первых, нейронный субстрат добавляет дополнительный уровень приближения и смещения, который может помочь в интерпретации поведенческих данных, как указано выше. Во-вторых, нейронная спецификация алгоритма будет определять тип данных, которые следует искать в нейронных записях. Было несколько предложений о том, как реализовать байесовский вывод в нейронных сетях ( Lee, 2002 ; Friston and Kiebel, 2009 ; Moran et al., 2013 ), и некоторые из них продвинулись к использованию импульсных нейронов ( Rao, 2005 ; Ma et al., 2006 , 2008 ; Ши и Гриффитс, 2009 ;Buesing et al., 2011 ; Pecevski et al., 2011 ). Большинство этих прошлых попыток не касались вопроса обучения. Совсем недавно появились предложения по реализации как логического вывода, так и обучения в модельных нейронах со стохастическим ( Brea et al., 2011 ; Rezende et al., 2011 ; Nessler et al., 2013 ) и детерминированным ( Deneve, 2008a , b ) механизмом пиков. были разработаны. Мы предлагаем альтернативную формулировку (подробно описанную ниже), основанную на нейронах с детерминированной динамикой с требуемой стохастичностью, происходящей от стохастического высвобождения в синаптических пузырьках.
Генеративная модель, которую мы будем реализовывать и использовать для моделирования (смоделированных) наблюдаемых данных, представляет собой смешанную модель усеченных гауссианцев:
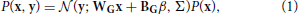
где x - активность единиц в скрытом слое, а y - активность единиц в наблюдаемом слое. Усеченный гауссовский вид задается следующей функцией распределения вероятностей:

для некоторого среднего ц, ковариационной матрицы Е и нормализующего коэффициента Z .  ( z ) - многомерная функция Хевисайда:
( z ) - многомерная функция Хевисайда:

где H (·) - обычная функция Хевисайда (с H (0) = 1), а произведение берется по всем компонентам z .
Цель восприятия, сформулированная в байесовской структуре, состоит в том, чтобы инвертировать эту генеративную модель, т. Е. Найти P ( x | y ). В общем случае это неразрешимо, поэтому используется приближенная модель распознавания. В этом случае приближенная модель распознавания также представляет собой смесь усеченных гауссиан:
Обе модели имеют фиксированную активность систематической ошибки β и матрицу дисперсии Σ . Остальные параметры, а именно генеративные веса W G , смещения B G , веса распознавания W R и смещения B Rизучаются моделью с использованием алгоритма бодрствования-сна. Значения фиксированных параметров, а также начальные значения изученных параметров подробно описаны в Таблице S1. Поскольку параметры дисперсии не изучены, точная функциональная форма компонентов смеси не имеет существенного значения (например, распределение Пуассона привело бы к идентичной нейронной реализации), пока его среднее значение линейно зависит от весов и смещений. Мы выбрали усеченный гауссовский язык для математического удобства.
Можно вывести точные правила обучения бодрствованию и сну для усеченных гауссовских единиц, следуя стандартной процедуре (см. Дополнительную информацию). Во время фазы пробуждения алгоритма генеративная модель адаптируется к среде, сначала оценивая активность скрытого слоя x ( n ) с учетом наблюдения y ( n ) из среды, используя приближенную модель распознавания, а затем корректируя генеративные веса и смещения как следует:
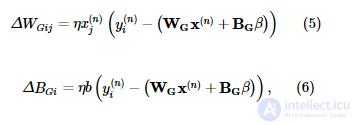
где η - скорость обучения. Во время фазы сна приближенная модель распознавания адаптируется, чтобы лучше инвертировать генеративную модель, сначала генерируя выборку { x ( n ) , y ( n ) } из генеративной модели, а затем корректируя веса распознавания и смещения:
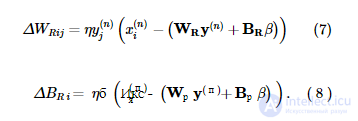
Во время обучения мы ограничиваем B R и B G положительными значениями, в то время как W G и W R не ограничиваются.
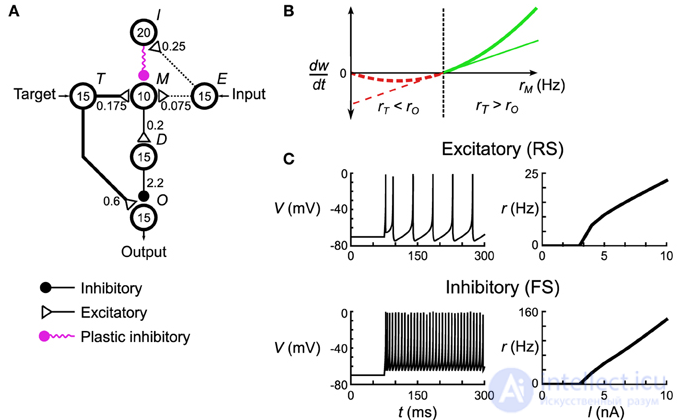
Наша модель нейронной сети будет реализовывать вышеупомянутые правила обучения, аппроксимируя их, используя биологически правдоподобные правила синаптической пластичности (рисунок 2 ). Чтобы сфокусировать наш анализ на различии между вычислительной реализацией и реализацией с использованием нейронной подложки, мы также используем приближенное правило обучения в вычислительной модели (т. Е. Мы не используем уравнения 5–8). Учитывая целевую активность T , входную активность I и выходную активность O , пусть сигнал ошибки будет M = max ( T - O , −θ). Затем вес регулируется следующим образом:
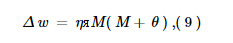
где θ - некоторая пороговая активность. Уравнения (5, 6), например, аппроксимируются формулой
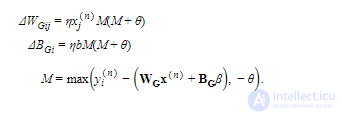
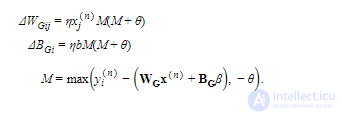
Это приближение может быть получено, если предположить, что единичная активность кодируется с использованием цепочек шипов Пуассона и что веса связей регулируются с использованием реалистичных правил синаптической пластичности (см. Дополнительную информацию). Качество этого приближения проверено эмпирически.
Для моделирования нейронов с импульсами мы используем двухвариантную модель нейронов с импульсами, предложенную Ижикевичем (2003) . Модель описывается двумя связанными обыкновенными дифференциальными уравнениями и одним пороговым условием:
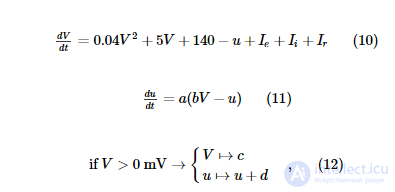
где V - мембранный потенциал (измеряется в мВ), u - ток адаптации, a , b , c , d - параметры, определяющие динамику нервного возбуждения. Мы используем два набора параметров для моделирования возбуждающих (регулярные импульсы - RS) нейронов и тормозных (быстрые импульсы - FS) нейронов (таблица S2).
I e моделирует возбуждающий ток, протекающий через рецепторы AMPA и NMDA:
где g e 1 и g e 2 - суммарные динамические проводимости (измеренные в нСм) всех возбуждающих синапсов на нейрон. NMDA ( V ) описывает зависимость тока NMDA от мембранного потенциала ( Jahr and Stevens, 1990 ):
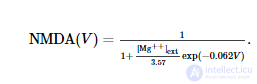
I i моделирует тормозной ток, протекающий по каналам GABA A :
где g i - суммарная динамическая проводимость (измеренная в нСм) всех тормозных синапсов на нейрон.
I r - это ток, исходящий от возбуждающих синапсов (моделируемых как токи AMPA), которые являются внешними по отношению к сети:
где g r - динамическая проводимость (измеренная в нСм) этих внешних синапсов.
Каждый раз, когда срабатывает невнешний пресинаптический нейрон, после определенной задержки Δ, проводимость соответствующего типа синапса регулируется на случайную величину:
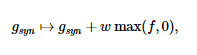
Внешние синапсы моделируются как процесс Пуассона с частотой r r Гц. Когда срабатывает внешний «нейрон», проводимость g r регулируется на фиксированную величину w r .
Между пиками все вышеупомянутые проводимости развиваются как обычные дифференциальные уравнения первого порядка:
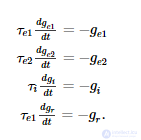
Сети дельта-правил подразделяются на однородные пулы нейронов, обозначенные метками (таблица S3, рисунок 2 ). Каждая сеть имеет входной пул E , выходной пул O и целевой пул T, которые используются для предоставления входных данных и считывания выходных данных из сети. Дополнительно есть промежуточные бассейны M и Dиспользуется сетью для выполнения вычислений и обучения (см. Результаты). Пары нейронных пулов связаны направленными разреженными связями (Таблица S4). Каждый нейрон в исходном пуле связан с той же долей нейронов в целевом пуле. Общая проводимость синапсов, создаваемых пресинаптическим нейроном, является фиксированной, и каждый синапс получает равную часть от этой суммы. Соединение разреженность, S , одинакова для всех соединений между бассейном.
Правило синаптической пластичности Spiking BCM оценивает скорость постсинаптических спайков. рˆр^post (измеряется в Гц) путем фильтрации последовательности постсинаптических спайков с использованием экспоненциального ядра:
где t j - время j -го постсинаптического всплеска. Во время каждого пресинаптического события (которое происходит в момент времени t i для i -го пресинаптического всплеска) синаптический вес регулируется следующим образом:

Правило синаптической пластичности STDPi вычисляет оценку как скорости пресинаптических спайков, рˆр^частота пре- и постсинаптических всплесковрˆр^post (оба измеряются в Гц) путем фильтрации пре- и постсинаптических последовательностей спайков соответственно с использованием ядра разности экспонент:

где t i - время i -го пресинаптического всплеска, а t j - время j -го постсинаптического всплеска. Во время каждого пресинаптического события синаптический вес регулируется следующим образом:
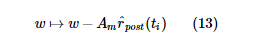
Во время каждого постсинаптического события синаптический вес регулируется следующим образом:
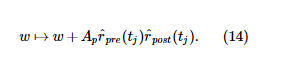
Пластиковые веса должны быть неотрицательными.
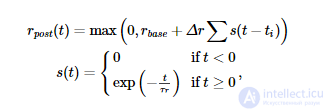
где t i - время i -го пресинаптического спайка. При построении мы используем r post , которое является средним за время r post ( t ). Мы изменяем базу r для создания необходимого r сообщения . Эти параметры перечислены в Таблице S1.
Чтобы установить целевую скорость и скорость ввода, мы изменяем r r для нейронов внутри пулов T и E соответственно. Мы поддерживаем постоянную скорость на протяжении всего периода обучения и тестирования. Выходная скорость вычисляется путем усреднения скорости активации всех нейронов внутри выходного пула O во время тестирования. В течение периода испытаний пластичность отключают (например, устанавливая соответствующие амплитуды изменения пластичности равными 0).
продолжение следует...
Данная статья про машина гельмгольца подтверждают значимость применения современных методик для изучения данных проблем. Надеюсь, что теперь ты понял что такое машина гельмгольца, алгоритм бодрствования-сна и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Вычислительный интеллект
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Вычислительный интеллект
Термины: Вычислительный интеллект