Лекция
Это продолжение увлекательной статьи про машина гельмгольца.
...
подключение
Реализация машины Гельмгольца в нейронной сети состоит из четырех блоков, расположенных на двух уровнях. Эти единицы точно соответствуют единицам x и y вычислительной модели . Каждый модуль имеет ту же возможность подключения, что и сеть дельта-правил, за исключением того, что пул E удаляется, а пул R и добавляются переменные, помеченные выходными пулами X 1 , X 2 , Y 1 , Y 2 (таблица S3). Дополнительно пул Iтеперь связан с исходным пулом, а не с целевым пулом (хотя возможности подключения такие же). Эти субъединицы связаны между собой путем создания возбуждающих проекций из выходного пула и тормозящих проекций из пула I устройства на одном слое в пул M элемента в другом слое (Таблица S4).
Входы в сеть приходят полностью через настройку т г переменного пул Т к Г Т . Во время фазы пробуждения r T устанавливается равным y ( n ) 1 и y ( n ) 2 для блоков y 1 и y 2 и равным r ns для блоков x 1 и x 2 . Во время фазы сна происходит обратное: r T устанавливается на x ( n )1 и x ( n ) 2 для блоков x 1 и x 2 и до r ns для блоков y 1 и y 2 . Кроме того, связь между блоками изменяется между фазами, как подробно описано в Таблице S4.
Распределения вероятностей по выходным скоростям вычисляются путем вычисления гистограммы выборок, собранных из сети. Выборка вычисляется путем усреднения скорости всех нейронов в соответствующем выходном пуле за длительность выборки, T выборка .
Генеративные тесты и тест вознаграждения используют приоры, происходящие от двух семейств унимодальных и бимодальных приоров:

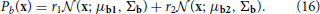
Параметры, использованные для этих предыдущих распределений, перечислены в Таблице S5.
В тесте декодирования используется предшествующая единообразная строка:

где 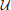 ( z ; a , b ) - это выборка равномерного распределения z из [ a , b ], а δ (·, ·) - символ Кронекера. Об этом говорит сайт https://intellect.icu . При построении мы собираем N тестовых выборок из каждого распределения.
( z ; a , b ) - это выборка равномерного распределения z из [ a , b ], а δ (·, ·) - символ Кронекера. Об этом говорит сайт https://intellect.icu . При построении мы собираем N тестовых выборок из каждого распределения.
Вычислительная модель и нейронная сеть обучаются на наборе из 10 наборов данных, причем первые восемь используются для тестов генеративной модели, а последние два - для теста декодирования и теста вознаграждения соответственно. Наборы данных генерируются перед обучением (и повторно используются для всех моделей) путем извлечения N тестовых выборок из распределений вероятностей. Мы выбрали тренировочные распределения таким образом, чтобы они избегали низких скоростей стрельбы, где наши правила обучения имеют наибольшую неточность.
Во время обучения точки данных берутся последовательно и в одном и том же порядке для всех испытаний (перезапуск с начала, когда набор данных исчерпан). Унимодальные наборы данных a … e взяты из усеченного гауссовского распределения:

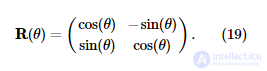
Наборы бимодальных данных f … i взяты из смеси двух усеченных гауссиан:
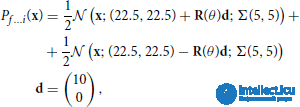
где Σ (ρ 1 , ρ 2 ) и R (θ) определены в уравнениях (18, 19). Параметры для этих распределений подробно описаны в Таблице S6.
Набор данных o для задачи декодирования извлекается из однородного линейного распределения с добавленным усеченным гауссовым шумом:
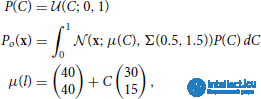
где 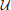 ( z ; a , b ) - выборка z равномерного распределения из [ a , b ], а Σ (ρ 1 , ρ 2 ) определена в уравнении (18). Точки данных помечены значением переменной C, использованной для их создания.
( z ; a , b ) - выборка z равномерного распределения из [ a , b ], а Σ (ρ 1 , ρ 2 ) определена в уравнении (18). Точки данных помечены значением переменной C, использованной для их создания.
Набор данных r для задачи вознаграждения взят из однородного линейного распределения:

где δ (·, ·) - символ Кронекера. Точки данных помечены значением переменной C, которая использовалась для их создания.
Мы вычисляем сходство между двумя вероятностными распределениями P ( x ) и Q ( x ), используя расхождение Дженсена-Шеннона ( Lin, 1991 ):
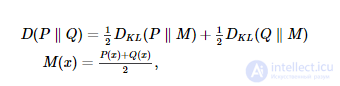
где D KL - расходимость Кульбака – Лейблера ( Кульбак, Лейблер, 1951 ):

Мы используем основание 2 для логарифма, так что D находится в диапазоне от 0 до 1. Поскольку в большинстве случаев у нас нет доступа к полному распределению вероятностей, мы оцениваем D , вычисляя его между двумя двумерными гистограммами. Гистограммы представляют собой 40 интервалов с каждой стороны (всего 1600 интервалов) и находятся в диапазоне от 0 Гц до 60 Гц. Этот метод вычисления D необъективен ( Treves and Panzeri, 1995 ), но он достаточно точен для целей данной статьи.
Учитывая выборку x ( n ) из вычислительной модели или из нейронной сети, мы декодируем представленное значениеCˆ( п )C^(п) проецируя этот образец на линию, образованную предыдущим:
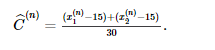
Затем мы можем вычислить среднее отклонение следующим образом:
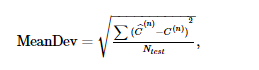
где C ( n ) - это метка, связанная с y ( n ), которая была взята из набора данных и сгенерировала x ( n ) .
Расшифровываем представленное значение  используя метод, аналогичный методу теста декодирования (за исключением другого предшествующего):
используя метод, аналогичный методу теста декодирования (за исключением другого предшествующего):
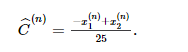
Затем мы вычисляем вероятность ответа, 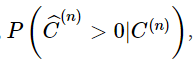 модели и дополнить ее логистической функцией:
модели и дополнить ее логистической функцией:
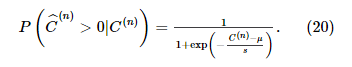
Мы интерпретируем μ как порог принятия решения, а s как меру внутреннего шума системы.
Мы вычисляем вознаграждение, полученное моделью, следующим образом:
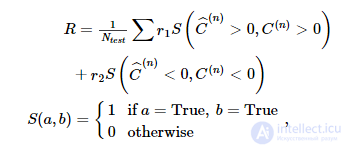
где r 1 и r 2 - награды, связанные с двумя вариантами. Поскольку в машине Гельмгольца существует симметрия, мы меняем местами x 1 и x 2, чтобы переключить интерпретацию всех испытаний, если такой переворот увеличивает вычисленное вознаграждение.
Если мы предположим, что системный шум распределен как логистическое распределение, то с учетом порога принятия решения μ и внутреннего масштаба системного шума s награда, достигаемая зашумленным декодером, составляет:
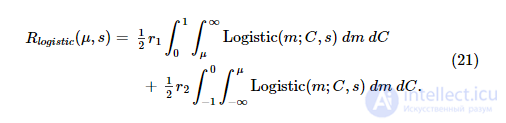
Оптимальный порог μ opt получается путем максимизации логистики R :

где масштаб шума оценивается по модели для испытаний, где r 1 = r 2 . Минимальное вознаграждение, которое может быть получено с учетом нашей методологии подсчета очков, составляет:
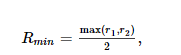
которое также можно получить, вычислив соответствующий предел уравнения (21).
Эта задача особенно подвержена проблемам сходимости, поэтому мы отказались от моделей, у которых пороги принятия решения выходили за пределы диапазона [ Q 1 - 1,5 IQR , Q 3 + 1,5 IQR ], где Q 1 и Q 3 являются первым и третьим квартилями, а IQR = Q 3. - Вопрос 1.
Вычислительная модель была смоделирована с использованием специального кода, написанного на языке программирования D ( Alexandrescu, 2010 ) и запущенного на персональном компьютере авторов. Моделирование нейронных сетей проводилось с помощью нейронного симулятора, написанного авторами на языке программирования D. Симулятор использует OpenCL ( Stone et al., 2010 ) для работы как на ресурсах GPGPU (AMD Radeon HD 5830 на персональном компьютере авторов), так и на ресурсах ЦП (кластер высокопроизводительных вычислений в Университете Брандейса). Исходный код всех моделей доступен на странице автора.
Подбор модели для теста вознаграждения проводился с использованием пакета SciPy ( Jones et al., 2001 ) и языка программирования Python ( van Rossum and Drake, 2001 ).
Конкретная машина Гельмгольца, реализованная в этой статье, состоит из двух наблюдаемых единиц y и двух скрытых единиц x (рисунок 1B ). Здесь «наблюдаемый» означает, что данное устройство напрямую получает сенсорные данные из окружающей среды (таким образом, наблюдая за окружающей средой), в то время как «скрытый» означает, что он делает это косвенно (т. Е. Окружающая среда скрыта от него). На практике наблюдаемые единицы могут моделировать ранние сенсорные области мозга, в то время как скрытые единицы могут моделировать более поздние сенсорные области. Каждая единица кодирует одну непрерывную неотрицательную величину. Генеративная модель и приблизительная модель распознавания параметризованы генеративными весами, генеративными смещениями, весами распознавания и смещениями распознавания.
Веса и смещения изучаются с помощью алгоритма обучения без учителя, называемого алгоритмом бодрствования-сна ( Hinton et al., 1995 ). Он состоит из двух квазисимметричных фаз: бодрствования и сна. Во время фазы пробуждения выборки y ( n ) берутся из набора обучающих данных и используются для генерации выборок x ( n ) из приближенной модели распознавания. Затем генеративные веса и смещения используются для восстановления обучающих данных, а ошибка реконструкции используется для корректировки генеративных весов. В нашей модели для этой цели используется правило дельты:
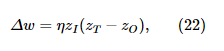
где z I - значение входной единицы (в данном случае одна из скрытых единиц), z O - значение выходной единицы (в данном случае восстановленные обучающие данные для одной из наблюдаемых единиц), а z T - это целевое значение (в данном случае истинное значение обучающих данных). w может быть либо весом между двумя единицами измерения на разных уровнях (в данном случае генерирующим весом сверху вниз), либо весом смещения, и в этом случае значение входной единицы принимается равным β. Во время фазы сна образцы x ( n )взяты из априорного распределения (эквивалентно они взяты из распределения по скрытым единицам, обусловленным активностью высших областей мозга). Затем они проходят через внутреннюю генеративную модель для генерации выборок y ( n ) . Затем веса распознавания и смещения корректируются с использованием того же правила (см. Уравнения 5–8 в разделе «Методы»).
Каждый блок вычислительной машины Гельмгольца реализован с использованием микросхемы нейронов с импульсами (рис. 2А ). Эта сеть состоит из небольших пулов (по 10–20 нейронов в каждом), создающих редкие, но специфические связи (см. Таблицу S4 для параметров связности) друг с другом. Сеть взаимодействует с другими устройствами через пул ввода (обозначен E ), пул вывода (обозначен O ) и целевой пул (обозначен T). Мы интерпретируем среднюю скорость срабатывания нейронов в этих пулах (усредненную по отдельным нейронам) как входную, выходную и целевую активность блока, реализуемого этой нейронной сетью. Входной и целевой пулы реализованы как генераторы цепочек пуассоновских спайков, в то время как остальные нейроны в сети следуют динамике, описанной в уравнении (10). В коротком временном масштабе сеть реализует условное распределение единиц (уравнения 1, 4); то есть выходная скорость r O стохастически выбирает из распределения, которое является функцией входной скорости r E и внутренне кодированных весов (кодирование обсуждается ниже). В более длительном масштабе времени сеть за счет синаптической пластичности регулирует среднее значение r O(усредненное по этой более длительной шкале времени), чтобы соответствовать r T в соответствии с правилом дельты (уравнение 22).
Эти два поведения , которые реализуются за счет использования оставшихся бассейнов в сети, помеченные I , M и D . Общая архитектура сети управляется ограничением, заключающимся в том, что r O не зависит (в максимально возможной степени) от r T в течение короткого периода времени (поскольку условное распределение, реализуемое сетью, не имеет такой краткосрочной зависимости), несмотря на то, что r T делает подключения к микросхеме для реализации правила дельты (в нашей модели нейроны общаются исключительно с помощью шипов). Это достигается за счет того, что пул T устанавливает возбуждающее соединение с пулами M иО , в то время имея бассейн М подключиться к бассейну O через промежуточную ингибирующую пул D . Этому расположению помогают приблизительно линейные кривые FI компонентных типов нейронов (рис. 2C ). Общий эффект этого соединения является то , что если сеть прочность подключения из пула E на бассейн M является возбуждающей, тем увеличение г Е приведут к уменьшению г O . Противоположное происходит, если сетевое соединение является запрещающим. Таким образом, этот баланс между возбуждением и запретом с прямой связью реализует веса вычислительного блока, которому соответствует эта сеть.
Пулы I и M несут ответственность за корректировку этого баланса в соответствии с правилом дельты. Синаптическая сила связей, создаваемых нейронами пула I с пулом M , регулируется правилом пластичности на основе шипов, которое реализует (при соответствующих условиях) определенную форму правила BCM, основанного на скорости ( Bienenstock et al., 1982 ). Это правило регулирует синаптическую силу на основе пресинаптической частоты срабатывания ( r I ) и пост-синаптической скорости срабатывания ( r M ):
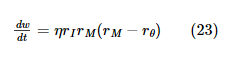
В классической формулировке правила BCM r θ будет зависеть от среднего значения r M в течение длительного периода времени, но в нашей модели оно остается постоянным. Микросхема реализует дельта-правило, применяя следующие два ограничения. Во-первых, когда r T ≥ r O , то это означает, что r M ≥ r θ . Во-вторых, когда r T < r O , то это означает, что r M < r θ. Учитывая эти идентичности соотношений скоростей, знак изменения веса, который возникает из правила синаптической пластичности BCM (уравнение 23) при определенных r I , r O и r T , соответствует знаку , возникающему из правила дельты (уравнение 22). Таким образом, сеть приближает линейную форму правила дельты (рисунок 2B , тонкая линия) к нелинейной форме правила BCM (рисунок 2B, жирная линия). Помимо сохранения знака, это довольно грубое приближение, и потребуется проверка, чтобы убедиться, что он по-прежнему правильно работает в задачах, где он предназначен для замены правила дельты. Мы хотим подчеркнуть, что это приближение будет использоваться далеко за пределами приблизительно линейной области вблизи r θ ; т.е. мы не линеаризуем правило BCM вокруг r θ . Помимо этих пластиковых соединений, остальные синаптические связи являются фиксированными, оптимизированными для реализации вышеупомянутых ограничений.
Чтобы полностью определить импульсную нейронную сеть на рисунке 2A, необходимо уточнить, что имеется в виду под скоростью (поскольку она не имеет независимого от модели определения для нейронов с импульсами) и точную природу правила синаптической пластичности на основе спайков, которое реализует основанное на частоте Правило BCM, необходимое для работы описанной выше микросхемы.
В этой статье мы сопоставим два правила на основе спайков, которые реализуют правило BCM для определенных классов пре- и постсинаптических цепочек спайков. Первая - это минимальная, но нереальная реализация, которую мы называем правилом Spiking BCM . Вторая - это упрощенная версия пластичности, зависящей от триплетов, зависящей от времени, которая, как уже известно, может реализовывать правило BCM ( Pfister and Gerstner, 2006 ). Мы называем эту сокращенную версию пластичностью ингибирования, зависящей от времени пика , или STDPi .
Правило Spiking BCM оценивает постсинаптическую скорость  путем фильтрации последовательности постсинаптических спайков с использованием экспоненциально затухающего ядра (рис. 3А , слева). Во время каждого пресинаптического всплеска синаптический вес усиливается или понижается в зависимости от мгновенного значения
путем фильтрации последовательности постсинаптических спайков с использованием экспоненциально затухающего ядра (рис. 3А , слева). Во время каждого пресинаптического всплеска синаптический вес усиливается или понижается в зависимости от мгновенного значения 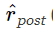 (Рисунок 3C , слева). Синаптический вес никак не регулируется во время постсинаптических всплесков.
(Рисунок 3C , слева). Синаптический вес никак не регулируется во время постсинаптических всплесков.
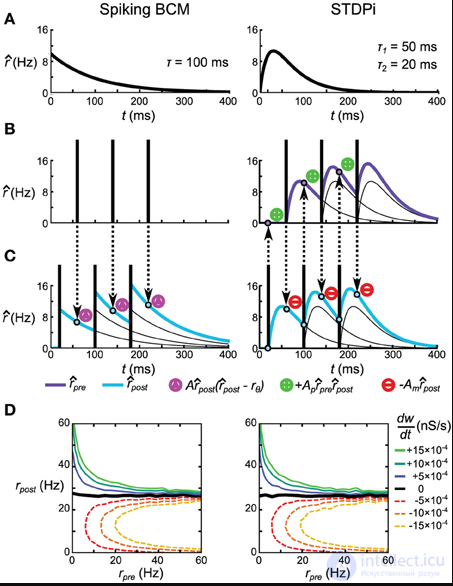
Рис. 3. Правила пластичности на основе пиков, которые реализуют правило BCM на основе скорости. (A) Ядра, используемые для оценки пресинаптической (только STDPi) и постсинаптической (оба правила) скорости. Ядро для Spiking BCM представляет собой экспоненциальный скачок и спад с единственной постоянной времени, а ядро для STDPi - это разность двух экспонент. Оба ядра равны нулю при t <0. (B, C) Схематическая диаграмма работы двух правил при заданной последовательности пресинаптических спайков (B) и последовательности постсинаптических спайков (C). Описанные пурпурные треугольники означают, что Spiking BCM регулирует синаптический вес (как в положительном, так и в отрицательном направлении). Описанные зеленые плюсы и красные минусы означают, что STDPi соответственно усиливает и понижает синаптический вес. (D) dшdтdшdт как функция некоррелированных, распределенных Пуассона пре- и постсинаптических скоростей.
Правило STDPi фильтрует как пресинаптическую серию спайков, так и постсинаптическую серию спайков с ядром разности экспонент (рис. 3A , справа), чтобы оценить как пре-, так и постсинаптическую скорость (рˆpre и 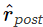 соответственно). Во время пресинаптических спайков вес снижается пропорционально мгновенному значению
соответственно). Во время пресинаптических спайков вес снижается пропорционально мгновенному значению 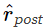 . Во время постсинаптических всплесков вес потенцируется пропорционально произведению мгновенных значений
. Во время постсинаптических всплесков вес потенцируется пропорционально произведению мгновенных значений 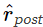 и рˆpre . Это отличается от правила Spiking BCM, где потенцирование и депрессия происходят только во время пресинаптических всплесков. В этом смысле STDPi более точно напоминает экспериментальные кривые пластичности ( Haas et al., 2006 ). Это правило аналогично упрощенному правилу триплетного STDP, исследованному Пфистером и Герстнером (2006), с той разницей, что форма ядра (в их работе использовалось экспоненциальное ядро, как в правиле Spiking BCM) и тем фактом, что только одна трасса используется для оценки постсинаптической скорости (в отличие от двух в их работе).
и рˆpre . Это отличается от правила Spiking BCM, где потенцирование и депрессия происходят только во время пресинаптических всплесков. В этом смысле STDPi более точно напоминает экспериментальные кривые пластичности ( Haas et al., 2006 ). Это правило аналогично упрощенному правилу триплетного STDP, исследованному Пфистером и Герстнером (2006), с той разницей, что форма ядра (в их работе использовалось экспоненциальное ядро, как в правиле Spiking BCM) и тем фактом, что только одна трасса используется для оценки постсинаптической скорости (в отличие от двух в их работе).
Если мы возьмем две некоррелированные, распределенные Пуассоном последовательности пре- и постсинаптических спайков и пропустим их по этим двум правилам, мы увидим, что они дают одинаковые значения для 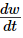 как функция скорости этих шиповых поездов (рис. 3D ). Эта эквивалентность зависит только от значений A , A m и A p и τ, но не от постоянных времени ядер STDPi. Кроме того, можно видеть, что пресинаптическая скорость влияет только на величину
как функция скорости этих шиповых поездов (рис. 3D ). Эта эквивалентность зависит только от значений A , A m и A p и τ, но не от постоянных времени ядер STDPi. Кроме того, можно видеть, что пресинаптическая скорость влияет только на величину  т а не его знак, как в правиле BCM (уравнение 23). Фактически, для поездов с распределенными выбросами Пуассона оба правила точно реализуют уравнение 23. См. Дополнительную информацию для полного вывода этих фактов.
т а не его знак, как в правиле BCM (уравнение 23). Фактически, для поездов с распределенными выбросами Пуассона оба правила точно реализуют уравнение 23. См. Дополнительную информацию для полного вывода этих фактов.
Чтобы реализовать машину Гельмгольца (рис. 1B ), мы организуем четыре сети дельта-правил, или единицы, как мы теперь будем их называть (рис. 4 , для ясности показаны только три модуля), на два уровня и устанавливаем связи между модулями разных уровней. Две из этих единиц соответствуют переменной y (сенсорный слой), а две другие - переменной x (скрытый слой). Поскольку сеть правил дельты работает с частотой срабатывания пулов нейронов, реализация нейронной сети Машины Гельмгольца кодирует значения этих переменных с помощью кодирования скорости. В этой сети средние скорости (в течение окна 500 мс) пулов X 0 , X 1 , Y0 и Y 1 (в совокупности, выходные пулы) представляют реализации случайных величин x 0 , x 1 , y 0 и y 1 соответственно. Распределение вероятностей по этим переменным моделируется посредством стохастической изменчивости этих скоростей, возникающей как из-за вариаций скорости неспецифических внешних входов в пулы сети M и O правил дельты (см. Подпись к рисунку 2).и методы), а также стохастическое высвобождение синаптических пузырьков в синапсах сети. По построению, выходные пулы выбираются (см. Рисунок S1) из распределения вероятностей, обусловленного скоростью входных пулов (т. Е. Выходных пулов других единиц), взвешенных по синаптической силе соединений, которые они устанавливают в пул M каждого единица. Кроме того, существуют пулы, которые создают пластиковые соединения с пулами ввода, которые активны неспецифически. Эти связи моделируют предубеждения в вычислительной модели. См. Таблицу S4 для получения информации о параметрах подключения. Вычислительные веса и смещения (а именно W G , W R , B G и B R) соответствуют общему влиянию выходных сигналов модулей на скорость вывода устройств, к которым они подключаются. С точки зрения реализации нейронной сети это соответствует балансу между подавлением прямой связи и возбуждением.
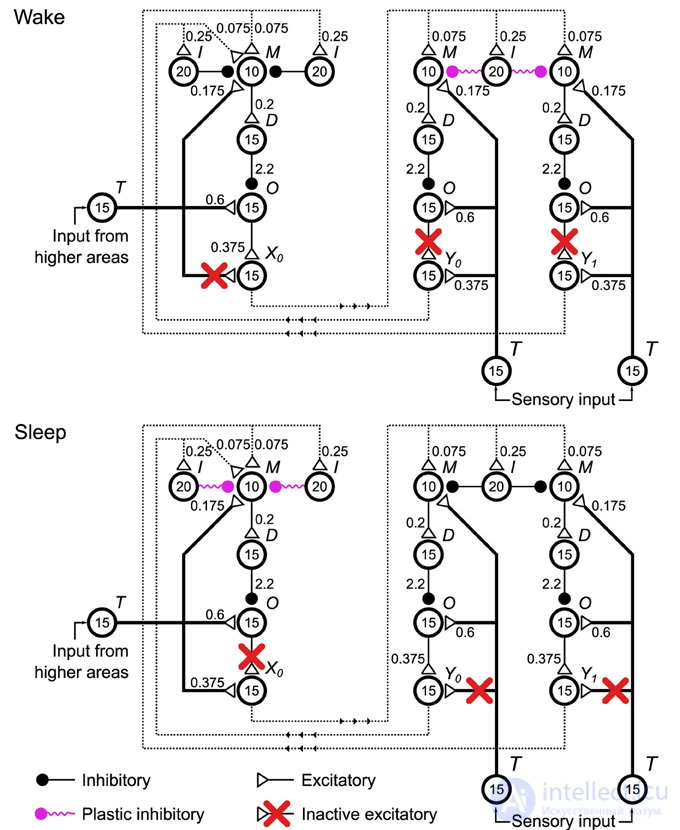
Рис. 4. Конфигурации реализации нейронной сети с пиками машины Гельмгольца во время фаз бодрствования и сна при обучении . Четыре сети дельта-правил (рис. 2A ), называемые в контексте этой сети блоками, соединены вместе, чтобы сформировать машину Гельмгольца, две из которых обрабатывают вычисления сенсорного уровня, а две - вычисления скрытого слоя (только одна показана на рисунке). этот рисунок для наглядности). См. Подпись к рисунку 2 для объяснения используемых символов. Для поддержки двух фаз алгоритма бодрствования-сна некоторые соединения (красные кресты) деактивируются для управления тем, что определяет скорость срабатывания выходных пулов каждого устройства (пулы X 0 , X 1 , Y0на этом рисунке). В фазе бодрствования (вверху) выходы сенсорных единиц определяются сенсорным входом, в то время как выходы скрытых единиц определяются скоростью активации и соответствующей силой соединения выходов сенсорных единиц. В фазе сна выходы сенсорных блоков определяются скоростью активации и соответствующей силой соединения выходов скрытых блоков, в то время как выходы скрытых блоков управляются входом из более высоких областей. Кроме того, в соответствии с алгоритмом бодрствования-сна, прочность пластиковой связи с сенсорными единицами изменяется только во время фазы бодрствования, и наоборот, сила связи со скрытыми единицами. Неспецифические внешние входы внутри каждого блока не показаны. Также не показаны пластиковые входы в бассейн.M каждой единицы, реализующей смещение и веса. Они моделируются как последовательность импульсов Пуассона с частотой r b = 25 Гц. Эти пластиковые входы образуют такой же пластиковый тормозной синапс, что и все другие пластиковые соединения, показанные на рисунке.
Конкретные внешние соединения выполняются через пул T каждого устройства (в совокупности внешние пулы ввода). Они моделируются как шиповые поезда со статистикой Пуассона. В этом случае скорость этих процессов остается постоянной для каждого интервала 500 мс, а затем выбирается новая скорость из рассматриваемого распределения вероятностей (внешний мир или априорные значения).
Нейронная сеть использует адаптированный алгоритм бодрствования-сна (рисунок 5 Обучение). Для поддержки двух этапов алгоритма обучения в этой сети мы ввели два набора переключаемых соединений. Первый набор включает соединения в каждом модуле, которые идут от пула T к пулу вывода. Второй набор включает соединения в каждом модуле, которые идут от пула O к пулу вывода. Эти соединения контролируют то, что определяет реализации случайных величин: скорости r X 0 , r X 1 , r Y 0 , r Y 1 в этой
продолжение следует...
Часть 1 Машина Гельмгольца и генеративная модель
Часть 2 3. Результаты - Машина Гельмгольца и генеративная модель
Часть 3 3.2. Результаты сети правил дельты - Машина Гельмгольца и генеративная
Часть 4 4. Дискуссия - Машина Гельмгольца и генеративная модель
Данная статья про машина гельмгольца подтверждают значимость применения современных методик для изучения данных проблем. Надеюсь, что теперь ты понял что такое машина гельмгольца, алгоритм бодрствования-сна и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Вычислительный интеллект
Комментарии
Оставить комментарий
Вычислительный интеллект
Термины: Вычислительный интеллект