Лекция
Это продолжение увлекательной статьи про машина гельмгольца.
...
сети. В вычислительной модели реализацияy 0 , например, может быть взят из среды или из внутренней генеративной модели. В сенсорных устройствах в нейронной сети, например, это определяется ли активное соединение с выходным бассейном сделано из внешнего входного пула, или из бассейна O . В том же духе эти связи можно рассматривать как определение того, генерирует ли блок выборка из своего условного распределения вероятностей. Например, во время фазы пробуждения для корректировки генеративных весов мы вычисляем W G x ( n ) + B G b(Уравнение 6), но мы не используем это восстановленное среднее значение для создания выборки из внутренней генеративной модели. В нейронной сети, например, во время фазы пробуждения соединение между пулом O сенсорной единицы и выходным пулом разрывается, чтобы предотвратить отправку этой выборки скрытым единицам. См. В разделе «Обсуждение» мысли о природе этих процессов переключения в головном мозге.
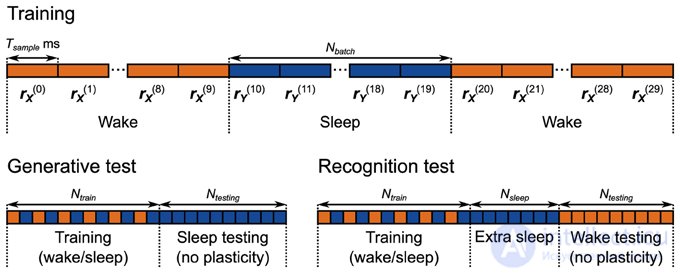
Рисунок 5. Протоколы обучения и тестирования для реализации нейронной сети Машины Гельмгольца . Сеть обучается в течение 5000 с с использованием чередования фаз бодрствования и сна. Каждая фаза бодрствования и сна состоит из 10 выборок по 500 мс каждая. Во время генеративного теста из генеративной модели собрано 2000 образцов.
Кроме того, силы связи с сенсорными единицами (соответствующие генерирующим весам W G и смещениям B G ) изменяются только во время фазы бодрствования, а веса связи со скрытыми единицами (соответствующие генерирующим весам W R и смещениям B R ) изменяются только во время фазы сна. Сенсорный вход и вход из более высоких областей во время фаз сна и бодрствования соответственно установлены на устойчивые 40 Гц.
В отличие от вычислительной модели, каждая фаза бодрствования и сна состоит из нескольких последовательных выборок на фазу. Это сделано для того, чтобы минимизировать влияние переходных процессов скорости, которые происходят, когда сеть переключается между фазами сна и пробуждения. Например, когда сеть переключается с фазы пробуждения на фазу сна, скорость пула M в скрытых модулях (рисунок 4 ) переключается с работы с образцами, взятыми из окружающей среды, на работу с образцами, созданными генеративной моделью. Несмотря на то, пластичность выключена в этих единицах во время фазы бодрствования, ядро , которые оценивают скорость нейронов в этих бассейнах (рис 3) по-прежнему функционируют. Это означает, что первоначально во время первой выборки фазы сна, следующей за фазой бодрствования, расчетная частота неверна, что вызывает ошибки в обучении. Аналогичная проблема затрагивает соседние выборки в фазе бодрствования и соседние выборки в фазе сна, но поскольку скорости берутся из одних и тех же распределений (из окружающей среды и из предыдущего соответственно), это менее серьезная проблема. Эти проблемы ограничивают временную шкалу динамики нейронов, правила пластичности и механизмы активных ощущений (например, саккады). Если окружающая среда изменяется быстрее во время фазы бодрствования (или более высокие области мозга колеблются в активности во время фазы сна) быстрее, чем может успевать механизм оценки скорости, на обучение будет оказано неблагоприятное воздействие.
Эта проблема означает, что выбор количества образцов на фазу может иметь решающее значение для успешного обучения. На практике мы обнаруживаем, что этот выбор зависит от сложности данных и предшествующих распределений. Сложные задачи (бимодальные наборы данных и априорные задачи) требуют больших размеров пакета. Мы используем размер пакета 10 для большинства задач, увеличивая его до 50 для более сложных тестов распознавания. Наши тесты показывают, что как только размер партии превышает определенное количество, производительность сети выходит на плато для небольшого (≤ 50) количества образцов на фазу.
Чтобы проверить функциональность нейронной сети правила дельты, мы взяли 121 отдельную, но структурно идентичную сеть для каждого правила пластичности. Каждая сеть получила различную целевую скорость r T и различный начальный средний вес пластмассовых соединений w start . Все остальные параметры оставались такими же, с r E , установленным на уровне 20 Гц. Затем мы моделировали каждую сеть в этих условиях и записали г O . Перед тренировкой r O увеличивалось с увеличением w start (Рисунок 6A , слева). Изменение r O как функция r Tдо обучения идет несовершенная линейность сети. После 50 секунд обучения r O теперь следует за r T, когда сеть использовала правило BCM Spiking и когда она использовала STDPi (рис. 6A , посередине, справа). Обратите внимание, что если мы изменим r T в коротком временном масштабе, r O останется неизменным (по модулю недостатков, упомянутых выше): характер изменения r O происходит из-за того, что r I влияет на него по-разному в зависимости от тренированных весов. Чтобы более четко изучить, насколько хорошо r O соответствует обучению r Tмы моделируем 50 экземпляров случайного подключения для каждой из 121 сети, указанной выше, и усредняем начальные веса. Для правила BCM пиковых значений мы отмечаем, что отклонение между r T и r O примерно постоянное для всех r T (рисунок 6B , красная линия), в то время как для STDPi это отклонение увеличивается с увеличением r T (рисунок 6B , синяя пунктирная линия). Если мы посмотрим на изменения веса при w start = 1 (рисунок 6C), можно видеть, что это связано с тем, что STDPi не увеличивает синаптический вес так сильно, как Spiking BCM в этих условиях. Это не проблема сходимости, поскольку, глядя на общее изменение веса во времени для одного испытания, усредненное по 50 сетям, становится ясно, что оба веса сходятся для обоих правил во время обучения (рис. 6D ). Несмотря на эти недостатки, по крайней мере, в этой простой задаче, использование правила приблизительной дельты и его реализация с использованием правил пластичности пиков не приводит к катастрофическому ухудшению производительности, и мы можем перейти к попыткам использовать эту сеть как часть Машина Гельмгольца.
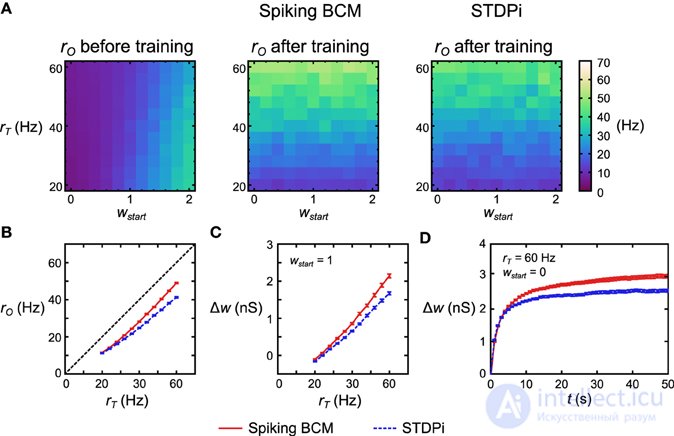
Рисунок 6. Производительность нейронной сети с правилом дельты. (A) Для каждого правила пластичности 121 структурно идентичной сети были заданы различные r T и начальные веса w start . Затем сети моделировались в течение 50 с. Перед тренировкой г вывод следует ш начала и в значительной степени зависит от р Т . После обучения r O следует за r T (точнее, следует за w, которое было обучено r T, поскольку r O в значительной степени не зависит от r Tв краткосрочных масштабах). (B) Усреднение по 50 экземплярам вышеупомянутой 121 сети дельта-правил и сжатие вдоль начальной оси w , отклонение от r T почти постоянно для всех значений r T, когда используется пиковое значение BCM (красный сплошной цвет), но это не так. -постоянно при использовании STDPi (синяя пунктирная линия). (C) Сети, в которых используется протокол STDPi, не могут достичь высоких значений веса. (D) Изменение веса с течением времени для одного испытания 50 сетей. Для обоих правил пластичности веса приближаются к определенному устойчивому состоянию, но для STDPi это окончательное значение веса ниже, чем для Spiking BCM. Планки погрешностей - SEM.
Сначала мы тестируем вычислительную модель и нейронную сеть в генеративном режиме. То есть мы проверяем, насколько хорошо модель соответствует распределению вероятностей по входным единицам, на которых она была обучена. Это наиболее применимо для сопоставления спонтанной нейронной активности in vivo в ранних областях коры (напр., Ранняя сенсорная кора Berkes et al., 2011 ). Вычислительная модель и нейронная сеть обучаются на девяти наборах данных (помечены от a до i ). Наборы данных от a до e состоят из унимодальных двумерных усеченных гауссианов с перекосом и без перекоса, а наборы данных от f до iпредставляют собой бимодальные смеси неискаженных двумерных гауссиан. Для одномодальных наборов данных мы используем одномодальное априорное распределение (уравнение 15), тогда как для бимодальных наборов данных мы используем бимодальное априорное распределение (уравнение 16). В нейронных сетях различные априорные распределения реализуются путем изменения распределения частоты срабатывания пула T в скрытых блоках во время фазы сна. Такой выбор априорных значений вручную, зависящий от задачи, необходим, потому что наша модель содержит только один скрытый слой; сила Машины Гельмгольца заключается в ее способности быть реализованной в иерархической структуре, так что тип предшествующего может быть изучен как сила связи для второго скрытого уровня в более крупной модели.
Модели обучаются и тестируются в соответствии с протоколом, изображенным на рисунке 5., Генеративный тест. Каждый сеанс начинается с периода обучения общей продолжительностью 5000 с (всего 500 фаз бодрствования и 500 фаз сна, где каждая фаза включает 10 выборок) для нейронной сети. Вычислительная модель обучена для 250 000 фаз бодрствования и сна (по одному образцу на фазу). Мы используем относительно более высокую скорость обучения нейронной сети ради вычислительной эффективности. В то же время, однако, он на 90% медленнее, чем был в сети правил дельты, потому что веса не сходятся правильно, если скорость обучения слишком высока. Это не было проблемой в сети правил дельты из-за постоянных входных данных, которые она получала во время обучения. Порядок представления данных был случайным для каждого сеанса (см. Материалы и методы). Каждое занятие, после тренировки, мы исследуем генеративную модель как нейронной сети, так и вычислительную модель, собирая из нее 2000 выборок. Мы исследуем 50 отдельных сетей, каждая из которых имеет разные экземпляры случайного подключения, чтобы изучить влияние проблем с подключением, описанных выше. Мы записываем один такой сеанс в каждой сети.
Сначала мы исследуем, как нейронные сети работают при обучении на унимодальных наборах данных (рисунок 7A , первый столбец) с унимодальным априорном (рисунок 7B ). Чтобы иметь возможность сравнения, мы также исследуем гистограммы генеративных моделей, полученных из вычислительной модели, обученной на тех же наборах данных и с одними и теми же предварительными данными (рис. 7A , второй столбец). Несмотря на использование приблизительного правила обучения (уравнение 9) вычислительной модели удается точно изучить генеративные модели. Мы количественно оцениваем это, вычисляя сходство между генеративными моделями и всеми наборами обучающих данных. Мы измеряем сходство с помощью расхождения Дженсена-Шеннона ( Lin, 1991).), который варьируется от 0 для абсолютно идентичных распределений вероятностей до 1 для распределений без перекрытия. Мы смотрим на D net, которое представляет собой среднее расхождение между наборами данных, и D pop, которое является средним D net для всех случайных экземпляров модели.
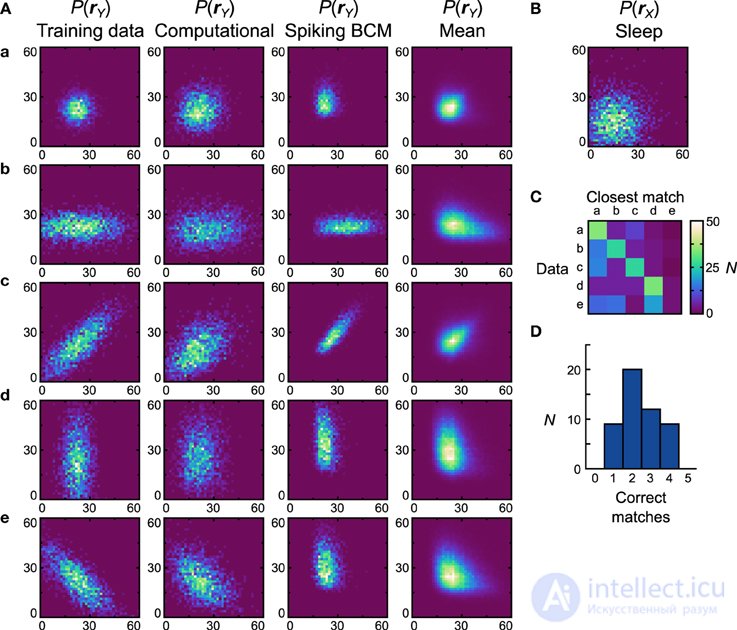
Рисунок 7. Производительность реализации нейронной сети машины Гельмгольца с правилом Spiking BCM и унимодальными наборами данных. (A) Вычислительная модель и 50 экземпляров нейронных сетей были обучены на пяти унимодальных наборах данных, показанных в первом столбце. Оси в диапазоне от 0 до 60 Гц на обоих компонентах г Y . Результирующие генеративные модели из вычислительной модели показаны во втором столбце. Генеративные модели самой эффективной (с точки зрения соответствия распределений обучающих данных с изученными генеративными моделями) нейронной сети показаны в третьем столбце. Четвертый столбец отображает средние популяции генеративных моделей нейронных сетей. (В)Априорное распределение, используемое для генеративных моделей. Оси в диапазоне от 0 до 60 Гц на обоих компонентах г X . (C) Матрица путаницы, полученная путем сопоставления генеративных моделей отдельных сетей со средними (вычисленными по всем сетям для данного набора данных) генеративными распределениями. (D) Гистограмма количества правильных совпадений каждой нейронной сетью.
После вычисления матрицы сходства мы смотрим на набор данных, который наиболее похож на генеративную модель, и, если он соответствует набору данных, который использовался для обучения, мы заявляем, что модель правильно изучила набор данных. По этой метрике вычислительная модель изучила все представленные наборы данных ( D net = D pop = 0,19). Для реализации нейронной сети мы исследуем два правила пластичности отдельно. Мы генерируем 50 отдельных сетей, каждая с разными экземплярами случайного подключения, и исследуем производительность в этих реализациях сети. Начиная с сетей, в которых использовалось правило Spiking BCM, генеративные модели лучшей сети (т. Е. Той, которая дала наибольшее количество совпадений) показаны на рисунке 7A., третий столбец ( D net = 0,35). Во всех экземплярах нейронная реализация не смогла сопоставить набор данных e ( D pop = 0,39 ± 0,012 SEM).
Набор данных e представляет проблему для нейронной сети, поскольку он требует компонентов yбыть антикоррелированным, что в этой модели может быть достигнуто только с отрицательными генеративными весами. Сеть правил дельты способна представлять отрицательные веса, регулируя баланс между возбуждающими и тормозящими входными соединениями с прямой связью. Однако диапазон весов, который он может представлять, не симметричен относительно нуля, что делает невозможным получение очень отрицательных весов, необходимых для моделирования некоторых распределений. Причина такой асимметрии кроется в том, что в нашей сети пластичны только тормозные связи. Сильный отрицательный вес требует сильного возбуждения с прямой связью, которому трудно противодействовать пластическим ингибированием, когда требуются неотрицательные веса. Поэтому используется относительно слабое возбуждение с прямой связью, что приводит к ограниченной способности представлять отрицательные веса. Эта проблема может быть решена путем использования более сложного метода кодирования совокупности (см. Обсуждение). Таким образом, мы не предполагаем, что это будет актуальной проблемой для мозга.
Поскольку сети производили генеративные модели, совершенно отличные от наборов данных, на которых они были обучены, более информативно вычислять матрицу сходства относительно распределений вероятностей, полученных путем усреднения генеративных моделей всех сетей, обученных на конкретном наборе данных (рис. 7A). , четвертый столбец). Этот анализ покажет, отличаются ли генеративные модели, изученные сетями, для разных наборов данных. Если сети отлично справляются с этой задачей, то набор данных среднего распределения, на которое наиболее похожа генеративная модель сети, будет соответствовать набору данных, на котором была обучена сеть. Мы можем изобразить это, используя матрицу неточностей (рис. 7C).) для всех нейронных сетей. Мы видим, что для первых четырех наборов данных большинство сетей создают генеративные модели, которые хорошо соответствуют среднему распределению, но терпят неудачу при попытке сопоставить среднее распределение набора данных e . Гистограмма производительности, показывающая количество правильных совпадений в каждой сети (рис. 7D ), показывает, что ни одна сеть не соответствует всем пяти наборам данных, а большинство сетей соответствуют только двум.
Затем мы исследуем, как нейронные машины Гельмгольца с правилом пластичности STDPi работают с одними и теми же унимодальными наборами данных. Когда это правило использовалось в сетях с изолированными дельта-правилами, уже можно было наблюдать отклонения производительности от правила Spiking BCM, поэтому мы также ожидали различной производительности в этой задаче. Одним из результатов исследования сети правил дельты было то, что когда она использовала правило STDPi, она не могла соответствовать высоким целевым показателям (рис. 6B).). Чтобы компенсировать это, мы умножили на три все предыдущие скорости, использованные как в вычислительной модели, так и в сети с помощью правила пластичности BCM (наборы обучающих данных остались прежними). Прискорбным побочным эффектом этого является то, что подробное поведение сети, полученное с помощью этого правила, можно только качественно сравнить с тем, которое создается правилом Spiking BCM.
На рисунке 8A показаны наборы данных (первый столбец), генеративные модели лучшей сети (второй столбец) и средние распределения (третий столбец). Предыдущее использованное устройство показано на рисунке 8B . D net лучшей сети составляет 0,47 и D pop= 0,53 ± 0,13 SEM. Понятно, что сети, использующие STDPi, имеют проблемы с сопоставлением данных даже качественно (лучшая сеть правильно соответствует только первым трем наборам данных). Сети имеют тенденцию создавать положительно коррелированные распределения вероятностей независимо от обучающих данных, хотя уровень корреляции модулируется в правильном направлении. Как и прежде, мы также исследуем, насколько различаются генеративные модели, которые обучаются на разных наборах данных, путем вычисления матрицы неточностей (рис. 8C ) и соответствующей гистограммы соответствия (рис. 8D).). Несмотря на относительно низкую производительность при сопоставлении распределений данных, сети действительно изучают распределения, которые различаются при обучении на разных наборах данных. Пять (10%) сетей соответствовали всем пяти наборам данных, хотя, как и в случае с правилом Spiking BCM, большинство соответствовали только двум.
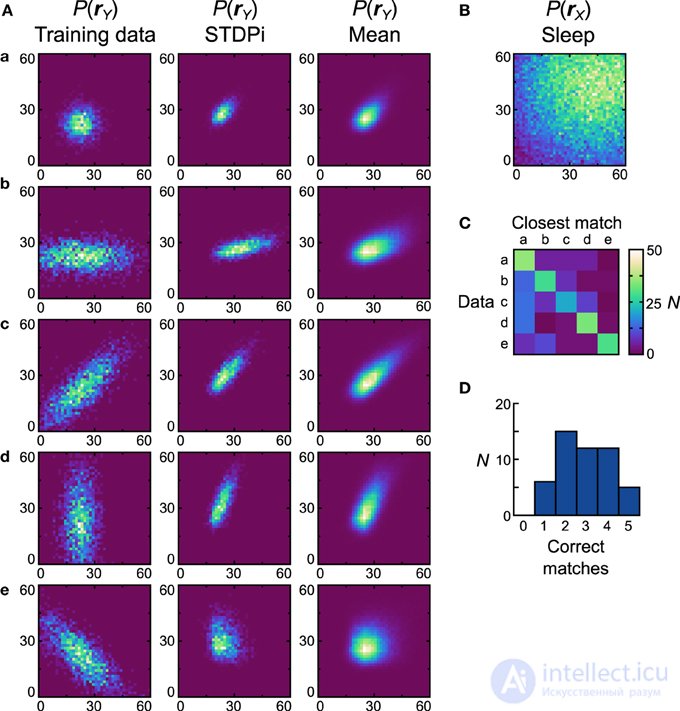
Рисунок 8. Производительность реализации нейронной сети Машины Гельмгольца с правилом STDPi и одномодальными наборами данных . См. Рисунок 7 для объяснения панелей. Параметры для ядер STDPi: τ 1 = 50 мс, τ 2 = 20 мс.
Рисунки 7 , 8 выполнены с бимодальными наборами данных (Рисунок 9A , первый столбец) и предыдущими (Рисунок 9B ). Опять же, вычислительная модель не имеет проблем с этими наборами данных (рис. 9A , второй столбец), что приводит к близкому качественному и количественному совпадению (производительность идеального совпадения при использовании теста совпадения, D net = D pop = 0,30). Начиная с правила пластичности Spiking BCM, генеративные модели из наиболее эффективной нейронной сети (рис. 9A , третий столбец) качественно напоминают наборы данных, на которых они были обучены, и, хотя производительность сопоставления идеальна, D netявляется относительно плохим 0,62 ( D pop = 0,58 ± 0,0075 SEM). Изучая средние распределения, становится ясно, что большинство сетей плохо работают с набором данных g . Причины этого схожи с причинами, по которым нейронные сети плохо работают с набором данных e , а именно с необходимостью сильных отрицательных связей. Выполнение теста на соответствие средних распределений дает матрицу неточностей (рисунок 9C ) и гистограмму производительности (рисунок 9D ). Семь (14%) сетей соответствуют всем четырем средним распределениям.
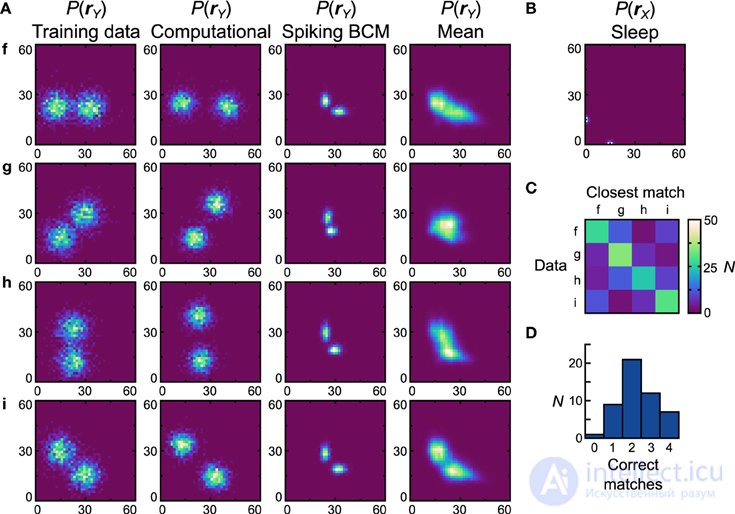
Рисунок 9. Производительность реализации нейронной сети машины Гельмгольца с правилом Spiking BCM и бимодальными наборами данных . См. Рисунок 7 для объяснения панелей.
Сети, использующие правило STDPi, лучше работают с бимодальными наборами данных (рис. 10A , первый столбец) и бимодальными априорными данными (рис. 10B ). Генеративные модели лучшей сети выглядят качественно похожими на наборы данных (рис. 10A , второй столбец), хотя D net имеет высокое значение 0,53 ( D pop = 0,59 ± 0,0082 SEM). Единственным исключением является набор данных g , который трудно изучить, поскольку он основан на хорошем представлении отрицательных весов. Глядя на матрицу неточности (рис. 10C ) и гистограмму соответствия (рис. 10D)) мы видим, насколько сильно различаются изученные распределения, полученные в результате обучения на разных наборах данных. Двадцать две (44%) сетей правильно соответствуют всем средним распределениям (рис. 10А , третий столбец).
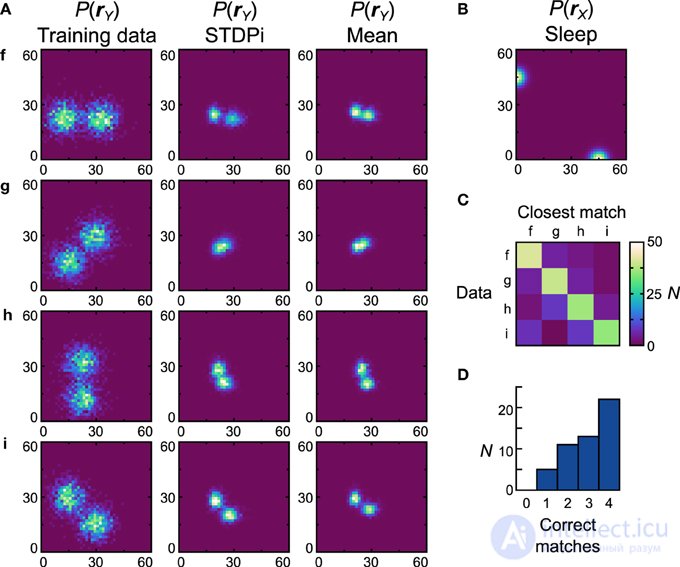
Рисунок 10. Производительность реализации нейронной сети Машины Гельмгольца с правилом STDPi и бимодальными наборами данных . См. Рисунок 7 для объяснения панелей. Параметры для ядер STDPi: τ 1 = 50 мс, τ 2 = 20 мс.
В целом, похоже, что переход от вычислительной модели к нейронной реализации влияет на производительность нетривиальным образом. Несмотря на реализацию нейронной сети и вычислительную модель, использующую приближенное правило обучения, нейронные сети работают количественно хуже по всем показанным здесь показателям. Это снижение производительности является комбинацией недостатков, уже показанных в результатах сети дельта-правил (рис. 6 ), в сочетании с ранее упомянутыми эффектами перекрестных помех между этапами обучения и несовершенством коммутируемой связи. Кроме того, фундаментальные проблемы представления весов влияют на одни классы распределений данных, но не на другие.
Правила пластичности STDPi и BCM идентичны для определенных классов пре- и постсинаптических цепочек спайков, и при использовании в более сложной и реалистичной среде сети правил дельты они также показывают относительно небольшие количественные различия. Однако в более сложной настройке нейронной машины Гельмгольца эти незначительные количественные различия усиливаются до качественных эффектов. Правило STDPi относительно плохо работает, когда сети, которые его используют, должны изучать распределение вероятностей, и даже обеспечение более благоприятного предварительного распределения не решает всех проблем.
Объяснение несоответствия очевидного сходства между правилами Spiking BCM и STDPi, показанного на рисунке 3C, и их несходства в производительности в сети дельта-правил и машине Гельмгольца заключается в краткосрочной корреляции между пре- и постсинаптическими цепочками всплесков, возникающими из-за в тормозные синапсы (соответствующие возбуждающие синапсы в этой модели относительно слабы). Можно сделать ядра, используемые для оценки скоростей, менее чувствительными к этим корреляциям, уменьшив вклад тех частей ядра, на которые эти корреляции больше всего влияют. В частности, мы корректируем форму ядра так, чтобы интервал сразу после пресинаптического всплеска вносил меньший вклад в оценку скорости. Мы делаем это, изменяя τ 2, который определяет ширину начального провала ядра STDPi (рисунок 3A ). Чтобы показать общий эффект, который этот параметр оказывает на поведение правила, мы исследуем два крайних значения τ 2 , 1 мс и 30 мс. Ядра для этих значений τ 2 показаны на рисунке 11A . Для симметрии мы используем одно и то же ядро для оценки как пре-, так и постсинаптических скоростей, хотя постсинаптическая форма ядра в значительной степени не имеет значения для этого анализа. Во-первых, мы проверяем, что STDPi, использующий оба ядра, дает такое же поведение, как показано исходным ядром STDPi (с τ 2 = 20 мс), как показано на рисунке 3B, когда последовательности всплесков не коррелированы. Рисунок 11Bпоказывает, что при изменении пре- и постсинаптической скорости мы получаем одинаковое поведение для двух форм ядра. Затем мы генерируем серию пиковых значений с краткосрочными отрицательными корреляциями. Спайки генерируются из выражений скорости с использованием процесса Пуассона (однородного в пресинаптическом случае и неоднородного в постсинаптическом случае, см. Материалы и методы). Когда мы применяем STDPi с использованием двух разных ядер на таких коррелированных цепочках спайков, мы обнаруживаем, как и ожидалось, что корреляции действительно изменяют чистую синаптическую пластичность как функцию средних пре- и постсинаптических скоростей. В частности, самым большим изменением является увеличение постсинаптической скорости, при которой синаптический вес остается неизменным во времени (рис. 11C)., черная линия - некоррелированная, фиолетовая пунктирная линия - коррелированная). Это происходит из-за того, что пресинаптическая скорость недооценивается, что приводит к меньшему усилению синаптических весов. Важно отметить, что мы видим преимущество большего τ 2 (рис. 11C , правая панель), которое улучшает не только чистую недооценку пресинаптической скорости - и, следовательно, средний сдвиг постсинаптической скорости, при котором синапсы больше не меняют силу. - но также и зависимость положения нулевого клина от пресинаптической скорости. Последнее важно, так как для воспроизведения идеального правила дельты постсинаптическая скорость в установившемся состоянии должна быть единственным фактором, влияющим на направление изменения этого синапса.
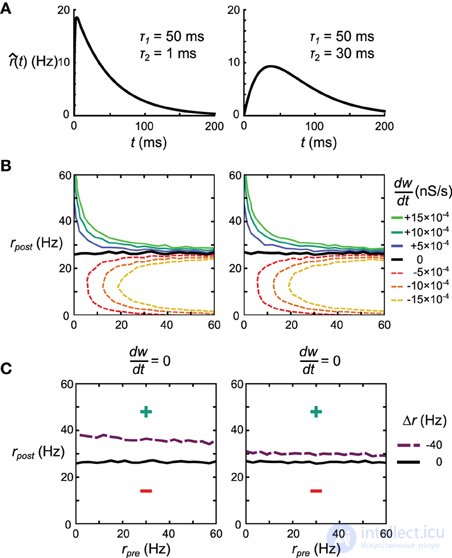
Рис. 11. Влияние формы ядра на поведение правила пластичности STDPi. (A) Две формы ядра, которые рассматриваются на этом рисунке. Одно и то же ядро используется как для пре-, так и для постсинаптической оценки скорости. (В) dшdтdшdткак функция некоррелированных, распределенных Пуассона пре- и постсинаптических скоростей для ядра с τ 2 = 1 мс (слева) и τ 2 = 30 мс (справа). (С)dшdтdшdт= 0 нульклин для некоррелированных последовательностей пре- и постсинаптических спайков, распределенных по Пуассону (черный), и отрицательно коррелированных, распределенных по Пуассону пресинаптических и неоднородно-пуассоновских постсинаптических последовательностей спайков (фиолетовый). Используемые ядра имеют τ 2 = 1 мс (слева) и τ 2 = 30 мс (справа). Все остальные контурные линии опущены для ясности.
Как описано ранее, результаты, полученные на этих искусственных примерах, не обязательно предсказывают производительность в реальных сетях. Поэтому мы проверяем, как и сеть правил дельты, и нейронная реализация машины Гельмгольца зависят от выбора τ 2 .
Для сети правил дельты мы количественно оцениваем производительность, глядя на среднее отклонение выходной скорости после обучения от целевой скорости. Мы варьируем τ 2 и смотрим на среднее отклонение по 50 сетям (дифференцированное по экземплярам случайной связности). Мы видим, что отклонение уменьшается с увеличением τ 2 (рис. 12А ). Когда τ 2 = 30 мс, среднее отклонение по разным сетям составляет 12,50 ± 0,26 (SEM) Гц, что немного меньше среднего отклонения в 10,98 ± 0,25 (SEM) Гц, полученного при использовании правила Spiking BCM.
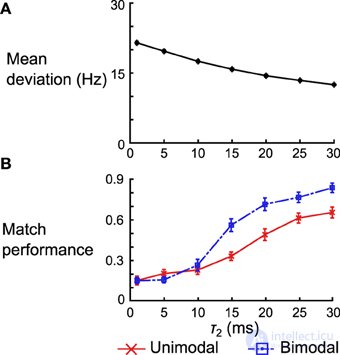
Рисунок 12. Влияние формы ядра на производительность сети дельта-правил и нейронную реализацию машины Гельмгольца. (A) Среднее отклонение (по 50 экземплярам сети) между скоростью вывода после обучения и целевой скоростью по 50 экземплярам сети правил дельты. Планки погрешностей - это SEM, но они слишком малы, чтобы их можно было увидеть на этом графике. (B) Средняя эффективность сопоставления для одномодальных и бимодальных наборов данных по 50 экземплярам нейронных реализаций Машины Гельмгольца. Планки погрешностей - SEM. Обратите внимание, что производительность нормализована по количеству наборов данных (например, производительность 1.0 означает, что все 5 средних распределений были сопоставлены в категории одномодальных наборов данных).
Для нейронной реализации машины Гельмгольца мы сосредоточимся на тесте на соответствие, выполненном на панели D на рисунках 8 , 10 . Мы смотрим как на одномодальные, так и на бимодальные наборы данных и нормализуем производительность сети по количеству наборов данных в этой группе (то есть вместо того, чтобы варьироваться от 0 до 5 для одномодальных наборов данных, теперь он колеблется от 0 до 1). Мы исследуем производительность 50 экземпляров нейронных сетей машины Гельмгольца, изменяя τ 2, как и раньше. В то время как производительность согласования увеличивается для обоих наборов данных, когда τ 2увеличивается, он увеличивается гораздо более резко для бимодальных наборов данных (переход от сопоставления в среднем 1,26 наборов данных до 3,40 наборов данных). Частично это связано с тем, что сети, использующие плохие ядра, обычно не запоминают веса, которые создают бимодальные генеративные модели. Как только ядра становятся достаточно хорошими (τ 2 > 10 мс) для разделения двух режимов, производительность резко возрастает.
Пока мы только тестировали нашу реализацию Машины Гельмгольца в генеративном режиме. Однако во время поведения и восприятия животные, скорее всего, будут использовать модель распознавания для выполнения логических выводов. Таким образом, теперь мы исследуем, насколько хорошо нейронные сети работают в режиме распознавания. Этот режим наиболее применим для сопоставления нейронных данных в высших отделах коры головного мозга, а также поведенческих данных. В этом разделе мы сосредоточены на поведенческих задачах, поскольку поведенческие данные более доступны.
Первый тест, который мы выполняем, - это простой тест линейного декодирования. Модели обучаются с использованием унифицированного линейного набора данных (рисунок 13A , набор данных o ) и предшествующего (рисунок 13B).). Во время тестирования модели должны определить, где точка представленных данных находится на линии (положение в данном случае является одномерным качеством в диапазоне от -1 до 1). Это достигается путем просмотра того, где активность скрытых юнитов находится на предшествующем (что также является линией). Критическим моментом здесь является то, что стратегия декодирования, используемая для оценки модели, явно указывается в предыдущем распределении, что означает, что преобразование от распределения данных к распределению декодированных позиций полностью изучается моделью (подробности см. В разделе «Материалы и методы»). процедуры декодирования). Модели обучаются и тестируются в соответствии с протоколом, изображенным на рисунке 5., Тест на признание. Во время каждого сеанса вычислительная модель обучается для 50 000 фаз (25 000 фаз
продолжение следует...
Часть 1 Машина Гельмгольца и генеративная модель
Часть 2 3. Результаты - Машина Гельмгольца и генеративная модель
Часть 3 3.2. Результаты сети правил дельты - Машина Гельмгольца и генеративная
Часть 4 4. Дискуссия - Машина Гельмгольца и генеративная модель
Данная статья про машина гельмгольца подтверждают значимость применения современных методик для изучения данных проблем. Надеюсь, что теперь ты понял что такое машина гельмгольца, алгоритм бодрствования-сна и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Вычислительный интеллект
Комментарии
Оставить комментарий
Вычислительный интеллект
Термины: Вычислительный интеллект