Лекция
Привет, сегодня поговорим про теория нечетких систем, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое теория нечетких систем , настоятельно рекомендую прочитать все из категории Вычислительный интеллект.
Основным компонентом в процедурах нечеткого вывода является база правил нечетких продукций. В то же время существуют целые классы прикладных задач, в которых выявление и построение правил нечетких продукций невозможно или связано с серьезными трудностями концептуального характера. К таким задачам относятся задачи распознавания образов, экстраполяции и интерполяции функциональных зависимостей, классификации и прогнозирования, нелинейного и ситуационного управления, а также интеллектуального анализа данных (Data Mining).
Обшей особенностью подобных задач является существование некоторой зависимости или отношения, связывающего входные и выходные переменные модели системы, представляемой в форме так называемого «черного ящика». При этом выявление и определение данной зависимости в явном теоретико-множественном или аналитическом виде не представляется возможным либо по причине недостатка информации о моделируемой проблемной области, либо сложности учета многообразия факторов, оказывающих влияние на характер данной взаимосвязи.
Для конструктивного решения подобных задач разработан специальный математический аппарат, получивший название нейронных сетей. Достоинством моделей, построенных на основе нейронных сетей, является возможность получения новой информации о проблемной области в форме некоторого прогноза. При этом построение и настройка нейронных сетей осуществляется посредством их обучения на основе имеющейся и доступной информации.
Недостатком нейронных сетей является представление знаний о проблемной области в специальном виде, которое может существенно отличаться от возможной содержательной интерпретации существующих взаимосвязей и отношений.
Нечеткие нейронные сети или гибридные сети по замыслу их разработчиков призваны объединить в себе достоинства нейронных сетей и систем нечеткого вывода. С одной стороны, они позволяют разрабатывать и представлять модели систем в форме правил нечетких продукций, которые обладают наглядностью и простотой содержательной интерпретации. С другой стороны, для построения правил нечетких продукций используются методы нейронных сетей, что является более удобным и менее трудоемким процессом для системных аналитиков. В последнее время аппарат гибридных сетей повсеместно признается специалистами как один из наиболее перспективных для решения слабо или плохо структурированных задач прикладного системного анализа.
Наиболее важным применением теории нечетких множеств являются контроллеры нечеткой логики. Их функционирование несколько отличается от работы обычных контроллеров; для описания системы вместо дифференциальных уравнений используются знания экспертов. Эти знания могут быть выражены с помощью лингвистических переменных, которые описаны нечеткими множествами.
Понятие нечетких множеств (fuzzy sets) было введено в 1965 г. Л.Заде как обощение понятия классических множеств. В нечетком множестве каждый его элемент может принадлежать множеству частично, тогда как в классических множествах элемент или целиком принадлежит множеству, или нет. Степень принадлежности элемента a нечеткому множеству A характеризуется коэффициентом принадлежности , обозначаемому muA(a).
muA(a) - действительное число , принимающее значение в диапазоне (0,1), при этом 1 означает 100%-ю (безусловную) принадлежность a к множеству А, а 0 - безусловное отсутствие a в А.
Отображение множества элементов x во множество значений muA(x) образует функцию принадлежности muA(x).
Функция muA(x) может быть определена явно в виде, например, алгебраического выражения или таблично (дискретно) в виде массива пар
{x1/muA(x1), x2/muA(x2),...,xN/muA(xN)}.
В теории нечетких множеств помимо числовых переменных существуют переменные лингвистические. Например, лингвистичекая переменная "температура тела человека" может принимать значения: "пониженная", "нормальная", "повышенная", "высокая".
Нечеткое множество "нормальная температура тела" может быть дискретно задано следующим образом:
{36,2/0,15, 36,3/0,33, 36,4/0,6, 36,5/0,85, 36,6/1,0, 36,7/0,85, 36,8/0,6, 36,9/0,33, 37,0/0,15}.
То же множество может быть представлено следующим выражением:
muнорм=exp(-((t-36.6)/0.3)2).
На представленном ниже рисунке даны графики функций принадлежности для множеств, связанных с лингвистической переменной "температура тела человека".
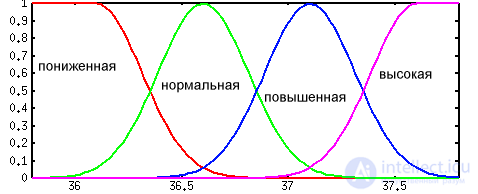
Носителем нечеткого множества A Supp(A) являются все элементы, для которых коэффициент принадлежности больше нуля, т.е. Supp(A)={x|muA(x)>0}. В приведенном выше примере табличного задания функции принадлежности носителем нечеткого множества "нормальная температура" является следующее множество:
{36,2, 36,3, 36,4, 36,5, 36,6, 36,7, 36,8, 36,9, 37,0}.
Два нечетких множества A и B равны между собой тогда и только тогда, когда muA(x)=muB(x) для всех элементов этих множеств.
Кардинальное число нечеткого множества A - сумма коэффициентов принадлежности всех элементов этого множества, т.е. M(A)=sum[i](muA(xi)).
Нечеткое множество называется нормальным, если хотя бы один его элемент имеет коэффициент принадлежности равный 1.
Сечением Aalpha нечеткого множества A называется подмножество элементов A, для которых muA(x)>alpha (слабое сечение) или muA(x)>=alpha (сильное сечение), при этом alpha принадлежит [0,1].
Основными операциями на нечетких множествах являются следующие.
Нечеткое множество A считается подмножеством нечеткого множества B, если для всех элементов A выполняется неравенство muA(x)<=muB(x).
Описанные выше операции на нечетких множествах обладают следующими свойствами:
Для определения степени нечеткости множества введено понятие меры нечеткости, сводящейся к измерению уровня различия между нечетким множеством A и его отрицанием ~A.
Наиболее популярна мера Е.Егера
FUZp(A)=1-Dp(A,~A)/(n1/p) ,
где n - количество элементов в A, Dp(A,~A) - расстояние между между множествами A и ~A в метрике p (p равно 1 или 2). Значение p=1 соответствует метрике Хемминга
D1(A,~A)=sum[i=1,n](|2*muA(xi)-1|) ,
а значение p=2 соответствует эвклидовой метрике
D2(A,~A)=(sum[i=1,n](2*muA(xi)-1)2)0,5 .
Другую меру нечеткости предложил Б.Коско, она основана на кардинальных числах множеств
FUZ(A)=M(AЛ~A)/M(AU~A).
В простейшем случае нечеткая продукция имеет следующий вид:
ЕСЛИ x это A, ТО y это B,
где A и B - значения лингвистических переменных, задаваемые функциями принадлежности. Левая часть продукции называется условием (или предпосылкой), а правая - следствием (или заключением). Продукцию часто в сокращенном виде записывают как A->B.
В более общем случае нечеткая продукция принимает такую форму:
ЕСЛИ x1 это A1 И ... Об этом говорит сайт https://intellect.icu . И xN это AN, ТО y это B,
Для вычисления значения коэффициента принадлежности сложного коньюнктивного условия продукции используются 2 способа:
Приписывание значения коэффициента принадлежности сложному условию продукции будем называть агрегированием условия.
Для вычисления коэффициента принадлежности продукции в целом также используется два способа:
Такой расчет значения функции принадлежности называется агрегированием на уровне продукции.
Продукционные системы с нечеткими продукциями называются нечеткими продукционными системами (ПС).
В технических и ряде других приложений в качестве входов x1, x2, ... ,xN и выхода y часто выступают доступные к измерению числовые величины. В такой ситуации для согласования нечетких продукций, оперирующих лингвистическими переменными, с входами/выходами в виде числовых значений в состав ПС вводятся так называемые фуззификатор и дефуззификатор. Фуззификатор преобразует множество входных данных в нечеткое множество, определяемое с помощью значений функции принадлежности, а дефуззификатор преобразует нечеткое множество, определяемое с помощью значений функции принадлежности, в конкретное значение.
Представленный ниже рис. упрощенно иллюстрирует функционирование нечеткой ПС Мамдани-Заде.
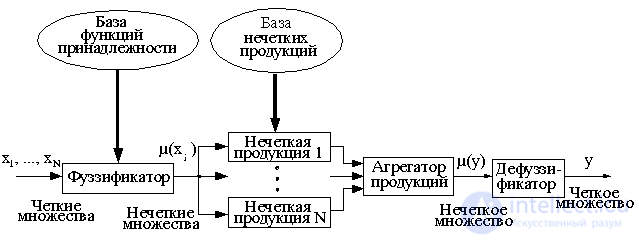
Поступившие на вход значения (например, результаты измерений на реальном физическом объекте) xi, i=1,2, ... , N, преобразуются в значения mu(xi) функций принадлежности нечетких множеств, с которыми оперирует ПС. Интепретатор ПС выбирает из базы нечетких продукций все применимые к входным данным продукции и определяет функции (???) принадлежности переменных y из правой части продукций. Поскольку в общем случае применимыми оказываются несколько продукций, то возникает проблема агрегирования функций принадлежности из правыхчастей отдельных продукций. Это объединение функций принадлежности реализуется, как правило, оператором логического сложения. Нечеткий результат в виде функции принадлежности mu(y) трансформируется дефуззификатором в конкретное значение выхода y.
Пример. Пусть на вход нечеткой ПС поступают 2 величины x1 и x2.Фуззификатор, используя базу функций принадлежности всех известных ему нечетких множеств, определяет значения коэффициентов принадлежности. Отличными от 0 оказались три коэффициента принадлежности muA1(x1)=0,5, muA2(x2)=0,25, muA3(x2)=0,75 для трех нечетких множеств A1, A2 и A3, как это показано ниже.
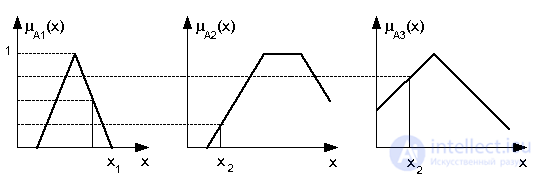
Далее интерпретатор выявил две применимые нечеткие продукции:
P1: ЕСЛИ x1 это A1 И x2 это A2, ТО y это B1,
P2: ЕСЛИ x1 это A1 И x2 это A3, ТО y это B2.
Для каждой из продукций в виде логического произведения выполняется агрегирование левой части (условия):
muИ1=min{muA1(x1), muA2(x2)}=0,25,
muИ2=min{muA1(x1), muA3(x2)}=0,5.
Затем выполняется агрегирование (опять же логическим произведением) на уровне продукций, как это показано на представленном ниже рисунке.
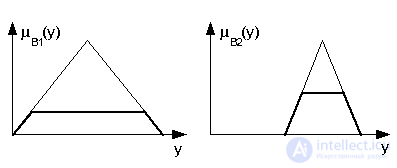
Результат агрегирования - функции принадлежности, графики которых выделены жирной линией.
Далее агрегатор продукций дает итоговую функцию принадлежности в виде логической суммы функций принадлежности отдельных продукций, как это показано на рисунке ниже.
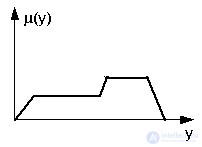
В конце концов дефуззификатор превращает итоговую функцию принадлежности в конкретное значение числовой величины y.
Фуззификатор осуществляет преобразование четкого множества X в нечеткое множество A, характеризующееся функцией принадлежности muA(x). Наибольшее распространение на практике получили функции принадлежности гауссова типа, а также треугольные и трапецеидальные функции.
Функция Гаусса для переменной x с центром c и параметром ширины s имеет следующий вид
muA(x)=exp(-((x-c)/s)2).
На представленном ниже рисунке даны графики этой функции для c=1 и s=1, 0,5, 0,25, 0,05.

Находит также применение обощенная гауссова функция в виде
muA(x)=exp(-(|x-c|/s)2*b),
где b - параметр формы. Ниже даны графики этой функции для c=1, s=1 и b=5, 2, 1, 0,6, 0,2.
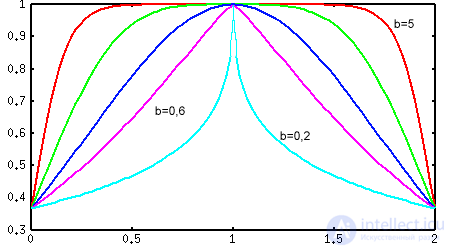
Легко заметить, что подбором параметра формы b обощенной функции Гаусса можно придать треугольную и трапецеидальную формы. Обобщенная функция Гаусса может быть также представлена в рациональной форме
muA(x)=1/(1+(|x-c|/s)2b).
Симметричная треугольная функция принадлежности может быть описана в виде
muA(x)=1-|x-c|/d для c-d<x<c+d,
muA(x)=0 для всех остальных x.
График треугольной функции принадлежности дан ниже.

Дефуззификатор преобразует нечеткое множество, заданное функцией принадлежности muA(x), в точечное решение. Для такого преобразования могут быть использованы многие способы, наиболее популярны следующие.
yс=int[y](y*mu(y)dy)/int[y](mu(y)dy).
или в дискретной формеyс=sum[i](yi*mu(yi))/sum[i](mu(yi)).
ya=sum[i](ci*mu(ci))/sum[i](mu(ci)),
где ci - центр i-ой одиночной функции принадлежности, участвующей в итоговой агрегированной функции.ym=sum[i](yi)/m,
где m - количество максимумов функции принадлежности, yi - значение, в котором функция принадлежности имеет максимум. Если mu(y) одинаковые максимальные значения на интервале между yl и yh, то yi=(yh+yl)/2.yl=min{yi},
где yi - значения, доставляющие функции принадлежности максимум.yh=max{yi},
На представленном ниже рисунке показано применение некоторых способов дефуззификации.
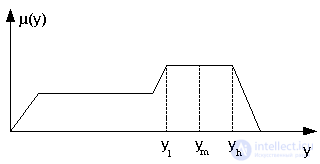
Результат, интересный с точки зрения пременения в нейронных сетях, может быть получен при использовании в нечеткой продукционной системы:
Обозначим через X=[x1, x2, ..., xN]T входной вектор. Пусть имеется M нечетких продукций вида
ЕСЛИ x1 это Ai1 И ... И xN это AiN, ТО y это Bi,
где i - номер продукции.
Тогда агрегирование алгебраическим произведением условий каждой продукции дает
prod[j=1:N](muAij(xj)).
Учитывая то, что для агрегирования относительно продукции используется логическое произведение (минимум из двух), и то, что muBi(ci)=1, где ci - это центр функции принадлежности нечеткого множества Bi из правой части продукции, в качестве значения функции принадлежности относительно i-ой продукции в целом также будем иметь
prod[j=1:N](muAij(xj)).
Дефуззификация относительно среднего центра дает
y=sum[i=1:M](ci*prod[j=1:N](muAij(xj)))/sum[i=1:M](prod[j=1:N](muAij(xj))).
При использовании для функций принадлежности всех множеств Aij обобщенной функции Гаусса в виде
muA(x)=exp(-(|x-c|/s)2b),
в итоге имеем
y = f(X) =
sum[i=1:M](ci*prod[j=1:N](exp(-((xj-cij)/sij)2bij)))
/ sum[i=1:M](prod[j=1:N](exp(-((xj-cij)/sij)2bij))).
где cij, sij и bij - центр, параметры ширины и формы функции принадлежности нечеткого множества Aij.
Доказано, что представленная непрерывная функция f(X) при соответствующем подборе параметров cij, sij, bij и ci может аппроксимировать заданную непрерывную функцию g(X) с произвольной точностью.
Ниже будет рассмотрена реализация полученного для f(X) выражения в виде многослойной нейронной сети, называемой нечеткой нейронной сетью.
Широкую популярность среди нечетких продукционных систем получила система Такаги-Сугено-Канга (TSK), продукции которой выглядят следущим образом:
ЕСЛИ x1 это Ai1 И ... И xN это AiN, ТО yi=fi(x1, ..., xN).
Поскольку в правых частях продукций определяются конкретные значения выходов yi, дефуззификатор на выходе системы не требуется.
Функция в правой части продукции - это, чаще всего, полином первой степени
yi=fi(X)=pi0+sum[j=1:N](pij*xj),
где pij - веса, подбираемые в процессе обучения продукционной системы.
При использовании M продукций итоговый выход y системы определяется как средневзвешенная сумма в виде
y = sum[i=1:M](wi*yi)/sum[i=1:M](wi)
= sum[i=1:M]((wi/sum[i=1:M](wi))*yi)
= sum[i=1:M](w'i*yi)
= sum[i=1:M](w'i*(pi0+sum[j=1:N](pij*xj))).
Для вычисления веса wi i-ой продукции в ПС используется агрегирование (в виде логического или алгебраического произведения) условий нечетких правил.
Если некоторые процессы объекта управления плохо поддаются формализации и математическому описанию, то в существующей системе управления используют фази-регулятор параллельно традиционному регулятору, т.е. нечеткая логика используется для замены традиционных алгоритмов управления и совместно с ними.
Экспериментально показано, что нечеткое управление дает лучшие результаты, по сравнению с получаемыми при классических алгоритмах управления. Очевидной областью внедрения алгоритмов нечеткой логики являются всевозможные экспертные системы, в том числе:
нелинейный контроль и управление в производстве (домна, робот, сушилка и т.д.);
самообучающиеся системы;
системы, распознающие тексты на естественном языке;
системы планирования и прогнозирования, опирающиеся на неполную информацию;
финансовый анализ в условиях неопределенности;
управление базами данных;
совершенствование стратегий управления и координации действий, например сложное промышленное производство.
Нечеткие числа, получаемые в результате “не вполне точных измерений”, во многом аналогичны распределениям теории вероятностей, но по сравнению с вероятностными методами, методы нечеткой логики позволяют резко сократить объем производимых вычислений, что, в свою очередь, приводит к увеличению быстродействия нечетких систем.
Недостатками нечетких систем являются:
отсутствие стандартной методики проектирования и расчета нечетких систем;
невозможность математического анализа нечетких систем существующими методами; применение нечеткого подхода по сравнению с вероятностным не приводит к повышению точности вычислений;
увеличение входных переменных увеличивает сложность вычислений экспоненциально;
как следствие предыдущего пункта, увеличивается база правил, что приводит к трудному ее восприятию.
При разработке нечетких систем необходимо пройти следующие этапы проектирования (после изучения основных понятий нечетких множеств и систем):
Определить входы и выходы создаваемой системы.
Задать для каждой из входных и выходных переменных функции принадлежности с термами.
Разработать базы правил выводов для реализуемой нечеткой системы.
Провести дефаззификацию.
Провести настройку и анализ адекватности разработанной модели реальной системе.
Программная реализация нечеткого регулятора на конкретном микроконтроллере.
Основанные на теории нечетких множеств методы построения компьютерных нечетких систем существенно расширяют области применения компьютеров. В последнее время нечеткое управление является одной из самых активных и результативных областей исследований применения теории нечетких множеств. Нечеткие методы помогают управлять домной и прокатным станом, автомобилем и поездом, распознавать речь и изображения, проектировать роботов, обладающих осязанием и зрением. Нечеткая логика, в основном, обеспечивает эффективные средства отображения неопределенностей и неточностей реального мира. Наличие математических средств отражения нечеткости исходной информации позволяет построить модель, адекватную реальности.
Перспективность данного направления исследований заключается в преимуществах Теории нечетких множеств при обработке нечетких данных, которыми изобилует реальная практика бизнеса и деятельность предприятий любой отрасли экономики в современных условиях.
Действительно, важной отличительной особенностью внешней среды предприятия является наличие рыночной неопределенности, поскольку на предприятие воздействуют неконтролируемые факторы внешней среды. В новых условиях, когда внешняя среда стала менее благоприятной, а конкуренция – более жесткой, роль научного подхода в решении актуальных задач управления деятельностью любого предприятия (фирмы, банка) резко возрастает.
Радикальные преобразования российской экономики привели к тому, что практически перед каждым предприятием встала проблема определения путей и способов адаптации к новым условиям функционирования. В современных условиях предприятие должно само определять и прогнозировать параметры внешней среды, ассортимент продукции и услуг, цены, поставщиков, рынки сбыта, свои долгосрочные цели и стратегию их достижения.
Неопределенность, присутствующая в задачах управления деятельностью любого предприятия (фирмы, банка), характеризуется размытостью используемых мнений и оценок экспертов, неполнотой и нечеткостью информации об основных параметрах и условиях анализируемой задачи, необходимостью учета степени отношения ЛПР к риску. Таким образом, неопределенность, приводящая к значительному повышению сложности задач управления деятельностью предприятия, порождается множеством факторов. Сочетание этих факторов на практике создает обширный спектр различных видов неопределенности.
Таким образом, все вышеизложенное позволяет сделать вывод, что неопределенность является отличительной особенностью различных задач управления деятельностью предприятия, а также фактором риска при принятии управленческих решений, поэтому необходимо учитывать ее для более адекватного отражения действительности. Очевидно, что в этой ситуации целесообразно применение формальных методов и современных информационных технологий.
Но возможности решения различных задач управления деятельностью предприятия, в силу их природной неопределенности, в рамках методов, пригодных к применению в условиях определенности или предположении о случайном характере переменных с известным законом распределения, ограничены, что в условиях неоднозначно определенных и качественных параметров, присущих рынку, дает в большинстве случаев неадекватное решение. Использование методов математической статистики затрудняется тем, что управленческие решения приходится принимать в условиях неопределенности, дефицита ресурсов, времени и информации, а практически каждая финансово-экономическая ситуация уникальна по своей природе, поэтому не удается с необходимым уровнем достоверности обосновать определенный закон распределения.
Коротко перечислим отличительные преимущества fuzzy-систем по сравнению с другими:
Применение нечетких систем
Что касается отечественного рынка коммерческих систем на основе нечеткой логики, то его формирование началось в середине 1995 года. Наиболее популярные у заказчиков следующие пакеты:
Основными потребителями нечеткой логики на рынке в постсоветских странах есть банкиры и финансисты, а также специалисты в области политического и экономического анализа. Они используют CubiCalc для создания моделей различных экономических, политических, биржевых ситуаций. Что же касается легкого в освоении пакета FuziCalc, то он занял свое место на компьютерах больших банкиров и специалистов по чрезвычайным ситуациям - то есть тех, для кого больше важна скорость проведения расчетов в условиях неполноты и неточности входной информации. Однако можно с уверенностью сказать, что эпоха расцвета прикладного использования нечеткой логики на отечественном рынке еще впереди.
Сегодня элементы нечеткой логики можно найти в десятках промышленных изделий - от систем управления электропоездами и боевыми вертолетами до пылесосов и стиральных машин. Рекламные кампании многих фирм (преимущественно японских) преподносят успехи в использовании нечеткой логики как особую конкурентное преимущество. Без применения нечеткой логики немыслимы современные ситуационные центры руководителей западных стран, в которых принимаются ключевые политические решения и моделируются различные кризисные ситуации. Одним из впечатляющих примеров масштабного применения нечеткой логики стало комплексное моделирование системы здравоохранения и социального обеспечения Великобритании (National Health Service - NHS), впервые позволило точно оценить и оптимизировать расходы на социальные нужды.
Не обошел средства нечеткой логики и программные системы, обслуживающих большой бизнес. Первыми, разумеется, были финансисты, задачи которых требуют ежедневного принятия правильных решений в сложных условиях непредвиденного рынка. Первый год использования системы Fuji Bank приносил банку в среднем $ 770000 в месяц (и это только официально объявлен прибыль!).
Вслед за финансистами, обеспокоенные успехами японцев и потерей стратегической инициативы, когнитивными нечеткими схемами заинтересовались промышленные гиганты США. Motorola, General Electric, Otis Elevator, Pacific Gas & Electric, Ford и другие в начале 90-х начали инвестировать в разработку изделий, использующих нечеткую логику. Имея солидную финансовую «поддержку», фирмы, специализирующиеся на нечеткой логике, получили возможность адаптировать свои разработки для широкого круга применений. «Оружие элиты» вышла на массовый рынок.
Среди лидеров нового рынка выделяется американская компания Hyper Logic, основанная в 1987 году Фредом Уоткинс (Fred Watkins). Сначала компания специализировалась на нейронных сетях, однако вскоре вполне сконцентрировалась на нечеткой логике. Недавно вышла на рынок вторая версия пакета CubiCalc фирмы HyperLogic, которая является одной из самых мощных экспертных систем на основе нечеткой логики. Пакет содержит интерактивную оболочку для разработки нечетких экспертных систем и систем управления, а также run-time модуль, позволяющий оформлять созданные пользователем системы в виде отдельных программ.
Кроме Hyper Logic среди «патриархов» нечеткой логики можно назвать такие фирмы как IntelligenceWare, InfraLogic, Aptronix. Всего же на мировом рынке представлено более 100 пакетов, которые тем или иным видом используют нечеткую логику. В трех десятках СУБД реализована функция нечеткого поиска. Собственные программы на основе нечеткой логики анонсировали такие гиганты как IBM, Oracle и другие.
На принципах нечеткой логики построен и один из российских программных продуктов - известный пакет «Бизнес-прогноз». Назначение этого пакета - оценка рисков и потенциальной доходности различных бизнес-планов, инвестиционных проектов и просто идей по развитию бизнеса. «Ведя» пользователя по сценарию его замысла, программа задает ряд вопросов, допускающих как точные количественные ответы, так и приближенные качественные оценки - типа «маловероятно», «степень риска высокий» и другие. Обобщив всю полученную информацию в виде единой схемы бизнес-проекта, программа не только выносит окончательный вердикт о рискованности проекта и ожидаемых прибылей, но и указывает критические точки и слабые места в авторском замысле. От аналогичных иностранных пакетов «Бизнес-прогноз» отличается простотой, дешевизной и, разумеется, русскоязычным интерфейсом.
К сожалению, в одной статье не просто дать все знания про теория нечетких систем. Но я - старался. Если ты проявишь интерес к раскрытию подробностей,я обязательно напишу продолжение! Надеюсь, что теперь ты понял что такое теория нечетких систем и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Вычислительный интеллект
Комментарии
Оставить комментарий
Вычислительный интеллект
Термины: Вычислительный интеллект