Нейронная сеть Хопфилда с гистерезисными двоичными нейронами кратко

Привет, Вы узнаете о том , что такое Нейронная сеть Хопфилда с гистерезисными двоичными нейронами, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое Нейронная сеть Хопфилда с гистерезисными двоичными нейронами , настоятельно рекомендую прочитать все из категории Вычислительный интеллект.

Нейронная сеть Хопфилда (англ. Hopfield network) — полносвязная нейронная сеть с симметричной матрицей связей. В процессе работы динамика таких сетей сходится (конвергирует) к одному из положений равновесия. Эти положения равновесия определяются заранее в процессе обучения, они являются локальными минимумами функционала, называемого энергией сети (в простейшем случае — локальными минимумами отрицательно определенной квадратичной формы на n-мерном кубе). Такая сеть может быть использована как автоассоциативная память, как фильтр, а также для решения некоторых задач оптимизации. В отличие от многих нейронных сетей, работающих до получения ответа через определенное количество тактов, сети Хопфилда работают до достижения равновесия, когда следующее состояние сети в точности равно предыдущему: начальное состояние является входным образом, а при равновесии получают выходной образ .

Ее вариацией является Нейронная сеть Хэмминга.

Нейронная сеть Хопфилда с нейронами с двойным порогом или нейронами со ступенчатым откликом привлекли значительный интерес как метод решения трудной проблемы оптимизации [8, 9]. Такефуджи и Ли предложили модель гистерезисного порога с двумя состояниями (бинарный) для подавления колебательного поведения сети нейронной динамики Хопфилда [10]. Однако, Татеми и Тамури показали, что модель Такефуджи и Ли не всегда гарантировала снижение энергетической функции [11]. Ванг также объяснил, почему модель может влиять на неточные результаты и колебательное поведение в процессе сходимости [12]. После их сообщения было предложено несколько модификаций гистерезисной функции, например двоичная Галана и Муньеза [13] и многозначная Бариткара и Менделя [14]. Смит и Портман показали, что простые «нейронные» сети оптимизации, описанные Тэнком и Хопфилдом, являлись эквивалентом схемы, содержащей триггеры Шмита с переменными порогами, и что гистерезис триггеров Шмита играл большую роль в определении стабильности [15, 16]. Архитектура
нейронной сети Хопфилда была также применена для контроля в режиме
реального времени координатных коммутаторов, используемых для
коммутации высокоскоростных пакетов на максимальной пропускной
способности, и было показано, что она способна достичь очень хорошего
исполнения особенно для проблем малоразмерных координатных
коммутаторов [17-21]. В статье «Двоичная нейронная сеть Хопфилда с
гистерезисом для больших координатных пакетных коммутаторов» авторов
Guangpu Xia, Zheng Tang, Yong Li, Jiahai Wang была представлена новая
архитектура нейронной сети Хопфилда для эффективного решения проблемы
координатного коммутатора. Об этом говорит сайт https://intellect.icu . В отличие от первоначальной нейронной сети
Хопфилда, предложенная архитектура использует гистерезисные двоичные
нейроны. Было теоретически доказано, что архитектура нейронной сети
Хопфилда с гистерезисными двоичными нейронами сходится как
первоначальная нейронная сеть Хопфилда. Для того, чтобы увидеть как
хорошо архитектура нейронной сети Хопфилда с гистерезисными двоичными
нейронами справляется с решением проблемы координатного коммутатора
было выполнено большое число компьютерных имитаций. Результаты
имитаций показывают, что архитектура нейронной сети Хопфилда с
гистерезисными двоичными нейронами гораздо лучше, чем предыдущие
работы, включая архитектуру нейронной сети Хопфилда, архитектуру
Траудета и максимальную нейронную сеть для проблемы координатных
коммутаторов, как с позиции времени вычислений, так и качества решений.
Как и первоначальная нейронная сеть Хопфилда, общий вход к нейрону
i нейронной сети Хопфилда с гистерезисными двоичными нейронами есть

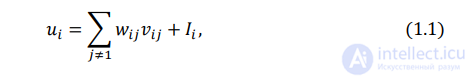
где

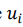есть общий вход нейрона i;
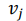– выход нейрона j;
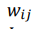– сила симметричного соединения от нейрона j к нейрону i;
– это компенсирующее смещение нейрона i.
Каждый нейрон вычисляет его выход по его входу. Но, в отличие от
нейронов нейронной сети Хопфилда с двумя состояниями порога (рисунок
1.5(а)), гистерезисные двоичные нейроны меняют значение их выхода или
оставляют его таким же согласно правилу гистерезисного порога (рисунок
1.5(б)):

где а – верхняя точка переключения (ВТП); b – нижняя точка переключения (НТП). Как показано на рисунке 1.5(б),

если 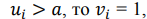, а если , 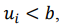то = .

Когда 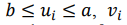удерживается неизменным, т.е. 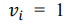если последнее было 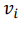1, и если последнее было 0.

Рисунок 1.5 – Функции активации: а) пороговая; б) гистерезисная

Рассмотрим энергию

Если wij = wji и wii = 0; изменение ΔE в энергии E благодаря
изменяющемуся состоянию нейрона i от 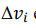есть

Используя уравнение 1.1 мы имеем:

Имеется два вида изменений в состоянии i-того нейрона, вызванных
корректировкой уравнения 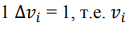, т.е. изменяется с 0 до 1.

Согласно правилу гистерезисного порога (уравнение 1.2), когда 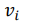изменяется с 0 до 1, мы имеем, что .

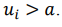Тогда

таким образом, энергия гарантированно уменьшится, если a > 0.

Из правила гистерезисного порога (уравнение 1.2), когда меняется с 1
до 0, мы имеем, что . Тогда

таким образом, энергия гарантированно уменьшится, если b ≤ 0.

Отсюда, сходимость энергетической функции к
локальному/глобальному минимуму всегда гарантирована только если 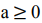и b ≤ 0.

Заметьте, что теоретические результаты представляли выдержку для первоначальной нейронной сети Хопфилда, в то время как первоначальная
сеть есть только один специальный случай при a = b = 0.

Более того, когда и b ≤ 0, абсолютное значение уменьшения энергии больше или как минимум такое же как и у первоначальной сети при каждом обновлении, таким образом, сеть с гистерезисными двоичными нейронами сходится к стабильному состоянию быстрее, чем оригинальная сеть.

Кроме того, несмотря на то, что выдержки теоретических результатов для однонаправленной нейронной сети Хопфилда, легко можно расширить их на
двух или даже больше направленные нейронные сети Хопфилда.

Рисунок 1.6 – Схематичная архитектура контроля координатного коммутатора 4 х 4

Литература

Вау!! 😲 Ты еще не читал? Это зря!

• архитектура нейронной сети ,
• сеть Хопфилда

Исследование, описанное в статье про Нейронная сеть Хопфилда с гистерезисными двоичными нейронами, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое Нейронная сеть Хопфилда с гистерезисными двоичными нейронами и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Вычислительный интеллект