АДАПТИВНЫЙ ГЕНЕТИЧЕСКИЙ АЛГОРИТМ ДЛЯ “МЯГКИХ” ЭВОЛЮЦИОННЫХ ВЫЧИСЛЕНИЙ кратко

Привет, сегодня поговорим про адаптивный генетический алгоритм для “мягких” эволюционных вычислений, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое адаптивный генетический алгоритм для “мягких” эволюционных вычислений , настоятельно рекомендую прочитать все из категории Вычислительный интеллект.

Введение.

В современном машиностроении и других отраслях народного хозяйства широкое распространение получили так называемые технологические процессы со слабосвязаннми подсистемами (ТПСП) и технологическое оборудование со слабосвязанными параметрами (ТОСП). Примером ТПСП может служить процесс заливки литейной формы, в котором температуры заполнения жидким металлом отдельных частей отливки связаны между собой общей температурой металла в струе из ковша, но эта связь не “жесткая”, — в разных частях (подсистемах) температуры могут отличаться на некоторую, ограниченную условиями процесса, величину. К объектам такого же класса относятся процессы многониточного резьбошлифования [1], многоручьевого непрерывного литья [2] и многие другое.

Постановка проблемы.

Проблемы в проектировании и управлении такими процессами возникают тогда, когда необходимо вычислить значения некоторых параметров-аргументов, доставляющих максимум (минимум) заданным целевым функциям, т.е. при решении задач оптимизации. Дело в том, что из-за сложности целевых функций в ТПСП и ТОСП аналитические методы оптимизации к ним неприменимы, а численные методы требуют поитерционного варьирования значений аргументов, что весьма затруднительно в условиях взаимной связи, в общем-то, функционально далеких друг от друга характеристик, относящихся к разным подсистемам.

Анализ последних достижений и публикаций.

В последнее время широкое распространение получил эволюционный метод оптимизации многоэкстремальных систем, названный генетическим алгоритмом (ГА) [3…5]. Как известно, основные вычисления в классическом ГА осуществляются на уровне так называемых “хромосом” — символьных моделей, несущих информацию об аргументах целевой функции. Если подсистемы в оптимизируемой системе независимы — целевые функции в них различны, а множества значений аргументов этих функций не пересекаются, то такие подсистемы с точки зрения рассматриваемой проблемы не связаны, и ее постановка распадается на несколько независимых задач классической оптимизации. Если же множества значений аргументов целевых функций в подсистемах пересекаются хотя бы частично, задача становится “жесткой”, т.к. варьируя связанные аргументы в одной подсистеме, мы невольно вынуждены одинаково варьировать их и в другой. Решать такие задачи предложено с помощью комплексного ГА, порождающего комплексные звездообразные хромосомы, учитывающие жесткие связи [6, 7]. В последнее время появились работы, вводящие новый вид хромосом — с “мягкой” связью аргументов, у которых связанные аргументы могут все-таки отличаться для двух подсистем, но не более, чем на некоторую величину Smax [8, 9]. Такое ограничение противоречит основному свойству ГА: свободному варьированию аргументов при решении задачи оптимизации. Действительно, на каждой эпохе эволюции ГА могут появляться хромосомы потомков, не удовлетворяющие указанному ограничению, что приводит к аварийному останову программы алгоритма. Появление таких потомков в относительно больших количествах (что и наблюдается на практике) делает даже комплексный ГА непригодным для оптимизационных вычислений. Это требует создания альтернативного ГА, содержащего в своем составе новый метод скрещивания хромосом, адаптирующийся к постоянно возникающим проблемам ограничений “мягкой” связности

Цель работы — повышение эффективности проектирования и управления за счет более глубокой оптимизации параметров объектов со слабосвязанными подсистемами путем разработки адаптивного генетического алгоритма для “мягких” эволюционных вычислений.

Основной материал. Об этом говорит сайт https://intellect.icu .

Основополагающим свойством ГА является то, что в процессе оптимизации аргументы могут принимать любые значения из области, ограниченной их минимальными и максимальными допустимыми значениями, например, для целевой функции N аргументов у(x); 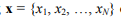область существования хромосом (область оптимизации) ограничена выражениями:

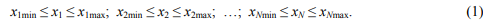
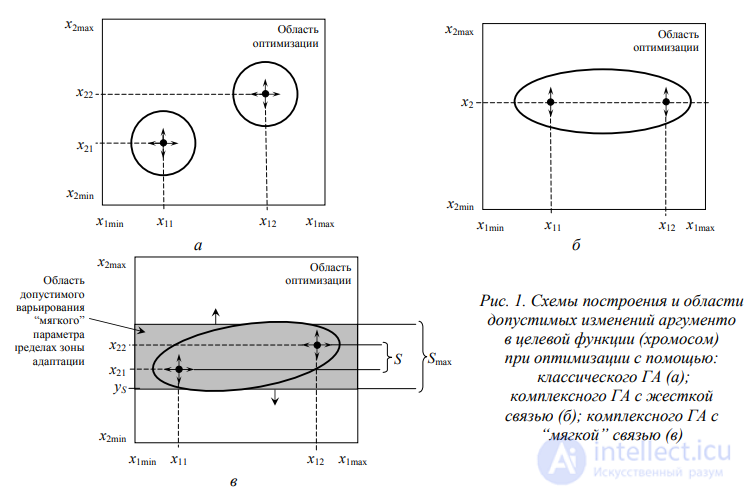
На рис. 1, а в качестве примера показаны две двухпараметрические несвязанные хромосомы двух подсистем одной системы, а также общая (совпадающая по всем аргументам) область допустимых значений для их четырех аргументов 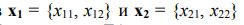в процессе оптимизации целевых функций 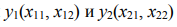с помощью ГА. В отличие от двух классических, при “жесткой” — математически строгой — связи одна комплексная хромосома несет информацию о трех аргументах: х11, х12 и х2, так как аргумент х2 у них общий (рис. 1, б). В то же время он сохраняет основное свойство ГА: свободное варьирование в пределах общих ограничений (1). При “мягкой” связи к ограничениям (1) добавляются новые:

для каждой группы связанных аргументов, состоящей, в общем случае, из 2, 3, …, N элементов. В соответствующей “мягкой” комплексной двухпараметрической хромосоме, как в первом случае, вновь хранятся четыре переменные: х11, х12, х21, х22, S (рис. 1, в), однако память такого ГА дополнительно содержит значение Smax для каждой “мягкой” связи.

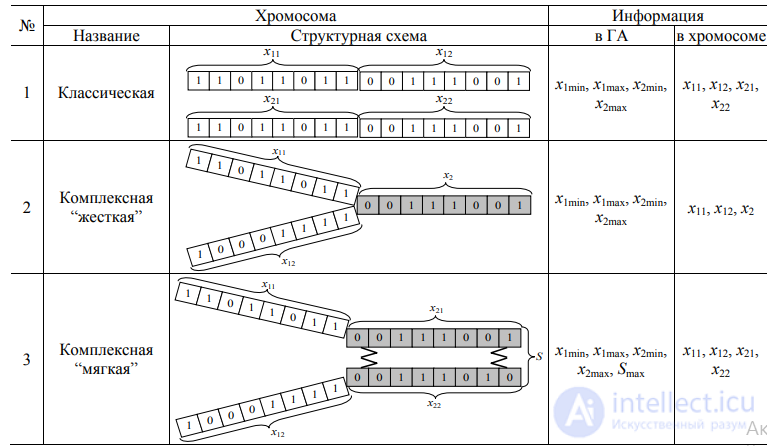
Структурные схема классической, а также комплексных “жесткой” и “мягкой” хромосом для случая двух аргументов, а также информация, содержащаяся в них и в памяти соответствующих ГА, приведены в таблице.

Схемы символьных моделей (хромосом) и содержащаяся в них информация для двух двухпараметрических подпроцессов

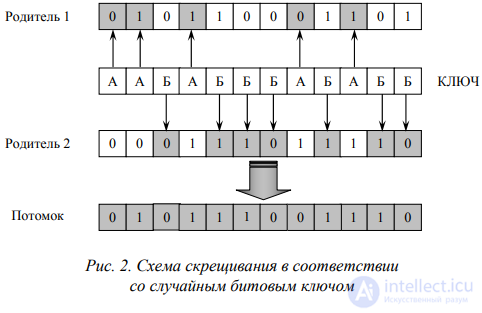
Адаптация алгоритма под оптимизацию объекта со слабосвязанными подсистемами осуществляли на этапе скрещивания ГА. В отличие от классического ГА, в котором чаще всего применяется точечное, двухточечное и многоточечное скрещивание, в комплексном ГА с “мягкими” связями применяли равномерное скрещивание, иначе называемое монолитным или одностадийным.

Такое скрещивание выполняется в соответствии со случайно выбранным битовым ключом, указывающим, какие гены должны наследоваться от первого, а какие от второго родителя. Допустим, что выбран эталон ААБАБББАБАББ, в котором А означает принятие гена на соответствующей позиции от первого родителя, а Б — от второго. Таким образом формируется первый потомок (рис. 2). Для второго потомка ключ считывается инверсивно: Б означает принятие гена на соответствующей позиции от первого родителя, а А — от второго

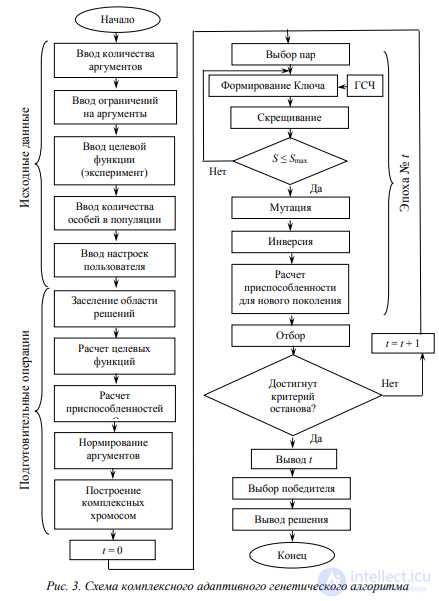
. Все полученные таким образом потомки подвергаются мутации и инверсии и далее проходят проверку на выполнение условия (2) и, если оно не выполняется, происходит повторное скрещивание тех же родителей, но при другом вновь случайно выбранном ключе. Эксперимент показывает, что “мягкой” операции скрещивания в сочетании с “жесткими” операциями мутации и инверсии достаточно для получения в приемлемое время потомков с соблюдением ограничений на связность. Если же таким образом не удается решить задачу, адаптивный подход можно распространить также и на мутацию с инверсией, что предоставит пользователю значительно больше возможностей выбора вариантов хромосом для потомков. Схема комплексного адаптивного генетического алгоритма приведена на рис. 3, она содержит блоки адаптации скрещивания, “следящие” за выполнением описанных выше ограничений на процесс оптимизации.

Работу адаптивного генетического алгоритма для “мягких” эволюционных вычислений испытывали в рамках САПР технологического процесса многоструйного непрерывного литья меди. В производстве установлено, что основным показателем качества получаемых при этом слитков является относительное удлинение металла δ в испытаниях на разрыв, а основные технологические характеристики, влияющие на δ, — средняя скорость вытягивания слитка V и температура охлаждающей воды на входе в кристаллизатор Т.

Из-за различного расположения кристаллизаторов относительно точки поступления жидкого металла в раздаточную печь для получения непрерывных отливок наилучшего качества параметры подпроцессов вытягивания и охлаждения для каждой из них должны отличаться, оставаясь в пределах ограничений связности. Расчеты выполняли для двух параллельно работающих кристаллизаторов, охлаждаемых от одного источника воды (связность по Т), из которых слитки извлекали однотипными вытягивающими устройствами (связность по V). Условия процесса позволяют варьировать параметры V и Т в пределах 3,2 ≤ V ≤ 3,6 м/мин и 20 ≤ Т ≤ 32 °С.

Из-за прерывистого режима вытягивания слитков и возникающих при этом низкочастотных колебаний функции δ1(V1, Т1) и δ2(V2, Т2) (индексы 1 и 2 относятся к разным кристаллизаторам) имеют многоэкстремальный характер. В этих условиях для расчетов был применен комплексный адаптивный ГА, что позволило рассчитать оптимальные параметры процесса: V1 = 3,37 м/мин; Т1 = 22 °С; V2 = 3,54 м/мин; Т2 = 29 °С.

Выводы. Предложенный метод оптимизации параметров объектов со слабосвязанными подсистемами, состоящий в применении разработанного адаптивного генетического алгоритма для “мягких” эволюционных вычислений, позволил повысить глубину оптимизации и получить в компьютерных экспериментах положительный технический эффект.

Литература

1. Тонконогий, В.М. Многоцелевая оптимизация методом комплексного генетического алгоритма / В.М. Тонконогий, А.А. Перпери, Д.А. Монова // Сучасні технології в машинобудуванні: зб. наук. пр. — Вип. 6. — Харків, НТУ “ХПІ”, 2011. — С. 276 — 281.

2. Прокопович, О.И. Температура поверхности катанки как косвенный параметр управления качеством / О.И. Прокопович, И.В. Прокопович, В.Д. Гогунский // Тр. Одес. политехн. ун-та. — Одесса, 2003. — Вып. 2(20). — С. 128 — 130.

3. Ротштейн, А.П. Интеллектуальные технологии идентификации: нечеткие множества, генетические алгоритмы, нейронные сети. — Винница: Универсум-Винница, 1999. — 320 с.

4. Скурихин, А.Н. Генетические алгоритмы // Новости искусственного интеллекта. — 1995. — № 4. — С. 6 — 46.

5. Змитрович, А.И. Интеллектуальные информационные системы. — Минск: Тетрасистемс, 1997. — 368 с.

6. Монова, Д.А. Комплексный генетический алгоритм / Д.А. Монова, А.А. Перпери, П.С. Швец // Пр. Одес. політехн. ун-ту. — Одеса, 2011. — Вип. 1(35). — С. 176 — 180

. 7. Перпері, А.О. Модернізація математичного методу генетичного алгоритму для оптимізації взаємозалежних технологічних процесів / А.О. Перпері, Л.А. Одукалець, Д.А. Монова, П.С. Швець // Моделювання та інформаційні технології: Зб. наук. пр. Ін-ту проблем моделювання в енергетиці ім. Г.Є. Пухова НАН України. — 2011. — Вип. 60. — С. 90 — 94.

8. Становский, А.Л. Эволюционная оптимизация слабосвязанных технических систем в САПР / А.Л. Становский, П.С. Швец, Д.А. Желдубовский // Пр. Одес. політехн. ун-ту. — 2011. — Вип. 2(36). — С. 234 — 238.

9. Становский, А.Л. Оптимизация слабосвязанных систем в автоматизированном проектировании и управлении / А.Л. Становский, П.С. Швец, И.Н. Щедров. // Сучасні технології в машинобудуванні: зб. наук. пр. — Вип. 6. — Харків, НТУ “ХПІ”, 2011. — С. 129 — 134.

К сожалению, в одной статье не просто дать все знания про адаптивный генетический алгоритм для “мягких” эволюционных вычислений. Но я - старался. Если ты проявишь интерес к раскрытию подробностей,я обязательно напишу продолжение! Надеюсь, что теперь ты понял что такое адаптивный генетический алгоритм для “мягких” эволюционных вычислений и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Вычислительный интеллект