Лекция
Привет, Вы узнаете о том , что такое сеть кохонена, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое сеть кохонена, самоорганизующиеся карты кохонена, self-organizing map, som, упругая карта , настоятельно рекомендую прочитать все из категории Вычислительный интеллект.
А сегодня мы поговорим об еще одном типе сетей под названием сети Кохонена, которые также называют картами Кохонена. Нам предстоит разобраться, каков принцип их работы, какие цели они призваны реализовывать, в общем, нас сегодня интересует все, что касается нейронных сетей Кохонена
Самоорганизующаяся карта Кохонена (англ. self-organizing map — SOM) — нейронная сеть с обучением без учителя, выполняющая задачу визуализации и кластеризации. Идея сети предложена финским ученым Т. Кохоненом. Является методом проецирования многомерного пространства в пространство с более низкой размерностью (чаще всего, двумерное), применяется также для решения задач моделирования, прогнозирования, выявление наборов независимых признаков, поиска закономерностей в больших массивах данных, разработке компьютерных игр, квантизации цветов к их ограниченному числу индексов в цветовой палитре: при печати на принтере и ранее на ПК или же на приставках с дисплеем с пониженным числом цветов, для архиваторов [общего назначения] или видео-кодеков, и прч. Является одной из версий нейронных сетей Кохонена.
Метод был предложен финским ученым Теуво Кохоненом в 1984 году. Существует множество модификаций исходной модели.
Итак, давайте для начал обсудим, какие же задачи должны выполнять нейронные сети Кохонена. Основным их назначением является кластеризация образцов, то есть разделение образцов на группы (кластеры) по тем или иным признакам. Например, перед нами может стоять задача классификации спортсменов по виду спорта, которым они занимаются. Тут подходящими признаками могут быть рост, вес, время, за которое спортсмен пробегает стометровку и т. д. =) Если пропустить «параметры» всех спортсменов через сеть кохонена , то на выходе мы получим определенное количество групп, при этом должны выполняться следующие условия:
В данном примере все спортсмены, занимающиеся легко атлетикой попадут в одну группу, а баскетболисты в другую. При дальнейшем обучении сети от группы легкоатлетов может отделиться группа бегунов. И тогда, следя второму из перечисленных свойств, группа бегунов должна располагаться близко к группе легкоатлетов и далеко от группы баскетболистов. Вот так в общих чертах и работают сети данного типа
Нейронная сеть Кохонена в отличие от рассмотренных нами ранее сетей обучается без учителя и носит название самоорганизующейся карты Кохонена (SOFM — Self-Organizing Feature Map). Давайте познакомимся с ее структурой поближе.
Карты Кохонена имеют набор входных элементов, количество которых совпадает с размерностью подаваемых на вход векторов, и набор выходных элементов, каждый их которых соответствует одному кластеру (группе). Если мы анализируем спортсменов по 4 признакам — скорость бега, рост, вес, выносливость, то, соответственно, мы должны иметь 4 входа, по одному для каждого признака. В этом случае в качестве входного вектора выступает один из спортсменов, а его координатами являются значения его признаков. Не знаю, удачную ли я выбрал аналогию, но надеюсь, что на таких примерах станет понятнее суть работы самоорганизующихся карт Кохонена )
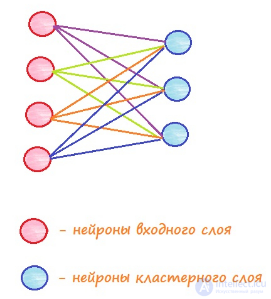
Обычно стараются задавать количество выходных элементов меньшим, чем количество входных, в таком случае сеть позволяет позволяет получить упрощенную характеристику объектов для дальнейшей работы с ними.
Также необходимо остановить на структуре связей между элементами сети. Тут все просто — каждый входной элемент соединяется с каждым выходным, и все связи, также как и для других нейронных сетей, имеют определенный вес, который корректируется в процессе обучения.
Но прежде, чем переходить к обсуждению тонкостей обучения сетей Кохонена, давайте разберемся, как вообще сеть должна работать…
При подаче какого-либо вектора на вход сеть должна определить, к какому из кластеров этот вектор ближе всего. В качестве критерия близости может быть выбран критерий минимальности квадрата евклидова расстояния. Рассмотрим входной вектор как точку в n-мерном пространстве (n — количество координат вектора, это число равно числу входных нейронов, как мы обсуждали ранее). Тогда нам нужно вычислить расстояние между этой точкой и центрами разных кластеров и определить, расстояние до какого из кластеров окажется минимальным. Тогда этот кластер (и соответствующий ему выходной нейрон) объявляется победителем.
А какая же точка является центром кластера и какие у нее координаты в этом пространстве? Тут все очень изящно =) Координатами центра кластера являются величины весов всех связей, которые приходят к данному выходному нейрону от входных элементов. Поскольку каждый выходной нейрон (кластер) соединен с каждым входным нейроном, то мы получаем, n связей, то есть n координат для точки, соответствующей центру кластера. Формула для вычисления квадрата евклидова расстояния выглядит следующим образом:
Здесь — квадрат расстояния между точкой P и кластером K. Координаты точки P —
, а координаты центра кластера K —
.
Таким образом, подав вектор на вход сети мы получим один кластер-победитель, соответственно, этот вектор будет принадлежать именно к этому кластеру (группе). Именно так карты Кохонена решают задачу классификации.
Давайте теперь перейдем к процессу обучения, ведь прежде чем сеть начнет правильно группировать элементы в кластеры, необходимо ее обучить.
Суть обучения состоит в следующем. На вход подается вектор из обучающей выборки. Для этого вектора определяется кластер-победитель, и для этого кластера производят коррекцию весовых коэффициентов таким образом, чтобы он оказался еще ближе ко входному вектору. Чаще всего также корректируют веса нескольких соседей кластера-победителя.
В отличие от обучения с учителем, рассмотренного ранее, суть обучения состоит не в том, чтобы сравнивать вывод сети с идеальным выводом, а в подстройке весов всех связей для максимального совпадения со входными данными.
Для корректировки весов используется следующая формула:
В этой формуле — вес на шаге t+1, а
— вес на шаге t (то есть на предыдущем).
— норма обучения, а
— координата входного вектора. Обратите внимание, что норма обучения также зависит от номера шага и меняется в процессе обучения. Кроме того, меняется и радиус, определяющий какое количество элементов сети будут подвергнуты корректировке весов. Давайте разберем поподробнее, что определяет это радиус.
Выходные (кластерные) элементы сети Кохонена обычно представляют расположенными тем или иным образом в двумерном пространстве. Разместим, к примеру, выходные элементы в виде квадратной сетки и зададим начальный радиус обучения равным 2. Подаем на вход сети вектор и элементом-победителем оказывается нейрон, обозначенный на схеме красным цветом. По алгоритму обучения мы должны обновить значения весов для этого нейрона, а также для тех, которые попадают в круг заданного радиуса (в данном случае 2) — эти элементы выделены зеленым.
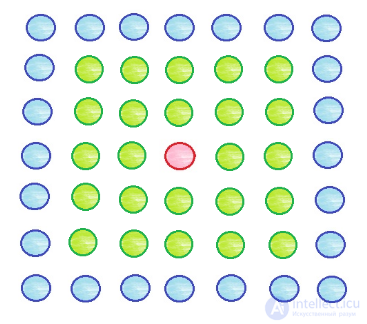
Ближе к концу процесса обучения радиус уменьшается. Пусть он стал равным единице, тогда обновляться будут веса следующих элементов:
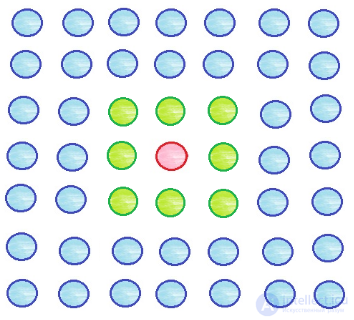
Итак, разобрав все составляющие процесса обучение давайте напишем конкретный алгоритм для этого процесса:
Остановка обучения происходит в том случае, если величины изменения весов становятся очень маленькими.
На этом моменте предлагаю сегодня остановиться, поскольку статья получилась довольно большой ) Мы обязательно продолжим изучать карты Кохонена в следующей статье!
Продолжаем работать с самоорганизующимися картами Кохонена, а точнее продолжаем изучать принципы их функционирования и обучения.
Итак, приступаем к делу…
Первую часть мы закончили на том, что разобрали алгоритм обучения сети Кохонена. Давайте рассмотрим небольшой пример, наглядно демонстрирующий протекание данного процесса.
Рассмотрим сеть, имеющую 2 входных элемента и 25 выходных.
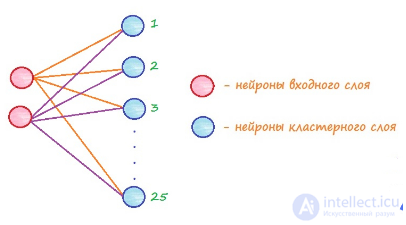
Зададим для каждого кластера веса связей равными некоторым значениям, близким к 0.5. Как мы обсуждали в предыдущей статье весовые значения являются координатами кластеров, а поскольку в данном случае мы имеем две координаты, то есть двумерное пространство, то мы легко можем изобразить все кластеры на графике:
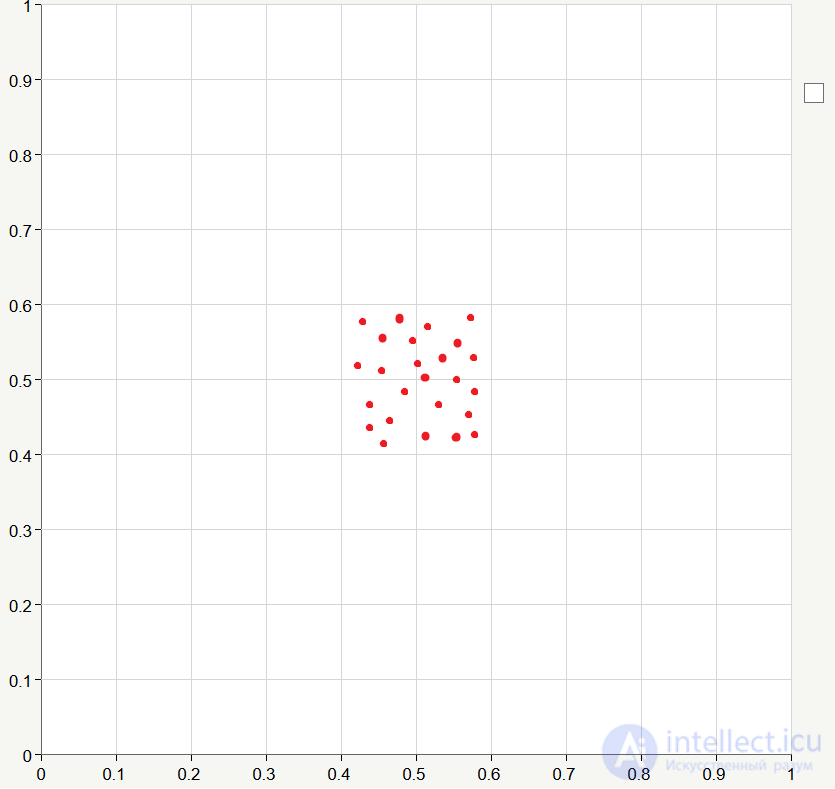
Пусть обучающие данные будут сгенерированы случайным образом в диапазоне от 0 до 1:

Итак, у нас есть сеть, есть начальные значения коэффициентов связей, есть обучающая последовательность, так давайте же проведем обучение =) В отличие от обучения с учителем при обучении сети Кохонена обучающая выборка подается на вход не один, а много раз. Один полный проход обучающей выборки называют эпохой. Вот так может выглядеть наша сеть после 20-30 эпох обучения (я соединил линиями соседние кластеры):
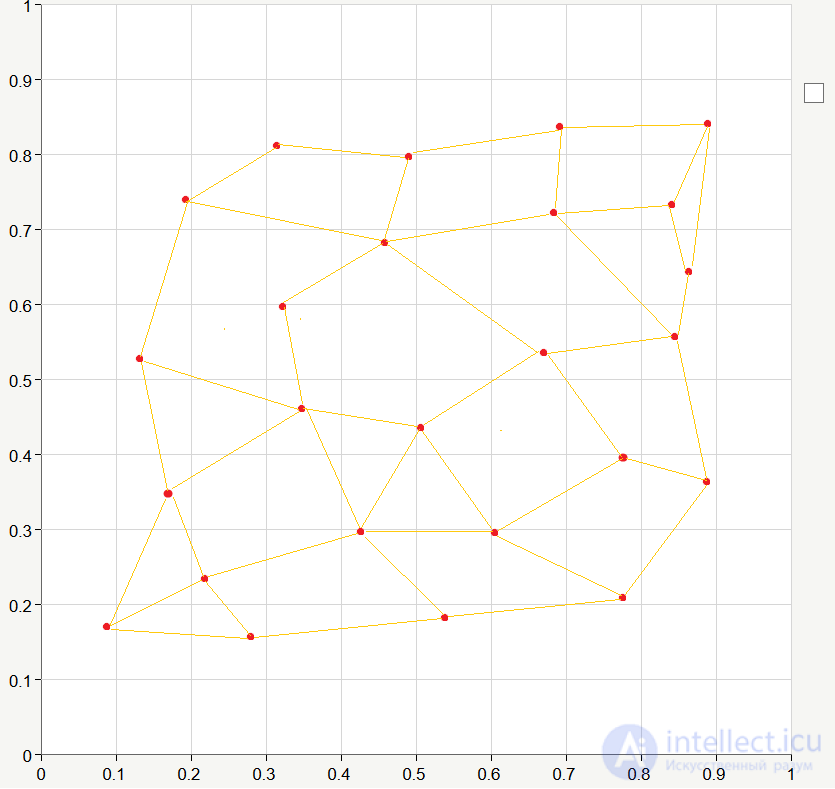
Как видите сеть «растягивается». Продолжим обучение, и после 200 эпох сеть может принять следующий вид:
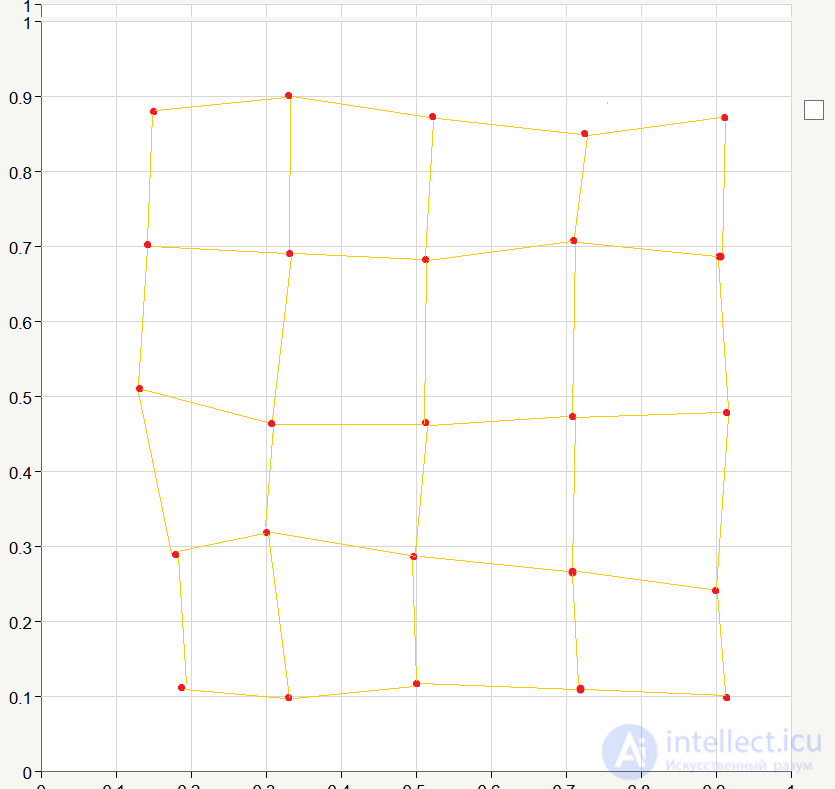
В итоге получаем довольно-таки упорядоченное расположение нейронов. Это объясняется тем, что входные элементы мы взяли случайным образом и они более менее равномерно распределены в квадрате, соответствующем координатам от 0 до 1. Естественно, на практике мы вряд ли получили бы такой идеальный вариант, но суть процесса обучения этот пример описывает очень хорошо ) Для достижения «идеальности» при реальном обучении необходимо очень удачно выбрать начальные веса связей, которые мы в нашем теоретическом примере задали случайным образом.
На самом деле рассмотренная сеть не очень подходит для решения реальных задач, поскольку в большинстве случаев при использовании карт Кохонена стремятся получить более простую характеристику данных, чем изначальная. То есть число выходных элементов выбирают меньшим, чем число входных признаков.
Существуют специальные программы, которые позволяют моделировать нейронные сети, в частности сети Кохонена. При желании можно написать и свою собственную программу для решения подобный задач и графического отображения результатов Я нашел в интернете более менее наглядный пример работы такой программы и хочу привести здесь, чтобы можно было получить представление о том, как все это работает и используется на практике.
Пусть у нас есть сеть, принимающая на вход 20 признаков, а выходные нейроны представляют собой сеть 12*16, как на этом рисунке: 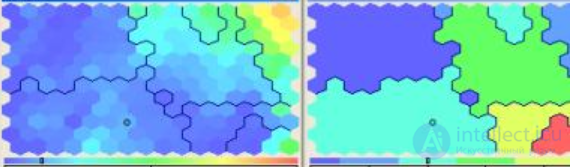
Левая часть изображения представляет собой входную карту для одного из признаков. Желтый и красный цвета соответствуют максимальным значениям признака, а синий — минимальным. Исходя из картинки мы можем сделать вывод, что входные элементы, имеющие значения исследуемого признака близкие к максимальному будут отнесены к кластерам, находящимся в правом верхнем углу.
Такие входные карты можно построить для любого из 20 входных признаков.
Правая часть картинки — выходная карта, то есть наша сеть определила, что изначальные кластеры (12*16 штук) можно объединить так, как указано на изображении. То есть в итоге мы получим 7 различных групп, к которым могут быть отнесены подаваемые на вход элементы. Возможно, на первый взгляд, все это кажется довольно-таки непонятным, а может и бессмысленным, но на самом деле все это устроено очень логично и красиво =)
На этой ноте мы заканчиваем сегодняшнюю статью, надеюсь, что мне удалось раскрыть тему самоорганизующихся карт Кохонена, так что до скорых встреч!
Самоорганизующаяся карта состоит из компонентов, называемых узлами или нейронами. Их количество задается аналитиком. Каждый из узлов описывается двумя векторами. Первый — т. н. вектор веса m, имеющий такую же размерность, что и входные данные. Второй — вектор r, представляющий собой координаты узла на карте. Карта Кохонена визуально отображается с помощью ячеек прямоугольной или шестиугольной формы; последняя применяется чаще, поскольку в этом случае расстояния между центрами смежных ячеек одинаковы, что повышает корректность визуализации карты.
Изначально известна размерность входных данных, по ней некоторым образом строится первоначальный вариант карты. В процессе обучения векторы веса узлов приближаются к входным данным. Для каждого наблюдения (семпла) выбирается наиболее похожий по вектору веса узел, и значение его вектора веса приближается к наблюдению. Также к наблюдению приближаются векторы веса нескольких узлов, расположенных рядом, таким образом если в множестве входных данных два наблюдения были схожи, на карте им будут соответствовать близкие узлы. Циклический процесс обучения, перебирающий входные данные, заканчивается по достижении картой допустимой (заранее заданной аналитиком) погрешности, или по совершении заданного количества итераций. Таким образом, в результате обучения карта Кохонена классифицирует входные данные на кластеры и визуально отображает многомерные входные данные в двумерной плоскости, распределяя векторы близких признаков в соседние ячейки и раскрашивая их в зависимости от анализируемых параметров нейронов.
В результате работы алгоритма получаются следующие карты:
Наиболее распространены три способа задания первоначальных весов узлов:
Пусть — номер итерации (инициализация соответствует номеру 0).
,
для любого , где
— вектор веса узла
. Если находится несколько узлов, удовлетворяющих условию, BMU выбирается случайным образом среди них.
Функция определяет «меру соседства» узлов и
и изменение векторов веса. Она должна постепенно уточнять их значения, сначала у большего количества узлов и сильнее, потом у меньшего и слабее. Часто в качестве функции соседства используется гауссовская функция:
где — обучающий сомножитель, монотонно убывающий с каждой последующей итерацией (то есть определяющий приближение значения векторов веса BMU и его соседей к наблюдению; чем больше шаг, тем меньше уточнение);
,
— координаты узлов
и
на карте;
— сомножитель, уменьшающий количество соседей с итерациями, монотонно убывает.
Параметры ,
и их характер убывания задаются аналитиком.
Более простой способ задания функции соседства:
,
если находится в окрестности
заранее заданного аналитиком радиуса, и 0 в противном случае.
Функция равна
для BMU и уменьшается с удалением от BMU.
Изменить вектор веса по формуле:
Т.о. Об этом говорит сайт https://intellect.icu . вектора веса всех узлов, являющихся соседями BMU, приближаются к рассматриваемому наблюдению.
Например, как среднее арифметическое расстояний между наблюдениями и векторами веса соответствующих им BMU:
,
где N — количество элементов набора входных данных.
Устойчивость к зашумленным данным, быстрое и неуправляемое обучение, возможность упрощения многомерных входных данных с помощью визуализации.
Самоорганизующиеся карты Кохонена могут быть использованы для кластерного анализа только в том случае, если заранее известно число кластеров .
Важным недостатком является то, что окончательный результат работы нейронных сетей зависит от начальных установок сети. С другой стороны, нейронные сети теоретически могут аппроксимировать любую непрерывную функцию, что позволяет исследователю не принимать заранее какие-либо гипотезы относительно модели .
Задача векторного квантования состоит, по своему существу, в наилучшей аппроксимации всей совокупности векторов данных кодовыми векторами
. Самоорганизующиеся карты Кохонена также аппроксимируют данные, однако при наличии дополнительной структуры в совокупности кодовых векторов (англ. codebook). Предполагается, что априори задана некоторая симметричная таблица «мер соседства» (или «мер близости») узлов: для каждой пары
(
) определено число
(
) при этом диагональные элементы таблицы близости равны единице (
).
Векторы входных сигналов обрабатываются по одному, для каждого из них находится ближайший кодовый вектор («победитель», который «забирает все»)
. После этого все кодовые векторы
, для которых
, пересчитываются по формуле
где — шаг обучения. Соседи кодового вектора — победителя (по априорно заданной таблице близости) сдвигаются в ту же сторону, что и этот вектор, пропорционально мере близости.
Чаще всего, таблица кодовых векторов представляется в виде фрагмента квадратной решетки на плоскости, а мера близости определяется, исходя из евклидового расстояния на плоскости.
Самоорганизующиеся карты Кохонена служат, в первую очередь, для визуализации и первоначального («разведывательного») анализа данных . Каждая точка данных отображается соответствующим кодовым вектором из решетки. Так получают представление данных на плоскости («карту данных»). На этой карте возможно отображение многих слоев: количество данных, попадающих в узлы (то есть «плотность данных»), различные функции данных и так далее. При отображении этих слоев полезен аппарат географических информационных систем (ГИС). В ГИС подложкой для изображения информационных слоев служит географическая карта. Карта данных является подложкой для произвольного по своей природе набора данных. Карта данных служит заменой географической карте там, где географической карты просто не существует. Принципиальное отличие в следующем: на географической карте соседние объекты обладают близкими географическими координатами, на карте данных близкие объекты обладают близкими свойствами. С помощью карты данных можно визуализировать данные, одновременно нанося на подложку сопровождающую информацию (подписи, аннотации, атрибуты, информационные раскраски) . Карта служит также информационной моделью данных. С ее помощью можно заполнять пробелы в данных. Эта способность используется, например, для решения задач прогнозирования.
Идея самоорганизующихся карт очень привлекательна и породила массу обобщений, однако, строго говоря, мы не знаем, что мы строим: карта — это результат работы алгоритма и не имеет отдельного («объектного») определения. Есть, однако, близкая теоретическая идея — главные многообразия (англ. principal manifolds) . Эти многообразия обобщают линейные главные компоненты. Они были введены как линии или поверхности, проходящие через «середину» распределения данных, с помощью условия самосогласованности: каждая точка на главном многообразии
является условным математическим ожиданием тех векторов
, которые проектируются на
(при условии
, где
— оператор проектирования окрестности
на
),
Самоорганизующиеся карты могут рассматриваться как аппроксимации главных многообразий и популярны в этом качестве .
Метод аппроксимации многомерных данных, основанный на минимизации «энергии упругой деформации» карты, погруженной в пространство данных, был предложен А. Н. Горбанем в 1996 году, и впоследствии развит им совместно с А. Ю. Зиновьевым, А. А. Россиевым и А. А. Питенко . Метод основан на аналогии между главным многообразием и эластичной мембраной и упругой пластиной. В этом смысле он является развитием классической идеи сплайна (хотя упругие карты и не являются многомерными сплайнами).
Пусть задана совокупность входных векторов . Так же, как и сети векторного квантования и самоорганизующиеся карты,
упругая карта представлена как совокупность кодовых векторов (узлов)
в пространстве сигналов. Множество данных
разделено на классы
, состоящие из тех точек
, которые ближе к
, чем к другим
(
). Искажение кодирования
может трактоваться как суммарная энергия пружин единичной жесткости, связывающих векторы данных с соответствующими кодовыми векторами.
На множестве узлов задана дополнительная структура: некоторые пары связаны «упругими связями», а некоторые тройки объединены в «ребра жесткости». Обозначим множество пар, связанных упругими связями, через , а множество троек, составляющих ребра жесткости, через
. Например, в квадратной решетке ближайшие узлы (как по вертикали, так и погоризонтали) связываются упругими связями, а ребра жесткости образуются вертикальными и горизонтальными тройками ближайших узлов. Энергия деформации карты состоит из двух слагаемых:
энергия растяжения
энергия изгиба
где — соответствующие модули упругости.
Задача построения упругой карты состоит в минимизации функционала
Если разбиение совокупности входных векторов на классы
фиксировано, то минимизация
— линейная задача с разреженной матрицей коэффициентов. Поэтому, как и для сетей векторного квантования, применяется метод расщепления: фиксируем
— ищем
— для данных
ищем
— для данных
ищем
— … Алгоритм сходится к (локальному) минимуму
.
Метод упругих карт позволяет решать все задачи, которые решают самоорганизующиеся карты Кохонена, однако обладает большей регулярностью и предсказуемостью. При увеличении модуля изгиба упругие карты приближаются к линейным главным компонентам. При уменьшении обоих модулей упругости они превращаются в Кохоненовские сети векторного квантования. В настоящее время упругие карты интенсивно используются для анализа многомерных данных в биоинформатике.[10] Соответствующее программное обеспечение опубликовано и свободно доступно на сайте института Кюри (Париж)[11][12].
На рисунке представлены результаты визуализации данных по раку молочной железы. Эти данные содержат 286 примеров с указанием уровня экспрессии 17816 генов[13]. Они доступны онлайн как ставший классическим тестовый пример для визуализации и картографии данных[14].
Нейронные сети Кохонена — класс нейронных сетей, основным элементом которых является слой Кохонена. Слой Кохонена состоит из адаптивных линейных сумматоров («линейных формальных нейронов»). Как правило, выходные сигналы слоя Кохонена обрабатываются по правилу «Победитель получает все»: наибольший сигнал превращается в единичный, остальные обращаются в ноль.
По способам настройки входных весов сумматоров и по решаемым задачам различают много разновидностей сетей Кохонена . Наиболее известные из них:
Слой Кохонена состоит из некоторого количества параллельно действующих линейных элементов. Все они имеют одинаковое число входов
и получают на свои входы один и тот же вектор входных сигналов
. На выходе
го линейного элемента получаем сигнал
где:
После прохождения слоя линейных элементов сигналы посылаются на обработку по правилу «победитель забирает все»: среди выходных сигналов выполняется поиск максимального ; его номер
. Окончательно, на выходе сигнал с номером
равен единице, остальные — нулю. Если максимум одновременно достигается для нескольких
, то:
«Нейроны Кохонена можно воспринимать как набор электрических лампочек, так что для любого входного вектора загорается одна из них» .
Большое распространение получили слои Кохонена, построенные следующим образом: каждому (-му) нейрону сопоставляется точка
в
-мерном пространстве (пространстве сигналов). Для входного вектора
вычисляются его евклидовы расстояния
до точек
и «ближайший получает все» — тот нейрон, для которого это расстояние минимально, выдает единицу, остальные — нули. Следует заметить, что для сравнения расстояний достаточно вычислять линейную функцию сигнала:
(здесь — Евклидова длина вектора:
). Последнее слагаемое
одинаково для всех нейронов, поэтому для нахождения ближайшей точки оно не нужно. Задача сводится к поиску номера наибольшего из значений линейных функций:
Таким образом, координаты точки совпадают с весами линейного нейрона слоя Кохонена (при этом значение порогового коэффициента
).
Если заданы точки , то
-мерное пространство разбивается на соответствующие многогранники Вороного-Дирихле
: многогранник
состоит из точек, которые ближе к
, чем к другим
(
) .
Задача векторного квантования с кодовыми векторами
для заданной совокупности входных векторов
ставится как задача минимизации искажения при кодировании, то есть при замещении каждого вектора из
соответствующим кодовым вектором. В базовом варианте сетей Кохонена используется метод наименьших квадратов и искажение
вычисляется по формуле
где состоит из тех точек
, которые ближе к
, чем к другим
(
). Другими словами,
состоит из тех точек
, которые кодируются кодовым вектором
.
Если совокупность задана и хранится в памяти, то стандартным выбором в обучении соответствующей сети Кохонена является метод K-средних. Это метод расщепления:
где — число элементов в
.
Далее итерируем. Этот метод расщепления сходится за конечное число шагов и дает локальный минимум искажения.
Если же, например, совокупность заранее не задана, или по каким-либо причинам не хранится в памяти, то широко используется онлайн метод. Векторы входных сигналов
обрабатываются по одному, для каждого из них находится ближайший кодовый вектор («победитель», который «забирает все»)
. После этого данный кодовый вектор пересчитывается по формуле
где — шаг обучения. Остальные кодовые векторы на этом шаге не изменяются.
Для обеспечения стабильности используется онлайн метод с затухающей скоростью обучения: если — количество шагов обучения, то полагают
. Функцию
выбирают таким образом, чтобы
монотонно при
и чтобы ряд
расходился, например,
.
Векторное квантование является намного более общей операцией, чем кластеризация, поскольку кластеры должны быть разделены между собой, тогда как совокупности для разных кодовых векторов
не обязательно представляют собой раздельные кластеры. С другой стороны, при наличии разделяющихся кластеров векторное квантование может находить их и по-разному кодировать.
Решается задача классификации. Число классов может быть любым. Изложим алгоритм для двух классов, и
. Исходно для обучения системы поступают данные, класс которых известен. Задача: найти для класса
некоторое количество
кодовых векторов
, а для класса
некоторое (возможно другое) количество
кодовых векторов
таким образом, чтобы итоговая сеть Кохонена с
кодовыми векторами
,
(объединяем оба семейства) осуществляла классификацию по следующему решающему правилу:
если для вектора входных сигналов ближайший кодовый вектор («победитель», который в слое Кохонена «забирает все») принадлежит семейству
, то
принадлежит классу
; если же ближайший к
кодовый вектор принадлежит семейству
, то
принадлежит классу
.
С каждым кодовым вектором объединенного семейства связан многогранник Вороного-Дирихле. Обозначим эти многогранники
,
соответственно. Класс
в пространстве сигналов, согласно решающему правилу, соответствует объединению
, а класс
соответствует объединению
. Геометрия таких объединений многогранников может быть весьма сложной (см. рисунок с примером возможного разбиения на классы).
Правила обучения сети онлайн строится на основе базового правила обучения сети векторного квантования. Пусть на вход системы подается вектор сигналов , класс которого известен. Если он классифицируется системой правильно, то соответствующий
кодовый вектор
слегка сдвигается в сторону вектора сигнала («поощрение»)
Если же классифицируется неправильно, то соответствующий
кодовый вектор
слегка сдвигается в противоположную сторону от сигнала («наказание»)
где — шаг обучения. Для обеспечения стабильности используется онлайн метод с затухающей скоростью обучения. Возможно также использование разных шагов для «поощрения» правильного решения и для «наказания» неправильного.
Это — простейшая (базовая) версия метода[15]. Существует множество других модификаций.
Прочтение данной статьи про сеть кохонена позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое сеть кохонена, самоорганизующиеся карты кохонена, self-organizing map, som, упругая карта и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Вычислительный интеллект
Комментарии
Оставить комментарий
Вычислительный интеллект
Термины: Вычислительный интеллект