Лекция
Привет, Вы узнаете о том , что такое аффинные преобразования, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое аффинные преобразования, маштабирование, поворот , настоятельно рекомендую прочитать все из категории Компьютерная графика.
2.1 Координатный метод
Координатный метод был введен в XVII веке французскими математиками Р. Декартом и П. Ферма. На этом методе основывается аналитическая геометрия, которую можно считать фундаментом КГ. В современной КГ координатный метод широко используется.
2.1.1. Преобразование координат Сначала рассмотрим общие вопросы преобразования координат. Пусть задана п-мерная система координат в базисе (k1, k2,.... kn), которая описывает положение точки в пространстве с помощью числовых значений кi. В КГ наиболее часто используются двумерная (n = 2) и трехмерная (n = 3) системы координат. Если задать другую, N-мерную, систему координат в базисе (m1, m2,..., т) и поставить задачу определения координат в новой системе, зная координаты в старой, то решение (если оно существует) можно записать в таком виде:
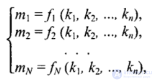
где fi — функция пересчета i-й координаты, аргументами являются координаты в системе ki,. Можно поставить и обратную задачу: по известным координатам (m1, m2,.... т) определить координаты (к1, k2,..., кn ). Решение обратной задачи запишем так:
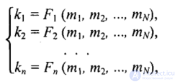
где Fi — функции обратного преобразования. В случае если размерности систем координат не совпадают (п ≠ N), осуществить однозначное преобразование координат чаще всего не удается. Например, по двумерным экранным координатам нельзя без дополнительных условий однозначно определить трехмерные координаты отображаемых объектов. Линейные преобразования наглядно записываются в матричной форме:
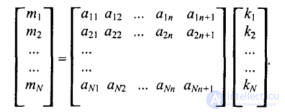
Здесь матрица коэффициентов (аij) умножается на матрицу-столбец (ki), и в результате будем иметь матрицу-столбец (mi )
Мы и дальше часто будем использовать умножение матриц, поэтому сделаем небольшой экскурс в матричную алгебру. Для двух матриц —
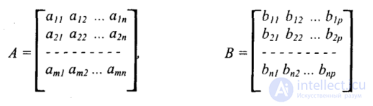
матрицы А размерами (т х п) и В — (n x p): матричным произведением является матрица С = АВ размерами (m х р):
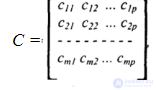
С = для которой элементы cij рассчитываются по формуле

Простейшие двумерные преобразования
Точки на xy-плоскости можно перенести в новые позиции путем добавления к координатам этих точек констант переноса. Для каждой точки Р(х, у), которая перемещается в новую точку Р'(х, у), сдвигаясь на Dx единиц параллельно оси x и на Dy единиц параллельно оси у, можно написать уравнения:
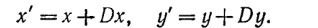
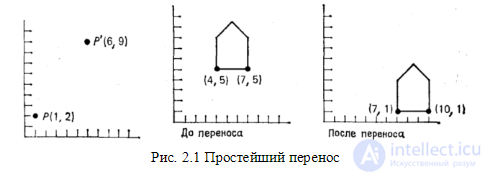
На рис. 2.1 показана точка с координатами (1, 2), которая смещается на расстояние (5, 7), преобразуясь в точку (6, 9). Определяя векторы-строки
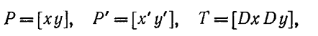
можно переписать это уравнение в векторной форме или более кратко
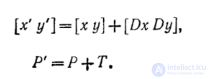
Объект можно перенести, применяя вышевыведенное уравнения к каждой его точке. Однако, поскольку каждый отрезок, описывающий объект, состоит из бесконечного числа точек, такой процесс длился бы бесконечно долго. К счастью, все точки, принадлежащие отрезку, можно перенести путем перемещения одних лишь крайних точек отрезка и последующего вычерчивания нового отрезка между получившимися в результате точками. Это справедливо также для масштабирования (растяжения) и поворот а. На рис. 2.1 показан результат действия на контур домика операции переноса на расстояние (3, -4)
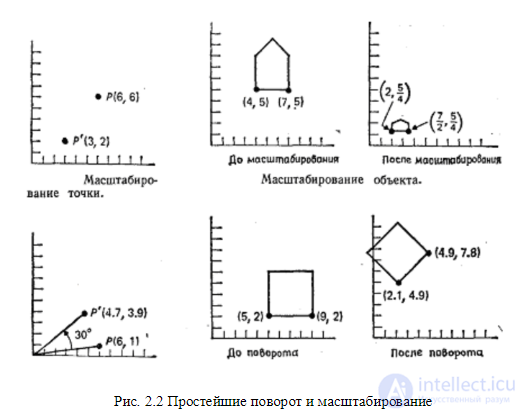
Точки можно промасштабировать (растянуть) в Sx раз вдоль оси x: и в Sy раз вдоль оси у, получив в результате новые точки, с помощью умножения Определяя S как , можно записать в матричной форме или На рис. 2.2 отдельная точка (6, 6) масштабируется с коэффициентами 1/2 по оси X и 1/3 по оси у. На этом же рисунке показан контур домика, промасштабированный с коэффициентами 1/2 по оси x и 1/4 по оси у. Отметим, что масштабирование производится относительно начала координат; в результате преобразования домик стал меньше и ближе к началу координат. Если бы масштабные множители были больше 1, то домик увеличился бы и отдалился от начала координат. Способы проведения масштабирования относительно других точек, отличных от начала координат, рассматриваются в одном из последующих разделов главы. Пропорции домика также изменились· было применено неоднородное масштабирование, при котором Sх≠ Sу. Однородное масштабирование, для которого Sx=Sy, не влияет на пропорции. Точки могут быть повернуты на угол θ относительно начала координат, как показано на рис. 2.2 для точки Ρ (6, 1) и угла θ = 30°. Математически поворот определяется следующим образом: В матричной форме мы имеем или где через R обозначена матрица поворота. На рис. 2.2 показан квадрат, повернутый на 45°. Как и в случае масштабирования, поворот производится относительно начала координат.
Однородные координаты и матричное представление двумерных преобразований Преобразования переноса, масштабирования и поворота в матричной форме записываются в виде К сожалению, перенос реализуется отдельно (с помощью сложения) от масштабирования и поворота (с помощью умножения). Хотелось бы представить их таким способом, чтобы все эти три элементарных преобразования можно было легко объединять вместе. Ниже в этом разделе показано, как это можно сделать. Если мы выразим точки в однородных координатах, то все три преобразования можно реализовать с помощью умножений. Однородные координаты были введены в геометрии и впоследствии использованы в графике. С однородными координатами и преобразованиями над ними работают многие пакеты графических подпрограмм и некоторые дисплейные процессоры. В одних случаях эти координаты используются прикладной программой непосредственно при задании параметров для графического пакета, в других — применяются лишь внутри самого пакета и недоступны для программиста. В однородных координатах точка Р (х, у) записывается как P(W∙ x, W ∙ y, W) для любого масштабного множителя W≠0. При этом если для точки задано ее представление в однородных координатах Р(Х, Y, W), то можно найти ее двумерные декартовы координаты как x=X/W и y=Y/W. В этой главе W всегда будет равно 1, поэтому операция деления не требуется. Однородные координаты можно представить как вложение промасштабированной с коэффициентом W двумерной плоскости в плоскость z=W (здесь z = 1) в трехмерном пространстве. Точки теперь описываются трехэлементными вектор-строками, поэтому матрицы преобразований, на которые умножается вектор точки, чтобы получить другой вектор точки, должны иметь размер 3x3. Уравнения переноса записываются в виде матрицы преобразования однородных координат следующим образом:
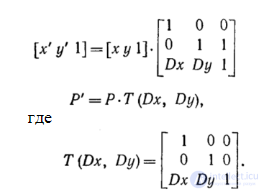
Что будет, если точку Ρ перенести в точку Р' на расстояние (Dx1, Dy1), а затем в Р" на расстояние (Dx2 Dy2). Интуитивно ожидаемый результат в этом случае представляет собой суммарный перенос на расстояние (Dx1+Dx2, Dy1+Dy2). Чтобы доказать это, запишем данные в виде Теперь получим: Матричное произведение Τ(Dx1, Dy1) ∙ T(Dx2, Dy2) есть Действительно, результирующий перенос есть (Dx1+Dx2, Dy1+ Dy2). Матричное произведение в разных случаях называют объединением, соединением, конкатенацией и композицией матриц T(Dx1, Dy2) и T(Dx2, Dy2). В этой главе мы будем использовать термин композиция. Уравнения масштабирования в матричной форме записываются в виде Определяя имеем Так же как последовательные переносы являются аддитивными, можно ожидать, что последовательные масштабирования будут мультипликативными. Если заданы то получим: Матричное произведение S(Sx1, Sy1)∙S(Sx2, Sy2) есть Таким образом, масштабирования в самом деле мультипликативны. И, наконец, уравнения поворота можно представить в виде:

Композиция двумерных преобразований
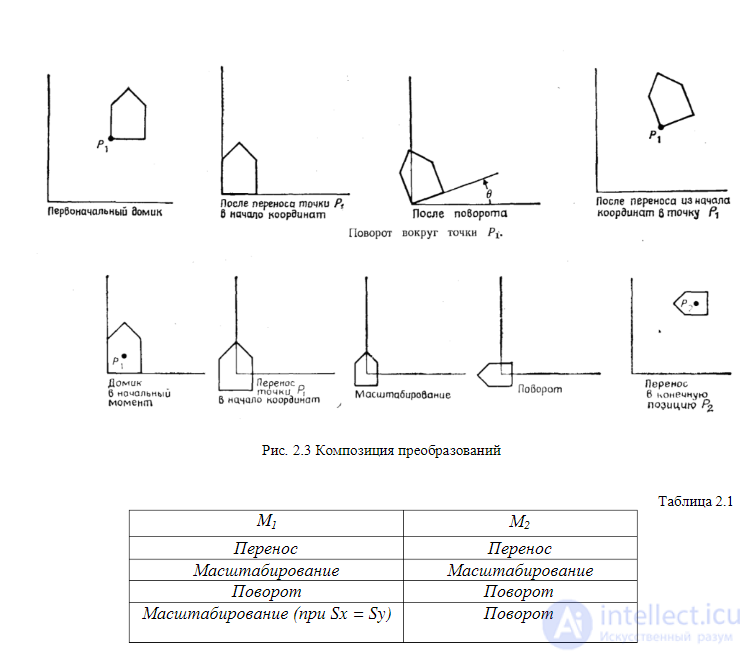
Понятие композиции было введено в предыдущем разделе. В данном разделе мы покажем, каким образом можно использовать композицию преобразований для объединения фундаментальных матриц R, S и Τ с целью получения желаемых общих результатов. Основное преимущество объединенных преобразований состоит в том, что к точке более эффективно применять одно результирующее преобразование, чем ряд преобразований друг за другом. Рассмотрим, например, поворот объекта относительно некоторой произвольной точки Pi. Поскольку нам известно, лишь как поворачивать вокруг начала координат, разобьем исходную (трудную) проблему на три более легкие задачи. Таким образом, чтобы произвести поворот относительно точки Pi, необходимо выполнить последовательно три элементарных преобразования: 1. Перенос, при котором точка Pi перемещается в начало координат. 2. Поворот. 3. Перенос, при котором точка из начала координат возвращается в первоначальное положение Ρi. Эта последовательность показана на рис. 2.3, на котором вокруг точки Ρi(x, у) поворачивается контур домика. Первый перенос производится на (-x1, -y1), в то время как последующий — на (x1, y1) — является обратным ему.
Результат существенно отличается от того, который получился бы, если бы применялся один только поворот. Результирующее преобразование имеет вид
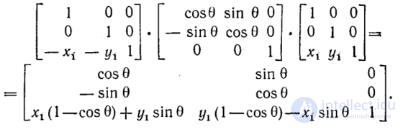
Эта композиция преобразований путем умножения матриц служит примером того, как применение однородных координат упрощает задачу. Об этом говорит сайт https://intellect.icu . Используя аналогичный подход, можно промасштабировать объект относительно произвольной точки Рi: перенести Ρi в начало координат, промасштабировать, перенести назад в точку Ρi. Результирующее преобразование в этом случае будет иметь вид
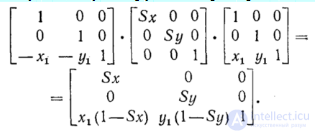
Предположим, что нам необходимо промасштабировать, повернуть и расположить в нужном месте домик, показанный на рис.2.3, где центром поворота и масштабирования является точка Ρ1. Последовательность преобразований заключается в переносе точки Ρ1 в начало координат, проведении масштабирования и поворота, а затем переносе из начала координат в новую позицию Р2, в которой домик должен оказаться (эта последовательность показана на рис. 2.3). В структуре данных, в которой содержится это преобразование, могут находиться масштабный множитель (множители), угол поворота и величины переноса или может быть записана матрица результирующего преобразования:
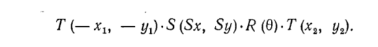
Если известно, что M1 и M2 представляют собой элементарные перенос, масштабирование или поворот, то при каких условиях Μ1 и Μ2 коммутативны? В общем случае умножение матриц некоммутативно. Однако легко показать, что в следующих частных случаях коммутативность имеет место (в этих случаях можно не беспокоиться о порядке перемножения матриц – см. Таблицу 2.1).
Матричное представление трехмерных преобразований
Аналогично тому, как двумерные преобразования описываются матрицами размером 3x3, трехмерные преобразования могут быть представлены в виде матриц размером 4x4. И тогда трехмерная точка (x, у, z) записывается в однородных координатах как (W∙x, W∙y, W∙z, W), где W≠0. Если W≠1, для получения трехмерных декартовых координат точки (х, у, z) первые три однородные координаты делятся на W. Отсюда, в частности, следует, что две точки Η1 и H2 в пространстве однородных координат описывают одну и ту же точку трехмерного пространства в том и только в том случае, когда H1=cH2 для любой константы с, не равной нулю. Трехмерная система координат, применяемая в этой книге, является правосторонней (рис.2.4). Примем соглашение, в соответствии с которым положительными будем считать такие повороты, при которых (если смотреть с конца положительной полуоси в направлении начала координат) поворот на 90° против часовой стрелки будет переводить одну положительную полуось в другую. На основе этого соглашения строится следующая таблица, которую можно использовать как для правых, так и для левых систем координат
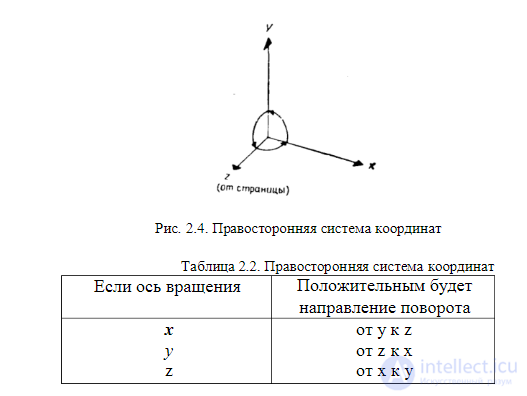
Мы применяем здесь правостороннюю систему координат, поскольку она хорошо знакома большинству людей, хотя в трехмерной графике чаще более удобна левосторонняя система, так как ее легче представить наложенной на поверхность экрана дисплея. Это позволяет естественно интерпретировать тот факт, что точки с большими значениями z находятся дальше от наблюдателя. Отметим, что в левосторонней системе положительными будут повороты, выполняемые по часовой стрелке, если смотреть с конца положительной полуоси в направлении начала координат. Трехмерный перенос является простым расширением двумерного:
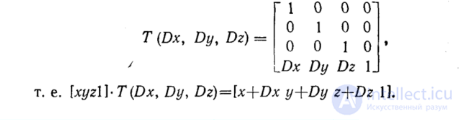
Масштабирование расширяется аналогичным образом:
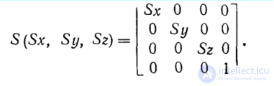
В самом деле, Двумерный поворот является в то же время трехмерным поворотом вокруг оси z. В трехмерном пространстве поворот вокруг оси z описывается выражением Это легко проверить: в результате поворота на 90° вектора [1 0 0 1], являющегося единичным вектором оси х, должен получиться единичный вектор [0 1 0 1] оси y. Вычисляя произведение получаем предсказанный результат [0 1 0 1]. Матрица поворота вокруг оси x имеет вид Матрица поворота вокруг оси у записывается в виде Столбцы (и строки) верхней левой подматрицы размером 3x3 матриц Rz, Rx и Ry представляют собой взаимно ортогональные единичные векторы, интерпретация которых такая же, что и в двумерном случае. Все эти матрицы преобразований имеют обратные матрицы. Матрица, обратная Т, получается подстановкой знака минус перед Dx, Dy и Dz; обратная S — заменой Sx, Sy и Sz на обратные им значения, а для каждой из трех матриц поворота — выбором отрицательного угла поворота.
Композиция трехмерных преобразований
Путем объединения элементарных трехмерных преобразований можно получить другие преобразования. В этом разделе показано, как это сделать. Задача состоит в том, чтобы преобразовать отрезки P1P2 и P1P3 (рис. 2.5) из начальной позиции в конечную. Точка Pi переносится в начало координат, P1P2 располагается вдоль отрицательной полуоси x, а P1P3 помещается в плоскости yz в той ее половине, где ось у положительна. На длины отрезков преобразование не воздействует. Как и прежде, разобьем сложную задачу на более простые. В данном случае преобразование можно выполнить за четыре шага: 1. Перенос точки Pi в начало координат. 2. Поворот вокруг оси у до совмещения P1P2 с плоскостью уz. 3. Поворот вокруг оси x до совмещения P1P2 с отрицательной полуосью Z. 4. Поворот вокруг оси z до совмещения P1P3 с плоскостью yz. Шаг 1. Перенос Ρ1 в начало координат:
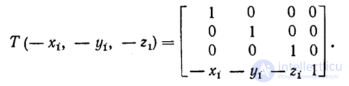
Применение Τ к P1, Р2 и Р3 дает Шаг 2. Поворот вокруг оси у. На рис. 2.5 показаны отрезки P1P2 после шага 1 и проекция P1P2 на плоскость xz. Поворот производится на положительный угол θ, для которого где Тогда Как и ожидалось, x-компонента Р2 равна нулю. Шаг 3. Поворот вокруг оси х. На рис. 2.6 показан отрезок P1P2 Рис. 2.5. Композиция преобразований после шага 2. Поворот производится на отрицательный угол φ, для которого где Запись обозначает длину Результатом поворота на шаге 3 является т. е. теперь совпадает с отрицательной полуосью z. Шаг 4. Поворот вокруг оси z. На рис. 2.6 показаны и после шага 3, когда Р2'" лежит на отрицательной полуоси z, а Р3'" - в точке Поворот производится на положительный угол , для которого Шаг 4 является последним шагом, после которого получается конечный результат, показанный на рис. 2.6. Результирующая матрица
описывает искомое преобразование, где Рис. 2.6. Окончание композиции преобразований Преобразование объектов Преобразование объектов можно описать так. Пусть любая точка, принадлежащая определенному объекту, имеет координаты (k1, k2,..., kn ) в n-мерной системе координат. Тогда преобразование объекта можно определить как изменение положения точек объекта. Новое положение точки пространства соответствует новым значениям координат (т1, т2,..., тn). Соотношение между старыми и новыми координатами для всех точек объекта (т1, т2,..., тn) = F(k1, k2,..., kn ) и будет определять преобразование объекта, где F—функция преобразования. Классифицировать преобразования объектов можно согласно типу функции преобразования и типу системы координат. Например, преобразование объектов на плоскости можно определить так: В трехмерном пространстве: Преобразование как изменение систем координат Мы рассматриваем преобразование множества точек, принадлежащих объекту, в некоторое другое множество точек, причем оба этих множества описаны в одной и той же системе координат. Таким образом, система координат остается неизменной, а сам объект преобразуется относительно начала координат до получения желаемого размера. Другим эквивалентным способом описания преобразования является смена систем координат. Такой подход оказывается полезным, когда желательно собрать вместе много объектов, каждый из которых описан в своей собственной локальной системе координат, и выразить их координаты в одной глобальной системе координат. Существует и еще один, третий подход, при котром происходит изменение глобальной системы координат по отношению к локальной системе координат объекта (см. рис.2.7)
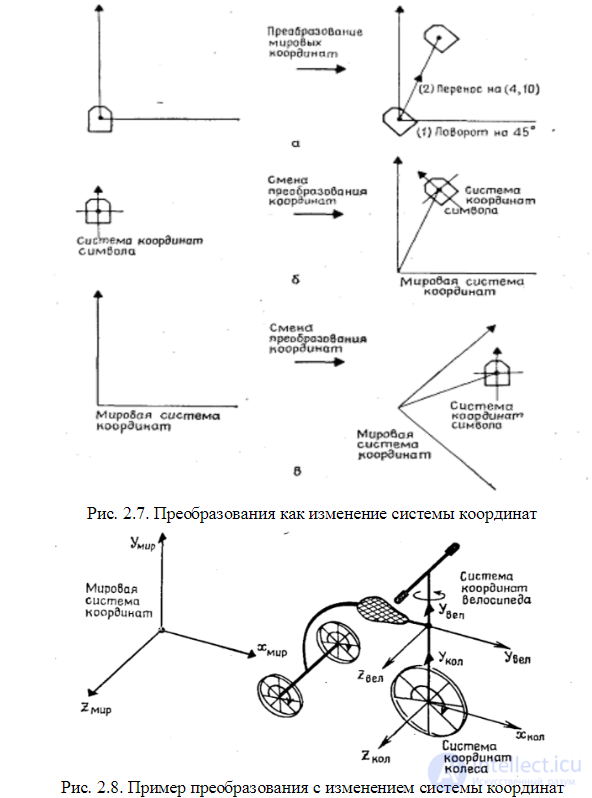
Описание всех объектов (символов) в мировой системе координат и последующее размещение их в желаемом месте, приводит до некоторой степени к нереалистичному изображению всех символов, первоначально заданных один поверх другого в одной и той же мировой системе координат. Более естественно полагать, что каждый символ задан в своей собственной системе координат и затем промасштабирован, повернут и перенесен путем преобразования координат в новую мировую систему координат. Второй подход легко представить себе как сжатие или растяжение, поворот и позиционирование на мировой координатной плоскости отдельных листков бумаги, на каждом из которых изображен символ (или наоборот, сжатие или растяжение, поворот и перемещение плоскости относительно каждого из листков бумаги). С математической точки зрения оба подхода идентичны. Подход, основанный на изменении систем координат, удобен в тех случаях, когда задается дополнительная информация для подобъектов в их локальных системах координат. Например, если к переднему колесу трехколесного велосипеда (рис. 2.8) приложить крутящий момент, то все его колеса повернутся. Нам необходимо определить, насколько велосипед переместится в пространстве как единое целое. Эта задача более сложная, чем та, которая связана с размещением символов, поскольку здесь требуется несколько последовательных изменений систем координат. В начальный момент системы координат велосипеда и его переднего колеса заданы относительно мировой системы
координат. При движении велосипеда вперед переднее колесо поворачивается вокруг оси z системы координат колеса, и одновременно системы координат колеса и велосипеда перемещаются относительно мировой системы координат. Системы координат колеса и велосипеда связаны с мировой системой координат с помощью зависящих от времени переносов вдоль осей x и у и поворота вокруг оси у. Координатные системы велосипеда и колеса между собой связаны с помощью зависящего от времени поворота вокруг оси у, вызываемого поворотом руля. (Система координат велосипеда связана с рамой велосипеда, а не с рулем). 2.1.2 аффинные преобразования на плоскости Это частный случай преобразований, который достаточно часто используется при создании графических пакетов. Зададим некоторую двумерную систему координат (x,у). Аффинное преобразование на плоскости описывается формулами где А, В,..., F— константы. Значение (X, Y) можно рассматривать как координаты в новой системе координат. Обратное преобразование (X, Y) в (х, у) также является аффинным: Аффинное преобразование удобно записывать в матричном виде. Константы А, В..... F образуют матрицу преобразования, которая, будучи умноженной на матрицу-столбец координат (x, у), дает матрицу-столбец (X, Y). Однако, чтобы учесть константы С и F, необходимо перейти к так называемым однородным координатам — прибавим еще одну строку в матрицах координат: Теперь рассмотрим частные случаи аффинного преобразования. 1. Параллельный сдвиг координат (рис. 2. 9). Рис. 2.9. Параллельный сдвиг координат В матричной форме Обратное преобразование: 2. Растяжение-сжатие осей координат (рис. 2. 10)
Обратное преобразование: Коэффициенты kx и ky могут быть отрицательными. Например, kx = -1 соответствует зеркальному отражению относительно оси y. 3. Поворот (рис. 2. 11). Рис.2.11. Поворот Обратное преобразование соответствует повороту системы (X, Y) на угол (-α). Свойства аффинного преобразования. • Любое аффинное преобразование может быть представлено как последовательность операций из числа указанных простейших: сдвиг, растяжение/сжатие и поворот. • Сохраняются прямизна линии, параллельность прямых, отношение длин отрезков, лежащих на одной прямой, и соотношение площадей фигур. Трехмерное аффинное преобразование Запишем в виде формулы: где А, В,..., Ν— константы. Дадим также запись в матричной форме:
Для трехмерного пространства любое аффинное преобразование также может быть представлено последовательностью простейших операций. Рассмотрим их. 1. Сдвиг осей координат соответственно на dx, dy, dz: 2. Растяжение/сжатие на кx, кy, кz. 3. Повороты. Можно сказать, что в трехмерном пространстве существует больше разновидностей поворота, сравнительно с двумерным пространством. Рассмотрим несколько частных случаев поворота. Поворот вокруг оси x на угол φ (рис. 2. 12). Рис. 2.12. Поворот вокруг оси X Поворот вокруг оси у на угол ψ (рис. 2. 13, сверху). Поворот вокруг оси z на угол γ (рис. 2. 13, снизу).
2.2 Проекции При использовании любых графических устройств обычно используют проекции. Проекция задает способ отображения объектов на графическом устройстве. Мы будем рассматривать только проекции на плоскость. Проецирование - отображение точек, заданных в системе координат с размерностью N, в точки в системе меньшей размерности. Проекторы (проецирующие лучи) - отрезки прямых, идущие из центра проекции через каждую точку объекта до пересечения с плоскостью проекции (картинной плоскостью). 2.2.1 Мировые и экранные координаты При отображении пространственных объектов на экране или на листе бумаги с помощью принтера необходимо знать координаты объектов. Мы рассмотрим две системы координат. Первая — мировые координаты, которые описывают истинное положение объектов в пространстве с заданной точностью. Вторая — система координат устройства отображения, в котором осуществляется вывод изображения объектов в заданной проекции. Назовем систему координат графического устройства экранными координатами (хотя это устройство и не обязательно должно быть подобно монитору компьютера). Пусть мировые координаты будут трехмерными прямоугольными координатами. Где должен размещаться центр координат, и какими будут единицы измерения вдоль каждой оси, для нас сейчас не очень важно. Важно то, что для отображения мы будем знать любые числовые значения координат отображаемых объектов. Для получения изображения в определенной проекции необходимо вычислить координаты проекции. Для синтеза изображения на плоскости экрана или бумаге используем двумерную систему координат. Основная задача — задать преобразования координат из мировых в экранные. 2.2.2 Основные типы проекций Изображение объектов на плоскости (экране дисплея) связано с геометрической операцией проектированием. В компьютерной графике используется несколько видов проектирования, но основных - два вида: параллельное и центральное. Проектирующий пучок лучей направляется через объект на картинную плоскость, на которую в дальнейшем находят координаты пересечения лучей (или прямых) с этой плоскостью. Рис. 2.14. Основные типы проекций При центральном проектировании все прямые исходят из одной точки.
При параллельном - считается, что центр лучей (прямых) бесконечно удален, а прямые параллельны. Каждый из этих основных классов разбивается еще на несколько подклассов в зависимости от взаимного расположения картинной плоскости и координатных осей.
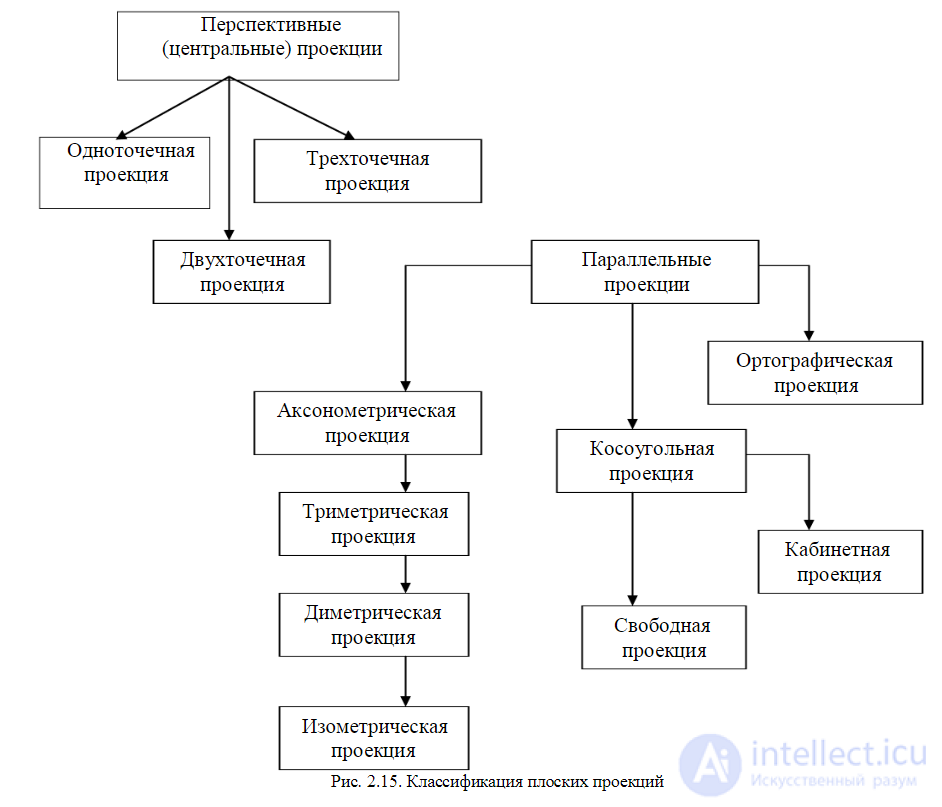
У параллельных проекций центр проекции расположен в бесконечности от плоскости проекции: ортографические (ортогональные), аксонометрические (прямоугольные аксонометрические) - проекторы перпендикулярны к плоскости проекции, расположенной под углом к главной оси, косоугольные (косоугольные аксонометрические) - плоскость проекции перпендикулярна к главной оси, проекторы расположены под углом к плоскости проекции. У центральных проекций центр проекции находится на конечном расстоянии от плоскости проекции. Имеют место так называемые перспективные искажения.
Ортогональные проекции (основные виды) Рис. 2.16. Ортогональные проекции 1. Вид спереди, главный вид, фронтальная проекция, (на заднюю грань V), 2. Вид сверху, план, горизонтальная проекция, (на нижнюю грань H), 3. Вид слева, профильная проекция, (на правую грань W), 4. Вид справа (на левую грань), 5. Вид снизу (на верхнюю грань), 6. Вид сзади (на переднюю грань). Матрица ортогональной проекции на плоскость YZ вдоль оси Х имеет вид: 1 0 0 00 1 0 00 0 1 00 0 0 0XP Если же плоскость параллельна, то эту матрицу надо умножить на матрицу сдвига, тогда: , 1 0 0 p0 1 0 00 0 1 00 0 0 0XP где р - сдвиг по оси Х; Для плоскости ZX вдоль оси Y , 1 0 q 00 1 0 00 0 0 00 0 0 0XP где q - сдвиг по оси Y; Для плоскости XY вдоль оси Z:
При аксонометрической проекции проектирующие прямые перпендикулярны плоскости картинки. Изометрия - все три угла между нормалью картинки и координатными осями равны. Диметрия - два угла между нормалью картинки и координатными осями равны. Триметрия - нормальный вектор плоскости картинки образует с координатными осями различные углы. Каждый из трех видов этих проекций получается комбинацией поворотов, за которой следует параллельное проектирование. При повороте на угол β относительно оси У (ординат), на угол α вокруг оси Х (абсцисс) и последующем проектировании оси Z (аппликат) возникает матрица Изометрическая проекция Рис. 2.17. Изометрические проекции Диметрическая проекция Рис. 2.18. Диметрические проекции
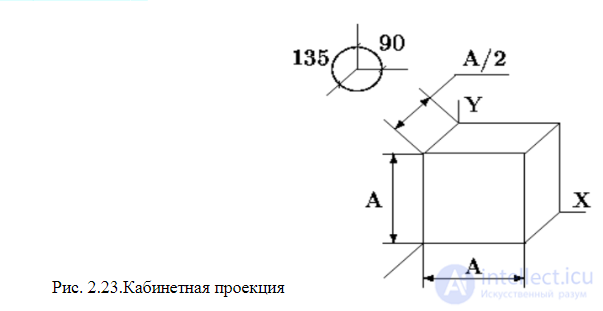
Косоугольные проекции Классический пример параллельной косоугольной проекции — кабинетная проекция (рис. 2. 26). Эта проекция часто используется в математической литературе для черчения объемных форм. Ось у изображается наклоненной под углом 45 градусов. Вдоль оси у масштаб 0. 5, вдоль других осей — масштаб 1. Запишем формулы вычисления координат плоскости проецирования Здесь, как и раньше, ось Υпр направлена вниз. Для косоугольных параллельных проекций лучи проецирования не перпендикулярны плоскости проецирования. Рис. 2.19. Косоугольные проекции Теперь относительно центральной проекции. Поскольку для нее лучи проецирования не параллельны, то будем считать нормальной такую центральную проекцию, главная ось которой перпендикулярна плоскости проецирования. Для центральной косоугольной проекции главная ось не перпендикулярна плоскости проецирования. Рассмотрим пример центральной косоугольной проекции, которая показывает параллельными линиями все вертикальные линии изображаемых объектов. Расположим плоскость проецирования вертикально, ракурс показа зададим углами а, β и положением точки схода (рис. 2. 21). Рис. 2.21. Вертикальная центральная косоугольная проекция: а – расположение плоскости проецирования, б – вид с левого торца плокости проецирования Будем считать, что ось Ζ видовых координат располагается перпендикулярно плоскости проецирования. Центр видовых координат — в точке (хс, ус, zc). Запишем соответствующее видовое преобразование:
Как и для нормальной центральной проекции, точка схода лучей проецирования располагается на оси Ζ на расстоянии Ζk от центра видовых координат. Необходимо учесть наклон главной оси косоугольной проекции. Для этого достаточно отнять от Υпр длину отрезка 0-0' (рис. 2.21). Эта длина равняется (Ζk - Ζпл) ctgβ. Теперь запишем результат — формулы вычисления координат косоугольной вертикальной проекции где Пх и Пу — это функции проецирования для нормальной проекции. Следует отметить, что для такой проекции нельзя сделать вид сверху (β = 0), поскольку здесь сtgP = ∞. Свойство рассмотренной вертикальной косоугольной проекции, заключающееся в сохранении параллельности вертикальных линий, иногда полезно, например, при изображении домов в архитектурных компьютерных системах. Сравните рис. 2. 22 (верх) и рис. 2.22 (низ). На нижнем рисунке вертикали изображаются вертикалями — дома не "разваливаются".

Кабинетная проекция (аксонометрическая косоугольная фронтальная диметрическая проекция)
Свободная проекция (аксонометрическая косоугольная горизонтальная изометрическая проекция) Рис. 2.24.Свободная проекция Центральная проекция Центральные проекции параллельных прямых, не параллельных плоскости проекции, сходятся в точке схода. В зависимости от числа координатных осей, которые пересекает плоскость проекции, различаются одно, двух и трехточечные центральные проекции. Рис. 2.25. Центральная проекция
Рассмотрим пример перспективной (центрально) проекции для вертикального расположения камеры, когда α = β = 0. Такую проекцию можно себе представить как изображение на стекле, через которое смотрит наблюдатель, расположенный сверху в точке (х, у, z) = (0, 0, zk). Здесь плоскость проецирования параллельна плоскости (х 0 у), как показано на рис. 2. 26. Для произвольной точки пространства (Р), исходя из подобия треугольников, запишем такие пропорции: Xпр/(zk – zпл) = x/(zk – z) Yпр /(zk – zпл) = y/(zk – z) Найдем координаты проекции, учитывая также координату Ζпр: Запишем такие преобразования координат в функциональном виде где Π — функция перспективного преобразования координат. Рис. 2.26.Перпективная проекция В матричной форме преобразования координат можно записать так:
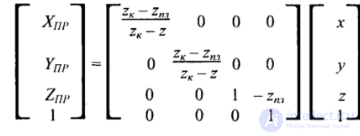
Обратите внимание на то, что здесь коэффициенты матрицы зависят от координаты z (в знаменателе дроби). Это означает, что преобразование координат — нелинейное (а точнее, дробно-линейное), оно относится к классу проективных преобразований. Мы получили формулы вычисления координат проекции для случая, когда точка схода лучей находится на оси z. Теперь рассмотрим общий случай. Введем видовую систему координат {X, Υ, Ζ), произвольно расположенную в трехмерном пространстве (х, у, z). Пусть точка схода находится на оси Ζ видовой системы координат, а направление обзора — вдоль оси Ζ противоположно ее направлению. Будем считать, что преобразование в видовые координаты описывается трехмерным аффинным преобразованием После вычисления координат (X, Y, Z) можно вычислить координаты в плоскости проецирования в соответствии с формулами, уже рассмотренными нами ранее. Поскольку точка схода находится на оси Ζ видовых координат, то Последовательность преобразования координат можно описать так: Такое преобразование координат позволяет моделировать расположения камеры в любой точке пространства и отображать в центре плоскости проецирования любые объекты обзора. Рис. 2.27. Центральная проекция точки P0 в плоскость Z = d
Исследование, описанное в статье про аффинные преобразования, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое аффинные преобразования, маштабирование, поворот и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Компьютерная графика
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Компьютерная графика
Термины: Компьютерная графика