Вопросы и ответы для самопроверки по теме позиционные задачи

Привет, мой друг, тебе интересно узнать все про пересечение плоскостей, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое пересечение плоскостей, пересечение поверхности с поверхностью, пересечение линии с линией, позиционные задачи , настоятельно рекомендую прочитать все из категории Начертательная геометрия и инженерная графика.

1. Какие задачи называются позиционными?

Позиционными называют задачи, связанные с решением вопросов взаимного расположения геометрических объектов относительно друг друга. В целом принято выделять две группы задач: Первая группа – задачи на взаимную принадлежность, они могут иметь следующие условия:

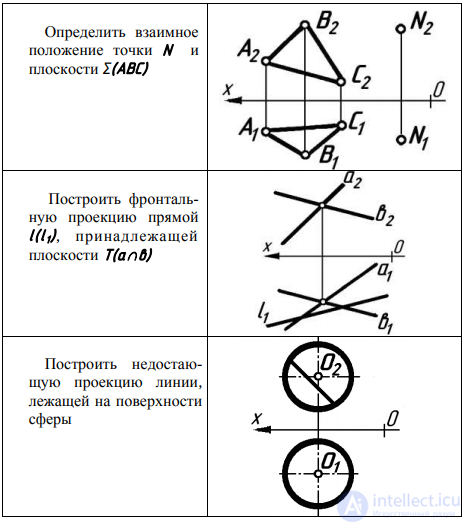
Вторая группа – задачи на взаимное пересечение, например:

2. Какова последовательность решения задач на пересечение на комплексном чертеже?

• пересечение линии с линией (l ∩ m)

  Решение задач на определение общей точки, принадлежащей как линии l, так и линии m, или иначе, задач по опредачению точки пересечения двух линий, вытекает непосредственно из инварианта ортогонального проецирования

• пересечение поверхности с поверхностью (α ∩ β)

  Две поверхности пересекаются по линии, точки которой принадлежат каждой из пересекающихся поверхностей.

• пересечение плоскостей

  Использование универсального алгоритма для решения задач по определению линии пересечения поверхностей проследим вначале на наиболее простых примерах пересечения двух плоскостей.

• Пересечение поверхности плоскостью (построение сечения)

  При пересечении поверхности или какой-либо геометрической фигуры плоскостью получается плоская фигура, которую называют сечением.

Пересечение линии с линией (l ∩ m)

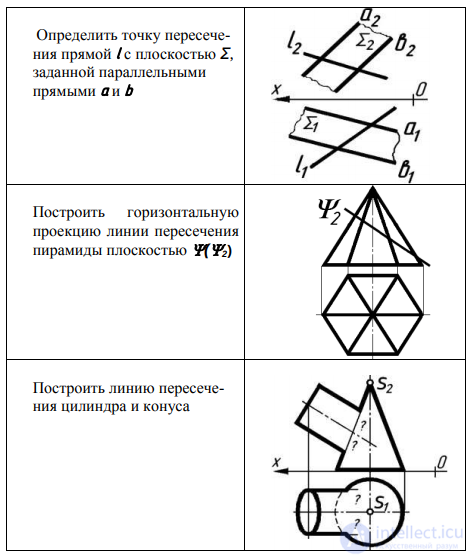
Решение задач на определение общей точки, принадлежащей как линии l, так и линии m, или иначе, задач по опредачению точки пересечения двух линий, вытекает непосредственно из инварианта ортогонального проецирования

K = a ∩ b ⇐⇒ K' = a' ∩ b' ∧ K" = a" ∩ b".

ПРИМЕР 1. Показать на эпюре Монжа две произвольные пересекающиеся линии m и n (рис. 180).

РЕШЕНИЕ. Пусть К = m ∩ n, тогда К ∈ m и К ∈ n. Из условия принадлежности К ∈ m вытекает К' ∈ m' и К" ∈ m". Так как К ∈ n, то К' ∈ n' и К" ∈ n". Для того чтобы m ∩ n, необходимо, чтобы К' и К" принадлежали одному перпендикуляру к оси x. На рис. 180 показаны пересекающиеся кривые m и n.

ПРИМЕР 2. Данную кривую l пересечь горизонталью h, проходящей через точку А (рис. 181).

РЕШЕНИЕ. Через A" проводим фронтальную проекцию горизонтали h" || оси х. Отмечаем точку К" = h" ∩ l". Находим К' ∈ l'. Точки К' и A' определяют горизонтальную проекцию h' горизонтали h.

Пересечение поверхности с поверхностью (α ∩ β)

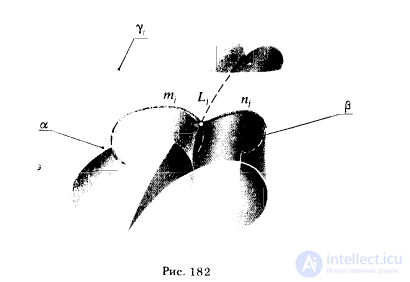
Две поверхности пересекаются по линии, точки которой принадлежат каждой из пересекающихся поверхностей. Поэтому построение линии пересечения двух поверхностей α и β сводится к нахождению общих точек, принадлежащих как множеству точек, составляющему поверхность α, так и другому множеству точек, входящих в состав поверхности β.

Способ построения линии пересечения двух поверхностей состоит в следующем: заданные поверхности пересекают третьей, вспомогательной поверхностью (вид и расположение вспомогательной секущей поверхности выбират с таким расчетом, чтобы можно было лег ко определить линии пересечения этой поверхности с заданными); находят линии, по которым эта вспомогательная секущая поверхность пересекает каждую из данных поверхностей. Далее отмечают точку (точки), в которой пересекаются полученные линии пересечения (рис. 182) .

Построив отмеченные операции n раз, получим множество точек. Линия l, соединяющая эти точки, является искомой линией пересечения поверхностей.

Используя геометрический язык, ход решения задачи можно представить в виде формализованного алгоритма, записанного в символической форме.

В табл. 8 дано традиционное для начертательной геометрии словесное описание алгоритма (слева) и соответствующая ему символическая запись на геометрическом языке (справа).

Таблица 8. Описание алгоритма решения задачи по определению линии пересечения двух поверхностей

Алгоритм нахождения точек, общих для двух заданных множеств точек - поверхностей α и β можно записать в виде

l = (L1 ∪ L2 ∪ L3 ∪ ... ∪ Ln); [Lj = (γj ∩ α) ∩ (γj ∩ β)]. (4)

Повторяя многократно последовательность операций, обозначенных в приведенном алгоритме (каждый раз, естественно, меняя положение вспомогательной секущей поверхности γj), можно получить любое число точек, принадлежащих искомой линии пересечения заданных поверхностей.

Рассматриваемый алгоритм определения точек, принадлежащих линии пересечения двух поверхностей, является универсальным, так как

под α и β могут подразумеваться любые поверхности, в том числе и плоскости. На выбор вида и расположения вспомогательной секущей поверхности γj в приведенном алгоритме также не накладывается никаких ограничений.

Вдумчивый читатель может задать вполне справедливый вопрос: "Что это за алгоритм, который предписывает решать задачи по определению точки (точек), принадлежащей линии пересечения двух поверхностей, путем решения двух задач, в каждой из которых также приходится строить линию пересечения поверхностей?".

Такое, на первый взгляд, нелогичное построение алгоритма становится вполне оправданным, если учесть, что данные поверхности α и β могут иметь любую форму и занимать произвольное положение в пространстве, что не позволяет непосредственно, по эпюру, определить линию их пересечения. А в качестве вспомогательной секущей поверхности γj мы можем выбрать поверхность удобной формы и так ориентировать ее относительно плоскостей проекций, чтобы получить простое решение для определения линии ее пересечения с каждой из заданных поверхностей.

Среди инвариантных свойств ортогонального проецирования находим (Ф ⊂ γ) ∧ (γ ⊥ π₁ ) ⇒ Ф' ⊂ h_0γ, т. е., если фигура Ф принадлежит поверхности γ ⊥ плоскости π₁ , то ортогональная проекция Ф' на эту плоскость принадлежит следу поверхности h_0γ (см. Об этом говорит сайт https://intellect.icu . § 6, свойство 2 г). Поэтому, если принять за вспомогательную секущую поверхность γ ⊥ π₁ (или π₂ ), то линии m_j и n_j пересечения этой поверхности с поверхностями α и β будут иметь горизонтальные (или фронтальные) проекции m'_j ⊂ h_0γj и n'_j ⊂ h_0γj (m"_j ⊂ f_0γj и n"_j ⊂ f_0γj ) т. е. решение подчас сложной задачи на построение линии пересечения поверхностей α и β мы заменяем решением двух простейших задач:

1) определить линию пересечения проецирующей поверхности γj с поверхностью α;

2) определить линию пересечения той же поверхности γj с поверхностью β.

Очевидно, что каждая из этих задач сводится к построению второй проекции линии, принадлежащей поверхности, если известна одна из ее проекций. Решение последней задачи состоит из многократного определения недостающей проекции точки, принадлежащей поверхности, т. е. сводится к решению позиционной задачи второго вида А ∈ α (см. § 40).

Пересечение плоскостей

Использование универсального алгоритма для решения задач по определению линии пересечения поверхностей проследим вначале на наиболее простых примерах пересечения двух плоскостей.

Две плоскости пересекаются по прямой линии, для определения которой достаточно найти две точки, принадлежащие одновременно каждой из заданных плоскостей.

Чтобы найти такие точки, достаточно ввести две вспомогательные секущие плоскости γ₁ и γ₂ т. е. дважды выполнить последовательность операций, предусмотренных частью алгоритма (4), заключенной в квадратные скобки (см. § 43):

L₁ = (γ₁ ∩ α) ∩ (γ₁ ∩ β);

L₂ = (γ₂ ∩ α) ∩ (γ₂ ∩ β);

l = (L₁, L₂).

Рассмотрим общий случай пересечения плоскостей, когда обе плоскости - общего положения.

ПРИМЕР 1. Определить линию пересечения l плоскостей α(a ∩ b) и β(c || d) (рис. 183).

РЕШЕНИЕ. Проводим вспомогательную горизонтально проецирующую плоскость γ₁(h_0γ1). Определяем проекции прямых m₁ = γ₁ ∩ α и n₁ = γ₁ ∩ β. Так как плоскость γ₁ | π₁ , то m'₁ и n'₁ совпадут с h_0γ1. С помощью точек 1', 2' и 3' 4' , принадлежащих прямым m'₁ и n'₁ определяем фронтальные проекции этих точек 1" , 2" и 3" , 4", которые определя прямые m"₁ и n"₁. Отмечаем точку пересечения фронтальных проекций прямых L"₁ = m"₁ ∩ n"₁. Горизонтальная проекция L'₁ принадлежит горизонтальным проекциям m'₁ и n'₁ .

Для нахождения точки L₂ вводим плоскость γ₂ || γ₁ . Плоскость γ₂ пересечет заданные плоскости по прямым m₂ и n₂, соответственно параллельным прямым m₁ и n₁ . Поэтому для определения их проекций достаточно найти проекции только одной точки, принадлежащей каждой из прямых m₂ и n₂ . На рис. 183

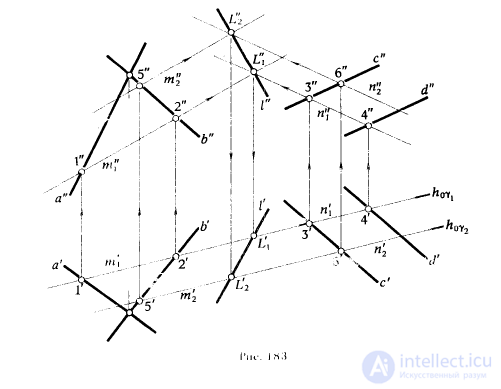
за такие точки приняты 5 и 6. Пересечение m₂ ∩ n₂ = L₂ . Точки L₁ и L₂ определяют искомую прямую l.

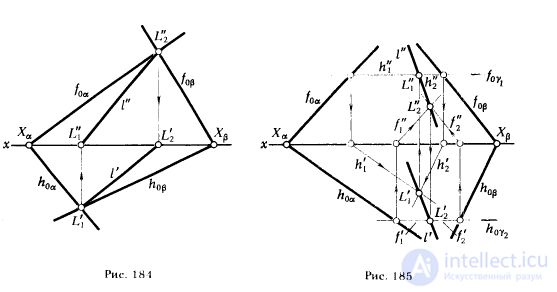
ПРИМЕР 2. Определить линию пересечения плоскостей α и β, заданных следами (рис. 184).

РЕШЕНИЕ. В данном случае решение значительно упрощается в связи с тем, что отпадает необходимость в выполнении построений, предусмотренных первым и вторым пунктами алгоритма (см.§ 43, табл. 8) . Это происходит потому, что роль вспомогательных секущих плоскостей γ₁ и γ₂ при задании плоскости следами могут выполнять плоскости проекций π₁ и π₂, а соответствующие следы h_0α, h_0β и f_0α, f_0β несут функции проекции прямых m' , n' и m" , n" . Следовательно, точки пересечения одноименных следов плоскостей α и β определяют положение проекций точек L₁ и L₂ .

L'₁ = h_0α ∩ h_0β и L"₂ = f_0α ∩ f_0β.-

Через одноименные проекции точек L₁ и L₂ проводим проекции искомой прямой l' и l".

Если одноименные следы плоскостей не пересекаются в пределах чертежа, то не представляется возможным использовать плоскости проекций в качестве вспомогательных секущих плоскостей. В этих случаях приходится вводить секущие плоскости, которые целесообразно проводить параллельно плоскостям проекций. Поясним сказанное на примере решения задачи по определению линии пересечения плоскостей α и β.

ПРИМЕР 3. Определить линию пересечения плоскостей α и β (рис. 185).

РЕШЕНИЕ. Вводим вспомогательные секущие плоскости γ₁ || π₁, и γ₂ || π₂. Эти плоскости пересекают заданные α и β по горизонталям h₁ и h₂ (плоскость γ₁ ) и фронталям f₁ и f₂ (плоскость γ₂ ) .

Находим точки L₁ и L₂: L'₁ = h'₁ ∩ h"₂; L"₂ = f"₁ ∩ f"₂. Зная L'₁ и L"₂, определяем L"₁ и L'₂. Через одноименные проекции точек L'₁L'₂ и L"₁L"₂ проводим проекции l' и l" искомой прямой пересечения плоскостей α и β.

Эту же задачу можно решить иначе. Вместо двух вспомогательных секущих плоскостей уровня взять одну плоскость γ общего положения, параллельную одной из заданных плоскостей α (или β) . Такой вариант решения основан на том что линии пересечения плоскости α двумя параллельными плоскостями β и γ параллельны между собой.

ПРИМЕР 4. Определить линию пересечения плоскостей α и β (рис. 186) .

РЕШЕНИЕ. Проводим вспомогательную секущую плоскость γ || β (h_0γ || h_0β и f_0γ || f_0β). Точку Х_γ выбираем так, чтобы одноименные следы плоскостей α и γ пересекались в пределах чертежа. Находим l₁ - линию пересечения плоскостей α и γ. Проекции l'₁ и l"₁ указывают направления проекций линии l пересечения плоскостей α и β.

Для определения точек, через которые пройдут эти проекции, рассмотрим ΔX_αL"₄X_γ ∼ ΔX_αL"₂X_β В ΔX_αL"₄X_γ (L"₄A"₃) || (L"₂L"₁) ΔX_αL"₂X_β, поэтому

Из этой пропорции определяем |Х_αL"₁| и через точку L"₁ проводим l" || l"₁.

Для нахождения горизонтальной про екции l' достаточно составить пропорцию:

Три отрезка из четырех заданы на чертеже, это дает возможность определить четвертый [Х_αL'₂]. Через точку L'₂ проводим l'|| l'₁ .

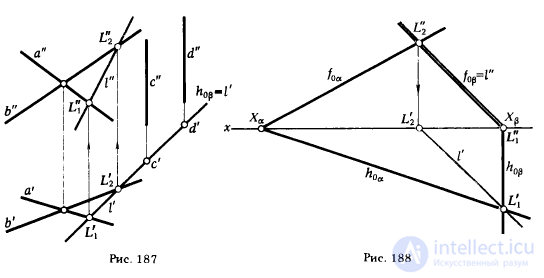
Решение задачи по определению линии пересечения плоскостей значительно упрощается, если одна из плоскостей занимает проецирующее положение. Из рис. 187 и 188 видно, насколько проще решается задача, когда одна из пересекающихся плоскостей - проецирующая, по сравнению с задачей (см. пример 1, рис. 183), в которой обе плоскости занимают общее положение. В этих случаях появляется возможность воспользоваться инвариантом (Ф ⊂ β)∧(β ⊥ π₁ ) ⇒ Ф' ⊂ h_0β, поэтому одна из проекций линии пересечения (l' на рис. 187 и l" на рис. 188) входит в состав исходных данных задачи (l' ≡ h_0β на рис. 187 и l" ≡ f_0β на рис. 188). Решение сводится к определению недостающей проекции прямой, принадлежащей плоскости (см. § 41, пример 2, рис. 179).

3. Какая прямая является линией пересечения плоскости общего положения с горизонтальной плоскостью уровня?

Рисунок 3.4 – Эпюры плоскостей частного положения

Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (Рисунок 3.4, г).

4. Какая прямая является линией пересечения плоскости общего положения с фронтально проецирующей плоскостью?

5. По какой линии пересекаются две фронтально проецирующие плоскости?

6. Как определяется видимость при пересечении двух плоскостей общего положения?

Определение видимости пересекающихся плоскостей на плоскостях проекций выполняем, используя Конкурирующие точки:

7. Как строится линия пересечения поверхностей плоскостью?

8. Какие линии могут быть получены в сечении прямого кругового цилиндра, конуса, сферы?

9. Что такое линия среза?

Линиями среза называют линии пересечения поверхностей вращения плоскостями, параллельными их оси (рис. 2.23).

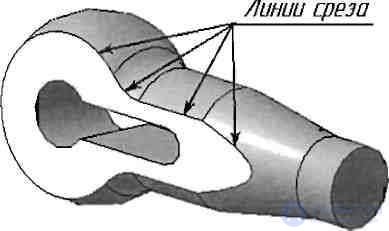
Рис. 2.23 - Образование линий среза

Эти линии на чертежах строят по точкам, как и все другие линии плоских сечений. На рис. 2.24 показано построение проекций линий среза на примере головки тяги. Ее поверхность сочетает сферу, тор, цилиндр и конус, попарно касающиеся по окружностям. Линии среза образованы в результате пересечения головки двумя фронтальными плоскостями аир, симметрично расположенными относительно оси ее поверхности. Эти плоскости пересекают сферу, тор, цилиндр и частично конус. Горизонтальные и профильные проекции линии среза совпадают со следами-проекциями (ан), (Ря)и(а^), (pV)соответственно.

Сфера пересекается плоскостями по окружности радиуса R, определяемого на горизонтальной (вид сверху) и профильной проекциях (вид слева). В точке 2" на фронтальной проекции дуга окружности переходит в линию среза тора, в точке 4" в линию среза цилиндра, в точке 5" в линию среза конуса. Фронтальную проекцию крайней правой точки линии среза конуса находят по горизонтальной проекции 71, получаемой от плоскости р. Для нахождения фронтальных проекций 2", З1, 4 , 5" и 6 промежуточных точек линии среза используют профильные плоскости Т, Р, S, Q, W и профильную проекцию головки. Построения показаны стрелками.

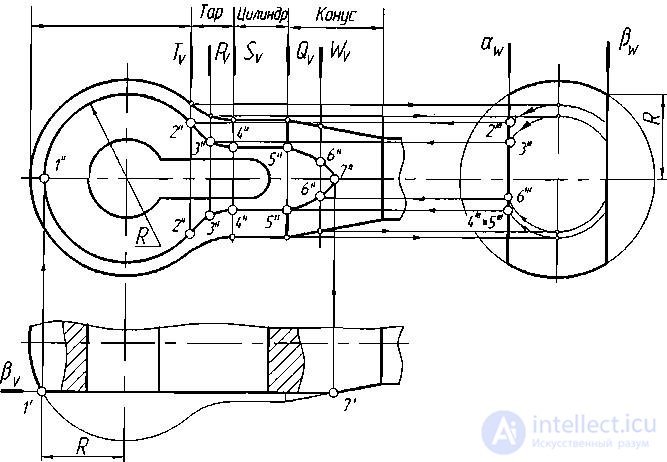
Рис. 2.24. – Построение проекций линий среза

10. Что представляет собой вырез?

На аксонометрическом изображении так же, как и на изображениях чертежа, применяют разрезы, с помощью которых показывают внутреннее устройство формы: плоскости, отверстия, углубления и т. п. Секущие плоскости, как правило, выбирают так, чтобы они совпадали с плоскостью симметрии детали (рис. 168, а) или отдельного ее элемента (рис. 168, б). На рисунке 168 показаны разрезы на аксонометрических проекциях, полученные с помощью фронтальной и профильной секущих плоскостей (рис. 168, а), фронтальной и горизонтальной плоскостей (рис. 168, б). Если секущая плоскость проходит вдоль тонкой стенки (ребра жесткости) детали, то на аксонометрическом изображении ее сечение заштриховывают (рис. 168). Линии штриховки сечений в аксонометрических проекциях наносят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях, стороны 'которых параллельны аксонометрическим осям (рис. 169). Существует несколько способов построения разрезов в аксонометрических проекциях. Первый из способов построения разрезов в аксонометрии заключается в том, что вначале по чертежу выполняют аксонометрическую проекцию детали (рис. 175, а). Затем наносят контуры сечений, образуемые каждой секущей плоскостью. После этого изображение передней части детали, находящейся между секущими плоскостями, удаляют и обводят оставшуюся часть изображения. Наносят штриховку. Рис. 168. Чертеж детали и ее аксономерическое изображение с вырезом (Секущая плоскость может совпадать с плоскостью симметрии всей детали (а) или ее элемента (б).) Рис. 169. Нанесение штриховки в изометрической проекции Рис. 170. Построение разреза в аксонометрии Второй способ построения разрезов в аксонометрии заключается в том, что сначала строят аксонометрическую проекцию фигуры сечений по размерам, взятым с чертежа, затем достраивают аксонометрическое изображение (оставшуюся часть детали) (рис. 170, б).

11. Чем можно задать необходимую форму выреза?

12. Как строят линию пересечения двух поверхностей?

13. Какие вспомогательные поверхности удобно использовать при построении точек линии пересечения двух поверхностей?

14. В чем сущность способа вспомогательных секущих плоскостей в построении линии пересечения двух поверхностей?

15. По каким линиям пересекаются соосные поверхности вращения?

16. Когда можно использовать вспомогательные сферы при построении линии пересечения двух поверхностей?

17. По каким линиям пересекаются два прямых круговых цилиндра одного диаметра, если их оси пересекаются? Почему?

18. Какую линию называют линией перехода и как она вычеркивается при изображении пересекающихся поверхностей?

Тебе нравиться пересечение плоскостей? или у тебя есть полезные советы и дополнения? Напиши другим читателям ниже. Надеюсь, что теперь ты понял что такое пересечение плоскостей, пересечение поверхности с поверхностью, пересечение линии с линией, позиционные задачи и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Начертательная геометрия и инженерная графика

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.