ВОПРОСЫ И ответы ДЛЯ САМОПРОВЕРКИ по начертательной геометрии кратко

Привет, мой друг, тебе интересно узнать все про ответы для самопроверки по начертательной геометрии, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое ответы для самопроверки по начертательной геометрии , настоятельно рекомендую прочитать все из категории 11. Метрические задачи.

1. Какие задачи называются метрическими?

2. Какие группы задач выделяются в метрических задачах?

Метрическими называются задачи, решение которых связано с нахождением характеристик геометрических фигур, определяемых (измеряемых) линейными и угловыми величинами.

Все многообразие метрических задач, в конечном счете, сводится к двум видам: А - задачам на определение расстояния между двумя точками; Б - задачам на нахождение величины угла между двумя пересекающимися прямыми.

К метрическим относятся также задачи на построение отрезка и угла с наперед заданным значением соответственно линейной и градусной (радианной) величины.

Несмотря на то, что чисто метрические задачи встречаются редко, целесообразно выделйть их в самостоятельную группу, включив в нее и те задачи, в которых на промежуточных этапах решения приходится выяснять позиционные отношения между геометрическими фигурами.

В основе алгоритма решения любой метрической задачи лежит инвариантное свойство ортогонального проецирования, заключающееся в том, что любая фигура, принадлежащая плоскости, параллельной плоскости проекции, проецируется на эту плоскость в конгруентную фигуру, т. е. (Ф ⊂ β) ∧ (β || π1) ⇒ Ф' ≅ Ф.

3. Как на комплексном чертеже определить расстояние между двумя точками пространства; от точки до прямой; от точки до плоскости?

Определение расстояния от точки до точки и от точки до прямой

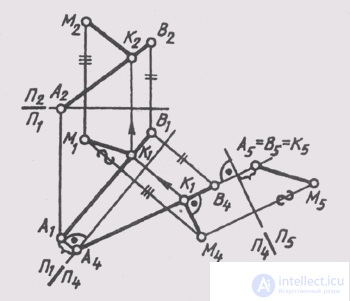
1) П2_|_П1-> П1_|_П4, П4 ||АВ, П1/П4 ||A1B1;

2) П1П4 -> П4_|_П5, П5 _|_AB, П4/П5 _|_A4B4;

3) M5K5 — истинное расстояние от точки М до прямой AB;

4) чтобы построить проекции перпендикуляра МК в исходной системе плоскостей, строят основание перпендикуляра— точку К—на прямой АВ из условия, что в системе П4 _|_П5; он занимает положение линии уровня, т. е.

M4K4_|_A4B4. Горизонтальная и фронтальная проекции точки К определяются по линиям из условия принадлежности ее прямой АВ. Расстояние от точки до плоскости измеряется отрезком перпендикуляра, опущенного из точки на плоскость. Так как перпендикуляр к проецирующей плоскости есть линия уровня, то удобно иметь на чертеже «вырожденную» проекцию данной плоскости, т. е. преобразовать чертеж

4. Как определить кратчайшее расстояние между двумя параллельными прямыми; скрещивающимися прямыми; от прямой до плоскости?

Задача решается способом двойной замены плоскостей проекций. На заключительном этапе одна из плоскостей проекций должна быть перпендикулярной к одной из скрещивающихся прямых. Тогда кратчайшее расстояние между ними определяется величиной отрезка перпендикуляра к другой скрещивающейся прямой (рис. 199).

Первая замена плоскостей проекций Пх/Т.2 на новую Ylx/Y4 преобразует прямую общего положения АВ в прямую уровня и отрезок А4В4 || П4. Последующая замена плоскостей проекций П]/П4на П4/П5 преобразует прямую уровня в проецирующую прямую, которая на П5 вырождается в точку А5 = В5. Искомая проекция M5N5 ота2

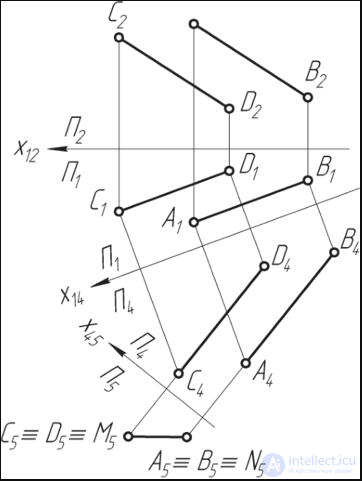
Рис. 199

резка MN перпендикулярна C5D5 и изображается в натуральную величину. С помощью проекционных линий связи производят построения отрезка MN на других плоскостях проекций. Об этом говорит сайт https://intellect.icu . Следует помнить, что проекция искомого отрезка M4N4 на плоскости П4 перпендикулярна линиям связи, так как отрезок MN в системе плоскостей проекций П4/П5 является прямой уровня и перпендикулярен к прямой АВ.

5. Какие построения необходимо выполнить на чертеже, чтобы определить натуральную величину угла между двумя пересекающимися прямыми общего положения?

6. Как по чертежу определить истинную величину угла между плоскостями общего положения, если ребро образованного ими двугранного угла не задано?

7. Какие вы знаете способы построения истинной величины фигуры сечения поверхности плоскостью общего положения?

8. Что называется разверткой поверхности?

Разверткой многогранной поверхности называется плоская фигура, получаемая последовательным совмещением всех граней поверхности с плоскостью.

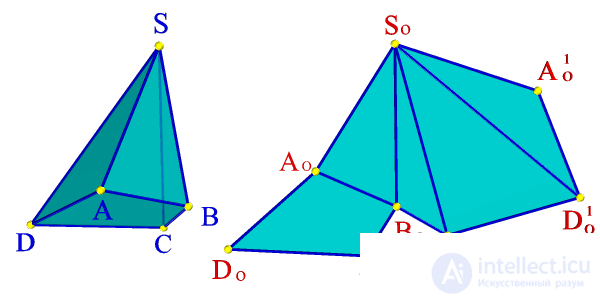
а) модель		б) эпюр
Рисунок 136. Пирамида и ее развертка

9. Какие поверхности относятся к неразвертывающимся поверхностям?

10. Можно ли построить развертку неразвертывающейся поверхности?

К развертывающимся поверхностям относятся все многогранные поверхности. Разверткой многогранной поверхности является плоская фигура, полученная последовательным совмещением с одной и той же плоскостью всех ее граней, поэтому построение развертки многогранной поверхности сводится к построению истинных размеров и формы отдельных граней, которые затем совмещают с плоскостью без изменения формы и размеров.

Из кривых поверхностей, к развертывающимся относятся линейчатые поверхности, которые образованы взаимно-параллельными или пересекающимся образующими. К таким поверхностям относятся торсы и их частные виды – конические и цилиндрические поверхности. Остальные линейчатые и нелинейчатые поверхности относятся к неразвертывающимся поверхностям.

Развертки развертывающихся и неразвертывающихся поверхностей, которые, как правило, строятся графически, являются приближенными. При построении этих разверток заданную поверхность заменяют (аппроксимируют) другой поверхностью, которую вписывают или описывают около нее. Аппроксимирующими поверхностями выбирают развертывающиеся поверхности. Линейчатые поверхности заменяют многогранными, например, цилиндр – вписанной в него призмой, конус –вписанной в него пирамидой, а торс – вписанной в него многранной поверхностью (гранный торс). Поверхности с криволинейными образующими предварительно заменяют цилиндрическими и коническими поверхностями вращения, которые затем заменяют многогранными. Количество граней в аппроксимирующей поверхности должно быть достаточным для обеспечения необходимой точности построения развертки.

11. Каким способом строят развертки пирамидальных (конических) поверхностей?

Построение разверток пирамидальных поверхностей сводится к многократному построению натурального вида треугольников, из которых состоит данная пирамидальная поверхность или многогранная поверхность. Так как этот способ приводит к разбивке поверхности на треугольники, то он называется способом треугольников (триангуляция.)

Построение разверток конических поверхностей, несмотря на то, что конические поверхности являются развертывающимися и, следовательно, имеют теоретически точные развертки, практически строят их приближенные развертки, пользуясь способом треугольников. Для этого заменяют коническую поверхность вписанной в нее поверхностью пирамиды.

Коническая поверхность имеет плоскость симметрии, поэтому можно построить развертку только одной половины поверхности.

Разделив от центра основания конуса на шесть равных частей и определив с помощью прямоугольных треугольников натуральные величины образующих, проведенных в точки деления, строим шесть примыкающих один к другому треугольников с общей вершиной S.

Каждый из этих треугольников строится по трем сторонам; при этом две стороны равны натуральной величине образующих, а третья-хорде, стягивающей дугу окружности основания между соседними точками деления. После этого по хордам основания конической поверхности проводится плавная кривая. Это приближенное построение развертки поверхностей вращения.

Для построения развертки конической поверхности с круговым основанием сводится к вписанию в нее двенадцатигранной пирамиды.

Для построения развертки цилиндрической проекции, заменяем данную поверхность вписанной в нее призматической поверхностью. Так как цилиндрическая поверхность так же как и коническая имеет плоскость симметрии, аналогичное решение применяется и в этом случае. Тогда поверхность половины цилиндра разобьется на шесть частей. Определив натуральную величину образующих, так же строится приближенная развертка цилиндрической поверхности.

12. Каким способом строят развертки призматических (цилиндрических) поверхностей?

Построение разверток призматических и цилиндрических поверхностей приводит в общем случае к многократному построению натурального вида трапеций, из которых состоит данная призматическая поверхность, или призматическая поверхность, вписанная (или описанная) в данную цилиндрическую поверхность и заменяющая ее. Если, в частности, призматическая или цилиндрическая поверхности ограниченны параллельными основаниями, то трапеции, на которые разбивается поверхность, обращаются в прямоугольники или параллелограммы, в зависимости от того, перпендикулярны или нет плоскости оснований боковым ребрам или образующим поверхности.

Построение разверток поверхностей имеет большое практическое значение при конструировании различных изделий из листового материала.

13. Как нанести на развертку поверхности точку, ей принадлежащую?

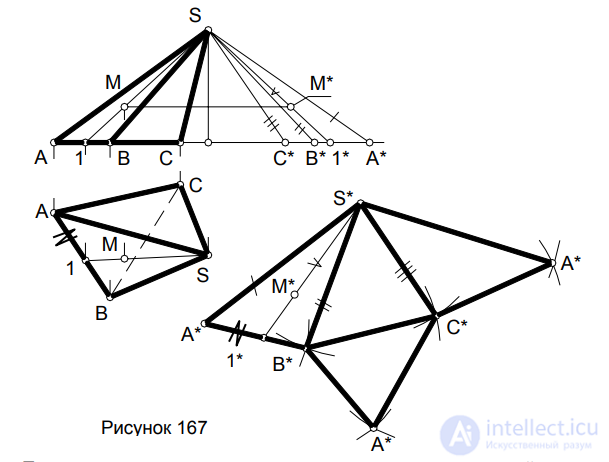
Пример 1. Построить полную развертку поверхности треугольной пирамиды SABC, нанести на развертку точку М, заданную своей фронтальной проекцией (рисунок 167).

Так как боковые грани пирамиды являются треугольниками, то необходимо построить натуральные виды этих треугольников. Для этого нужно предварительно определить натуральные величины боковых ребер пирамиды. Это можно сделать при помощи способа прямоугольных треугольников, в каждом из которых одним из катетов будет превышение вершины пирамиды S над точками А, В и С, а вторым катетом – отрезок, равный горизонтальной проекции соответствующего бокового ребра SA, SB или SC.

Поскольку основание пирамиды является горизонтальной плоскостью, то на виде сверху имеем его натуральную величину и величины его сторон можно измерить непосредственно на виде сверху (горизонтальной проекции). Треугольник каждой боковой грани строится по трем сторонам. Развертка боковой поверхности пирамиды получается в виде трех примыкающих друг к другу треугольников с общей вершиной S*. Теперь остается пристроить к развертке боковой поверхности треугольник А*В*С* (по трем сторонам, измеренным на виде сверху), являющийся натуральным видом основания пирамиды.

Для нанесения на развертку точки М, сначала достроим ее го ризонтальную проекцию. С этой целью «привяжем» точку М к по верхности пирамиды отрезком S1, на горизонтальной проекции которого и определится горизонтальная проекция точки М. Построим
на развертке указанный отрезок S1, для чего измерим расстояние от
точки А основания пирамиды до точки 1 на виде сверху (горизонтальной проекции). Отложив полученную величину на развертке,
получим положение точки 1* на отрезке А*В* боковой грани пирамиды. Чтобы найти точку М* на отрезке S*1*, предварительно опреде-
лим его натуральную величину тем же способом прямоугольноготреугольника. Расстояние от вершины S пирамиды до точки М находим переносом фронтальной проекции точки на натуральную ве-
личину S*1*. Отложив на развертке вдоль отрезка S*1* величину S*M*, находим положение точки М на развертке.
     После построения развертки боковой поверхности пирамиды следует пристроить к ней треугольник основания А*В*С*.

Тебе нравиться ответы для самопроверки по начертательной геометрии? или у тебя есть полезные советы и дополнения? Напиши другим читателям ниже. Надеюсь, что теперь ты понял что такое ответы для самопроверки по начертательной геометрии и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории 11. Метрические задачи

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.