Линейная перспектива кратко

Привет, мой друг, тебе интересно узнать все про линейная перспектива, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое линейная перспектива , настоятельно рекомендую прочитать все из категории Начертательная геометрия и инженерная графика.

КОМПОЗИЦИЯ ЧЕРТЕЖА

Компоненты композиции :

Положение главного луча

Расстояние точки зрения (угол зрения)

Положение горизонта

Положение главного луча зависит от композиции объекта:

а) при симметричной композиции луч рекомендуется проводить через середину объекта

б) при большем развитии одной из частей композиции луч смещается ближе к этой части

Расположение главного луча вне средней трети луча зрения

не допустимо

Перспектива прямых частного положения

АППАРАТ ПЕРСПЕКТИВЫ

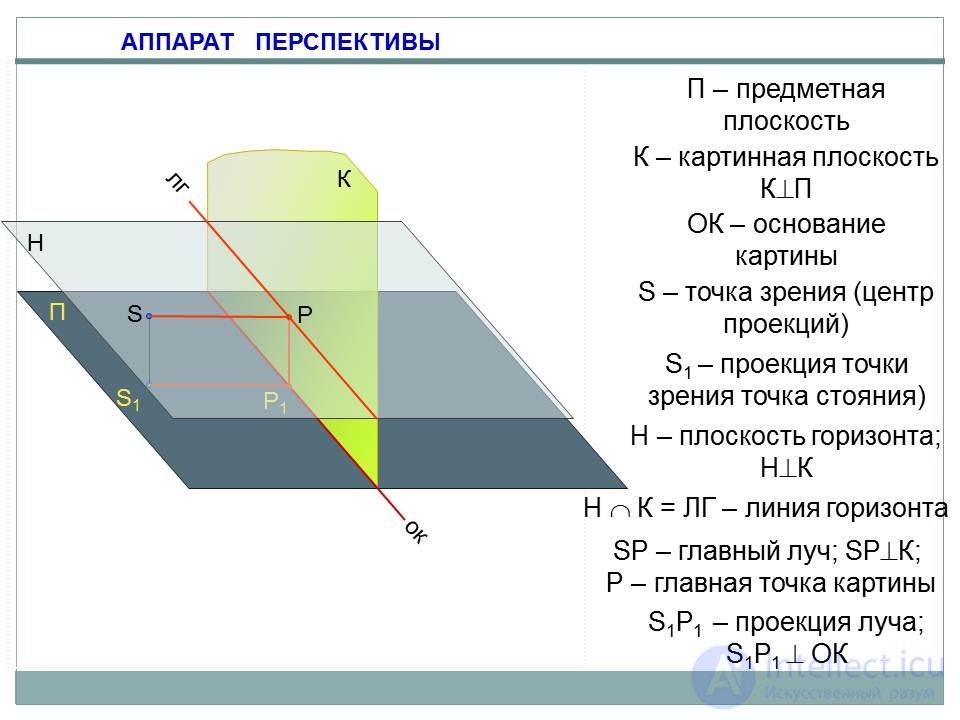
Перспектива горизонтальных прямых

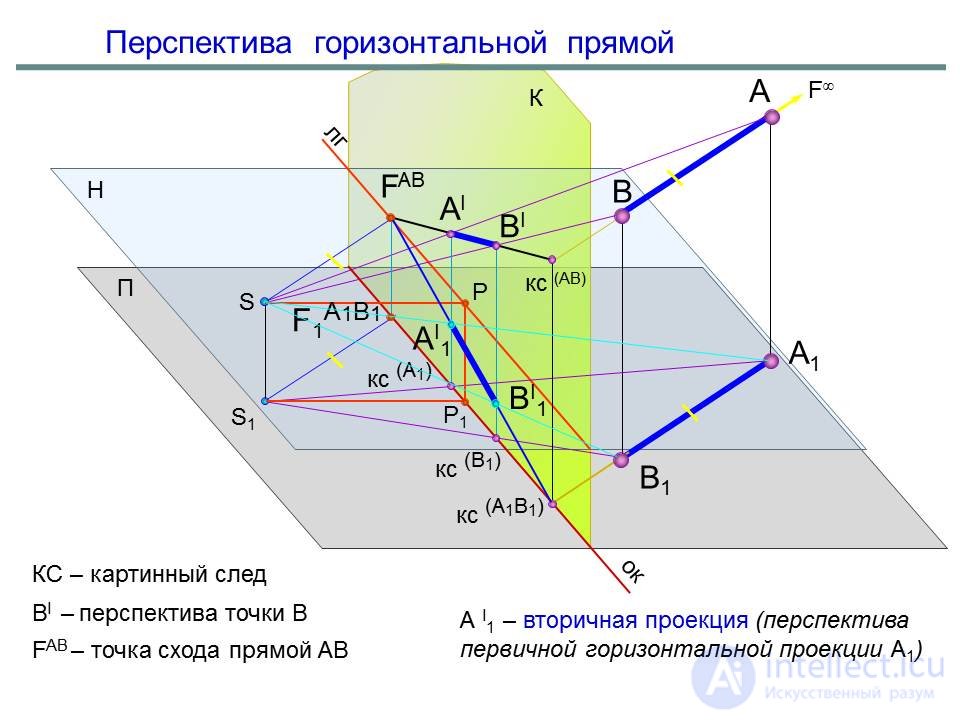
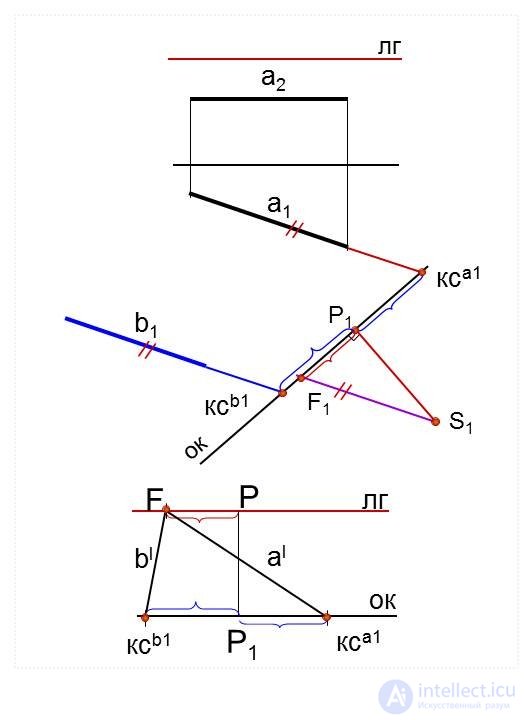
Горизонтальные прямые имеют точку схода на линии горизонта

Перспектива горизонтальных прямых строится по двум точкам:

1 – картинный след – точка пересечения прямой с картиной К;

2 – точка схода прямой – точка пересечения с картиной К луча из S, параллельного этой прямой

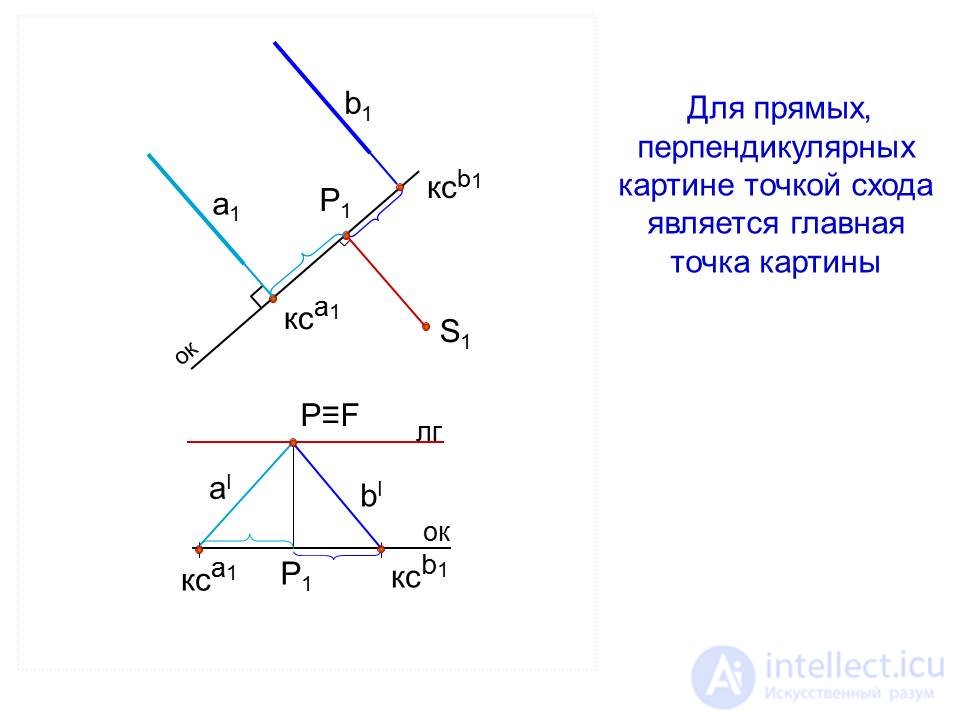
Перспектива прямой, перпендикулярной картине

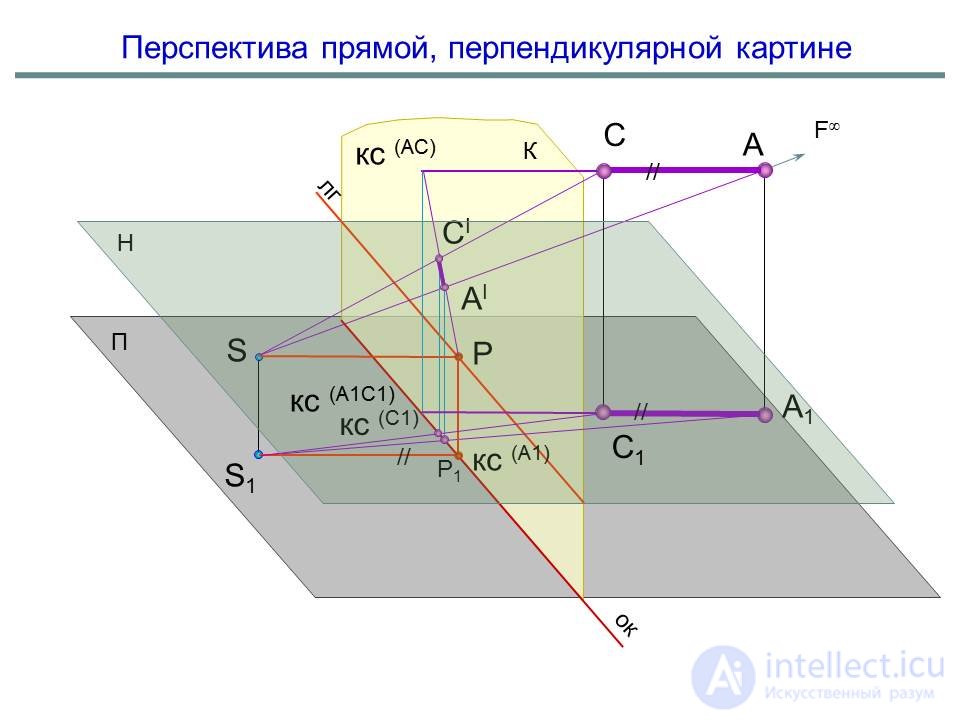
Для прямых, перпендикулярных картине точкой схода является главная точка картины

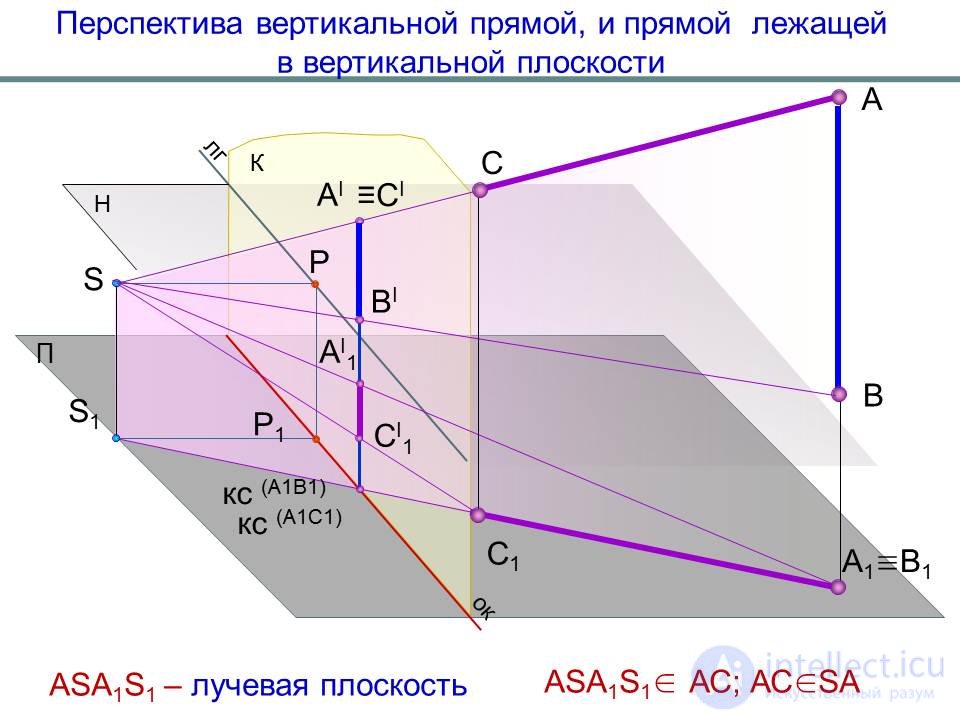
Перспектива вертикальной прямой, и прямой лежащей в вертикальной плоскости

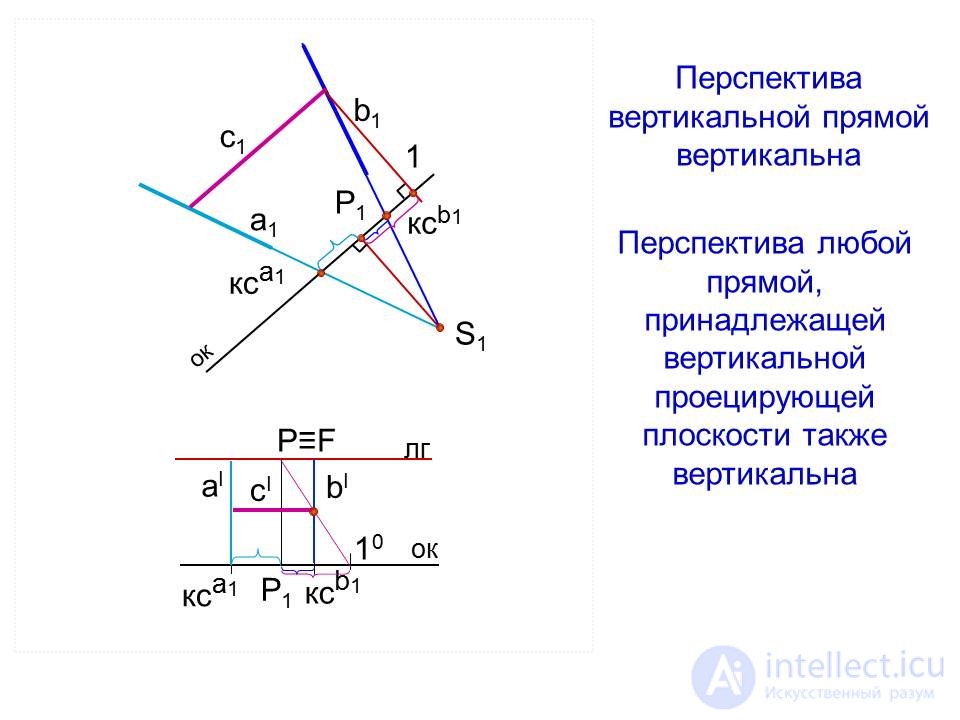
Перспектива вертикальной прямой вертикальна

Перспектива любой прямой, принадлежащей вертикальной проецирующей плоскости также вертикальна

Перспектива прямой общего положения

Пучок параллельных между собой прямых общего положения имеет общую точку схода прямых в перспективе

Точка схода прямых общего положения в перспективе не лежит на линии горизонта

Выбор угла зрения

ВЫБОР ТОЧКИ ЗРЕНИЯ

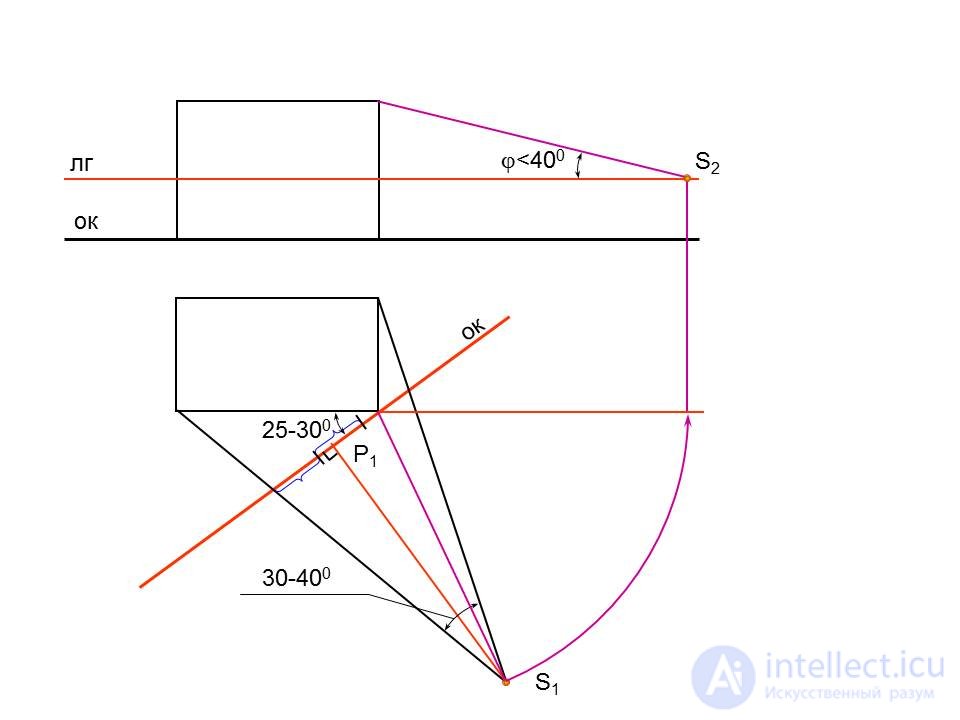
В начале пособия в определении понятия "перспектива" говорилось о необходимости соблюдать некоторые условия, ограничивающие взаимное положение точки зрения, картины и объекта. Эти ограничения зависят от особенностей нашего зрения и составляют понятие "выбор точки зрения". Правильный "выбор" имеет большое композиционно-художественное значение. Об этом говорит сайт https://intellect.icu . От него в высшей степени зависят эффективность, ясность и, главное, точность восприятия перспективного изображения.

Рис. 20 Рис. 21

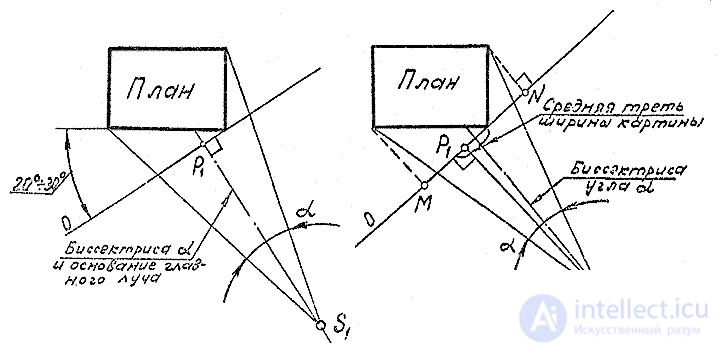В основе выбора точки зрения лежит правило: "относительное расположение изображаемого объекта, точки зрения и картинной плоскости должно быть таково, чтобы этот объект находился полностью внутри такого кругового конуса, у которого вершина совпадает с точкой зрения, ось перпендикулярна картинной плоскости и диаметр круга основания на картине укладывается в высоте конуса от одного до трех раз. При этом угол между образующиии конуса при вершине будет изменяться от 53° до 18°. При угле 28° диаметр круга основания укладывается в высоте два раза. На плоскость П₁ (рис. 20) угол проецируется в угол между прямыми, проведенными через основание S₁ точки зрения S и крайние точки плана изображаемого объекта; высота конуса проецируется а биссектрису этого угла. Как правило основание S₁P₁ главного луча SP совпадает с биссектрисой угла . Основание картины О располагается перпендикулярно биссектрисе.

Рис. 22

В некоторых случаях в зависимости от формы объекта допускается несовпадение биссектрисы угла и основания главного луча. Но, при этом, необходимо, чтоб точка P₁ находилось в средней трети ширины картиныMN (рис. 21). Основание картины должно быть перпендикулярно S₁P₁.. При выборе точки зрения S(S₁) помимо обеспечения наилучшего угла зрения (28°) необходимо показать на перспективе главный и боковой фасады здания или сооружения. Это возможно, если точки зрения S(S₁) располагаются так, как показано на рис. 20, 21, 23. При этом получается так называемая у г л о в а я перспектива. Оптимальный угол наклона картины к плоскости главного фасада находится в пределах 20 - 30°. Угловая перспектива используется для построения изображения отдельного здания или сооружения.
Если точка зрения располагается так, как показано на рис. 22, перспектива называется фронтальной и используется для построения изображений улиц, площадей.
Расстояние точки зрения до предметной плоскости SS₁ = 1,7м (перспектива с нормальной высотой горизонта).
Существуют: перспектива "с птичьего полета"- высота точки зрения до 100 м и более;
перспектива при виде снизу - точка зрения выбирается ниже предметной плоскости. На рис. 23 показаны перспективы одного объекта при четырех различных высотах горизонта (Н₁, Н₂, Н₃, Н₄) .
Практически положение точки S на плане выбирают следующим образом: 1. Вырезают на картонном листе просвет с углом 28° или берут прозрачный треугольник с углом 30°. Наложив его на лист, располагают так, чтобы стороны шаблона прошли через крайние точки плана, отмечают в вершине угла основание S₁ точки зрения S и проводят через точку S₁ и крайние точки плана прямые.
2. Через точку S₁ проводят биссектрису угла , которая одновременно будет основанием главного луча.
3. Через ближайший к точке зрения угол здания проводят основание картинной плоскости перпендикулярно биссектрисе угла и отмечают основание Р₁ главной точки Р(Р₁ = ОS₁P₁) . Если угол между картинной плоскостью и плоскостью главного фасада будет выходить за пределы 20-30°, следует повторить построение, изменив положение точки S₁.

Рис. 24

Еще одно замечание относительно выбора положения картинной плоскости.
Картине может занимать три положения:
а) находиться между зрителем и объектом;
б) пересекать объект;
в) находиться позади объекта.
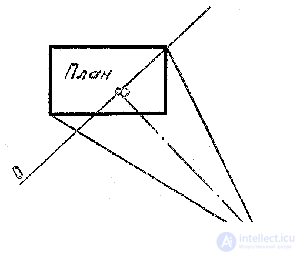
Первое положение самое употребительное, но перспективное изображение, при этом, получается уменьшенных размеров, поэтому в учебной работе рекомендуется картинной плоскостью пересекать объект (на предметной плоскости основание картины О пересекает план здания) (рис. 24).

Рис. 23

СПОСОБЫ ПОСТРОЕНИЯ ПЕРСПЕКТИВЫ ГЕОМЕТРИЧЕСКИХ ОБЪЕКТОВ

1. Способ архитекторов. В основу этого способа положено свойство перспективных проекций параллельных прямых, которое заключается в том, что они сходятся в одной точке (имеют общую точку схода F).

2. Радиальный способ заключается в том, что перспектива любой точки определяется как след луча зрения (т.е. как точка пересечения луча зрения, проходящего через заданную точку, с картинной плоскостью). Способ разработан немецким художником, математиком и гравером Альбертом Дюрером (1471 − 1528) и поэтому иногда называется способом Дюрера.

3. Способ сетки. Способ построения перспективы с помощью сетки заключается в том, что предварительно на ортогональных проекциях наносят равномерную ортогональную сетку, а затем строят перспективное изображение этой сетки.

Тебе нравиться линейная перспектива? или у тебя есть полезные советы и дополнения? Напиши другим читателям ниже. Надеюсь, что теперь ты понял что такое линейная перспектива и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Начертательная геометрия и инженерная графика

Из статьи мы узнали кратко, но содержательно про линейная перспектива