22. Лекальные кривые на чертежах кратко

Привет, мой друг, тебе интересно узнать все про лекальные кривые, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое лекальные кривые , настоятельно рекомендую прочитать все из категории Начертательная геометрия и инженерная графика.

Лекальными называют плоские кривые, вычерченные с помощью лекал по предварительно построенным точкам. К лекальным кривым относят: эллипс параболу, гиперболу, циклоиду, синусоиду эвольвенту и др.

Эллипс представляет собой замкнутую плоскую кривую второго порядка. Она характеризуется тем, что сумма расстояний от любой ее

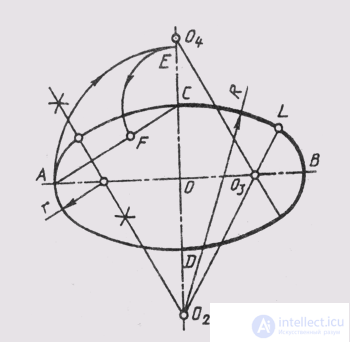
Рис. 36

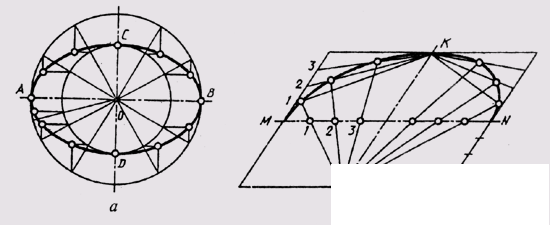
Рис. 37

точки до двух точек фокусов есть величина постоянная, равная большей оси эллипса. Построить эллипс можно несколькими способами. Например, можно построить эллипс по его большой АВ и малой CD осям (рис. 37, а). На осях эллипса как на диаметрах строят две окружности, которые можно разделить радиусами на несколько частей. Через точки деления большой окружности проводят прямые, параллельные малой оси эллипса, а через точки деления малой окружности — прямые, параллельные большой оси эллипса. Точки пересечения этих прямых и являются точками эллипса.

Можно привести пример построения эллипса по двум сопряженным диаметрам (рис. 37,б) MN и KL. Сопряженными два диаметра называют, если каждый из них делит пополам хорды, параллельные другому диаметру. На сопряженных диаметрах строят параллелограмм. Один из диаметров MN делят на равные части; на такие же части делят и стороны параллелограмма, параллельные другому диаметру, нумеруя их, как показано на чертеже. Из концов второго сопряженного диаметра KL через точки деления проводят лучи. Об этом говорит сайт https://intellect.icu . В пересечении одноименных лучей получают точки эллипса.

Параболой называют незамкнутую кривую второго порядка, все точки которой равно удалены от одной точки — фокуса и от данной прямой — директрисы.

Рассмотрим пример построения параболы по ее вершине О и какой-либо точке В (рис. 38, а). С этой целью строят прямоугольник ОABC и делят его стороны на равные части, из точек деления проводят лучи. В пересечении одноименных лучей получают точки параболы.

Можно привести пример построения параболы в виде кривой, касательной прямой с заданными на них точками А и В (рис. 38, б). Стороны угла, образованного этими прямыми, делят на равные части и ну-

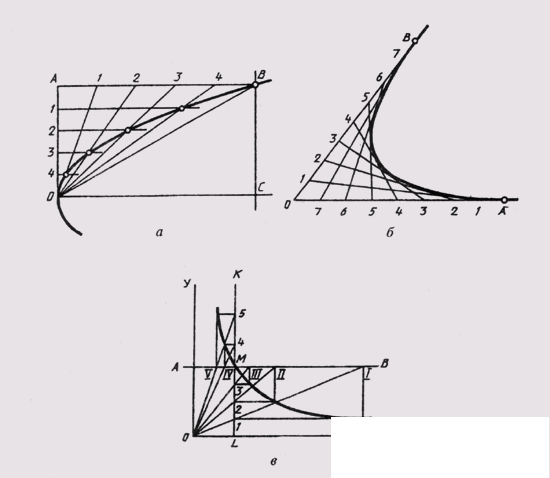
Рис. 38

меруют точки деления. Одноименные точки соединяют прямыми. Параболу вычерчивают как огибающую этих прямых.

Гиперболой называют плоскую незамкнутую кривую второго порядка, состоящую из двух веток, концы которых удаляются в бесконечность, стремясь к своим асимптотам. Гипербола отличается тем, что каждая точка ее обладает особым свойством: разность ее расстояний от двух данных точек-фокусов есть величина постоянная, равная расстоянию между вершинами кривой. Если асимптоты гиперболы взаимно перпендикулярны, она называется равнобокой. Равнобокая гипербола широко применяется для построения различных диаграмм, когда задана своими координатами одна точка М (рис. 38, в). В этом случае через заданную точку проводят линии АВ и KL параллельно координатным осям. Из полученных точек пересечения проводят линии, параллельные координатным осям. В их пересечении получают точки гиперболы.

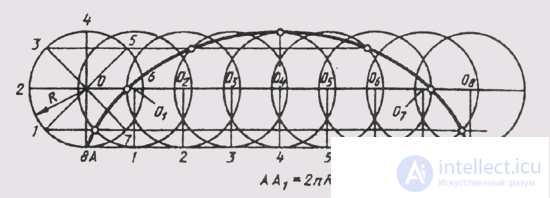
Рис. 39

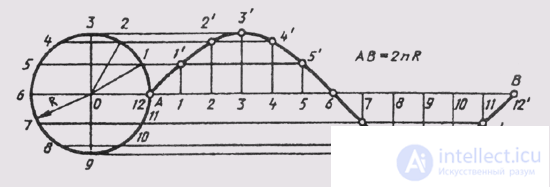
Рис. 40

Циклоидой называют кривую линию, представляющую собой траекторию точки А при перекатывании окружности (рис. 39). Для построения циклоиды от исходного положения точки А откладывают отрезок АА], отмечают промежуточное положение точки А. Так, в пересечении прямой, проходящей через точку 1, с окружностью, описанной из центра О₁, получают первую точку циклоиды. Соединяя плавной прямой построенные точки, получают циклоиду.

Синусоидой называют плоскую кривую, изображающую изменение синуса в зависимости от изменения его угла. Для построения синусоиды (рис. 40) нужно разделить окружность на равные части и на такое же количество равных частей разделить отрезок прямой АВ = 2лR. Из одноименных точек деления провести взаимно перпендикулярные линии, в пересечении которых получают точки, принадлежащие синусоиде.

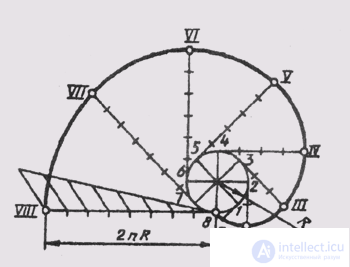
Рис. 41

Эвольвентой называют плоскую кривую, являющуюся траекторией любой точки прямой линии, перекатываемой по окружности без скольжения. Построение эвольвенты выполняют в следующем порядке (рис. 41): окружность делят на равные части; проводят касательные к окружности, направленные в одну сторону и проходящие через каждую точку деления; на касательной, проведенной через последнюю точку деления окружности, откладывают отрезок, равный длине окружности 2лR, который делят на столько же равных частей. На первой касательной откладывают одно деление 2лR/n , на второй — два и т. д.

Полученные точки соединяют плавной кривой и получают эвольвенту окружности.

Тебе нравиться лекальные кривые? или у тебя есть полезные советы и дополнения? Напиши другим читателям ниже. Надеюсь, что теперь ты понял что такое лекальные кривые и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Начертательная геометрия и инженерная графика