ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ По начертательной геометрии с ответами

Привет, мой друг, тебе интересно узнать все про вопросы для самопроверки по начертательной геометрии с ответами, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое вопросы для самопроверки по начертательной геометрии с ответами , настоятельно рекомендую прочитать все из категории Начертательная геометрия и инженерная графика.

1. Как разделить отрезок пополам?

найдем середину отрезка, концы которого А и В заданы, с помощью одного циркуля - не проводя самого отрезка. Вот решение этой задачи. Опишем окружность радиусом АВ с центром В и на ней, отправляясь от A, как раньше, отмерим последовательно три дуги радиусом AB. Последняя точка С будет лежать на прямой АВ, причем мы будем иметь: АВ = ВС. Затем опишем окружность радиуса АВ с центром А и построим точку С', обратную точке С относительно этой окружности. Тогда получим:

АС'*АС = АВ2,

АС'*2АВ = АВ2,

2АС = АВ.

Рис. 44. Нахождение середины отрезка

Значит, С есть искомая середина отрезка.

2. Как разделить окружность на четыре, восемь, двенадцать частей?

Термины при построениях окружности

Окружностью называется замкнутая кривая линия, каждая точка которой расположена на одинаковом расстоянии от одной точки О, называемой центром.

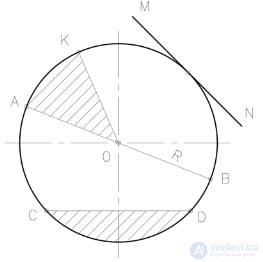
Прямые линии, соединяющие любую точку окружности с ее центром, называют радиусами R.

Прямая АВ, соединяющая две точки окружности и проходящая через ее центр О, называется диаметром D.

Части окружностей называются дугами.

Прямая СD, соединяющая две точки на окружности, называется хордой.

Прямая МN,которая имеет только одну общую точку с окружностью называется касательной.

Часть круга, ограниченная хордой СD и дугой, называется сигментом.

Часть круга, ограниченная двумя радиусами и дугой, называется сектором.

Две взаимно перпендикулярные горизонтальная и вертикальная линии, пересекающиеся в центре окружности, называются осями окружности.

Угол, образованный двумя радиусами КОА, называется центральным углом.

Два взаимно перпендикулярных радиуса составляют угол в 900 и ограничивают 1/4 окружности.

Деление окружности на 4 и 8 одинаковых частей

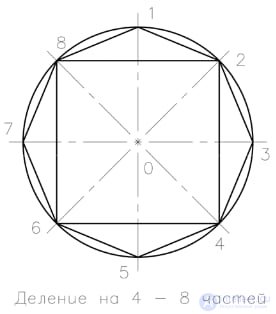
Проводим окружность с горизонтальной и вертикальной осями, которые делят ее на 4-ре равные части. Проведенные с помощью циркуля или угольника под 450, две взаимно перпендикулярные линии делят окружность на 8-мь равных частей.

---

Деление окружности на 3 и 6 равных частей (кратные 3 трем)

Для деления окружности на 3, 6 и кратное им количество частей, проводим окружность заданного радиуса и соответствующие оси. Деление можно начинать от точки пересечения горизонтальной или вертикальной оси с окружностью. Заданный радиус окружности последовательно откладывается 6-ть раз. Затем полученные точки на окружности последовательно соединяются прямыми линиями и образуют правильный вписанный шести-угольник. Соединение точек через одну дает равносторонний треугольник, и деление окружности на три равные части.

---

Деление окружности на 5 и 10 равных частей

Построение правильного пятиугольника выполняется следующим образом. Проводим две взаимно перпендикулярные оси окружности равные диаметру окружности. Делим правую половину горизонтального диаметра пополам с помощью дуги R1. Из полученной точки "а" в середине этого отрезка радиусом R2 проводим дугу окружности до пересечения с горизонтальным диаметром в точке "b". Радиусом R3 из точки "1" проводят дугу окружности до пересечения с заданной окружностью (т.5) и получают сторону правильного пятиугольника. Расстояние "b-О" дает сторону правильного десятиугольника.

---

Деление окружности на N-ное количество одинаковых частей (построение правильного многоугольника с N сторон)

Выполняется следующим образом. Проводим горизонтальную и вертикальную взаимно перпендикулярные оси окружности. Из верхней точки "1" окружности проводим под произвольным углом к вертикальной оси прямую линию. На ней откладываем равные отрезки произвольной длины, число которых равно числу частей на которое мы делим данную окружность, например 9. Конец последнего отрезка соединяем с нижней точкой вертикального диаметра. Проводим линии, параллельные полученной, из концов отложенных отрезков до пересечения с вертикальным диаметром, разделив таким образом вертикальный диаметр данной окружности на заданное количество частей. Радиусом равным диаметру окружности, из нижней точки вертикальной оси проводим дугу MN до пересечения с продолжением горизонтальной оси окружности. Из точек M и N проводим лучи через четные ( или нечетные) точки деления вертикального диаметра до пересечения с окружностью. Полученные отрезки окружности будут являться искомыми, т.к. точки 1, 2, …. 9 делят окружность на 9-ть ( N ) равных частей.

3. Раскройте принцип построения скругления углов.

Сопряжение двух пересекающихся прямых дугой заданного радиуса называют скруглением углов. Его выполнение можно увидеть на рис. 32. Параллельно сторонам угла, образованного данными прямыми, проводят вспомогательные прямые на расстоянии, равном радиусу. Точка пересечения вспомогательных прямых является центром дуги сопряжения.

Из полученного центра О опускают перпендикуляры к сторонам данного угла и на пересечении их получают точки сопряжения А и А'. Между этими точками проводят сопрягающую дугу радиусом R из центра О.

Рис. 32

Скругление прямого угла

Cкругление прямого угла, имеющего вершину О, дугой радиуса R осуществляется в следующей последовательности: 1. Из вершины О проводят дугу заданным радиусом R, до пересечения со сторонами угла в точках А и В (точки сопряжения); 2. Центр скругления О1 должен находится на геометрическом месте точек, равноудаленных от сторон угла, т.е. на биссектрисе угла АОВ и определяется точкой пересечения дуг радиуса R, проведенных из точек сопряжения А и В; 3. Проводят дугу АВ радиусом R и центром О1.

Скругление острого угла

Скругление острого угла дугой радиуса R можно выполнить в следующей последовательности: 1. Об этом говорит сайт https://intellect.icu . Геометрическим местом точек, равноудаленных от сторон угла, будут являться прямые, параллельные сторонам угла и проходящие от них на расстоянии R; 2. Точка пересечение этих прямых определяет центр скругления О1; 3. Пересечение перпендикуляров опущенных из центра скругления со сторонами определят положение точек сопряжения А и В; 4. Поводим дугу АВ из центра О1 радиусом R.

Скругление тупого угла

Скругление тупого угла производится точно так же, как и острого. Можно несколько изменить ход построения, если воспользоваться биссектрисой угла: 1. Строят биссектрису угла; 2. Проводят прямую, параллельную одной из сторон угла и отстоящую от нее на расстоянии R; 3. Точка пересечения этой прямой с биссектрисой определяет положение центра скругления О1; 4. Пересечение перпендикуляров опущенных из центра скругления со сторонами определят положение точек сопряжения А и В; 5. Поводим дугу АВ из центра О1 радиусом R.

4. Что такое сопряжение?

5. Какие виды сопряжения вы знаете?

Сопряжением называется плавный переход по кривой от одной линии к другой. Сопряжения бывают циркульные и лекальные. Построение их основано на свойствах касательных к кривым линиям. Сопряжение отрезков прямых с циркульными кривыми будет возможно, если точка сопряжения является одновременно и точкой касания прямой к дуге кривой. Следовательно, радиус сопряжения должен быть перпендикулярным к прямой в точке касания. Сопряжение циркульных кривых возможно тогда, когда точка сопряжения будет являться одновременно и точкой касания сопрягаемых дуг. Следовательно, точка касания должна находиться на линии центров дуг окружностей. Сопряжение пересекающихся прямых: Пример 1. Даны пересекающиеся прямые AB и ВС и радиус сопряжения R; требуется выполнить сопряжение прямых (фиг. 66, а, б, в). Сопряжение будет возможным, если прямые AB и ВС будут касательными к окружности радиуса R. Для нахождения центра этой окружности необходимо провести на расстоянии R параллельно заданным прямым вспомогательные прямые до их взаимного пересечения в точке 0. Из точки О, как из центра, проводится дуга радиуса R. Точками сопряжения будут точки M и Н, определяемые пересечением прямых AB и ВС с опущенными на них перпендикулярами из точки О. Пример 2. Даны пересекающиеся прямые AB и ВС и радиусы сопряжения R и R1 Построение сопряжения возможно, если угол а<90. Способ построения такого сопряжения приведен на фиг. 66,г. Сопряжение параллельных прямых Пример 1. Даны две параллельные прямые AB и СЕ и точки сопряжения В и С (фиг. 67). Надо построить плавное сопряжение циркульными кривыми так, чтобы оно проходило через заданную точку K, посредине отрезка ВС. Для определения радиусов и центров дуг сопряжения делим отрезки BK и КС прямыми так, чтобы они были перпендикулярны этим отрезкам и делили их пополам. Так как радиус сопряжения должен быть перпендикулярным к прямой в точке сопряжения, то для нахождения центров О дуг сопряжения восстанавливаем из точек В и С перпендикуляры до пересечения их с ранее проведенными перпендикулярами к прямой ВС. Точки пересечения этих перпендикуляров определят положение центров сопряжений О—О, а равные между собой отрезки 05 и ОС дадут величины радиусов сопряжений. Пример 2 (фиг. 68), Этот пример отличается от предыдущего тем, что точка К взята на прямой ВС произвольно, на некотором расстоянии e от прямой СЕ; следовательно, радиусы сопряжений R и R1— разные по величине. Ход построения сопряжений такой же, как и в предыдущем примере. П p и м e p 3. Даны: расстояние между двумя параллельными прямыми AB и СЕ, равное сумме сопрягаемых радиусов R и R1, и точка сопряжения В (фиг. 69). Для построения сопряжения проводим параллельно AB на расстоянии R вспомогательную прямую 0—01. Центр сопряжения 0 для радиуса R будет находиться на пересечении перпендикуляра, проведенного из точки В к вспомогательной прямой. Описывая из точки О дугу радиусом R, найдем точку К, из которой радиусом R1 делаем на вспомогательной прямой засечку, определяющую центр сопряжения O1. Из точки О1 опускаем перпендикуляр на прямую СЕ и, найдя точку сопряжения С, сопрягаем точки К и С дугой радиуса R1. Сопряжение дуги окружности с прямой Пример 1. Построим сопряжение дуги радиуса R с прямой AB радиусом R1 (фиг. 70). Для этого необходимо найти центр сопряжения 0 и точки сопряжения С и а. Точка С является одновременно точкой их касания и должна лежать на линии центров этих дуг. Радиус сопряжения должен быть перпендикулярен к прямой AB в точке касания а. Поэтому из центра О описываем радиусом, равным сумме R+R1, дугу. На ней будет находиться центр сопряжения 0, для определения которого проводим параллельно AB на расстоянии R1 вспомогательную прямую ее до пересечения с проведенной дугой. Соединив точки O1 и О, найдем точку сопряжения С. Для определения точки а опускаем из О1 перпендикуляр на AB. Далее, радиусом R1 из центра O1 сопрягаем точки а и С. Пример 2. Даны: дуга радиуса R, прямая AB и точка сопряжения а. Требуется найти точку сопряжения С и радиус сопряжения R1 (фиг. 71). Проводим через точку а перпендикуляр к AB, на котором откладываем вниз отрезок aK, равный R. Соединяем центр О с точкой К. Для нахождения центра сопряжения O1 проводим через середину отрезка OK перпендикулярную прямую, которая пересечется с прямой aK в точке O1 Соединив О1 с О, найдем точку сопряжения С. Сопряжение дуг окружностей дугой окружности Сопряжение дуг окружностей может быть внешним (фиг. 72) или внутренним (фиг. 73). В обоих случаях сопряжения выполнимы: 1) если расстояние С между центрами О и 01 сопрягаемых дуг больше суммы их радиусов R и R1 (фиг. 72, а и 73, а), т.е. C>R+R1 и 2) когда C=C+R1 или R1>=C+R. Для внешнего сопряжения дуг сопряжение окажется также невозможно, если радиус сопрягающей дуги R2 будет меньше полуразности С — (R+R1), т. е. R2 < <(C-(R+R1))/2. Во всех случаях решение задачи сводится к нахождению центра 02 сопрягающей дуги радиуса R2 и точек сопряжения A и В. Внешнее сопряжение. Даны: дуги радиусов R и R1 расстояние С между центрами этих дуг и радиус сопряжения R2 (фиг. 72,a). Требуется построить сопряжение при условии, что C>R+R1. Для построения сопряжения необходимо определить центр 02 и точки сопряжения Л и В. Для нахождения центра 02 проводим из центра О дугу радиуса R2+R, а из центра О1 дугу радиуса R2+R1 Пересечение этих дуг определит центр 02. Соединив прямыми центры О и 01 с центром 02, найдем на пересечении этих прямых с соответствующими дугами точки сопряжения A и В. Полученные точки сопрягаем радиусом R2. Построение сопряжения для случая, когда C Внутреннее сопряжение. Даны: дуги радиусов R и R1 расстояние С между центрами этих дуг и радиус сопряжения R2 (фиг. 73, а). Требуется построить сопряжение, если C>R+R1 Решение этой задачи такое же, как и предыдущей, с той лишь разницей, что из центров О и О1 проводятся дуги радиусами R2 - R и R2 - R1. На фиг. 73, б приведено построение сопряжения для случая, когда C

6. Какие элементы определяют сопряжение?

7. Какие кривые второго порядка вы знаете?

Общим уравнением второго порядка называется уравнение вида:

Ax2+2Bxy+Cy2+2Dx+2Ey+F=0

где коэффициенты A,B,C одновременно не равны нулю.
Линии, определяемые такими уравнениями, называются кривыми второго порядка.
Центром некоторой линии называется такая точка плоскости, по отношению к которой точки этой линии расположены симметрично парами.
Линии второго порядка, обладающие единственным центром, называются центральными.
Координаты центра S(x0 ; y0) линии определяются из системы:

Обозначим через .
При Δ≠0 кривая второго порядка будет центральной.
Причем, при Δ>0 уравнение является уравнением эллиптического типа. Каждое эллиптическое уравнение является уравнением либо обыкновенного эллипса, либо вырожденного эллипса (точка), либо мнимого эллипса (в этом случае уравнение не определяет на плоскости никакого геометрического образа).
При Δ<0 уравнение является уравнением гиперболического типа. Каждое гиперболическое уравнение определяет либо обыкновенную гиперболу, либо вырожденную (пару пересекающихся прямых).
При Δ=0 линия второго порядка не является центральной. Такие уравнения называются уравнениями параболического типа и определяют на плоскости либо обыкновенную параболу, либо пару параллельных (или совпадающих) прямых, либо не определяют на плоскости никакого геометрического образа
Классификация кривых второго порядка:

• Эллипс
• Окружность
• Гипербола
• Парабола

Оптические свойства кривых второго порядка:

Для эллипса: лучи света, исходящие из одного фокуса эллипса, после зеркального отражения от эллипса проходят через второй фокус.

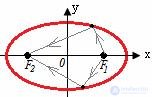
Для гиперболы: продолжение отраженного луча света, исходящего из одного фокуса гиперболы, попадает во второй фокус.

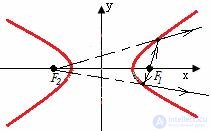
Для параболы: лучи света, исходящие из фокуса параболы, после зеркального отражения от нее образуют пучок лучей, параллельных ее фокальной оси.

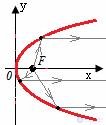
Уравнение в полярных координатах.
Полярное уравнение, общее по форме для эллипса, одной ветви гиперболы и параболы имеет вид:

где φ,ρ - полярные координаты произвольной точки линии, p –параметр, ε - эксцентриситет. При этом полярная система координат выбрана следующим образом: полюс находится в фокусе, полярная ось направлена в сторону, противоположную ближайшей к этому фокусу директрисы.
В частности, при ε=0, получим уравнение окружности в полярных координатах:
ρ=R

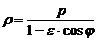
8. Что такое овал?

Овал

Овал – замкнутая коробовая кривая, имеющая две оси симметрии. Коробовой кривой называется односторонне выпуклая замкнутая или незамкнутая линия, состоящая из сопряженных дуг окружностей разных радиусов. Многие детали машин, приборов и аппаратов имеют контур очертания, состоящий из прямых линий и дуг окружностей с плавными переходами от одной линии к другой.

9. Дайте определения лекальных кривых.

Лекальными называют плоские кривые, вычерченные с помощью лекал по предварительно построенным точкам. К лекальным кривым относят: эллипс, параболу, гиперболу, циклоиду, синусоиду, эвольвенту и др.

10. Раскройте принципы построения эллипса.

Эллипс представляет собой замкнутую плоскую кривую второго порядка. Она характеризуется тем, что сумма расстояний от любой ее точки до двух точек фокусов есть величина постоянная, равная большей оси эллипса. Построить эллипс можно несколькими способами. Например, можно построить эллипс по его большой АВ и малой CD осям (рис. 37, а). На осях эллипса как на диаметрах строят две окружности, которые можно разделить радиусами на несколько частей. Через точки деления большой окружности проводят прямые, параллельные малой оси эллипса, а через точки деления малой окружности - прямые, параллельные большой оси эллипса. Точки пересечения этих прямых и являются точками эллипса.

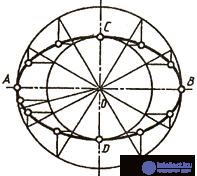
Рис. 37, а

Можно привести пример построения эллипса по двум сопряженным диаметрам (рис. 37, б) MN и KL. Сопряженными два диаметра называют, если каждый из них делит пополам хорды, параллельные другому диаметру. На сопряженных диаметрах строят параллелограмм. Один из диаметров MN делят на равные Части; на такие же части делят и стороны параллелограмма, параллельные другому диаметру, нумеруя их, как показано на чертеже. Из концов второго сопряженного диаметра KL через точки деления проводят лучи, в пересечении которых получают точки эллипса.

11. Какая кривая называется параболой?

Параболой называют незамкнутую кривую второго порядка, все точки которой равно удалены от одной точки - фокуса и от дйиной прямой - директрисы.

Рассмотрим пример построения параболы по ее вершине О и какой-либо точке В (рис. 38, а). С этой целью строят прямоугольник ОАВС и делят его стороны на равные части, из точек деления проводят лучи. В пересечении одноименных лучей получают точки параболы.

Рис. 38, а

Можно привести пример построения параболы в виде кривой, касательной прямым с заданными на них точками А и В (рис. 38, б). Стороны угла, образованного этими прямыми, делят на равные части и нумеруют точки деления. Одноименные точки соединяют прямыми. Параболу вычерчивают как огибающую зтак прямых.

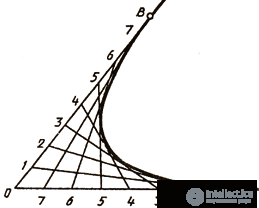
12. Какая кривая называется гиперболой?

Гиперболой называют плоскую незамкнутую кривую второго порядка, состоящую из двух веток, концы которых удаляются в бесконечность, стремясь к своим ассимптотам. Гипербола отличается тем, что каждая точка ее обладает особым свойством: разность ее расстояний от двух данных точек-фокусов есть величина постоянная, равная расстоянию между вершинами кривой. Если ассимптоты гиперболы взаимно перпендикулярны, она называется равнобокой. Равнобокая гипербола широко применяется для построения различных диаграмм, когда задана своими координатами одна точка М (рис. 38, в). В этом случае через заданную точку проводят линии АВ и KL параллельно координатным осям. Из полученных точек пересечения проводят линии, параллельные координатным осям. В их пересечении получают точки гиперболы.

Рис. 38, в

13. Дайте определение циклоиды.

Рис. 38, в

Циклоидой называют кривую линию, представляющую собой траекторию точки А при перекатывании окружности (рис. 39). Для построения циклоиды от исходного положения точки А откладывают отрезок АА1 отмечают промежуточное положение точки А. Так, в пересечении прямой, проходящей через точку l, окружностью, описанной из центра О1, получают первую точку циклоиды. Соединяя плавной прямой построенные точки, Получают циклоиду.

Рис. 39

14. Раскройте принципы построения синусоиды.

Синусоидой называют плоскую кривую, изображающую изменение синуса в зависимости от изменения его угла. Для построения синусоиды (рис. 40) нужно разделить окружность на равные части и на такое же количество равных частей разделить отрезок прямой АВ = 2nR. Из одноименных точек деления провести взаимно перпендикулярные линии, в пересечении которых получают точки, принадлежащие синусоиде.

15. Какая плоская кривая называется эвольвентой?

Эвольвентой называют плоскую кривую, являющуюся траекторией любой точки прямой линии, перекатываемой по окружности без скольжения. Построение эвольвенты выполняют в следующем порядке (рис. 41): окружность делят на равные части; проводят касательные к окружности, направленные в одну сторону и проходящие через каждую точку деления; на касательной, проведенной через последнюю точку деления окружности, откладывают отрезок, равный длине окружности 2πR, который делят на столько же равных частей. На первой касательной откладывают одно деление 2πR/n, на второй - два и т. д. Полученные точки соединяют плавной кривой и получают эвольвенту окружности.

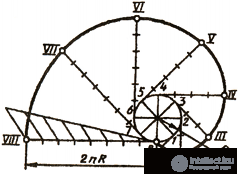
Рис. 41

Тебе нравиться вопросы для самопроверки по начертательной геометрии с ответами? или у тебя есть полезные советы и дополнения? Напиши другим читателям ниже. Надеюсь, что теперь ты понял что такое вопросы для самопроверки по начертательной геометрии с ответами и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Начертательная геометрия и инженерная графика

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.