Лекция
Сразу хочу сказать, что здесь никакой воды про теория массового обслуживания, и только нужная информация. Для того чтобы лучше понимать что такое теория массового обслуживания, смо , настоятельно рекомендую прочитать все из категории Теория массового обслуживания.
1. смо с отказами, пример, характеристики
2 . СМО с ожиданием (неограниченным ожиданием или очередью), пример, характеристики
3. СМО смешанного типа (с ограниченным ожиданием
Сложный характер рыночной экономики и современный уровень предъявляемых к
ней требований стимулируют использование более серьезных методов анализа ее теоретических и практических проблем. В последние десятилетия значительный вес в экономических
исследованиях приобрели математические методы. Математическое моделирование все более и более становится одним из основных и наиболее плодотворных методов изучения экономических процессов и объектов. Математический анализ экономических задач органично
превращается в часть экономики. Положительная оценка этого подтверждается и тем, что
начиная с 1969 г. Нобелевские премии в области экономики присуждаются, как правило, за
экономико-математические исследования.
Одним из важных разделов экономико-математического моделирования является
теория массового обслуживания , представляющая собой теоретические основы эффективного конструирования и эксплуатации систем массового обслуживания. Системы массового
обслуживания (СМО) встречаются во многих областях экономики (производство, техника,
военная область, быт и др.) и предназначены для многократного использования при выполнении однотипных задач.
В борьбу за клиента в современной экономике вкладываются огромные средства. По
оценкам западных экономистов, завоевание фирмой нового клиента обходится ей в 6 раз дороже, чем удержание существующих покупателей. А если клиент ушел неудовлетворенным,
то на его возвращение приходится потратить в 25 раз больше средств. Во многих случаях неудовлетворенность клиента вызвана неудачной организацией его обслуживания (слишком
долгое ожидание в очереди, отказ в обслуживании и т.д.). Использование теории массового
обслуживания позволяет фирме избежать подобных неприятностей.
Основоположником теории массового обслуживания считается датский ученый А. К.
Эрланг. Являясь сотрудником Копенгагенской телефонной компании, он опубликовал в 1909
году работу «Теория вероятностей и телефонные переговоры», в которой решил ряд задач по
теории систем массового обслуживания с отказами.
Значительный вклад в создание и разработку общей теории массового обслуживания
внес выдающийся советский математик Александр Яковлевич Хинчин (1984 – 1959), который предложил сам термин теория массового обслуживания. В зарубежной литературе чаще
используется название теория очередей.

Во многих областях производства, бытового обслуживания, экономики и финансов
важную роль играют системы1 специального вида, реализующие многократное выполнение
однотипных задач. Подобные системы называют системами массового обслуживания
(СМО). В качестве примеров СМО в финансово-экономической сфере можно привести системы, представляющие собой банки, страховые организации, налоговые инспекции, аудиторские службы. В сфере производства и обслуживания примерами СМО могут служить: различные системы связи (в том числе телефонные станции), погрузочно-разгрузочные комплексы (порты, товарные станции), автозаправочные станции, магазины, парикмахерские,
билетные кассы, пункты обмена валюты, ремонтные мастерские, больницы и т.д. Такие системы как компьютерные сети, системы сбора, хранения и обработки информации, транспортные системы, автоматизированные производственные участки и, в военной области,
системы противовоздушной или противоракетной обороны также могут рассматриваться как
своеобразные СМО.
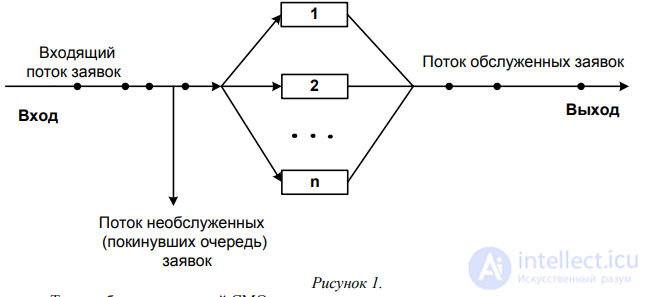
Схема СМО рис 1.
Каждая СМО включает в свою структуру некоторое число обслуживающих устройств
(единиц, приборов, линий), которые называют каналами обслуживания. Роль каналов могут
играть лица, выполняющие те или иные операции (кассиры, операторы, продавцы, парикмахеры и т.д.), линии связи, автомашины, краны, ремонтные бригады, железнодорожные пути, бензоколонки и т.д.
Каждая СМО предназначена для обслуживания (выполнения) некоторого потока заявок (или требований), поступающих на вход системы большей частью не регулярно, а в
случайные моменты времени. Обслуживание заявок, в общем случае, также длится не постоянное, заранее известное, а случайное время. После обслуживания заявки канал освобождается и готов к приему следующей заявки. Случайный характер потока и времени их обслуживания приводит к неравномерной загруженности СМО: в некоторые промежутки времени
на входе СМО могут скапливаться необслуженные заявки (они либо становятся в очередь,
либо покидают СМО необслуженными), в другие же периоды при свободных каналах на
входе СМО заявок не будет, что приводит к недогрузке СМО, т.е. к простаиванию каналов.
Схема СМО изображена на рисунке 1.
Таким образом, во всякой СМО можно выделить следующие основные элементы:
1) входящий поток заявок;
2) очередь;
3) каналы обслуживания;
4) выходящий поток обслуженных заявок.
Каждая СМО в зависимости от своих параметров: характера потока заявок, числа каналов обслуживания и их производительности, а также от правил организации работы, обладает определенной эффективностью функционирования (пропускной способностью), позволяющей ей более или менее успешно справляться с потоком заявок.
Предметом изучения теории массового обслуживания являются СМО.

Цель теории массового обслуживания – выработка рекомендаций по рациональному
построению СМО, рациональной организации их работы и регулированию потока заявок для
обеспечения высокой эффективности функционирования СМО.
Для достижения этой цели ставятся задачи теории массового обслуживания, состоящие в установлении зависимостей эффективности функционирования СМО от ее организации (параметров): характера потока заявок, числа каналов и их производительности и правил
работы СМО.
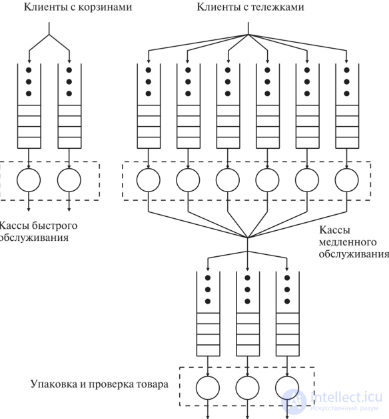
Рис. 15.3. Схема обслуживания в супермаркете
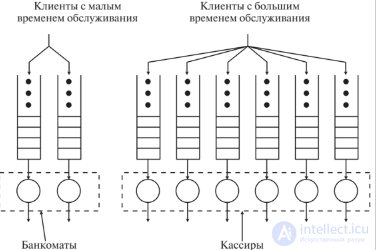
Рис. 15.2. Схема обслуживания в банке



В качестве характеристик эффективности функционирования СМО можно выбрать
три основные группы (обычно средних) показателей:
1. Показатели эффективности использования СМО:
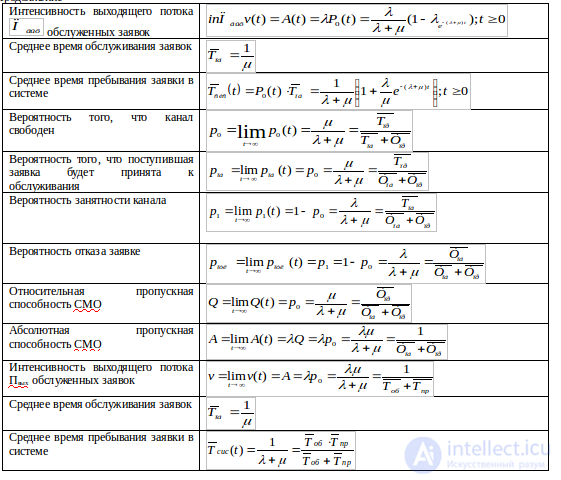
1.1. Абсолютная пропускная способность СМО – среднее число заявок, которое сможет обслужить СМО в единицу времени.
1.2. Относительная пропускная способность СМО – отношение среднего числа заявок,
обслуживаемых СМО в единицу времени, к среднему числу поступивших за это же
время заявок.
1.3. Средняя продолжительность периода занятости СМО.
1.4. Коэффициент использования СМО – средняя доля времени, в течение которого
СМО занята обслуживанием заявок, и т.п.
2. Показатели качества обслуживания заявок:
2.1. Среднее время ожидания заявки в очереди.
2.2. Среднее время пребывания заявки в СМО.
2.3. Вероятность отказа заявке в обслуживании без ожидания.
2.4. Вероятность того, что вновь поступившая заявка немедленно будет принята к обслуживанию.
2.5. Закон распределения времени ожидания заявки в очереди.
2.6. Закон распределения времени пребывания заявки в СМО.
2.7. Среднее число заявок, находящихся в очереди.
2.8. Среднее число заявок, находящихся в СМО, и т.п.
3. Показатели эффективности функционирования пары «СМО – клиент», где под «клиентом» понимают всю совокупность заявок или некий их источник. К числу таких показателей относится, например, средний доход, приносимый
СМО в единицу времени, и т.п.
Случайный характер потока заявок и длительности их обслуживания порождает в
СМО случайный процесс.
Определение. Об этом говорит сайт https://intellect.icu . Случайным процессом (или случайной функцией) называется соответствие, при котором каждому значению аргумента (в данном случае – моменту из промежутка
времени проводимого опыта) ставится в соответствие случайная величина (в данном случае
– состояние СМО).
Поэтому для решения задач теории массового обслуживания необходимо изучить
случайный процесс, протекающий в СМО, т.е. необходимо построить и проанализировать
его математическую модель. Математический анализ работы СМО существенно упрощается,
если этот случайный процесс удовлетворяет определенным условиям, которые будут рассмотрены ниже.



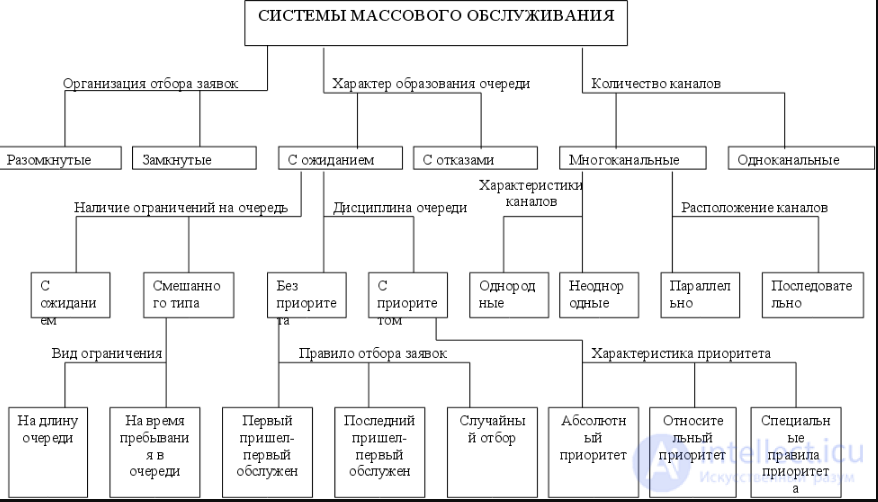
Системы массового обслуживания делятся на типы (или классы) по ряду признаков.
По числу каналов СМО подразделяют на одноканальные (когда имеется один канал
обслуживания) и многоканальные, точнее n -канальные (когда количество каналов n ≥ 2).
Здесь и далее будем полагать, что каждый канал одновременно может обслуживать только
одну заявку и, если не оговорено специально, каждая находящаяся под обслуживанием заявка обслуживается только одним каналом. Многоканальные СМО могут состоять из однородных каналов, либо из разнородных, отличающихся длительностью обслуживания одной заявки. Практически время обслуживания каналом одной заявки Tоб является непрерывной случайной величиной. Однако при условии абсолютной однородности поступающих заявок
и каналов время обслуживания может быть и величиной постоянной (T об = const ).


По дисциплине обслуживания СМО подразделяют на три класса:
1. СМО с отказами, в которых заявка, поступившая на вход СМО в момент, когда все
каналы заняты, получает «отказ» и покидает СМО («пропадает»). Чтобы эта заявка все же
была обслужена, она должна снова поступить на вход СМО и рассматриваться при этом как
заявка, поступившая впервые. Примером СМО с отказами может служить работа АТС: если
набранный телефонный номер (заявка, поступившая на вход) занят, то заявка получает отказ,
и, чтобы дозвониться по этому номеру, следует его набрать еще раз (заявка поступает на
вход как новая).
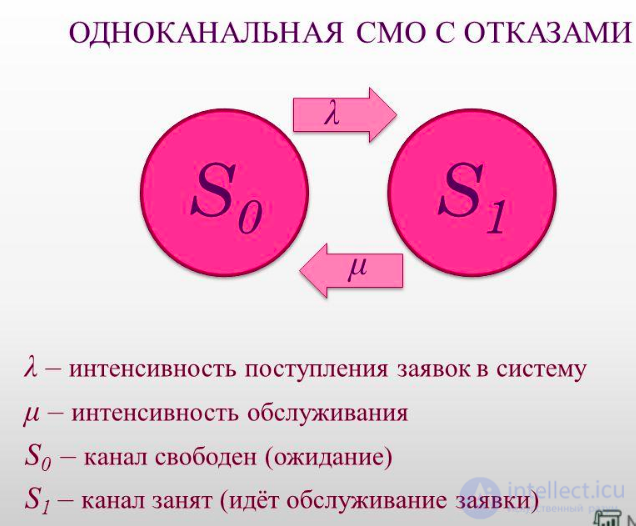
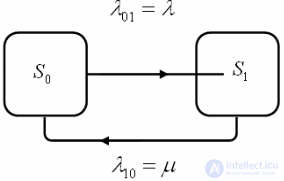
Рисунок 3. Граф состояний одноканальной СМО с отказами.
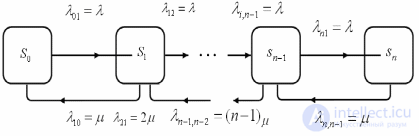
Рисунок 4. Граф состояний многоканальной СМО с отказами.
Характеристики одноканальной СМО с отказами.



2. СМО с ожиданием (неограниченным ожиданием или очередью). В таких системах
заявка, поступившая в момент занятости всех каналов, становится в очередь и ожидает освобождения канала, который примет ее к обслуживанию. Каждая заявка, поступившая на вход,
в конце концов будет обслужена. Такие СМО часто встречаются в торговле, в сфере бытового и медицинского обслуживания, на предприятиях (например, обслуживание станков бригадой наладчиков).

Рисунок 6. Граф состояний одноканальной СМО с ожиданием.
Состояния СМО имеют следующую интерпретацию:
S0 - канал свободен;
S1 - канал занят (очереди нет);
S2 - канал занят (одна заявка стоит в очереди);
Sn - канал занят (n-1 заявок стоит в очереди);
SN - канал занят (N-1 заявок стоит в очереди).
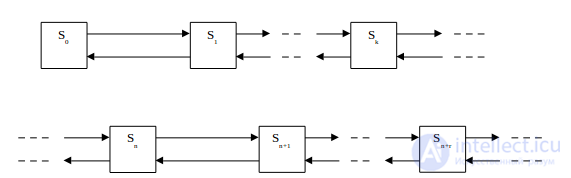
Рисунок 7. Граф состояний многоканальной СМО с ожиданием.
Обратим внимание, что по мере увеличения в СМО от 0 до n увеличивается число каналов обслуживания. При числе заявок в СМО, большем, чем n, интенсивность потока обслуживания сохраняется равной nµ.
Определим характеристики одноканальной СМОс ожиданием и ограниченной длиной очереди, равной (N —1):

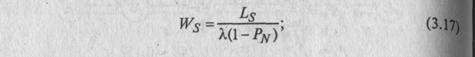
Рассмотрим пример одноканальной СМО с ожиданием.
Пример 3.2. Специализированный пост диагностики представляет собой одноканальную СМО. Число стоянок для автомобилей, ожидающих проведения диагностики, ограничено и равно 3 [(N- 1) = 3]. Если все стоянки заняты, т. е. в очереди уже находится три автомобиля, то очередной автомобиль, прибывший на диагностику, в очередь на обслуживание не становится. Поток автомобилей, прибывающих на диагностику, распределен по закону Пуассона и имеет интенсивность l= 0,85 (автомобиля в час). Время диагностики автомобиля распределено по показательному закону и в среднем равно 1,05 час.
Требуется определить вероятностные характеристики поста диагностики, работающего в стационарном режиме.
Решение
1. Параметр потока обслуживании автомобилей:
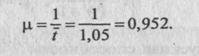
2. Приведенная интенсивность потока автомобилей определяется как отношение интенсивностей l и m, т. е.
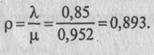
3. Вычислим финальные вероятности системы:
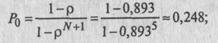
P1=ρ·P0 = 0.893·0.248 = 0.221
P2=ρ2·P0 = 0.8932·0.248 = 0.198
P3=ρ3·P0 = 0.8933·0.248 = 0.177
P4=ρ4·P0 = 0.8932·0.248 = 0.158
4. Вероятность отказа в обслуживании автомобиля:
Pотк=P4=ρ4·P0 ≈ 0.158
5. Относительная пропускная способность поста диагностики:
q=1-Pотк = 1-0.158 = 0.842
6. Абсолютная пропускная способность поста диагностики
A=λ·q = 0.85·0.842 = 0.716 (автомобиля в час)
7. Среднее число автомобилей, находящихся на обслуживании и в очереди (т.е. в системе массового обслуживания):
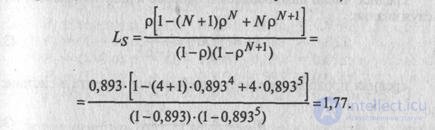
8. Среднее время пребывания автомобиля в системе:
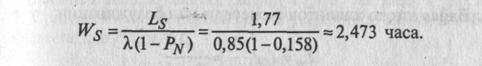
9. Средняя продолжительность пребывания заявки в очереди на обслуживание:
Wq=WS-1/μ = 2.473-1/0.952 = 1.423 часа
10. Среднее число заявок в очереди (длина очереди): Lq= А,(1 - PN) Wq= 0,85
Lq=λ(1-PN)·Wq = 0.85·(1-0.158)·1.423 = 1.02
Работу рассмотренного поста диагностики можно считать удовлетворительной, так как пост диагностики не обслуживает автомобили в среднем в 15,8% случаев (Ротк= 0,158).
3. СМО смешанного типа (с ограниченным ожиданием). Это такие системы, в которых на пребывание заявки в очереди накладываются некоторые ограничения.
Эти ограничения могут накладываться на длину очереди, т.е. максимально возможное
число заявок, которые одновременно могут находиться в очереди. В качестве примера такой
системы можно привести мастерскую по ремонту автомобилей, имеющую ограниченную по
размерам стоянку для неисправных машин, ожидающих ремонта.
Ограничения ожидания могут касаться времени пребывания заявки в очереди, по истечению которого она выходит из очереди и покидает систему, либо касаться общего времени
пребывания заявки в СМО (т.е. суммарного времени пребывания заявки в очереди и под обслуживанием).
В СМО с ожиданием и в СМО смешанного типа применяются различные схемы обслуживания заявок из очереди. Обслуживание может быть упорядоченным, когда заявки из
очереди обслуживаются в порядке их поступления в систему, и неупорядоченным, при котором заявки из очереди обслуживаются в случайном порядке. Иногда применяется обслуживание с приоритетом, когда некоторые заявки из очереди считаются приоритетными и поэтому обслуживаются в первую очередь.
По ограничению потока заявок СМО делятся на замкнутые и открытые.
Если поток заявок ограничен и заявки, покинувшие систему, могут в нее возвращаться, то СМО является замкнутой, в противном случае – открытой. Классическим примером
замкнутой СМО служит работа бригады наладчиков в цеху. Станки являются источниками
заявок на обслуживание, и их количество ограничено, наладчики – каналы обслуживания.
После проведения ремонтных работ вышедший из строя станок снова становится источником заявок на обслуживание. В открытой СМО характеристики потока заявок не зависят от
того, в каком состоянии сама СМО (сколько каналов занято). В замкнутой СМО – зависят.
Так, в рассмотренном выше примере интенсивность потока «заявок» со стороны станков (т.е.
количество заявок в единицу времени) зависит от того, сколько их неисправно и ждет наладки.
По количеству этапов обслуживания СМО делятся на однофазные и многофазные
системы. Если каналы СМО однородны, т.е. выполняют одну и ту же операцию обслуживания, то такие СМО называются однофазными. Если каналы обслуживания расположены последовательно и они неоднородны, так как выполняют различные операции обслуживания
(т.е. обслуживание состоит из нескольких последовательных этапов или фаз), то СМО называется многофазной. Примером работы многофазной СМО является обслуживание автомобилей на станции технического обслуживания (мойка, диагностирование и т.д.). Далее будем
рассматривать только однофазные СМО.
Строение максимально эффективных очередей и взгляд на проблемы с точки зрения балансировки нагрузки. Что такое балансировка нагрузки? По отпределению из Wikipedia это: “…методология распределения запросов на несколько компьютеров … озволяющая достичь оптимальной утилизации ресурсов, максимизировать пропускную способность системы, минимизировать время ответа на запрос, и избежать перегрузки”
Что здесь важно?
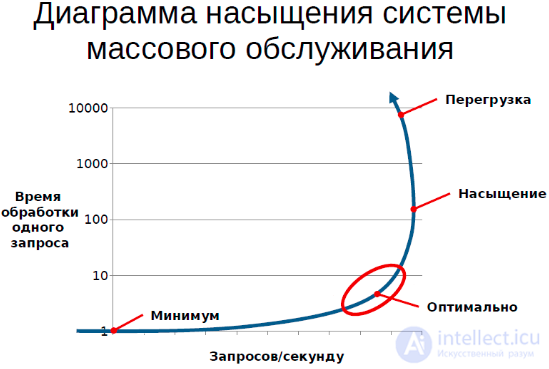
График – диаграмма насыщения. С одной стороны количество запросов в секунду, а с другой стороны – latency (в данном контексте – время обработки одного запроса).
Задача, когда мы организуем очередь, обработку очереди – это сделать так, чтобы у нас с одной стороны была высокая утилизация ресурсов, с другой стороны мы максимально качественно обслуживали всех клиентов.
Что такое качественно? В первую очередь, качество – это время обработки, время ожидания результата. И если посмотреть на типичную диаграмму системы, которую обслуживает очередь – она выглядит именно вот так. Т.е. можно строить график по latency, график можно строить по RPS. В RPS мы можем либо заметить, либо не заметить снижения RPS. Есть большое количество систем, в которых количество запросов в секунду снижается с увеличением нагрузки.
Что происходит с точки зрения системы массового обслуживания? Она выполняет бесполезную работу, т.е. в момент перегрузки происходит что-то, что не направлено так или иначе на непосредственное обслуживание клиентов, а направлено на борьбу с перегрузками. Например, если взять базу данных, типичным примером в БД является снижение нагрузки, снижение производительности при увеличении количества одновременно присутствующих в БД транзакций. Это происходит за счет того, что появляется ожидание на блокировках и deadlock’и. Ожидание на блокировке – это бесполезное дело, deadlock’и, вообще, приводят к тому, что транзакции рестартуют и их нужно выполнять повторно – пример из компьютерной системы.
В данной ситуации нас интересует построение такой системы, которая будет находиться в оптимальной части кривой, т.е. она будет выполнять максимально возможное количество запросов, при этом сохраняя свои тактико-технические характеристики.
В этом смысле часто осознаешь, что многие часто не до конца понимают, что их интересует, потому что latency и RPS – это не связанные вещи. Т.е. наше желание максимизировать производительность системы и наше желание максимизировать качество обслуживания – это противоречивые желания.
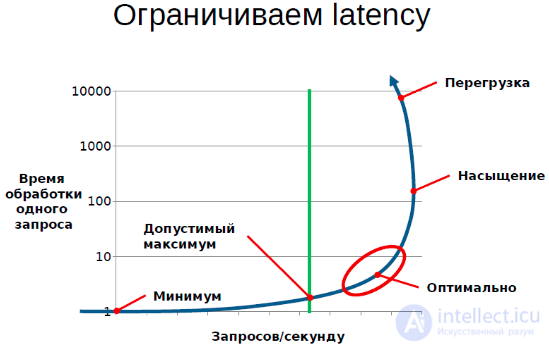
На графике качественно видно, что если мы хотим ограничить именно latency вот этой величиной, то мы можем, максимум, допустить вот такую нагрузку, дальше мы уже заходить не можем, т.е. дальше требования к качеству обслуживания фактически ограничивают пропускную способность.
Второй критерий, по которому мы можем оптимизировать систему – это максимизация RPS.

В этом смысле нам полезно дойти до какого-то насыщения системы, при этом сохранив удовлетворительный уровень обслуживания, и не выйти в область перегрузки.
Чтобы понять, почему это взаимосвязанные вещи, я попробую вгрызться в теорию очередей.

Модель с одним сервером – достаточно показательно.
Есть 2 способа понять, как работает система массового обслуживания:
Если пытаться вгрызться в теорию массового облуживания, то осознаешь, что моделей может быть очень много.
Нотация Кендалла

Есть нотация Кендалла – она классифицирует все системы по шести показателям:
Простейшая модель, которую теория очередей дает – это модель для одного сервера.

Что здесь дается? Степень утилизации – это соотношение производительности к темпу (скорости) поступления задач. Допустим, у нас 1 сервер может обслуживать 10 задач в секунду, а поступает 9 задач в секунду. Наверное, он справится с нагрузкой, в среднем 9 – это степень утилизации. Здесь хочется сказать – если количество задач в секунду превышает пропускную способность сервера, то пиши пропало, ничего особенного тут не поделаешь, очередь будет неизбежно расти.
πk – это вероятность k задач в очереди.
Что здесь интересно: допустим у вас 10 задач в очереди, скорость поступления задач – 10 в секунду, а сервер может обслужить 12 в секунду. Какова вероятность того, что в тот момент, когда придет следующий потребитель, очередь будет пуста, т.е. он сможет получить обслуживание немедленно? Это вероятность того, что до этого никто не пришел – это 2/12. С большой вероятностью, уже к тому моменту, когда приходит следующая задача, сервер обслуживает какую-то предыдущую с вероятностью 10/12, а с обратной вероятностью он никого не обслуживает – это нам говорит модель из теории массового обслуживания. Т.е. если мы хотим максимизировать утилизацию, то у нас неизбежно будет расти очередь, потому что в тот момент, когда новая задача поступает, сервер уже занят обслуживанием какой-то задачи, и чем выше утилизация, тем выше эта вероятность. Это базовый инсайд теории массового обслуживания.

Здесь я не привожу модели для нескольких серверов, но базовая идея в том, что если у нас есть единая очередь и множество серверов, то мы дисперсию в распределении участников можем гасить тем, что все сервера получают равномерную нагрузку.

Результат симуляции, когда у нас есть 80%-ная загрузка на кластер, и синий график – это задача поступает в произвольный сервер по случайному закону, а красный график – это когда у нас есть глобальная очередь, и каждый сервер берет задачу из очереди, когда у него появляется возможность. С увеличением количества серверов latency снижается – это реальная симуляция.
1 – это длина очереди, когда у нас при 80% загрузке каждый сервер работает независимо. В среднем у него есть какая-то очередь. Когда он работает из глобальной очереди вероятность того, что в момент поступления нет доступного для выполнения задачи сервера – в пределах 0,1. Интуитивно понятно: у нас есть 10 воркеров и 8 задач на воркера в каждый момент времени. Вероятность, что у нас пришла задача и нет свободного воркера, маленькая. Если у нас есть 10 воркеров и на каждого своя задача, то вероятность повышается.
Какие еще инсайды из теории массового обслуживания можно взять?

Общая идея закона Литтла в том, что количество одновременно обслуживающихся задач пропорционально времени обслуживания и темпу поступления. Что в данном случае важно?

Если у вас система получает 1000 запросов в секунду, время обслуживания одного запроса – 1 мс. Средняя длина очереди в такой системе будет 10 (количество одновременных задач в системе). В целом, если это разные очереди, т.е. если у вас у каждого воркера своя очередь, то у вас средняя длина очереди может достигать 10-ти.
С точки зрения масштабирования вывод из этого следующий:

Для того чтобы пропорционально расти, нам нужно масштабировать работу более-менее линейно, увеличивать число серверов и количество одновременно обслуживающихся задач. Т.е. если у нас задача большая, то увеличением числа серверов не факт, что сможем увеличить нашу производительность. И за счет того, что нам приходится увеличивать число серверов, у нас общее количество задач в работе растет, соответственно растет время всяких прогревов, стоимость простоя и т.д. и т.п.

Вывод: у нас есть конфликт требований, и для того, чтобы его удовлетворить, нам нужно так или иначе снижать нагрузку на систему. Это основной вывод, который нам дает теория.
А как ты думаешь, при улучшении теория массового обслуживания, будет лучше нам? Надеюсь, что теперь ты понял что такое теория массового обслуживания, смо и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория массового обслуживания
Комментарии
Оставить комментарий
Теория массового обслуживания
Термины: Теория массового обслуживания