Лекция
Привет, Вы узнаете о том , что такое случайный процесс со счетным множеством состояний, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое случайный процесс со счетным множеством состояний , настоятельно рекомендую прочитать все из категории Теория массового обслуживания.
Случайный процесс, протекающий в системе массового обслуживания, состоит в том, что система в случайные моменты времени переходит из одного состояния в другое: меняется число занятых каналов, число заявок, стоящих в очереди, и т. п. Такой процесс существенно отличается от случайных процессов, которые мы рассматривали в главах 15-17. Дело в том, что система массового обслуживания представляет собой физическую систему дискретного типа с конечным (или счетным) множеством состояний, а переход системы из одного состояния в другое происходит скачком, в момент, когда осуществляется какое-то событие (приход новой заявки, освобождение канала, уход заявки из очереди и т. п.).
Рассмотрим физическую систему  со счетным множеством состояний
со счетным множеством состояний
 .
.
В любой момент времени 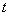 система
система  может быть в одном из этих состояний. Обозначим
может быть в одном из этих состояний. Обозначим 
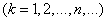 вероятность того, что в момент
вероятность того, что в момент 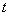 система будет находиться в состоянии
система будет находиться в состоянии 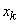 . Очевидно, для любого
. Очевидно, для любого 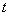
 . (19.2.1)
. (19.2.1)
Совокупность вероятностей  для каждого момента времени
для каждого момента времени 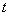 характеризует данное сечение случайного процесса, протекающего в системе. Эта совокупность не является исчерпывающей характеристикой процесса (она, например, совсем не отражает зависимости между сечениями), но все же достаточно хорошо описывает процесс и для ряда практических применений оказывается достаточной.
характеризует данное сечение случайного процесса, протекающего в системе. Эта совокупность не является исчерпывающей характеристикой процесса (она, например, совсем не отражает зависимости между сечениями), но все же достаточно хорошо описывает процесс и для ряда практических применений оказывается достаточной.
Случайные процессы со счетным множеством состояний бывают двух типов: с дискретным или непрерывным временем. Первые отличаются тем, что переходы из состояния в состояние могут происходить только в строго определенные, разделенные конечными интервалами моменты времени  . Об этом говорит сайт https://intellect.icu . Случайные процессы с непрерывным временем отличаются тем, что переход системы из состояния в состояние возможен в любой момент времени
. Об этом говорит сайт https://intellect.icu . Случайные процессы с непрерывным временем отличаются тем, что переход системы из состояния в состояние возможен в любой момент времени 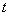 .
.
В качестве примера дискретной системы  , в которой протекает случайный процесс с непрерывным временем, рассмотрим группу из
, в которой протекает случайный процесс с непрерывным временем, рассмотрим группу из  самолетов, совершающих налет на территорию противника, обороняемую истребительной авиацией. Ни момент обнаружения группы, ни моменты подъема по ней истребителей заранее не известны. Различные состояния системы соответствуют различному числу пораженных самолетов в составе группы:
самолетов, совершающих налет на территорию противника, обороняемую истребительной авиацией. Ни момент обнаружения группы, ни моменты подъема по ней истребителей заранее не известны. Различные состояния системы соответствуют различному числу пораженных самолетов в составе группы:
 - не поражено ни одного самолета,
- не поражено ни одного самолета,
 - поражен ровно один самолет,
- поражен ровно один самолет,
………….
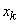 - поражено ровно
- поражено ровно 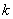 самолетов,
самолетов,
………….
 - поражены все
- поражены все  самолетов.
самолетов.
Схема возможных состояний системы и возможных переходов из состояния в состояние показана на рис. 19.2.1.

Рис. 19.2.1.
Стрелками показаны возможные переходы системы из состояния в состояние. Закругленная стрелка, направленная из состояния 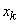 в него же, означает, что система может не только перейти в соседнее состояние, но и остаться в прежнем. Для данной системы характерны необратимые переходы (пораженные самолеты не восстанавливаются); в связи с этим из состояния
в него же, означает, что система может не только перейти в соседнее состояние, но и остаться в прежнем. Для данной системы характерны необратимые переходы (пораженные самолеты не восстанавливаются); в связи с этим из состояния  никакие переходы в другие состояния уже невозможны.
никакие переходы в другие состояния уже невозможны.
Отметим, что на схеме возможных переходов (рис. 19.2.1) показаны только переходы из состояния в соседнее состояние и не показаны «перескоки» через состояние: эти перескоки отброшены как практически невозможные. Действительно, для того чтобы система «перескочила» через состояние, нужно, чтобы строго одновременно были поражены два или более самолета, а вероятность такого события равна нулю.
Случайные процессы, протекающие в системах массового обслуживания, как правило, представляют собой процессы с непрерывным временем. Это связано со случайностью потока заявок. В противоположность системе с необратимыми переходами, рассмотренной в предыдущем примере, для системы массового обслуживания характерны обратимые переходы: занятый канал может освободиться, очередь может «рассосаться».
В качестве примера рассмотрим одноканальную систему массового обслуживания (например, одну телефонную линию), в которой заявка, заставшая канал занятым, не становится в очередь, а покидает систему (получает «отказ»). Это - дискретная система с непрерывным временем и двумя возможными состояниями:
 - канал свободен,
- канал свободен,
 - канал занят.
- канал занят.
Переходы из состояния в состояние обратимы. Схема возможных переходов показана на рис. 19.2.2.
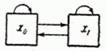
Рис. 19.2.2.
Для  -канальной системы такого же типа схема возможных переходов показана на рис. 19.2.3.
-канальной системы такого же типа схема возможных переходов показана на рис. 19.2.3.

Рис. 19.2.3.
Состояние  - все каналы свободны;
- все каналы свободны;  - занят ровно один канал,
- занят ровно один канал, 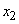 - занято ровно два канала и т. д.
- занято ровно два канала и т. д.
Рассмотрим еще один пример дискретной системы с непрерывным временем: одноканальную систему массового обслуживания, которая может находиться в четырех состояниях:
 - канал исправен и свободен,
- канал исправен и свободен,
 - канал исправен и занят,
- канал исправен и занят,
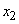 - канал неисправен и ждет ремонта,
- канал неисправен и ждет ремонта,
 - канал неисправен и ремонтируется.
- канал неисправен и ремонтируется.
Схема возможных переходов для этого случая показана на рис. 19.2.4.

Рис. 19.2.4.
Переход системы из  непосредственно в
непосредственно в  , минуя
, минуя  можно считать практически невозможным, так как для этого нужно, чтобы окончание ремонта и приход очередной заявки произошли строго в один и тот же момент времени.
можно считать практически невозможным, так как для этого нужно, чтобы окончание ремонта и приход очередной заявки произошли строго в один и тот же момент времени.
Для того чтобы описать случайный процесс, протекающий в дискретной системе с непрерывным временем, прежде всего нужно проанализировать причины, вызывающие переход системы из состояния в состояние. Для системы массового обслуживания основным фактором, обусловливающим протекающие в ней процессы, является поток заявок. Поэтому математическое описание любой системы массового обслуживания начинается с описания потока заявок.
Информация, изложенная в данной статье про случайный процесс со счетным множеством состояний , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое случайный процесс со счетным множеством состояний и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория массового обслуживания
Из статьи мы узнали кратко, но содержательно про случайный процесс со счетным множеством состояний
Комментарии
Оставить комментарий
Теория массового обслуживания
Термины: Теория массового обслуживания