Лекция
Привет, Вы узнаете о том , что такое система смешанного типа с ограничением по длине очереди, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое система смешанного типа с ограничением по длине очереди, смо , настоятельно рекомендую прочитать все из категории Теория массового обслуживания.
В предыдущем  мы рас
смо трели систему массового обслуживания с ограничением по времени пребывания в очереди. Здесь мы рассмотрим систему смешанного типа с другим видом ограничения ожидания - по числу заявок, стоящих в очереди. Предположим, что заявка, заставшая все каналы занятыми, становится в очередь, только если в ней находится менее
мы рас
смо трели систему массового обслуживания с ограничением по времени пребывания в очереди. Здесь мы рассмотрим систему смешанного типа с другим видом ограничения ожидания - по числу заявок, стоящих в очереди. Предположим, что заявка, заставшая все каналы занятыми, становится в очередь, только если в ней находится менее 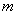 заявок; если же число заявок в очереди равно
заявок; если же число заявок в очереди равно 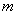 (больше
(больше 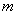 оно быть не может), то последняя прибывшая заявка в очередь не становится и покидает систему необслуженной. Остальные допущения - о простейшем потоке заявок и о показательном распределении времени обслуживания - оставим прежними.
оно быть не может), то последняя прибывшая заявка в очередь не становится и покидает систему необслуженной. Остальные допущения - о простейшем потоке заявок и о показательном распределении времени обслуживания - оставим прежними.
Итак, имеется  -канальная система с ожиданием, в которой количество заявок, стоящих в очереди, ограничено числом
-канальная система с ожиданием, в которой количество заявок, стоящих в очереди, ограничено числом 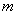 . Составим дифференциальные уравнения для вероятностей состояний системы. Заметим, что в данном случае число состояний системы будет конечно, так как общее число заявок, связанных с системой, не может превышать
. Составим дифференциальные уравнения для вероятностей состояний системы. Заметим, что в данном случае число состояний системы будет конечно, так как общее число заявок, связанных с системой, не может превышать 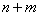 (
( обслуживаемых и
обслуживаемых и 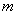 стоящих в очереди). Перечислим состояния системы:
стоящих в очереди). Перечислим состояния системы:
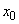 - все каналы свободны, очереди нет,
- все каналы свободны, очереди нет,
 - занят один канал, очереди нет,
- занят один канал, очереди нет,
………
 - занято
- занято  каналов, очереди нет,
каналов, очереди нет,
………
 - занято
- занято 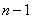 каналов, очереди нет,
каналов, очереди нет,
 - заняты все
- заняты все  каналов, очереди нет,
каналов, очереди нет,
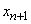 - заняты все
- заняты все  каналов, одна заявка стоит в очереди,
каналов, одна заявка стоит в очереди,
………
 - заняты все
- заняты все  каналов,
каналов, 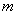 заявок стоит в очереди.
заявок стоит в очереди.
Очевидно, первые  уравнений для вероятностей
уравнений для вероятностей  будут совпадать с уравнениями Эрланга (19.8.8). Об этом говорит сайт https://intellect.icu . Выведем остальные уравнения. Имеем
будут совпадать с уравнениями Эрланга (19.8.8). Об этом говорит сайт https://intellect.icu . Выведем остальные уравнения. Имеем
 ,
,
откуда
 .
.
Далее выведем уравнение для 
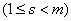
 ,
,
откуда
 .
.
Последнее уравнение будет
 .
.
Таким образом, получена система 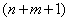 дифференциальных уравнений:
дифференциальных уравнений:
 (19.11.1)
(19.11.1)
Рассмотрим предельный случай при  . Приравнивая все производные нулю, а все вероятности считая постоянными, получим систему алгебраических уравнений
. Приравнивая все производные нулю, а все вероятности считая постоянными, получим систему алгебраических уравнений
 (19.11.2)
(19.11.2)
и добавочное условие:
 . (19.11.3)
. (19.11.3)
Уравнения (19.11.2) могут быть решены так же, как мы решили аналогичные алгебраические уравнения в предыдущих  . Не останавливаясь на этом решении, приведем только окончательные формулы:
. Не останавливаясь на этом решении, приведем только окончательные формулы:

 , (19.11.4)
, (19.11.4)

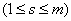 . (19.11.5)
. (19.11.5)
Вероятность того, что заявка покинет систему необслуженной, равна вероятности  того, что в очереди уже стоят
того, что в очереди уже стоят 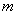 заявок.
заявок.
Нетрудно заметить, что формулы (19.11.4) и (19.11.5) получаются из формул (19.10.11), (19.10.12), если положить в них  и ограничить суммирование по
и ограничить суммирование по  верхней границей
верхней границей 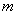 .
.
Пример. На станцию текущего ремонта автомашин поступает простейший поток заявок с плотностью  (машины в час). Имеется одно помещение для ремонта. Во дворе станции могут одновременно находиться, ожидая очереди, не более трех машин. Среднее время ремонта одной машины
(машины в час). Имеется одно помещение для ремонта. Во дворе станции могут одновременно находиться, ожидая очереди, не более трех машин. Среднее время ремонта одной машины 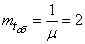 (часа). Определить: а) пропускную способность системы; б) среднее время простоя станции; в) определить, насколько изменятся эти характеристики, если оборудовать второе помещение для ремонта.
(часа). Определить: а) пропускную способность системы; б) среднее время простоя станции; в) определить, насколько изменятся эти характеристики, если оборудовать второе помещение для ремонта.
Решение. Имеем:  ,
,  ,
,  ,
,  .
.
а) По формуле (19.11.5), полагая  , находим вероятность того, что пришедшая заявка покинет систему необслуженной:
, находим вероятность того, что пришедшая заявка покинет систему необслуженной:
 .
.
Относительная пропускная способность системы 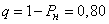 . Абсолютная пропускная способность:
. Абсолютная пропускная способность:  (машины в час).
(машины в час).
б) Средняя доля времени, которое система будет простаивать, найдем по формуле (19.11.4): 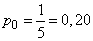 .
.
в) Полагая  , найдем:
, найдем:
 ,
,
 (т. е. удовлетворяться будет около 98% всех заявок).
(т. е. удовлетворяться будет около 98% всех заявок).
 (машины в час).
(машины в час).
Относительное время простоя:  , т. е. оборудование будет простаивать полностью около 34% всего времени.
, т. е. оборудование будет простаивать полностью около 34% всего времени.
Информация, изложенная в данной статье про система смешанного типа с ограничением по длине очереди , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое система смешанного типа с ограничением по длине очереди, смо и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория массового обслуживания
Из статьи мы узнали кратко, но содержательно про система смешанного типа с ограничением по длине очереди
Комментарии
Оставить комментарий
Теория массового обслуживания
Термины: Теория массового обслуживания