Расчет показателей эффективности одноканальной СМО с ограниченной очередью, примеры решения задач кратко

Привет, мой друг, тебе интересно узнать все про расчет показателей эффективности одноканальной смо с ограниченной очередью, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое расчет показателей эффективности одноканальной смо с ограниченной очередью, одноканальная смо с ограниченной очередью , настоятельно рекомендую прочитать все из категории Теория массового обслуживания.

Рассмотрим одноканальную систему массового обслуживания с ожиданием, в которую поступает
простейший поток заявок с интенсивностью X; интенсивность обслуживания и, (т.е. в среднем непрерывно
занятый канал будет выдавать 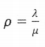обслуженных заявок в единицу (времени).
Длительность обслуживания - случайная величина, подчиненная показательному закону распределения.
Поток обслуживания является простейшим пуассоновским потоком событий.
Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания.
Предположим, что количество мест в очереди ограничено числом m, т.е. если заявка пришла в момент, когда в очереди
уже стоят m-заявок, она покидает систему не обслуженной.

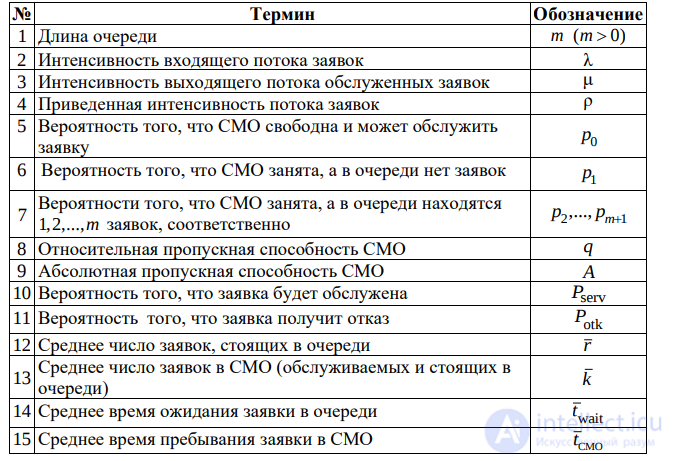
Список используемых терминов и обозначений

Поток обслуживания является простейшим пуассоновским потоком событий.
Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания.
Предположим, что количество мест в очереди ограничено числом m, т.е. если заявка пришла в момент, когда в очереди уже стоят m-заявок, она покидает систему не обслуженной.
В качестве показателей эффективности одноканальной
СМО с ограниченной длиной очереди будем рассматривать:
А - абсолютную пропускную способность СМО;
Q - относительную пропускную способность;
Ротк - вероятность отказа;
Lсист - среднее число находящихся в системе заявок;
Теист_ среднее время пребывания заявки в системе;
Lоч - средняя длина очереди;
Точ - среднее время ожидания в очереди.

Размеченный граф состояний представлен на рисунке 9.

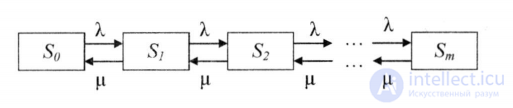
Рис. 9. Одноканальная СМ О с ограниченной длинной очереди

So - канал обслуживания свободен;
S1 - канал обслуживания занят, но очереди нет;
S2 - канал обслуживания занят, в очереди стоит 1 заявка;

***
Sm - канал обслуживания занят, в очереди все m заявок, любая следующая заявка получает отказ.
Вероятности состояний определяются уравнениями:

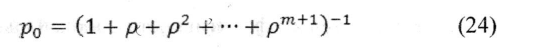
Отсюда получаем, что если р 1, то

Тогда остальные предельные вероятности находятся по формулам:

Постановка задачи
Параметры m , λ и μ известны.
Требуется найти

Формулы для расчетов
Приведенная интенсивность потока заявок вычисляется, как и в предыдущих параграфах, по формуле

Вероятности вычисляются по следующим формулам:

Поскольку заявка получает отказ, если СМО занята, а в очереди находятся m заявок, то

Далее получаем

Кроме того, справедливы формулы

Пример 10.
Автозаправочная станция (АЗС) представляет собой СМО с одним каналом обслуживания (одной колонкой).
Площадка при станции допускает пребывание в очереди на заправку не более пяти машин одновременно (m = 5). Об этом говорит сайт https://intellect.icu . Если
в очереди уже находятся пять машины, очередная машина, прибывшая к станции, в очередь не становится. Поток
машин, прибывающих для заправки, имеет интенсивность λ = 2 (машина в минуту). Интенсивность потока
обслуживания составляет μ = 2.

Определите характеристики СМО и сделайте вывод об эффективности ее работы.

Решение.

Среднее число находящихся в системе заявок:

Среднее время пребывания машины в системе:

Средняя длина очереди:
Среднее время ожидания в очереди: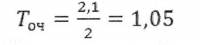

Каждому седьмому клиенту отказывают в обслуживании => эффективность СМО низкая.

Пример 11.
В небольшом магазине самообслуживания установлено, что поток покупателей является простейшим с интенсивностью λ = 1 покупатель в минуту. В этом магазине установлен один кассовый аппарат, позволяющий добиться такой производительности труда, при которой среднее время обслуживания одного клиента составляет примерно 1,25 мин. покупателя в минуту.

Определите характеристики СМО при условии, что очередь ограничена контролером при входе в зал самообслуживания: m = 3 покупателей.

Решение: Найдем интенсивность потока обслуживания:

Найдем приведенную интенсивность потока заявок:

Найдем предельные вероятности:

Вероятность отказа:

Относительная пропускная способность СМО:

Абсолютная пропускная способность СМО:

покупателей в мин.
Среднее число покупателей у кассы:

Среднее время пребывания покупателя у кассы:

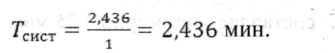
Среднее число покупателей в очереди:

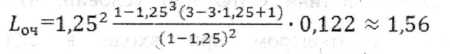
т.е. среднее число покупателей, ожидающих в очереди у кассы, равно 1,56.
Среднее время ожидания покупателя в очереди:

Вероятность простоя кассира мала, среднее время оживания покупателя не большое, вероятность отказа примерно 0,297. Таким образом, можно сказать, что система работает эффективно.

Задачи для самоконтроля

1. На автомойке один блок для обслуживания и есть место для очереди. Автомобили прибывают по пуассоновскому распределению с интенсивностью 5 авто/час. Среднее время обслуживания одной машины - 10 минут. Найдите все средние характеристики СМО.

Ответ

2. Автосервис (пост диагностики) представляет собой одноканальную СМО. Число стоянок для автомобилей, ожидающих обслуживания ограничено и равно 3. Если все стоянки заняты, то есть в очереди уже находятся три автомобиля, то очередной автомобиль, прибывший в автосервис на диагностику, в очередь на обслуживание не становится. Поток автомобилей, прибывающих на диагностику, распределен по показательному закону Пуассона и имеет интенсивность 0,85 (автомобиля в час). Время диагностики распределено по показательному закону и в среднем равно 1,05 час. Определите вероятностные характеристики работы СМО и сделайте вывод об эффективности ее работы.

Ответ:

Если я не полностью рассказал про расчет показателей эффективности одноканальной смо с ограниченной очередью? Напиши в комментариях Надеюсь, что теперь ты понял что такое расчет показателей эффективности одноканальной смо с ограниченной очередью, одноканальная смо с ограниченной очередью и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория массового обслуживания

Из статьи мы узнали кратко, но содержательно про расчет показателей эффективности одноканальной смо с ограниченной очередью