Привет, мой друг, тебе интересно узнать все про расчет показателей эффективности многоканальной смо с отказами, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое
расчет показателей эффективности многоканальной смо с отказами, многоканальная смо с отказами , настоятельно рекомендую прочитать все из категории Теория массового обслуживания.
-
Многоканальная система с отказами
Рассмотрим классическую задачу Эрланга.
Имеется n каналов, на которые поступает поток заявок с интенсивностью λ. Поток обслуживаний имеет интенсивность μ. Найти предельные вероятности состояний системы и показатели ее эффективности.
Система S (СМО) имеет следующие состояния (нумеруем их по числу заявок, находящихся в системе): S0, S1, S2, …, Sk, …, Sn, где Sk — состояние системы, когда в ней находится k заявок, т.е. занято k каналов.
Граф состояний СМОсоответствует процессу гибели и размножения и показан на рис. 7.
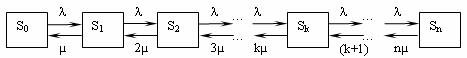
Рис. 7
Поток заявок последовательно переводит систему из любого левого состояния в соседнее правое с одной и той же интенсивностью λ. Интенсивность же потока обслуживаний, переводящих систему из любого правого состояния в соседнее левое состояние, постоянно меняется в зависимости от состояния. Действительно, если СМО находится в состоянии S2 (два канала заняты), то она может перейти в состояние. S1 (один канал занят), когда закончит обслуживание либо первый, либо второй канал, т.е. суммарная интенсивность их потоков обслуживании будет 2μ. Аналогично суммарный поток обслуживаний, переводящий СМО из состояния S3 (три канала заняты) в S2. Об этом говорит сайт https://intellect.icu . будет иметь интенсивность Зμ, т.е. может освободиться любой из трех каналов и т.д.
В формуле (16) для схемы гибели и размножения получим для предельной вероятности состояния
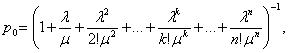 (23)
(23)
где члены разложения  будут представлять собой коэффициенты приp0 в выражениях для предельных вероятностей p1, p2, …, pk, …, pn. Величина
будут представлять собой коэффициенты приp0 в выражениях для предельных вероятностей p1, p2, …, pk, …, pn. Величина
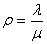 (24)
(24)
называется приведенной интенсивностью потока заявок или интенсивностью нагрузки канала.Она выражает среднее число заявок, приходящее за среднее время обслуживания одной заявки. Теперь
p1=ρ·p0 (25)
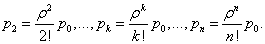 (26)
(26)
Формулы (25) и (26) для предельных вероятностей получили названия формул Эрланга в честь основателя теории массового обслуживания.
Вероятность отказа СМО есть предельная вероятность того, что все n каналов системы будут заняты, т.е.
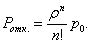 (27)
(27)
Относительная пропускная способность — вероятность того, что заявка будет обслужена:
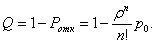 (28)
(28)
Абсолютная пропускная способность:
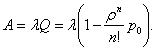 (29)
(29)
Среднее число занятых каналов k есть математическое ожидание числа занятых каналов:
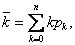
где pk — предельные вероятности состояний, определяемых по формулам (25), (26).
Однако среднее число занятых каналов можно найти проще, если учесть, что абсолютная пропускная способность системы А есть не что иное, как интенсивность потока обслуженных системой заявок (в единицу времени). Так как каждый занятый канал обслуживает в среднем μ заявок (в единицу времени), то среднее число занятых каналов
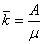 (30)
(30)
или, учитывая (29), (24):
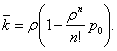 (31)
(31)
Вау!! 😲 Ты еще не читал? Это зря!
Если я не полностью рассказал про расчет показателей эффективности многоканальной смо с отказами? Напиши в комментариях Надеюсь, что теперь ты понял что такое расчет показателей эффективности многоканальной смо с отказами, многоканальная смо с отказами
и для чего все это нужно, а если не понял, или есть замечания,
то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Теория массового обслуживания
Из статьи мы узнали кратко, но содержательно про расчет показателей эффективности многоканальной смо с отказами
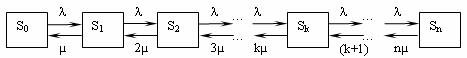
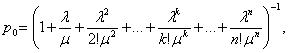 (23)
(23) будут представлять собой коэффициенты приp0 в выражениях для предельных вероятностей p1, p2, …, pk, …, pn. Величина
будут представлять собой коэффициенты приp0 в выражениях для предельных вероятностей p1, p2, …, pk, …, pn. Величина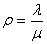 (24)
(24)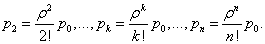 (26)
(26)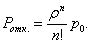 (27)
(27)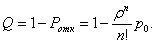 (28)
(28)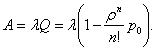 (29)
(29)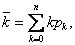
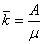 (30)
(30)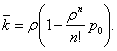 (31)
(31)
Комментарии
Оставить комментарий
Теория массового обслуживания
Термины: Теория массового обслуживания