19.7. Марковский случайный процесс кратко

Привет, Вы узнаете о том , что такое марковский случайный процесс, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое марковский случайный процесс , настоятельно рекомендую прочитать все из категории Теория массового обслуживания.

Допущения о пуассоновском характере потока заявок и о показательном распределении времени обслуживания ценны тем, что позволяют применить в теории массового обслуживания аппарат так называемых марковских случайных процессов.

Процесс, протекающий в физической системе, называется марковским (или процессом без последействия), если для каждого момента времени вероятность любого состояния системы в будущем зависит только от состояния системы в настоящий момент 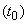 и не зависит от того, каким образом система пришла в это состояние.

Рассмотрим элементарный пример марковского случайного процесса. По оси абсцисс 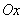 случайным образом перемещается точка 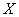. В момент времени  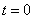точка 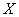 находится в начале координат  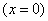и остается там в течение одной секунды. Через секунду бросается монета; если выпал герб - точка  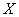перемещается на одну единицу длины вправо, если цифра - влево. Через секунду снова бросается монета и производится такое же случайное перемещение, и т. д. Процесс изменения положения точки (или, как говорят, «блуждания») представляет собой случайный процесс с дискретным временем  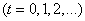и счетным множеством состояний

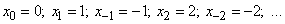
Схема возможных переходов для этого процесса показана на рис. 19.7.1.

Рис. 19.7.1.

Покажем, что этот процесс - марковский. Действительно, представим себе, что в какой-то момент времени 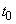 система находится, например, в состоянии  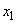- на одну единицу правее начала координат. Возможные положения точки через единицу времени будут  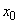и 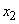 с вероятностями 1/2 и 1/2; через две единицы - 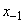, , 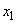 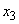с вероятностями 1/4, ½, 1/4 и так далее. Очевидно, все эти вероятности зависят только от того, где находится точка в данный момент 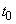, и совершенно не зависят от того, как она пришла туда.

Рассмотрим другой пример. Об этом говорит сайт https://intellect.icu . Имеется техническое устройство 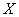, состоящее из элементов (деталей) типов  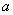и 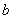, обладающих разной долговечностью. Эти элементы в случайные моменты времени и независимо друг от друга могут выходить из строя. Исправная работа каждого элемента безусловно необходима для работы устройства в целом. Время безотказной работы элемента - случайная величина, распределенная по показательному закону; для элементов типа  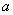и 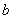 параметры этого закона различны и равны соответственно  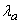и 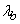. В случае отказа устройства немедленно принимаются меры для выявления причин и обнаруженный неисправный элемент немедленно заменяется новым. Время, потребное для восстановления (ремонта) устройства, распределено по показательному закону с параметром  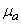(если вышел из строя элемент типа 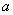) и 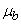(если вышел из строя элемент типа ).

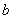В данном примере случайный процесс, протекающий в системе, есть марковский процесс с непрерывным временем и конечным множеством состояний:

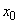 - все элементы исправны, система работает,

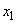 - неисправен элемент типа 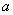, система ремонтируется,

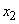 - неисправен элемент типа 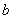, система ремонтируется.

Схема возможных переходов дана на рис. 19.7.2.

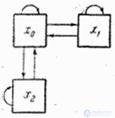
Рис. 19.7.2.

Действительно, процесс обладает марковским свойством. Пусть например, в момент 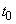 система находится в состоянии  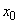(исправна). Так как время безотказной работы каждого элемента - показательное, то момент отказа каждого элемента в будущем не зависит от того, сколько времени он уже работал (когда поставлен). Поэтому вероятность того, что в будущем система останется в состоянии  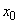или уйдет из него, не зависит от «предыстории» процесса. Предположим теперь, что в момент  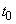система находится в состоянии  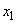(неисправен элемент типа 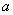). Так как время ремонта тоже показательное, вероятность окончания ремонта в любое время после  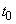не зависит от того, когда начался ремонт и когда были поставлены остальные (исправные) элементы. Таким образом, процесс является марковским.

Заметим, что показательное распределение времени работы элемента и показательное распределение времени ремонта - существенные условия, без которых процесс не был бы марковским. Действительно, предположим, что время исправной работы элемента распределено не по показательному закону, а по какому-нибудь другому - например, по закону равномерной плотности на участке 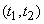. Это значит, что каждый элемент с гарантией работает время 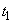, а на участке от  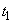до 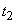 может выйти из строя в любой момент с одинаковой плотностью вероятности. Предположим, что в какой-то момент времени  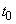элемент работает исправно. Очевидно, вероятность того, что элемент выйдет из строя на каком-то участке времени в будущем, зависит от того, насколько давно поставлен элемент, т. е. зависит от предыстории, и процесс не будет марковским.

Аналогично обстоит дело и с временем ремонта 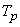; если оно не показательное и элемент в момент  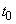ремонтируется, то оставшееся время ремонта зависит от того, когда он начался; процесс снова не будет марковским.

Вообще показательное распределение играет особую роль в теории марковских случайных процессов с непрерывным временем. Легко убедиться, что в стационарном марковском процессе время, в течение которого система остается в каком-либо состоянии, распределено всегда по показательному закону (с параметром, зависящим, вообще говоря, от этого состояния). Действительно, предположим, что в момент 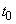 система находится в состоянии  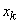и до этого уже находилась в нем какое-то время. Согласно определению марковского процесса, вероятность любого события в будущем не зависит от предыстории; в частности, вероятность того, что система уйдет из состояния  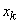в течение времени 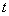, не должна зависеть от того, сколько времени система уже провела в этом состоянии. Следовательно, время пребывания системы в состоянии  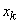должно быть распределено по показательному закону.

В случае, когда процесс, протекающий в физической системе со счетным множеством состояний и непрерывным временем, является марковским, можно описать этот процесс с помощью обыкновенных дифференциальных уравнений, в которых неизвестными функциями являются вероятности состояний 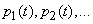. Составление и решение таких уравнений мы продемонстрируем в следующем  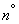на примере простейшей системы массового обслуживания.

Информация, изложенная в данной статье про марковский случайный процесс , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое марковский случайный процесс и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория массового обслуживания