Многоканальная СМО с неограниченной очередью

Привет, Вы узнаете о том , что такое многоканальная смо с неограниченной очередью , Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое многоканальная смо с неограниченной очередью , настоятельно рекомендую прочитать все из категории Теория массового обслуживания.

Рассмотрим n-канальную систему массового обслуживания неограниченной очередью, в которую поступает простейший поток заявок с интенсивностью λ;
интенсивность обслуживания μ (т.е. в среднем непрерывно занятый канал будет выдавать ρ = λ/ μ обслуженных заявок в единицу (времени).
Длительность обслуживания - случайная величина, подчиненная показательному закону распределения.

Поток обслуживания является простейшим пуассоновским потоком событий.
Заявка, поступившая в момент, когда все п каналов заняты, становится в очередь и ожидает обслуживания.
В качестве показателей эффективности одноканальной СМО с ограниченной длиной очереди будем рассматривать:

А - абсолютную пропускную способность СМО;
Q - относительную пропускную способность;
Ротк - вероятность отказа;
Роч - вероятность образования очереди;
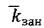- среднее число занятых каналов;
L_сист - среднее число находящихся в системе заявок;
Т_сист — среднее время пребывания заявки в системе;
Lоч - средняя длина очереди;
Точ- среднее время ожидания в очереди.
Размеченный граф состояний представлен на рисунке 12.

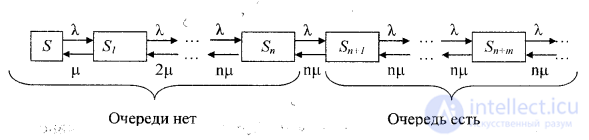
Рис . 12. Многоканальна я СМ О с ограниченной длинной очереди

S0 - все каналы свободны, к = 0;
S1 - занят один канал, остальные свободны, к = 1 ;

***
S„ - заняты все п каналов, очереди нет, к = п;
S„+i - заняты все п каналов, одна заявка в очереди к = п + 1 ;

***

Sn+m-заняты все п каналов, г заявок в очереди, к=п + т;

Поскольку ограничение на длину очереди отсутствует, то любая заявка может быть обслужена, поэтому Робс= 1,
следовательно, относительная пропускная способность 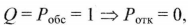a абсолютная проп}'скная способность

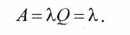
Предельные вероятности:

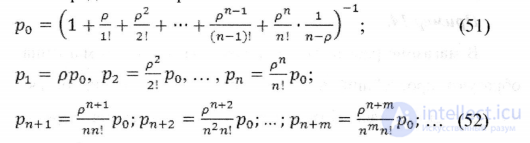
Вероятность образования очереди;

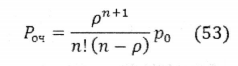
Среднее число занятых каналов:

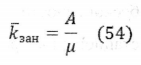
Средняя длина очереди:

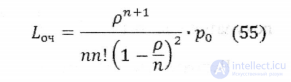
Среднее время ожидания в очереди:

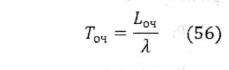
Среднее число заявок в системе:

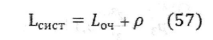
Среднее время пребывания заявки в СМО:

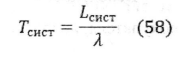
Если p < п, то процесс обслуживания устойчив.

Если р > п => СМО работает неустойчиво.

Пример

В магазине работают 3 продавца. Покупатели магазина образуют простейший поток требований с интенсивностью 90 человек в час. Интенсивность обслуживания одного покупателя составляет 60 человек в час.

Найдите характеристики обслуживания.

Решение

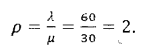
По условию р < п, следовательно, очередь не будет возрастать до бесконечности и в системе наступает предельный стационарный режим работы.
Найдем вероятность того, что у касс отсутствуют покупатели:

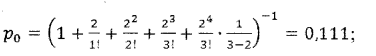
Вероятность того, что у касс обслуживаются один, два, три покупателя, находим по формулам:

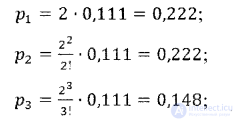
Вероятность того, что у касс стоят в очередь один, два покупателя, находим по формулам:

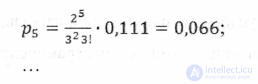
Вероятность того, что заявка окажется в очереди, определяется по формуле

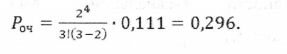
Среднее число занятых касс: 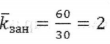кассира.
Среднее число покупателей в очереди:

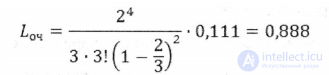
Среднее число покупателей, обслуживаемых кассирами и стоящих в очереди:
L_сист = 0.883 + 2 = 2,888

Среднее время пребывания заявки в очереди:

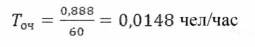
Среднее время пребывания заявки в системе:

Вопросы для самоконтроля

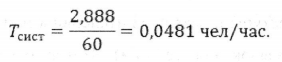
1. Об этом говорит сайт https://intellect.icu . Чему равно число состояний n-канальной СМО с неограниченным ожиданием?
2. Нарисуйте размеченный граф состояний для гаканальной СМО с неограниченным ожиданием.
3. Сформулируйте условие существования финальных вероятностей для n-канальной СМО с неограниченным ожиданием.
4. Чему равны абсолютная и относительная пропускные - способности n-канальной СМО с неограниченным ожиданием?
5. С какими характеристиками эффективности пканальной СМО с ожиданием совпадает среднее число занятых каналов данной системы?
6. Как связаны между собой временные характеристики «среднее время обслуживания одной заявки, относящееся ко всем заявкам» и «среднее время обслуживания одной заявки, относящееся только к обслуженным заявкам» для гск^чальной СМО с неограниченным ожиданием?

Задачи для самоконтроля

1. В многоканальную СМО с двумя каналами обслуживания поступают заявки с интенсивностью 0,8 заявок в час. (Поток заявок простейший). Поток обслуживания имеет интенсивность 0,5 заявки в час. Очередь заявок на обслуживание может расти практически неограниченно.
Определите все средние характеристики системы.

Ответ:

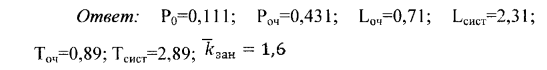
2. В морском порту три причала, интенсивность входного потока - 2,5 судов в сутки. Интенсивность погрузочно-разгрузочных работ - 2 судна в день. Поток
заявок и поток обслуживания пуассоновские. Очередь судов может расти практически неограниченно. Имея в виду стационарный режим работы, определить все средние характеристики системы.

Ответ:

Задачи для самостоятельного решения

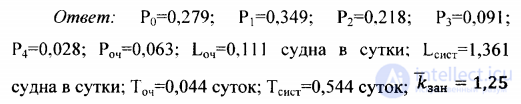
1. Автозаправочная станция имеет 4 бензоколонки. Среднее время заправки 2 мин. Входящий поток автомашин - простейший с интенсивностью 1,5 авт./мин. При всех занятых колонках требование теряется. Определите вероятность отказа и среднее число занятых колонок.

2. Покупатели магазина образуют простейший поток требований с интенсивностью 150 чел/ч. Определите наименьшее число продавцов, при которых среднее число покупателей, ожидающих обслуживания, не превысит 3.

3. В нефтеналивном порту 4 причала для заправки танкеров, которые приходят в среднем через 18 ч, а время загрузки составляет в среднем двое суток. В очереди могут стоять не более 2 танкеров. Определите пропускную способность и холостой ход порта.

4. Определите закон распределения промежутка времени между приходом двух требований в простейшем потоке требований интенсивностью L

5. Поток желающих оформить вызов врача на дом - простейший. В среднем абоненты звонят через каждые 10 с. Время приема вызова распределено по показательному закону со средним значением 12 с. Определите наименьшее число телефонов в регистратуре, при котором вызов принимается не менее чем от 90% абонентов. Считается, что в случае неудачи абонент не предпринимает больше попыток дозвониться.

6. Докажите, что выходящий из показательного канала (на входе которого всегда имеются заявки) поток является простейшим.

7. Автоматическая мойка может принять на обслуживание одновременно 4 автомашины. В среднем машины прибывают через 2 мин, а средняя продолжительность мойки - 10 мин. В очереди могут находиться не более 6 машин. Определите вероятность того, что в системе находится хотя бы одна машина, и загруженность одной установки для мойки машин.

8. В магазине имеется 3 справочных телефона. В среднем обращаются за справками 40 чел/ч. Средняя продолжительность справочного разговора 3 мин. Издержки, связанные с работой одного телефона, - а руб./мин. Определите минимальную стоимость одной минуты разговора по телефону, при которой система неубыточна.

9. Платная стоянка для легковых машин имеет 7 мест. Найдите вероятность того, что прибывшая машина найдет свободное место, если машины в среднем
прибывают через 10 мин. а занимают место на стоянке всреднем 1ч.

10. Поток деталей, сходящих с конвейера, простейший с интенсивностью 2 дет/мин. Время проверки детали контролером имеет показательный закон распределения со средним 2 мин/дет. Определите долю непроверенных деталей.

11. Город обслуживают 4 машины скорой помощи. Вызовы поступают в среднем через 4 ч. Вероятность того, что хотя бы одна машина занята, равна 0,25. Определите среднее число занятых машин и среднюю долю простоя машин.

12. В парикмахерской работают два мастера. Время обслуживания распределено по показательному закону сосредним 12 мин. Ожидать обслуживание могут не более трех человек. Поток клиентов - простейший с интенсивностью 10 клиентов/ч. Найдите важнейшие операционные характеристики этой системы.
к.

13. Система автоматической посадки самолетов одновременно может хранить данные только о шести самолетах, находящихся в воздухе. Самолеты, подлетающие к аэродрому, образуют простейший поток с интенсивностью 6 самолетов/ч. Если в момент запроса посадки система заполнена, то самолет улетает к запасному аэродрому. Аэродром имеет 3 посадочные полосы, самолет занимает полосу в среднем 20 мин. Найдите пропускную способность СМО, загруженность одной полосы, среднее число занятых полос, среднее время ожидания начала посадки после запроса.

14. Рассматривается работа автозаправочной станции (АЗС), на которой имеется 2 заправочные колонки. Предположим, что она описывается процессом размножения и гибели в стационарном режиме. Заправка каждой машины длится в среднем 3 минуты. В среднем на АЗС каждые две минуты прибывает машина, нуждающаяся в заправке. Число мест в очереди неограниченно. Все машины, вставшие на заправку, терпеливо дожидаются своей очереди. Определите: 1. Вероятность того, что на заправке находится 5 машин. 2. Вероятность того, что вновь прибывшей машине придется ждать обслуживания.

15. Закусочная на АЗС имеет один прилавок. Автомобили прибывают в соответствии с пуассоновским распределением, в среднем 2 автомобиля за 5 минут. Для выполнения заказа в среднем достаточно 1.5 минуты, хотя продолжительность обслуживания распределена по экспоненциальному закону. Найдите: а) вероятность простояприлавка; b) средние характеристики; с) вероятность того, что количество прибывших автомобилей будет не менее 10.

16. Рентгеновский аппарат позволяет обследовать в среднем 7 человек в час. Интенсивность посетителей составляет 5 человек в час. Предполагая стационарный режим работы, определите средние характеристики.

17. В речном порту один причал, интенсивность входного потока - 5 судов в день. Интенсивность погрузочно-разгрузочных работ - 6 судов в день. Имея в
виду стационарный режим работы, определите все средние характеристики системы.

18. Какое оптимальное число каналов обслуживания должна иметь СМО, если интенсивность потока заявок равна 3, среднее число, заявок обслуженных в единицу времени равно 2, штраф за каждый отказ равен 5, а стоимость простоя одной линии равна 2?

19. Какое оптимальное число каналов обслуживания должна иметь СМО, если интенсивность потока заявок равна 3, среднее число, заявок обслуженных в единицу
времени равно 1, штраф за каждый отказ равен 7, а стоимость простоя одной линии равна 3?

20. Какое оптимальное число каналов обслуживания должна иметь СМО, если интенсивность потока заявок равна 4, среднее число, заявок обслуженных в единицу времени равно 2, штраф за каждый отказ равен 5, а стоимость простоя одной линии равна 1 ?

21. Определите число взлетно-посадочных полос для самолетов с учетом требования, что вероятность ожидания должна быть меньше, чем 0.05. При этом интенсивность входного потока 27 самолетов в сутки, а интенсивность их обслуживания - 30 самолетов в сутки.

22. Сколько равноценных независимых конвейерных линий должен иметь цех, чтобы обеспечить ритм работы, при котором вероятность ожидания обработки изделий должна быть меньше 0.03 (каждое изделие выпускается одной линией). Известно, что интенсивность поступления заказов 30 изделий в час, а интенсивность обработки изделия одной линией - 36 изделий в час.

23. Среднее число вызовов, поступающих на АТС за одну минуту, равно 3. Считая поток пуассоновским, найдите вероятность того, что за 2 минуты поступит: а) два вызова; б) меньше двух вызовов; в) не менее двух вызовов.

24. Сколько каналов должна иметь СМО с отказами, если интенсивность потока заявок равна 2треб/час, среднее число, заявок обслуженных в единицу времени равно 1 треб/час, штраф за каждый отказ составляет 8т.руб., стоимость простоя одной линии - 2т.руб. в час?

25. Система массового обслуживания представляет собой автоматическую телефонную станцию, которая может обеспечить не более пяти переговоров одновременно. Заявкавызов, поступившая в тот момент, когда все каналы заняты, получает отказ и покидает систему. В среднем на станцию
поступает 0,8 вызовов в минуту, а средняя продолжительность одних переговоров равна 1,5 минуты. Для стационарного режима функционирования системы необходимо определите: а) вероятности состояний системы; б) вероятность отказа; в) абсолютную и относительную пропускные способности; г) среднее число занятых каналов.

26. Автозаправочная станция имеет одну бензоколонку с площадкой, допускающей пребывание в очереди на заправку не более трех автомашин одновременно.
Если в очереди на заправку уже находятся три автомашины, то очередная автомашина, прибывшая на станцию, проезжаетмимо. В среднем на заправку прибывает одна машина в минуту, а сам процесс заправки в среднем длится 1,25 минуты. Для стационарного режима функционирования автозаправочной станции необходимо определите: а) вероятность отказа; б) относительную и абсолютную пропускные способности; в) среднее число автомашин в очереди на заправку; г) среднее время ожидания в очереди.

Вау!! 😲 Ты еще не читал? Это зря!

• одноканальная смо с неограниченной очередью

Исследование, описанное в статье про многоканальная смо с неограниченной очередью , подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое многоканальная смо с неограниченной очередью и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория массового обслуживания

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.