19.5. Поток с ограниченным последействием (поток Пальма) кратко

Привет, Вы узнаете о том , что такое поток с ограниченным последействием поток пальма , Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое поток с ограниченным последействием поток пальма , настоятельно рекомендую прочитать все из категории Теория массового обслуживания.

В предыдущем 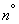мы познакомились с естественным обобщением простейшего потока - с нестационарным пуассоновским потоком. Обобщением простейшего потока в другом направлении является поток с ограниченным последействием.

 

Рассмотрим ординарный поток однородных событий (рис. 19.5.1).

Рис. 19.5.1.

Этот поток называется потоком с ограниченным последействием (или потоком Пальма), если промежутки времени между последовательными событиями 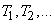 представляют собой независимые случайные величины.

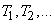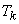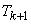Очевидно, простейший поток является частным случаем потока Пальма: в нем расстояния  представляют собой независимые случайные величины, распределенные по показательному закону. Что касается нестационарного пуассоновского потока, то он не является потоком Пальма. Действительно, рассмотрим два соседних промежутка  и  в нестационарном пуассоновском потоке. Как мы видели в предыдущем 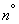, закон распределения промежутка между событиями в нестационарном потоке зависит от того, где этот промежуток начинается, а начало промежутка  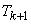совпадает с концом промежутка 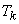; значит, длины этих промежутков зависимы.

Рассмотрим примеры потоков Пальма.

1. Некоторая деталь технического устройства (например, радиолампа) работает непрерывно до своего отказа (выхода из строя), после чего она мгновенно заменяется новой. Срок безотказной работы детали случаен; отдельные экземпляры выходят из строя независимо друг от друга. При этих условиях поток отказов (или поток «восстановлений») представляет собой поток Пальма. Если, к тому же, срок работы детали распределен по показательному закону, то поток Пальма превращается в простейший.

2. Группа самолетов идет в боевом порядке «колонна» (рис. 19.5.2) с одинаковой для всех самолетов скоростью 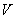. Каждый самолет, кроме ведущего, обязан выдерживать строй, т. е. держаться на заданном расстоянии  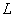от впереди идущего. Это расстояние, вследствие погрешностей радиодальномера, выдерживается с ошибками. Моменты пересечения самолетами заданного рубежа образуют поток Пальма, так как случайные величины 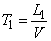; ; 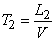… независимы. Заметим, что тот же поток не будет потоком Пальма, если каждый из самолетов стремится выдержать заданное расстояние не от соседа, а от ведущего.

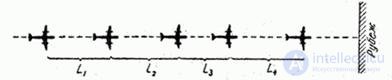
Рис. 19.5.2.

Потоки Пальма часто получаются в виде выходных потоков систем массового обслуживания. Если на какую-либо систему поступает какой-то поток заявок, то он этой системой разделяется на два: поток обслуженных и поток необслуженных заявок.

Поток необслуженных заявок часто поступает на какую-либо другую систему массового обслуживания, поэтому представляет интерес изучить его свойства.

Основной в теории выходных потоков является теорема Пальма, которую мы сформулируем без доказательства.

Пусть на систему массового обслуживания поступает поток заявок типа Пальма, причем заявка, заставшая все каналы занятыми, получает отказ (не обслуживается). Если при этом время обслуживания имеет показательный закон распределения, то поток необслуженных заявок является также потоком типа Пальма.

В частности, если входной поток заявок будет простейшим, то поток необслуженных заявок, не будучи простейшим, будет все же иметь ограниченное последействие.

Интересным примером потоков с ограниченным последействием являются так называемые потоки Эрланга. Они образуются «просеиванием» простейшего потока.

Рассмотрим простейший поток (рис. 19.5.3) и выбросим из него каждую вторую точку (на рисунке выброшенные точки отмечены крестами).

Рис. 19.5.3.

Оставшиеся точки образуют поток; этот поток называется потоком Эрланга первого порядка 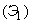. Очевидно, этот поток есть поток Пальма: поскольку независимы промежутки между событиями в простейшем потоке, то, независимы и величины 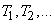, получающиеся суммированием таких промежутков по два.

Поток Эрланга второго порядка получится, если сохранить в простейшем потоке каждую третью точку, а две промежуточные выбросить (рис. 19.5.4).

Рис. 19.5.4.

Вообще, потоком Эрланга k-го порядка 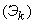 называется поток, получаемый из простейшего, если сохранить каждую 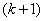-ю точку, а остальные выбросить. Об этом говорит сайт https://intellect.icu . Очевидно, простейший поток можно рассматривать как поток Эрланга нулевого порядка .

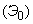Найдем закон распределения промежутка времени 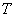 между соседними событиями в потоке Эрланга 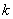-го порядка 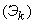. Рассмотрим на оси  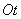(рис. 19.5.5) простейший поток с интервалами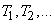  

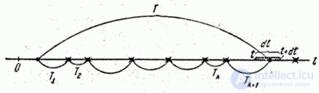
Рис. 19.5.5.

Величина 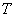 представляет собой сумму  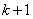независимых случайных величин

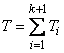,                  (19.5.1)

где 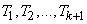 - независимые случайные величины, подчиненные одному и тому же показательному закону

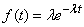
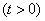   .           (19.5.2)

Можно было бы найти закон распределения величины 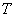 как композицию  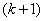законов (19.5.2). Однако проще вывести его элементарными рассуждениями.

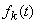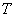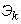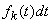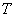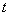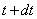Обозначим  плотность распределения величины  для потока ;  есть вероятность того, что величина  примет значение между  и  (рис. 19.5.5). Это значит, что последняя точка промежутка  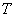должна попасть на элементарный участок 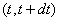, а предыдущие  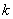точек простейшего потока - на участок 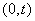. Вероятность первого события равна  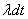вероятность второго, на основании формулы (19.3.2), будет

.

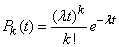Перемножая эти вероятности, получим

,

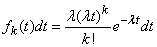откуда

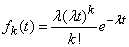
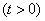   .                       (19.5.3)

Закон распределения с плотностью (19.5.3) называется законом Эрланга 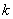-го порядка. Очевидно, при  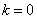он обращается в показательный

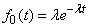
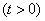 .           (19.5.4)

Найдем характеристики закона Эрланга 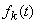: математическое ожидание  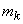и дисперсию 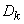. По теореме сложения математических ожиданий

,

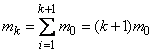где 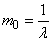 - математическое ожидание промежутка между событиями в простейшем потоке.

Отсюда

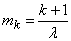.                            (19.5.5)

Аналогично по теореме сложения дисперсий

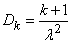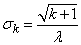,  .                 (19.5.6)

Плотность 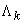 потока  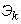будет обратна величине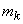 

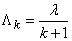.                (19.5.7)

Таким образом, при увеличении порядка потока Эрланга увеличиваются как математическое ожидание, так и дисперсия промежутка времени между событиями, а плотность потока падает.

Выясним, как будет изменяться поток Эрланга при 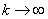, если его плотность будет сохраняться постоянной? Пронормируем величину  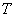так, чтобы ее математическое ожидание (и, следовательно, плотность потока) оставалось неизменным. Для этого изменим масштаб по оси времени и вместо  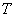рассмотрим величину

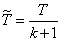.                   (19.5.8)

Назовем такой поток нормированным потоком Эрланга 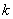-го порядка. Закон распределения промежутка  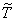между событиями этого потока будет

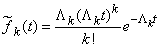
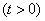                   ,                       (19.5.9)

где 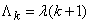, или

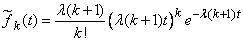
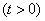          .           (19.5.10)

Математическое ожидание величины 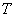, распределенной по закону (19.5.10), не зависит от  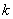и равно

,

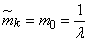где 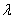 - плотность потока, совпадающая при любом  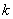с плотностью исходного простейшего потока. Дисперсия величины  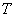равна

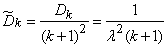                 (19.5.11)

и неограниченно убывает с возрастанием .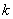

Таким образом, мы приходим к выводу: при неограниченном увеличении 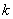 нормированный поток Эрланга приближается к регулярному потоку с постоянными интервалами, равными .

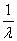Это свойство потоков Эрланга удобно в практических применениях: оно дает возможность, задаваясь различными 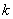, получить любую степень последействия: от полного отсутствия  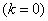до жесткой функциональной связи между моментами появления событий 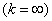. Таким образом, порядок потока Эрланга может служить как бы «мерой последействия», имеющегося в потоке. В целях упрощения часто бывает удобно заменить реальный поток заявок, имеющий последействие, нормированным потоком Эрланга с примерно теми же характеристиками промежутка между заявками: математическим ожиданием и дисперсией.

Пример. В результате статистической обработки промежутков между заявками в потоке получены оценки для математического ожидания и дисперсии величины :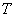

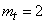(мин),  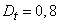(мин2).

Заменить этот поток нормированным потоком Эрланга с теми же характеристиками.

Решение. Имеем

.

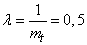Из формулы (19.5.11) получим

,                     .

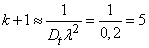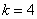Поток можно приближенно заменить нормированным потоком Эрланга четвертого порядка.

 

Информация, изложенная в данной статье про поток с ограниченным последействием поток пальма , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое поток с ограниченным последействием поток пальма и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория массового обслуживания

Из статьи мы узнали кратко, но содержательно про поток с ограниченным последействием поток пальма