7: Способы представления чисел в компьютере, Арифметические действия над числами с плавающей точкой

Привет, Вы узнаете о том , что такое способы представления чисел в эвм, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое способы представления чисел в эвм , настоятельно рекомендую прочитать все из категории Цифровые устройства. Микропроцессоры и микроконтроллеры. принципы работы ЭВМ.

Способ представления чисел сильно влияет на характер программирования. Так, программирование для компьютеров, работающих в системе с фиксированной запятой, значительно усложняется, поскольку помимо алгоритмических трудностей этот процесс требует еще отслеживания положения запятой.

Формы представления чисел в компьютере

Представление целых чисел числа

• с фиксированной точкой
• символьный способ представления
• двоично-десятичный способ

Представление вещественных чисел

• числа с фиксированной точкой
• числа с плавающей точкой

3. Основные понятия в представлении чисел с плавающей точкой.

3.1 Представление числа в нормализованном экспоненциальном виде.

Возьмем, к примеру, десятичное число 155,625
Представим это число в нормализованном экспоненциальном виде : 1,55625∙10⁺²=1,55625∙exp₁₀⁺²
Число 1,55625∙exp₁₀⁺² состоит из двух частей: мантиссы M=1.55625 и экспоненты exp₁₀=+2
Если мантисса находится в диапазоне 1<=M<10, то число считается нормализованным.
Экспонента представлена основанием системы исчисления (в данном случае 10) и порядком (в данном случае +2).
Порядок экспоненты может иметь отрицательное значение, например число 0,0155625=1,55625∙exp₁₀^-2.

3.2 Представление числа в денормализованном экспоненциальном виде.

Возьмем, к примеру, десятичное число 155,625
Представим это число в денормализованном экспоненциальном виде : 0,155625∙10⁺³=0,155625∙exp₁₀⁺³
Число 0,155625∙exp₁₀⁺³ состоит из двух частей: мантиссы M=0,155625 и экспоненты exp₁₀=+3
Если мантисса находится в диапазоне 0,1<=M<1, то число считается денормализованным.
Экспонента представлена основанием системы исчисления (в данном случае 10) и порядком (в данном случае +3).
Порядок экспоненты может иметь отрицательное значение, например число 0,0155625=0,155625∙exp₁₀^-3.

3.3 Преобразование десятичного числа в двоичное число с плавающей точкой.

Наша задача сводится к представлению десятичного числа с плавающей точкой, в двоичное число с плавающей точкой в экспоненциальном нормализованном виде. Для этого разложим заданное число по двоичным разрядам:

155,625 = 1∙2⁷ +0∙2⁶+0∙2⁵+1∙2⁴+1∙2³+0∙2²+1∙2¹+1∙2⁰+1∙2^-1+0∙2^-2+1∙2^-3
155,625 =128 + 0 + 0 + 16 + 8 + 0 + 2 + 1 + 0,5 + 0 + 0,125
155,625₁₀ = 10011011,101₂ - число в десятичной и в двоичной системе с плавающей точкой

Приведем полученное число к нормализованному виду в десятичной и двоичной системе:
1,55625∙exp₁₀⁺² = 1,0011011101∙exp₂⁺¹¹¹

В результате мы получили основные составляющие экспоненциального нормализованного двоичного числа:
Мантиссу M=1,0011011101
Экспоненту exp₂= +111

1. Представление целых чисел

1.1 Числа с фиксированной точкой

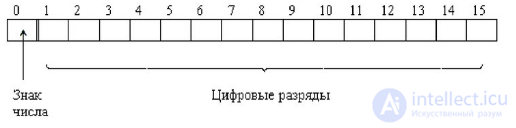
Диапазон представляемых чисел

• n разрядов:
• n=8 –128 .. 127
• n=16 –32 768 .. 32 767

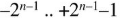
Диапазон беззнаковых чисел

Исключительная ситуация
FixedOverflow – переполнение с фиксированной запятой – результат операции превышает максимально возможное для данной разрядной сетки значение

• устанавливается в "1" флаг переполнения
• старший бит результата теряется
• в качестве результата выдается искаженное число.
• ситуация не считается критической, и после окончания данной операции вычисления продолжаются.

1.2. Символьный способ представления
число 397 = Код 3 Код 9 Код 7

1.3. Двоично-десятичный код
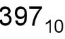= 0011 1001 0111

2. Представление вещественных чисел

2.1. Вещественные числа с фиксированной точкой

Достоинства

• простота
• выполнения арифметических операций
• высокая точность изображения чисел.

Недостаток

• небольшой диапазон представления чисел

2.2. Вещественные числа с плавающей точкой
Форма записи числа:

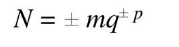
где
q – основание системы счисления,
p – порядок числа,
m – мантисса числа N.
Пример.

Нормализованная форма записи числа:
1/q ≤ | m | < 1.

а) представление чисел в формате полуслова

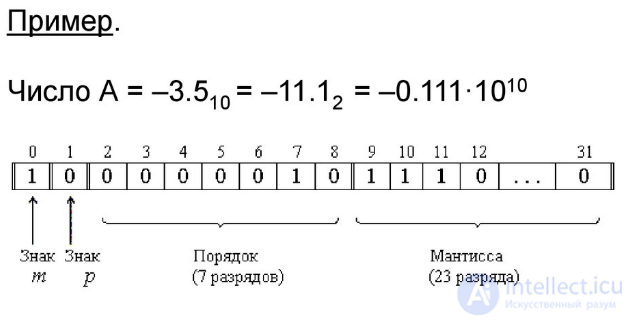
б) представление чисел в формате слова

Диапазон чисел определяется главным образом разрядностью порядка, а точность числа – только разрядностью мантиссы.
Таким образом, числа с плавающей точкой позволяют увеличить диапазон обрабатываемых чисел, но при этом точность изображения чисел
уменьшается по сравнению с числами с фиксированной точкой.

Пример.
Пусть имеем число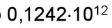в 10 с/с.
Мантисса имеет 4 разряда.
Тогда ближайшее большее этого числа равно .
Абсолютная погрешность

Ошибки и исключительные ситуации

1. Overflow - переполнение с плавающей запятой - в результате операции возникает число, имеющее порядок с большей разрядностью, чем допустимая при представлении порядка в машине

2. Появление машинных нулей, т.е. нормализованных чисел, отличных от нуля, но имеющих порядок, меньший самого малого порядка, представимого в разрядной сетке аппаратное прерывание работы выполнение программы после этого продолжается

3. Ошибка метода представления чисел - количество разрядов мантиссы больше количества, выделенного для ее представления в разрядной сетке ЭВМ, избыточные младшие разряды отбрасываются

Фиксированная точка(запятая)

разрядная сетка машины имеет постоянное число разрядов - n.

При представлении чисел с фиксированной точкой считают, что точка всегда находится перед старшим разрядом, а все числа, которые участвуют в вычислениях, считаются по абсолютной величине меньше единицы:

|X| < 1

Определим два понятия

Диапазон изменения характеризуется теми пределами, в которых могут находиться числа, с которыми оперирует машина.

Отличное от нуля самое малое число:

Таким образом, диапазон чисел, с которыми работает компьютер, есть:

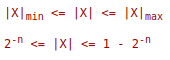
То есть, числа, которые выходят за диапазон изменения, в компьютере не могут быть представлены точно.

Если 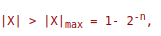то такое число воспринимается как бесконечно большое.

Этим двум случаям соответствуют понятия машинного нуля и машинной бесконечности.

При оптимальном округлении абсолютная ошибка:

Минимальная относительная ошибка:

так как при большом " n "

Максимальная относительная ошибка:

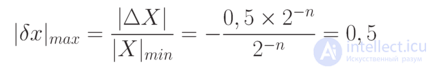
Ошибка представления числа зависит от величины самого числа и способа округления:

Заметим, что для малых чисел ошибка может достигать большой величины.

Плавающая запятая

В ЭВМ с плавающей запятой число представляется в виде:

Разрядная сетка машины принимает следующий вид:

Это лишь условное изображение основных слогов в числе. Заметим, что в реальной ЭВМ может быть принят любой другой порядок расположения.

Пусть " m " разрядов отведено под изображение мантиссы, а " k " разрядов под изображение порядка. Тогда для двоичной системы и нормализованного вида числа:

q = 2;

0,1 <= Mx < 1 - нормализованная мантисса.

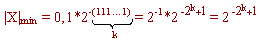
То есть диапазон чисел:

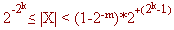
Абсолютная ошибка представления числа в компьютере с плавающей запятой равна:

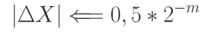
Видно, что относительная ошибка в компьютере с плавающей запятой не зависит от порядка числа.

При этом точность представления больших и малых чисел изменяется незначительно.

Теоретически " плавающая запятая " имеет преимущества перед " фиксированной ". Но соответствующее устройство получается намного сложнее. К тому же специфика выполнения операций с плавающей запятой требует большего числа микроопераций, что приводит к снижению быстродействия ЭВМ. Однако " плавающая запятая " снимает с программиста обязанность отслеживать положение запятой в вычислениях и значительно упрощает сам процесс программирования вычислительных задач.

Выполнение арифметических операций над числами, представленными с фиксированной запятой.

Основной особенностью различных методов выполнения арифметических операций является то, что любая операция (сложение, вычитание,умножение, деление и др.) сводится к некоторой последовательности микроопераций, таких как:

• сложение
• сдвиг
• передача
• преобразование кодов.

Микрооперация сложение

Сложение выполняется по правилам сложения чисел в позиционных системах счисления.

То есть эта операция выполняется поразрядно, а возникающий в младших разрядах перенос направляется в старшие разряды.

Пример:

Операции сложения производятся одновременно над всеми разрядами двух слагаемых и продолжаются до тех пор, пока возникают переносы. Возникающие переносы приводят к продолжению операции. Это одна из особенностей позиционных систем. Видим, что собственно операция определения частичной суммы слагаемых выполняется в один прием, а возникающие переносы распространяются на все более старшие разряды.

Микрооперация Сдвиг

Различают два вида микрооперации сдвига:

• логический сдвиг;
• арифметический сдвиг;

Логический сдвиг приводит к смещению всех разрядов числа, включая и знак, влево или вправо.

При этом освобождающиеся разряды заполняются нулями или единицами.

Арифметический сдвиг выполняется над частью числа, часть сдвинутых разрядов теряется. (Очевидно, знаковый разряд должен исключаться из рассмотрения).

Микрооперация Передача.

Эта микрооперация предполагает, что некоторый код (число) записывается в соответствующее устройство и вытесняет тот код, который там находился до передачи.

Различают два вида передач:

• запись (с разрушением ранее записанной информации);
• чтение (без разрушения).

Микрооперация Преобразование.

Функция, выполняемая над передаваемыми числами, называется преобразованием. Чаще других в арифметических основах рассматривают инвертирование кода. Это поразрядная микрооперация 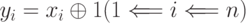, которая выполняется над всеми разрядами одновременно.

Коды, применяемые для изображения отрицательных чисел.

Основное неудобство построения устройств, реализующих арифметические операции, состоит в сложном характере алгоритма вычитания. Для его преодоления в ЭВМ всегда операция выполняется по иным правилам, чем это делается обычно. В его основе лежит операция сложения. Алгоритмы выполнения такого рода операций требуют специальных кодов представления отрицательных чисел.

Прямой код.

Это естественное и наиболее привычное представление числа в следующем виде:

знак:

" + " соответствует 0

" - " соответствует 1

В цифровых разрядах пишется модуль положительного или отрицательного числа.

[X]пк - обозначим таким образом изображение числа " X " в прямом коде.

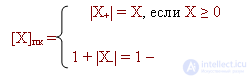
Рассмотрим диапазоны представляемых чисел:

Таким образом, нуль имеет двоякое изображение.

Замечания:

1. перед выполнением операции вычитания чисел с одинаковыми знаками и сложения с разными, необходимо сравнить по модулю два кода и, если нужно, сделать перестановку кодов местами, затем можно выполнять собственно операцию вычитания кодов.
2. при выполнении операции умножения отдельно и независимо находятся модули произведений кодов, а знак находится как результат операции сложения по модулю два:
   Собственно умножение выполняется с применением микроопераций сложения и сдвига.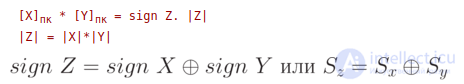
3. аналогично умножению выполняется операция деления с использованием микроопераций вычитания и сдвига.

Вследствие ряда неудобств в ЭВМ операции вычитания, сложения чисел с разными знаками и деления в прямом коде практически не выполняются.

Дополнительный код

Дополнительным называется код, в котором для положительного числа в знаковом разряде пишется "0", в цифровых - модуль числа, а для отрицательного в знаковом разряде пишется "1", в цифровых - дополнение числа до единицы.

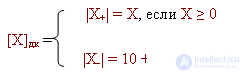
Если некоторое X- = -0,x1x2...xn нужно представить в дополнительном коде, то

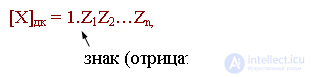
где: 1 - 0,x1x2...xn = 0, Z1Z2...Zn

Диапазоны представленных чисел:

Таким образом, нуль имеет единственное представление.

В самом деле, так как 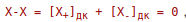, то в дополнительном коде: , если в разрядной сетке ЭВМ нет второго знакового разряда, то это переполнение теряется, и в знаковом разряде будет только нуль.

Важная особенность в получении дополнительного кода отрицательного числа состоит в следующем:

Таким образом, для записи дополнительного кода отрицательного числа необходимо в знаковом разряде поставить единицу, проинвертировать все цифровые разряды числа и прибавить единицу в младший разряд. Это также правило перевода из дополнительного кода в прямой код.

Рассмотрим на примерах выполнение операции сложения двух чисел с разными знаками.

Возможны следующие случаи:

​

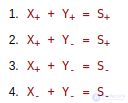
Необходимо помнить, что нельзя, выполняя операции, выходить за диапазон представляемых в данной разрядной сетке чисел, записанных сфиксированной запятой.

Положим n = 3, 1 - знаковый разряд и 2 - цифровых.

Таким образом, важной особенностью дополнительного кода является то, что знаковый разряд в процессе выполнения операции рассматривается совместно с цифровыми. Об этом говорит сайт https://intellect.icu . Возникающие переносы теряются и не влияют на результат операции.

Обратный код

Обратным называется код, для которого в знаковом разряде положительного числа пишется "0", в цифровых - модуль числа, а для отрицательного - в знаковом разряде пишется единица, в цифровых - инвертированные разряды исходного числа.

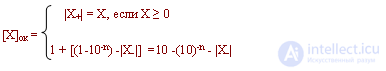
Определим диапазоны чисел:

В обратном коде есть два изображения нуля:

"Положительный" нуль:

[X]ок = 0,0...0

и "отрицательный" нуль:

[X]ок = 1,11...11

При этом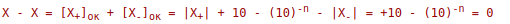

То есть, единица переноса в знаковом разряде эквивалентна единице младшего разряда. Поэтому при выполнении операции сложения-вычитания необходимо возникающий перенос циклически прибавлять в младший разряд частичного результата.

Рассмотрим прежние четыре случая, помня о том, что сумма двух слагаемых по модулю должна быть меньше единицы.

Заметим, что получение обратного кода проще, чем дополнительного. Это поразрядно выполняемая микрооперация инверсии кода. Как станет ясно из схемного решения, эта микрооперация выполняется так же быстро, как и передача кода.

Поскольку результатом операции является совокупность результатов по всем разрядам, то данную операцию можно выполнять одновременно над всеми цифровыми разрядами числа.

4. Описание преобразования чисел по стандарту IEEE 754.

4.1 Преобразование двоичного нормализованного числа в 32 битный формат IEEE 754

Основное применение в технике и программирование получили форматы 32 и 64 бита.
Например, в VB используют типы данных single (32 бита) и double (64 бита).
В Си аналогично используют float (32 бита) и double (64 бит)
Рассмотрим преобразование двоичного числа 10011011,101 в формат single-precision (32 бита) стандарта IEEE 754.
Остальные форматы представления чисел в IEEE 754 являются увеличенной копией single-precision.

Чтобы представить число в формате single-precision IEEE 754 необходимо привести его к двоичному нормализованному виду. В §3 мы проделали это преобразование над числом 155,625. Теперь рассмотрим, как двоичное нормализованное число преобразуется к 32 битному формату IEEE 754.

• Описание преобразования в 32 битный формат IEEE 754:
• Число может быть + или - .
  Поэтому отводится 1 бит для обозначения знака числа:
  0-положительное
  1-отрицательное
  Этот самый старший бит в 32 битной последовательности .
• Далее пойдут биты экспоненты, для этого выделяют 1 байт (8 бит).
  Экспонента может быть, как и число, со знаком + или -.
  Для определения знака экспоненты, чтобы не вводить еще один бит знака, добавляют смещение к экспоненте в половину байта +127(0111 1111). То есть, если наша экспоната = +7 (+111 в двоичной), то смещенная экспонента = 7+127=134. А если бы, наша экспонента была -7 , то смещенная экспонета=127-7 =120. Смещенную экспоненту записывают в отведенные 8 бит. При этом, когда нам будет нужно получить экспоненту двоичного числа, мы просто отнимем 127 от этого байта.
• Оставшиеся 23 бита отводят для мантиссы.
  Но, у нормализованной двоичной мантиссы первый бит всегда равен 1, так как число лежит в диапазоне 1<=M<2.
  Нет смыла, записывать единицу в отведенные 23 бита, поэтому в отведенные 23 бита записывают остаток от мантиссы.

В таблице представлено десятичное число 155,625 в 32-х битном формате IEEE754:

1 бит	8 бит	23 бит	IEEE 754
0	1000 0110	001 1011 1010 0000 0000 0000	431BA000 (hex)
0(dec)	134(dec)	1810432(dec)
знак числа	смещенная экспонента	остаток от мантиссы	число 155,625 в формате IEEE754

В результате десятичное число 155,625 представленное в IEEE 754 c одинарной точностью равно 431BA000 (hex).

4.2 Преобразования числа формата 32 бит IEEE 754 в десятичное число

• Чтобы записать число в стандарте IEEE 754 или восстановить его, необходимо знать три параметра:
• S- бит знака (31-й бит)
• E- смещенная экспонента (30-23 биты)
• M - остаток от мантиссы (22-0 биты)

Это целые числа которые записанные в числе IEEE 754 в двоичном виде.

Приведем формулу для получения десятичного числа из числа IEEE754 одинарной точности:

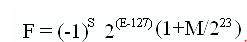где F - десятичное число

Проверяем наш пример:
F =(-1)⁰∙2^(134-127)∙(1+ 1810432 / 2²³)= 2⁷∙(1+0,2158203125)=128∙1,2158203125=155,625

Вывод этой формулы приводить не буду, все видно и так. Поясню только (1+ M/2²³) - это мантисса, единица в этой формуле- это та единица, которую мы выбросили из 23 бит, а остаток мантиссы в десятичном виде находим отношением двух целых чисел - остатка мантиссы к целому.

5. Формальное представление чисел в стандарте IEEE 754 для любого формата точности.

Рис. 1 Представление числа в формате IEEE 754

• где:
• S - бит знака, если S=0 - положительное число; S=1 - отрицательное число
• E - смещенная экспонента двоичного числа;
  exp₂ = E - (2^(b-1) - 1) - экспонента двоичного нормализованного числа с плавающей точкой
  (2^(b-1) -1) - заданное смещение экспоненты (в 32-битном ieee754 оно равно +127 см.выше)
• M - остаток мантиссы двоичного нормализованного числа с плавающей точкой

Формула вычисления десятичных чисел с плавающей точкой, из чисел представленных в стандарте IEEE754:

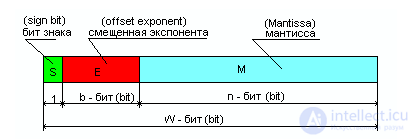
(Формула №1)

Используя формулу №1 вычислим формулы для нахождения десятичных чисел из форматов одинарной (32 бита) и двойной (64 бита) точности IEEE 754:

Рис.2 Формат числа одинарной точности (single-precision) 32 бита

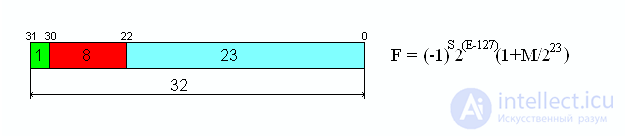
Рис.3 Формат числа двойной точности (double-precision) 64 бита

6. Представление денормализованного числа и других чисел в формате IEEE 754

• Если применить формулу №1 для вычисления минимального и максимального числа одинарной точности представленного в IEEE754, то получим следующие результаты:
• 00 00 00 00 hex= 5,87747175411144e-39 (минимальное положительное число)
• 80 00 00 00 hex=-5,87747175411144e-39 (минимальное отрицательное число)
• 7f ff ff ff hex= 6,80564693277058e+38 (максимальное положительное число)
• ff ff ff ff hex=-6,80564693277058e+38 (максимальное отрицательное число)

Отсюда видно, что невозможно представить число нуль или бесконечность в заданном формате.

Поэтому формула №1 не применяется в следующих случаях:

3. числа IEEE754=FF (1xxx)X XX XXhex не считается числами (NAN), кроме случая п.2
числа IEEE754=7F (1xxx)X XX XXhex не считается числами (NAN), кроме случая п.2
Число представленное в битах с 0...22 могут быть любым числом кроме 0 (т.е.+∞ и -∞ ).

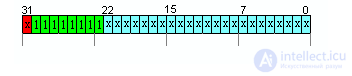
4. числа IEEE754=(x000) (0000) (0xxx)X XX XXhex считаются денормализованными числами, за исключением чисел п.1(то есть -0 и +0)

Формула расчета денормализованных чисел:

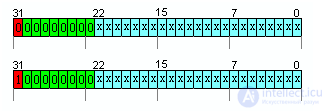
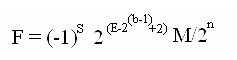(Формула №2)

• Пояснения к исключительным числам:
• С нулем понятно. Без него никак нельзя. Смущает только наличие двух нулей. Думаю, это было сделано для симметричности.
• - ∞/ +∞ , тоже понятно. Числа, которые больше границ диапазона представления чисел считаются бесконечными.
• Не числа NAN(No a Numbers). К ним относятся символы, или результаты недопустимых операций.
• Денормализованные числа. Это числа, мантиссы которых лежат в диапазоне 0.1 <= M <1.
  Денормализованные числа находятся ближе к нулю, чем нормализованные. Денормализованные числа как бы разбивают минимальный разряд нормализованного числа на некоторое подмножество. Сделано так потому, что в технической практике чаще встречаются величины близкие к нулю.

7. Сведенья по числам одинарной и двойной точности, представленным в формате IEEE 754.

7.1 Вычисление границ диапазона для чисел одинарной точности IEEE 754

Зная формат чисел с одинарной точностью стандарта IEEE 754 можно посчитать границы диапазона представления действительных чисел в этом формате. Для этого подставим значения максимальных и минимальных абсолютных чисел IEEE 754 в формулы №1 и №2.

Минимальное нормализованное число по (абсолютное)




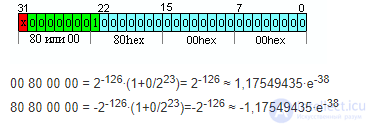
Максимальное денормализованое число (абсолютное)

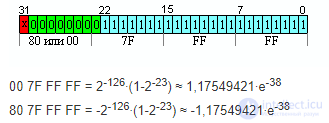
Отсюда видно что минимальное нормализированное число граничит с максимальным денормализированным.

Минимальное денормализованное число (абсолютное)

Это число граничит с нулем.

Максимальное нормализированное число (абсолютное)


Это число граничит с бесконечностью.

7.2 Полный диапазон чисел одинарной точности (32 бит) по стандарту IEEE754

Рис.4 .Диапазон чисел формата одинарной точности (32 бита) представленных по стандарту IEEE 754

7.3 Полный диапазон чисел двойной точности (64 бит) по стандарту IEEE754

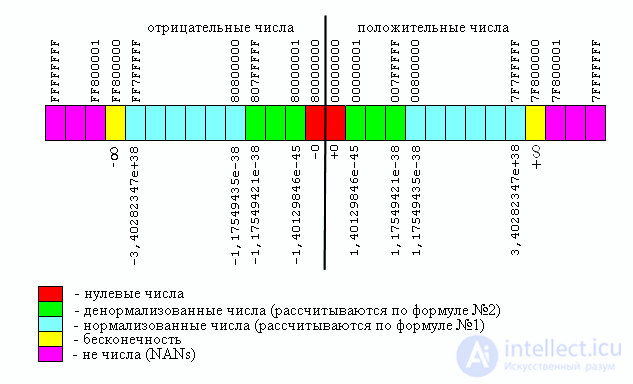
Рис.5 .Диапазон чисел формата двойной точности (64 бита) представленных по стандарту IEEE 754

7.4 Точность представления вещественных чисел в формате IEEE754.

Числа представленные в формате IEEE754 представляют конечное множество, на которое отображается бесконечное множество вещественных чисел. Поэтому исходное число может быть представлено в формате IEEE754 с ошибкой.

Рис.6 Функция ошибки точности представления числа в IEEE754

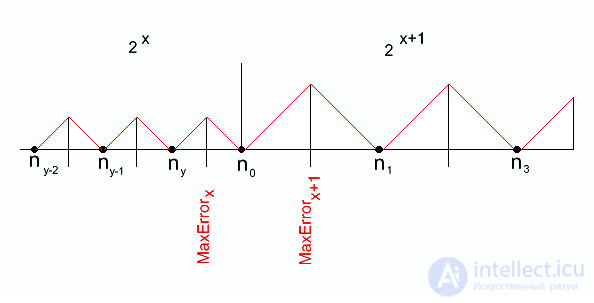
Абсолютная максимальная ошибка для числа в формате IEEE754 равна в пределе половине шага чисел. Шаг чисел удваивается с увеличением экспоненты двоичного числа на единицу. То есть, чем дальше от нуля, тем шире шаг чисел в формате IEEE754 по числовой оси.

Шаг денормализованных чисел равен 2^(E-149) (Single) и 2^(E-1074) (Double).
Соответственно предел макс. абсолютной ошибки будет равен 1/2 шага числа: 2^(E-150) (Single) и 2^(E-1075) (Double).
Относительная ошибка в % будет равна: (2^(E-150)/F)*100%(Single) и (2^(E-1075)/F)*100% (Double).

Шаг нормализованных чисел равен 2^(E-150) (Single) и 2^(E-1075) (Double).
Соответственно предел макс. абсолютной ошибки будет равен 1/2 шага числа: 2^(E-151) (Single) и 2^(E-1076) (Double).
Относительная ошибка в % будет равна: (2^(E-151)/F)*100%(Single) и (2^(E-1076)/F)*100% (Double).

Максимальная относительная ошибка для денормализованного числа(single/double):

Максимальная относительная ошибка нормализованного числа(single):

Максимальная относительная ошибка нормализованного числа(double):

Таблица 1. Максимальная возможная ошибка для чисел Single

IEEE754, hex	число, dec	абсолютная ошибка, dec	относительная, %
00000001	2-149 ≈1,401298e-45	2-150≈0,700649e-45	=50
00000002	2-148 ≈2,802597e-45	2-150≈0,700649e-45	=25
00000032	≈7,00649e-44	2-150≈0,700649e-45	=1
007FFFFF	≈1,175494e-38	2-150≈0,700649e-45	≈5,96e-6
00800001	≈1,175494e-38	2-149 ≈1,401298e-45	≈11,9209e-6
0DA24260	≈1,0e-30	2-123 ≈9,4039e-38	≈9,4039e-6
1E3CE508	≈1,0e-20	2-90 ≈8,0779e-28	≈8,0779e-6
2EDBE6FF	≈1,0e-10	2-57 ≈6,9389e-18	≈6,9389e-6
3F800000	≈1,0	2-23 ≈1,192e-7	≈11,9209e-6
41200000	≈10,0	2-20 ≈9,5367e-7	≈9,5367e-6
42C80000	≈1,0e+2	2-17 ≈7,6294e-6	≈7,62939e-6
501502F9	≈1,0e+10	210 ≈1,024e+3	≈10,24e-6
60AD78EC	≈1,0e+20	243 ≈8,7961e+12	≈8,7961e-6
7149F2CA	≈1,0e+30	276 ≈7,5558e+22	≈7,5558e-6
7F7FFFFF	≈+3,40282e+38	2104 ≈2,02824e+31	≈5,96e-6

Таблица 2. Максимальная возможная ошибка для чисел Double

IEEE754, hex	число, dec	абсолютная ошибка, dec	относительная, %
00000000 00000001	2-1074 ≈4,940656e-324	2-1075≈2,470328e-324	=50
00000000 00000002	2-1073 ≈9,881313e-324	2-1075≈2,470328e-324	=25
00000000 00000032	≈2,470328e-322	2-1075≈2,470328e-324	=1
000FFFFF FFFFFFFF	≈2,225073e-308	2-1075≈2,470328e-324	≈1,110223e-14
00100000 00000001	≈2,225074e-308	2-1074 ≈4,940656e-324	≈2,220446e-14
2B2BFF2E E48E0530	≈1,0e-100	2-385 ≈1,268971e-116	≈1,268971e-14
3FF00000 00000000	=1,0	2-52 ≈2,220446e-16	≈2,220446e-14
54B249AD 2594C37D	≈1,0e+100	2280 ≈1,942669e+84	≈1,942669e-14
6974E718 D7D7625A	≈1,0e+200	2612 ≈1,699641e+184	≈1,699641e-14
7FEFFFFF FFFFFFFF	≈1,79769e+308	2971 ≈1,99584e+292	≈1,110223e-14

Из выше приведенного следует, что основная масса чисел в формате IEEE754 имеет стабильную небольшую относительную погрешность: Максимально возможная относительная погрешность для числа Single составляет 2^-23*100% =11,920928955078125e-6 %
Максимально возможная относительная погрешность для числа Double составляет 2^-52*100% =2,2204460492503130808472633361816e-14 %

7.5 Общие сведенья для чисел одинарной и двойной точности стандарта IEEE 754.

Таблица 3. Сведенья о формате 32/64 бит в стандарте ANSI/IEEE Std 754-1985

наименование формата	single-precision	double-precision
длина числа, бит	32	64
смещенная экспонента (E), бит	8	11
остаток от мантиссы (M), бит	23	52
смещение	127	1023
двоичное денормализованое число	(-1)S∙0,M∙exp2-127 ,где M-бинарное	(-1)S∙0,M∙exp2-1023 ,где M-бинарное
двоичное нормализованое число	(-1)S∙1,M∙exp2(E-127) ,где M-бинарное	(-1)S∙1,M∙exp2(E-1023) ,где M-бинарное
десятичное денормализованное число	F =(-1)S∙2(E -126)∙ M/223	F =(-1)S∙2(E -1022)∙M/252
десятичное нормализованное число	F =(-1)S∙2(E-127)∙(1+ M/223)	F =(-1)S∙2(E-1023)∙(1+M/252)
Абс. макс. возм. погрешность числа	2(E-150)	2(E-1075)
Отн. макс. возм. погрешность денорм. числа	1/(2M)	1/(2M)
Отн. макс. возм. погрешность норм. числа	1/(224+2M)	1/(253+2M)
минимальное число	±2-149≈ ±1,40129846∙e-45	±2-1074≈ ± 4,94065646∙e-324
максимальное число	±2127∙(2-2-23) ≈ ± 3,40282347∙e+38	±21023∙(2-2-52) ≈ ± 1,79769313∙e+308

8. Округление чисел в стандарте IEEE 754.

Стандарт IEEE754 предусматривает четыре способа округления чисел.

• Способы округления чисел по стандарту IEEE 754:
• Округление стремящееся к ближайшему целому.
• Округление стремящееся к нулю.
• Округление стремящееся к +∞
• Округление стремящееся к -∞

Таблица 3. Примеры округления чисел до десятых

исходное число	к ближ. целому	к нулю	к +∞	к -∞
1,33	1,3	1,3	1,4	1,3
-1,33	-1,3	-1,3	-1,3	-1,4
1,37	1,4	1,3	1,4	1,3
-1,37	-1,4	-1,3	-1,3	-1,4
1,35	1,4	1,3	1,4	1,3
-1,35	-1,4	-1,3	-1,3	-1,4

Как происходит округление показано на примерах в таблице 3. При преобразовании чисел необходимо выбрать один из способов округления. По умолчанию это первый способ -округление к ближайшему целому. Часто в различных устройствах используют второй способ - округление к нулю. При округлении к нулю нужно просто отбросить не значащие разряды числа, поэтому этот способ самый легкий в аппаратной реализации.

9. Проблемы компьютерных вычислений, вызванные использованием стандарта IEEE754.

Стандарт IEEE 754 широко применяется в технике и программировании.
Большинство современных микропроцессоров изготовляются с аппаратной реализацией представления вещественных переменных в формате IEEE754.
Язык программирования и программист не могут изменить эту ситуацию, иного преставления вещественного числа в микропроцессоре не существует.
Когда создавали стандарт IEEE754-1985 представление вещественной переменной в виде 4 или 8 байт казалось очень большой величиной, так как объем оперативной памяти MS-DOS был равен 1 Мб. А, программа в этой системе могла использовать только 0,64 Мб. Для современных ОС размер в 8 байт является ничтожным, тем не менее переменные в большинстве микропроцессоров продолжают представлять в формате IEEE754-1985.

Рассмотрим ошибки компьютерных вычислений, вызванные применением чисел в формате IEEE754.

9.1 Ошибки связанные с точностью представления вещественных чисел в формате IEEE754. Опасная редукция.

Данная ошибка всегда присутствую в компьютерных вычислениях.
Причина ее возникновения описана в п.7.4.
Радует только то, что величина относительной ошибки имеет размерность для single 10^-6 для double 10^-14
Величины абсолютных ошибок могут быть значительными, максимально для single 10³¹ и для double 10²⁹², что может вызывать определенные проблемы вычислений.

Если пример посчитать на бумажке, то ответ будет 1. Абсолютная ошибка равна +7.
Почему ответ получился неправильным?
Число 123456789 в single=4CEB79A3hex(ieee)=123456792(dec) абсолютная ошибка представления равна +3
Число 123456788 в single=4CEB79A2hex(ieee)=123456784(dec) абсолютная ошибка представления равна -4
Относительная погрешность исходных чисел приблизительно равна 3,24e-6%
В результате одной операции относительная погрешность результата стала 800%, т.е. увеличилась в 2,5e+8 раз.
Это я называю "Опасной редукцией", т.е. катастрофическим понижением точности вычислений в операция где абсолютное значение результата много меньше любого из входного значения переменных.

На самом деле ошибки точности представления числа наиболее безобидные в компьютерных вычислениях, и обычно многие программисты на них не обращают никакого внимания. Тем не менее они вас могут сильно огорчить.

9.2 Ошибки связанные с неправильным приведением типов данных. Дикие ошибки.

Эти ошибки вызваны тем, что исходное число представленное в формате single и в формате double обычно не равны друг другу

.

Вот пример на VB:

Относительная погрешность результата равна: ∞ (бесконечности)
Такую ошибку называют "грязным нулем".
Если переменные привести к одному типу, то этой ошибки не будет.

Поэтому переменные и промежуточные результаты компьютерных вычислений должны быть приведены к одному типу данных.
Например, требование приведения данных к одному типу изложено в стандарте на язык Си ISO/IEC 9899:1999.

Обратите внимание на то, что недостаточно просто привести все исходные данные к одному типу. Необходимо привести также результаты промежуточных операций к одному типу.
Вот пример с ошибкой в промежуточном результате:

Здесь ошибка возникает потому, что промежуточный результат 1/3 в строке c=c-1/3 будет иметь тип double, а не single. Чтобы избавиться от ошибки вам надо привести промежуточный результат к типу single с помощью оператора приведения типов CSng.

Пример приведения типа данных для GNU C :

Во втором варианте вы видите, что деление констант в промежуточном результате приведено к типу "float" (одиночная точность в Си). Данные варианты компилировались и исполнялись с помощью "GNU C".
Если компилировать и исполнить показанные выше варианты на VC++ (Visual Studio), то результаты будут обратными. То есть вариант 2 будет иметь результат -9.934108, а вариант 1 Result: 0.000000.
Отсюда можно сделать неутешительный вывод, что результат вычислений может зависеть от типа и версии компилятора. В данном случае можно предположить, что компилятор VC++ автоматически приводит типы переменных, и попытка их насильственного приведения к одному типу заканчивается ошибкой.

Если Вариант 1 (без приведения типов) выполнить с переменными двойной точности (double), то ошибки приведения данных не будет и Result=0.000000
Поэтому в большинстве случаев чтобы избавиться от приведения типов данных надо просто использовать тип данных double и забыть о существовании типа single(float).
Ошибки вычислений вызванные не приведением типов данных я называю "Дикими ошибками", так как они связаны с незнанием стандартов и теории программирования (т.е. с плохим фундаментальным образованием)

9.3 Ошибки вызванные сдвигом мантисс. Циклические дыры.

Эти ошибки связаны с потерей точности результата при неполном пересечении мантисс чисел на числовой оси.
Если мантиссы чисел не пересекаются на числовой оси, то операции сложения и вычитания между этими числами невозможны.
К примеру возьмем число Single: 47FFFFFF = +131071,9921875(dec)
В двоичной системе это число выглядит так: +11111111111111111,1111111

Покажем несколько компьютерных операций сложений и этим числом в формате Single
Значащих цифр в мантиссе двоичного числа в формате Single не более 24
Красным цветом показаны цифры выходящие за этот предел и не участвующие в формате Single

1. сложение с одинаковым числом (ошибка сдвига =0.0).

2. сложение с числом меньшим в 2 раза (ошибка сдвига= - 0.00390625).

3. сложение с числом меньшим в 2²³ раза (ошибка сдвига= - 0.007812).

4. сложение с числом меньшим в 2²⁴ раза (ошибка сдвига= - 0.007812).

В последнем примере мантиссы чисел разошлись, и арифметические операции с этими числами становятся бессмысленными.

Как видно из приведенных примеров ошибка сдвига возникает если у исходных нормализованных чисел различаются экспоненты. Если числа отличаются более чем в 2²³ (для single) и 2⁵² (для double), то операции сложения и вычитания между этими числами не возможны.
Максимальная относительная погрешность результата операции равна примерно 5,96e-6%, что не превышает относительную погрешность представления числа (см.п.9.1).

Хотя с относительной погрешностью здесь все в порядке, здесь есть другие проблемы.
Во-первых, работать с числами можно только в узком диапазоне числовой оси, где мантиссы пересекаются.
Во-вторых, для каждого исходного числа существует предел выполнения цикла называемый "Циклической дырой". Поясню, если существует цикл в котором исходное число суммируется к сумме, то существует численный предел суммы для этого числа. То есть сумма достигнув определенной величины перестает увеличиваться от сложения ее с исходным числом.

Приведу пример циклической дыры в автоматической системе управления:
Имеется фармацевтический цех, производящий таблетки весом 10мг.
Состоящий из: формовочной машины, накопительного бункера на 500 кг, фасовочной машины, автоматической системы управления.
Формовочная машина подает в бункер по 10 таблеток одновременно. Фасовочная машина забирает по одной таблетке.
Автоматическая система управления учитывает таблетки поступившие в бункер от формовочной машины и взятые из бункера фасовочной машиной. То есть существует программа, которая показывает заполнения бункера продукцией в кг. Когда в бункере будет более 500 кг продукции, формовочная машина встает на паузу , она включиться кода в бункере станет 200 кг продукции. Фасовочная машина остановиться если в бункере будет менее 10 кг и запустится когда в бункере будет более 100 кг продукции.
Обе машины могут периодически останавливаться для обслуживания , не зависимо друг от другу (благодаря бункеру).

Как вы понимаете, такая система работает в бесконечном цикле.
Допустим в один из дней фасовочная машина простояла слишком долго и бункер заполнился до 300 кг.
Что произойдет после ее включения?

Упрощенный пример работы цикла программы управления:

В данном примере фасовочная машина забрала из бункера 100 кг продукции, а вес продукции в бункере не изменился.
Почему не изменился?
Потому, что мантиссы чисел 300 и 0,00001 не пересекаются для формата single.

Далее формовочная машина доведет вес бункера до 500 кг и остановится. Фасовочная машина заберет все таблетки из бункера и тоже остановится. Программа будет показывать вес в бункере 500кг. Прибегут специалисты, проверят датчики, провода, компьютер и скажут что программа зависла. Но, программа не зависала, она продолжает работать без сбоев и любой контроль это подтвердит. Просто число 0,0001 попало в циклическую дыру и выйти из него не может.

В результате нам крупно повезло, что это был фармацевтический цех, а не Саяно-Шушенская ГЭС.

На самом деле опытный программист никогда не будет делать циклическое вычитание(или суммирование) таким образом. Этот пример вымышлен специально, и так считать нельзя, хотя с точки зрения математика здесь все безупречно. Эта ошибка свойственна математикам и начинающим программистам.
Я бы сказал, что основная работа программиста заключается в борьбе с погрешностями, а не в математических решениях поставленной задачи.

Привожу правильный пример решения этой задачи, любезно предоставленный Ситкаревым Григорием:

Показанный выше пример взят из реального промышленного кода.
Для наглядности упростим выше приведенный пример.

Как видно из этого примера, программисту приходится вычислять погрешность результата в каждом цикле, чтобы учесть ее в следующем цикле.
Обратите внимание, что программист должен быть абсолютно готов к тому, что некоторые основные понятия математики могут не выполняться при вычислениях в формате IEEE754. Например, правила алгебраической коммутативности (a + b) + с = (a + c) + b, обычно не выполняются при таких вычислениях.
К сожалению, в современном фундаментальном математическом образовании этому вопросу уделяют мало внимания, оставляя решения проблем инструментария на прикладного программиста.

9.4 Ошибки вызванные округлением. Грязный ноль.

При компьютерных вычислениях можно выделить два вида округления:
1. Результат выполненной арифметической операции всегда округляется.
2. Вывод и ввод вещественного числа в окно Windows происходит с округлением.

В первом случае переменная округляется по одному из 4-типов округления IEEE754, по умолчанию округление происходит к ближайшему целому.
При этом переменная принимает новое округленное значение.
В п.9.2 мы рассматривали сложение двух одинаковых чисел:

1. сложение с одинаковым числом (ошибка сдвига =0.0).

Здесь результат операции сложения двух чисел абсолютно точен, но результат был округлен микропроцессором. Таким образом к точному результату была добавлена ошибка округления. В общем случае ошибка округления находится в пределах точности числа.

Во втором случае переменная не меняет своего значения, просто в окно Windows выводится округленное значение вещественного числа. Получается, что исходная переменная и ее отображение в окне Windows это разные числа. Это не ошибка формата IEEE754, это ошибка Windows.
Для переменных типа Single в окне Windows отображается 7 значащих цифр округленных до ближайшего целого.
3DFCD6EA =+0,12345679104328155517578125 в окне отображается как 0,1234568
Для переменных типа Double в окне Windows отображается 15 значащих цифр округленных до ближайшего целого.
3FBF9ADD3746F67D=+0,12345678901234609370352046653351862914860248565673828125 отображается как 0,123456789012346

Вопрос какое значение имеет переменная когда мы вводим в окно Windows 0,123456789012346 ?
Это значение будет равно такому числу:
3FBF9ADD3746F676=+0,1234567890123459965590058118323213420808315277099609375
То есть значение переменной 3FBF9ADD3746F67D мы вообще не можем вставить напрямую в код программы.
Но, мы можем схитрить и вставить в программу x=0.123456789012346 +1E-16. Полученная переменная будет равна 3FBF9ADD3746F67D (это используется в примере с грязным нулем)
Отобразить или вести через окно ПК такое число невозможно.

В результате действий Windows возникает ряд неприятных ситуаций.
1. У вас нет технической возможности отображать или вводить точные значения переменных в окнах, что само по себе очень печально.
2. Возникновение серьезных ошибок, таких как грязный ноль.
"Грязный ноль" это когда вы или программа считаете, что переменная не равная нулю - равна нулю

Очень часто эта ошибка возникает в интерфейсе "оператор-машина".
Например, при обнулении тары в весовых программах.

Dim a As Double
	'обнуление видимой величины
Private Sub Command1_Click()
    		Dim b As Double
    		Dim c As Double
  
    		b = Val(Replace(Text2.Text, ",", "."))
    		c = a - b
   		 Text3.Text = c
End Sub

Private Sub Form_Load()
		'ввод числа 3FBF9ADD3746F67D 
     		a = 0.123456789012346 + 1E-16
    		Text1.Text = a
End Sub

Результат выполнения программы приведенного выше примера

В результате переменную, которую оператор считает нулем - нулю не равна
Относительная погрешность результата равна бесконечности.
В логических операциях сравнения этот не ноль может увести исполнение программы в другую ветвь алгоритма.

10. Арифметические действия над числами с плавающей точкой

• Сложение
• Умножение
• Деление

10.1 Сложение чисел с плавающей точкой

1. Уравнивание порядков
2. Сложение мантисс в одном из модифицированных кодов
3. Нормализация результата

Пример.
Представить числа в виде нормализованных двоичных чисел с плавающей точкой и сложить.

10.2 Умножение чисел с плавающей точкой

1. Умножение мантисс в прямом коде.
2. Сложение порядков.
3. Определение знака числа (логическая операция исключающее или)

Пример.
Представить числа 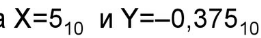в виде нормализованных двоичных чисел с плавающей точкой и перемножить.

10.3 Деление чисел с плавающей точкой

Пример.
Представить числа 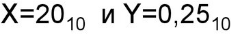в виде нормализованных двоичных чисел с плавающей точкой и вычислить X / Y.

Выводы из данной статьи про способы представления чисел в эвм указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое способы представления чисел в эвм и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровые устройства. Микропроцессоры и микроконтроллеры. принципы работы ЭВМ